AN EFFECTIVE DETAILED ROUTING ALGORITHM CONSIDERING ADVANCED TECHNOLOGY NODES∗

Xiqiong Bai, Dixiu Xiao, Jianli Chen, Wenxing Zhu,Yadong Zhang, Taotao Lu, Lifeng Wu

(1. College of Mathematics and Computer Science, Fuzhou University,Fuzhou 350116, Fujian, PR China;2. Center for Discrete Mathematics and Theoretical Computer Science,Fuzhou University, Fuzhou 350116, Fujian, PR China;3. Empyrean Software, Inc., Beijing 100000, PR China)

Abstract Detailed routing has become much challenging in modern circuit designs due to the extreme scaling of chip size and the complicated design rules. In this paper,we give an effective algorithm for detailed routing considering advanced technology nodes. First, we present a valid pin-access candidates generation technology for handling complex pin shapes. Then, we propose a tree-based nets components selection algorithm to decide connecting order for multiple nets components. Finally, combined with global routing results and advanced technology nodes,an initial routing results optimization algorithm is presented to achieve the final detailed routing results. Experimental results on industry benchmarks show that, our proposed algorithm not only achieves 100%routability on real industrial cases in a reasonable runtime, but also optimizes total wirelength, total vias and other advanced technology nodes simultaneously.

Keywords detailed routing;advanced technology nodes;pin-access;total vias

1 Introduction

Routing is considered as the most time-consuming and important stage in the VLSI design flow. In addition, with ever increasing requirements, many new design rules are introduced to satisfy modern industrial demands. Due to the complexity of the routing problem,routing is usually divided into two stages: global routing and detailed routing. During the global routing stage, nets are routed on a coarse-grain grid structure with the objective of determining the regions within which each net will be routed. After an approximate routing solution is determined for each net,the detailed routing stage is to find the exact routes of all nets [1]. Since detailed routing is generated based on the global routes,the quality of the final interconnects depends largely on the quality of the global routing solution [27].

Considering advanced technology nodes in detailed routing is a complicated step in the physical design process. A high-performance chip requires that several corresponding metrics need to be evaluated and considered in this dead-or-alive process.With the aim to achieve a better detailed routing result, honoring global routing results can maximize reducing the disturbance to these metrics(e.g.,timing,routability [3], manufacturability, skew, and congestion [2,15,16]), and so on. Figure 1 is a comparison of routing results of whether or not to take into account the impact of congestion for a net with four pins. If the detailed router routes wires over the region as shown in Figure 1 (a), it will have overlapped wires because of congestion.Figure 1 (b) is a modified detailed routing result considering advanced technology nodes. With the rapid development of modern industrial tools and lithography requirements, satisfying all advanced technology nodes in a detailed routing process is becoming more and more challenging. Therefore, several corresponding metrics need to be managed in different steps during the detailed routing process to meet all constraints in the final detailed routing result.

1.1 Previous work

Many works have been presented for VLSI routing based on the shortest path algorithms, which can be divided into two categories: maze routing algorithm and line-search algorithm [4,5]. The fundamental maze algorithm isLee’salgorithm [6],which is an application of the breadth-first search method. This algorithm consists of two main phases,and is applied to a uniform grid with known starting and ending points of a net. In the first phase,adjacent points of the starting point of the net are marked by label 1. Then after each stepi, the unmarked neighbors of the labeled elements are labelled byi+1. This phase will be repeated until the target point is found. The shortest path is produced by backtracking diminishing labels from the target point to the beginning point in the second phase. If there exist several neighboring points with the same label, the guidance for choosing the next point is to follow the path’s direction and decrease the number of bends at the same time.

After that,by applying the A*heuristic search,Hadlock[22]proposed a shortest path algorithm called the Minimum Detour(MD)algorithm, which is guided by the number of detours during the path search process. Compared toLee'salgorithm,the MD algorithm not only costs less time and the number of detours during the shortest path stage, but also achieves a better result. Different from the MD algorithm, Soukup’s algorithm [8] combined advantages of the depth-first search and the breadth-first search, which improves the runtime of the original maze-routing algorithm. However, since it is a heuristic search method, the path found is usually not the shortest.

The search lengths at each step of all the above maze-routing algorithms are unit grid length, which adds the burden of storage and search ability during the routing process. As a result, line-search algorithms have been proposed to change this situation. The search segments are series of effective lines rather than unit grid intervals. Hence they can save runtime and memory for finding a single-shaped path, but usually cannot ensure to find a shortest path. For example,Hetzal'salgorithm[9]is an improved A*algorithm which searches intervals instead of nodes.Intervals are generated by clustering one row or one column of consecutive identical cost nodes, and are stored before the path searching process. However,Hetzal'salgorithm was proved that it does not enhance the running time [10]. What’s more,these algorithms are mainly used for graph grids and the corresponding solution may be limited. So they cannot meet our research requirements for detailed routing with advanced technology nodes.

In addition, the above mentioned algorithms are mainly the path search process between two points. However, routing terminals of a net may not be a single source and a target,and the characteristics of multi-terminal nets indicate that our routing problem is an NP-complete problem [11]. Hence, basic methods of the Steiner tree problem have been widely promoted to minimize the total wirelength and consider other constraints. Typical approach to route a multi-terminal net is usually divided into two steps, that is, build a Steiner tree firstly, and then search a path between two points based on all pairs of connections of the tree.

Many routing methods have been proposed to solve the multi-terminal net routing problem,which includes two main types of algorithms: sequential and concurrent routing algorithms. Sequential routing algorithm has the advantage of simpleness,but routing one net may affect routability of other nets or degrade routing quality of all nets. To avoid this issue, another kind of algorithms attempt to find the final results of all nets concurrently. Shragowitz [12] proposed an algorithm based on the multicommodity flow formulation for two-terminal nets. Raghavan[13]presented an improved algorithm which can handle three-terminal nets. Later, Albrecht[14]gave a rigorous algorithm for global routing based on a new approximation algorithm for the multi-commodity flow problem.

In VLSI detailed routing, the solution space is much smaller than that of global routing. Since it is rather hard for an optimization method to consider global routing and advanced technology nodes simultaneously, it is great to design efficient detailed routing algorithms for producing high quality routing solution with considering advanced technology nodes.

1.2 Our work

In this paper, we design an effective algorithm flow to achieve a detailed routing result with global routing information and advanced technology nodes. Based on the circuit netlist and global routing results information, our algorithm connects all nets efficiently and optimizes the total wirelength,the total number of vias,the outof-rectangle vias and wirelength, wrong wires and off-track vias. In our algorithm,we identify shape-based pin-access candidates by considering spacing violation and remaining enough available routing space. After preprocessing of all valid points for nets, tree-shape structure is used to select sequence of connections for optimized nets with the aim to decrease our routing area and wirelength. Finally, we propose an optimized detailed routing process by considering global routing information and advanced technology nodes. The main contributions of our work are summarized as follows:

•A valid pin-access candidates generation algorithm is proposed to obtain valid pin-access candidates from different shape of pins within track grids. Since some connection violations may have a large effect on later detailed routing stage, after generating pin-access candidates, spacing violation-aware candidates restriction is applied to achieve valid pin-access candidates.

•A tree-based nets components selection algorithm is applied to select net’s components points by reducing total wirelength and total vias. We first divide nets multiple components into several pairs with corresponding weights, then establish connection points of these components based on known division.This algorithm can reduce abstract distance between two points for each pair of components, and decrease the total wirelength and total vias for the whole net.

•An algorithm is designed for optimizing initial routing results. Initial detailed routing solution is produced by carrying out a rectangle-driven A* algorithm at first,then based on via candidates,detailed routing optimization is presented to honor global routing results and consider advanced technology nodes for the whole net, with the aim to reduce out-of-rectangle wirelength, number of vias and other constraints.

•Experimental results show that our algorithm can achieve 100%routability in a reasonable runtime, while handling several advanced technology nodes with optimized total wirelength and total vias on industrial benchmarks.

The rest of this paper is organized as follows. Section 2 is the preliminaries.Section 3 describes our algorithm in detail for our complicated detailed routing problem. Empirical studies of our proposed algorithm are presented in Section 4.Finally, conclusion is given in Section 5.

2 Preliminaries

2.1 Modern connection constraints

In this subsection,several modern connection constraints and routing preference metrics will be described for satisfying the industrial advanced technology nodes on global routing results.

1)Open Net.The pins of each net need to be fully connected. If any pin in a net is disconnected, the net will be considered as an open net, and our detailed router will regard this kind of nets as failed wires.

2)Cut Spacing.The cut spacing specifies the minimum spacing distance between every two vias on cut layers, which ensures that vias on the same net or different nets must be placed satisfying the minimum spacing distance.

3)Min Area.By specifying the min area rule for all routing segments, the area of each routing polygon must be equal to or bigger than the default minimum value. Apatchmay be added to the polygon in order to increase its area up to the minimum default value.

4)Short Area.In our industrial benchmarks, each metal layer has only one value of width. Namely, a short area violation will happen when either a via or metal wire overlaps with another via model, metal wire, blockages, or pin shapes.These cases can change the stable width value, and all intersection part of these cases are the short area.

5)Rectangle Spacing.All rectangles on routing layers have a default minimum spacing value between every two objects, such as the spacing between two routing segments, the spacing between wires and obstacles, the spacing between vias and obstacles, and so on.

An example of detailed routing result which violates connection constraints is presented in Figure 2. These situations indicate that every routing segment needs to satisfy specific connection constraints by considering advanced technology nodes during the detailed routing process.

2.2 Routing preference metrics

Due to modern connection constraints and other limited routing resources, we use several routing preference metrics [17] to evaluate the detailed routing quality, such as out-of-rectangle wirelength and vias, wrong-way routing and off-track routing. The distinction between routing preference metrics and modern connection constraints is the influence on routing results. By optimizing these metrics during the detailed routing process we can improve the quality of detailed routing results.We describe these metrics in detail in the following concepts.

1)Out-of-Rectangle Wirelength and Vias.Following global routing results is a wise choice for detailed routing process. Since global routing results in our industrial benchmarks are lists of rectangles which are saved in a specific file, each list of rectangles of one net can ensure to cover a detailed routing solution of the associated net. However, due to the congestion location of pins and limited global routing space, out-of-rectangle wires and vias are acceptable to accomplish all routing nets while considering other connection constraints.

2)Wrong-Way Routing.All routing layers have a preferred routing direction,which is either horizontal or vertical to guide routing path on the corresponding metal layer. What’s more,routing directions on adjacent metal layers must be mutually perpendicular to each other to satisfy modern chip structure. If a horizontal wire exists on a vertical metal layer, this horizontal wire is called a wrong-way wire.Wrong-way wires may lead to a bad final routing result.

3)Off-Track Routing.Each metal layer has its track grids for assigning routing resources within a given wiring range. This means off-track routing wires are not aligned with track grids, and vias located outside the given track grids are off-track vias. Since the via structure is made up of two adjacent metal layers and a cut layer,routing wires on different layers needs to abide by specific tracks grids of different layers at the same time.

2.3 Problem statement

Given a set ofmnetsN={n1,n2,··· ,nm}, each net has its specific pin information, and a set ofmglobal routing resultsG={g1,g2,··· ,gm}, which are comprised by several rectangles. The goal of our detailed routing problem is to achieve a routing result for each netni ∈Nwhile considering its corresponding global routing resultgi ∈G,and each net also should optimize the following metrics simultaneously: (1) all nets need to guarantee no open nets or short areas in our detailed routing results; (2) the total wirelength of all nets; (3) the total number of vias; (4) the out-of-rectangle vias and wirelength; (5) wrong wires and off-track vias.

In this paper, our detailed routing problem is based on the 3-D grid graph structure with unit length of grid per layer. Assume that the preferred direction of metal 1 is horizontal, and adjacent metal directions are perpendicular to each other. Our routing capacity of the unit track grids is only those unblocked edges with corresponding routing preference direction.

All benchmarks are derived from a single-core 32-bit processor with four memory cores, and multi-terminal nets are included without power and ground (PG) nets.Complex pin shapes exist not only in a single metal layer,but also in multiple metal layers. What’s more, the number of blockages and layers, the die area of routing have increased the difficulty of our routing problem. The complicated industrial benchmarks indicate that line-search algorithms may not be applied to our problem,since they have designated routing direction and cannot route all nets successfully.

3 Our Algorithm

The overall flow of our algorithm is summarized in Figure 3. It starts with preprocessing circuit netlist and global routing results information on track grids. Circuit netlist is made up of specific pin information of all nets, and every pin information is decided by its relative orientation and location on corresponding boxes. A list of rectangles with assigned layers represents the regions passed by the global routing result of the associated net, which guarantees to cover at least a fully connected detailed routing solution for the net. After completing the above processes, our routing resources are divided into several kinds of points and our algorithm consists of three main parts: (1) valid pin-access candidates generation, (2) tree-based nets components points selection, (3) optimizing initial routing results. We will detail these three major parts in the following subsections.

3.1 Valid pin-access candidates generation

In this subsection,to reduce the complexity of this process,we define the concepts of pin-access candidate and valid pin-access candidate [18,19] as follows.

1)Pin-Access Candidate:A pin-access candidate on a metal layer is the intersection point of every two adjacent track grids within corresponding pin shapes.Pin-access candidates on the same single layer are put into a vertex set,and through this step, multiple sets of vertices corresponding to different layers are generated for the entire chip. In our pin-access candidates generation step, two pin shapes never share the same pin-access candidate, but one pin shape may have many pin-access candidates.

2)Valid Pin-Access Candidate:A pin-access candidate is valid if we can place at least one type of vias at that point without violating some connection constraints, such as spacing distance between vias and other objects. Otherwise,these pin-access candidates are considered invalid.

We intend to achieve valid pin-access candidatesPvcfor each net with their global routing information and spacing constraints. Since the off-track wires and wrong wires may have a negative effect on routing result, we firstly present a technology to build track grid with routing direction for each layer. Specifically, a track gridTgfor a metal layer is created uniformly which covers the entire design area from bottom to top (or left to right). Secondly, all pin access candidatesPcare created by the intersection of points in pin shapes of every two adjacent track grids.

After creating pin-access candidates by track grids and pin information, we use Algorithm 1 to select valid pin-access candidates. Based on the generated vertex sets of pin informationPiand preprocessed track gridsTg, we generate pin-access candidates for every pin at the beginning, then inspect set of vertexesPciwith spacing constraints. All candidates violating spacing constraints are saved inPvsfor later judgment. If no points are created within track grids, then a unit track interval is added to expand our search scope each time. We takeTuin pseudo code to count the number of expansions. After shape-based pin-access candidates are created, these candidatesPvsviolating spacing constraints are removed.

Algorithm 1: Valid Pin-Access Points Require: Pi,Tg,Pvs Ensure: Pvc 1: Tu ←0,pvc(used) ←0,Pvc ←0;2: while Pi is not empty 3: for every pin in Pi 4: Pc ←Get pin access candidates;5: for every Pci ∈Pc 6: if Pci ∈Pvc(used) or Pci ∈Pvs 7: Pvc ←PcPci;8: Pvc(used) ←Pvc(used)∪Pci;9: Tu ←Tu+1;10: end if 11: end for 12: end for 13: end while 14: return Pvc

Figure 4 is an example to find valid pin-access candidates considering specific spacing rules. Since two generated pin-access candidates in Figure 4 (a) cannot satisfy the spacing constraint, a unit track interval is expanded in Figure 4 (b) on the second point to produce our valid pin-access candidates, in which the purple point is our valid pin access point for this pin.

Figure 4: An example to find valid pin-access points

In addition, if the density of obstacles on the first metal layer is high, we may prefer to route less nets on this layer for routability of later process. Thus, if valid pin-access candidates are located in the range of global routing results, a via can be directly generated to start routing on the upper metal. Otherwise, we need to choose valid pin-access candidates closest to the global routing results and to find the shortest path to connect them on the first metal layer.

3.2 Tree-based net’s components points selection

Components of a net are pins of this net. After the first step for finding valid pin-access candidates, the second step is to select a point of each pin for each net by optimizing total wirelengthLtotaland the total number of viasVtotal.

3.2.1 Net’s components division

With a set ofnpins on a net, a graphG(V,E) is constructed to divide each net into tree shape. Vertexes of the graph are composed of net components, and every two vertexes has an edge between them. Owing to the complexity of pin shapes, we set coordinates of all vertexes as the center points of the rectangles. With the aim to reduce total wirelength and total vias, connecting two far vertexes and searching random directions are meaningless.

Our connecting order of these vertexes starts from choosing the leftmost candidate of all nets, then Prim algorithm is applied to construct the minimum spanning tree (MST) on the above graph for each net, which aims to search for a minimum spanning tree within the weighted connected graph. The tree formed by the edge subset includes not only all the vertices in the connected graph, but also the sum of the weights of all the edges is the smallest.

In our algorithm, the weight for each edge is the Manhattan distance between two vertexes and the via number calculated from the global routing results. We define the weight of a via as 5, and the weight of Manhattan distance of an edge between two points is 1. Then, the edge weight is

With the above graphG(V,E), we choose a root nodex ∈V(the leftmost point)and generate a minimum spanning tree.

3.2.2 Division-aware components points establishment

Since our net’s connecting order are derived from the generated spanning tree,the following step is to effectively extract connection points of every pin of a net.A bipartite graph is used to select net’s components points. Each pin shape has one or more valid pin-access candidates, and since too close pin-access points may have space violation, retaining access points for other pins as more as possible is a better choice. So we construct the grid graph as a bipartite graph according to the generated spanning tree. Vertexes in the bipartite graph are two disjoint sets, and weighted edges represent the cost of connecting these two points. We select an edge with the minimum weight in the bipartite graph.

Figure 5 (a) shows that our net componentP1has five valid pin-access candidates, and another net componentP2has four valid pin-access candidates. So 20 possible connections and associated weights are generated in this bipartite graph.The selected edge is labeled purple in Figure 5 (b).

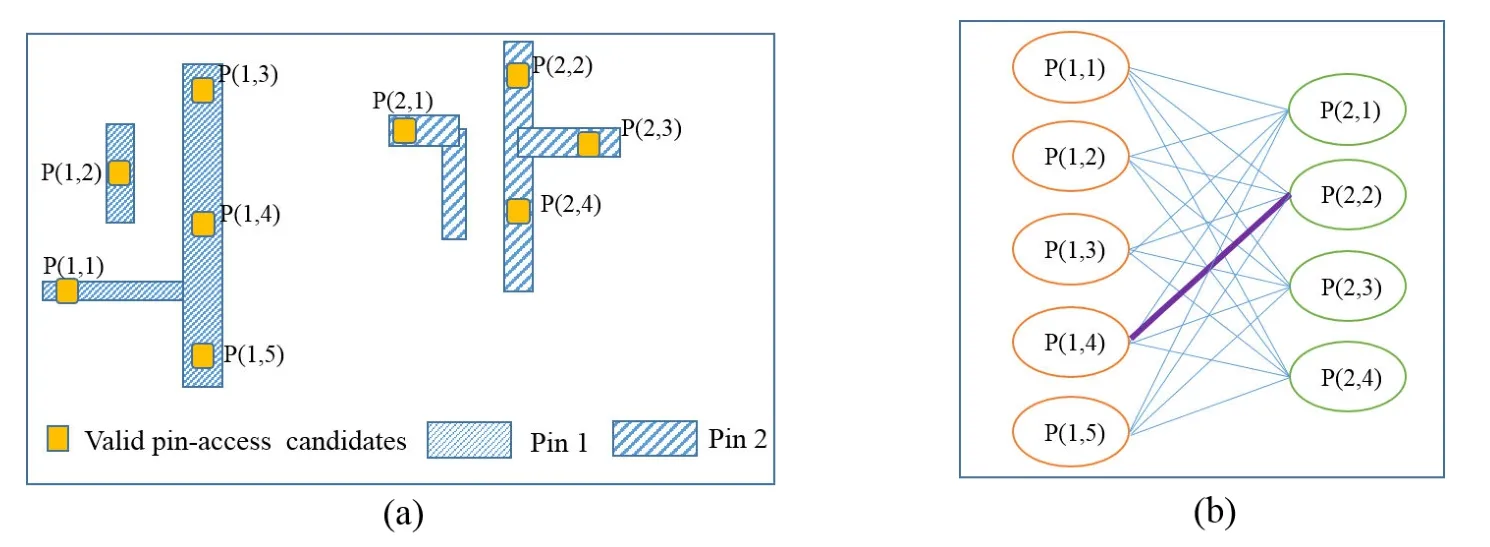
Figure 5: An example to establish net’s components connection points

3.3 Optimizing initial routing result

In this subsection, our process is split into two stages to achieve our detailed routing results.

3.3.1 Rectangle-driven initial routing solution

For every edge established in Section 3.2.2, we use A* algorithm to build an initial routing scheme, in which the cost function is the sum of the distance between the current search point and start point and the distance between the current search point and target point. In this routing scheme for an edge, the routing preference metrics may be bad. To improve the metrics, we use the following method to adapt the initial routing.

First, we set up a conflict graphG=(V,E). All initial routing segments of nets on the same metal layer are regarded as vertexes, and each edgeindicates that two segmentson the same metal layer overlap with each other.Let the weightof vertexbe the sum of track length without wrong-way routing and off-track routing. To achieve segments with better routing preference metrics, we solve the following problem by using Branch-and-Bound solver to select segments with respect to vertexes of the conflict graph:

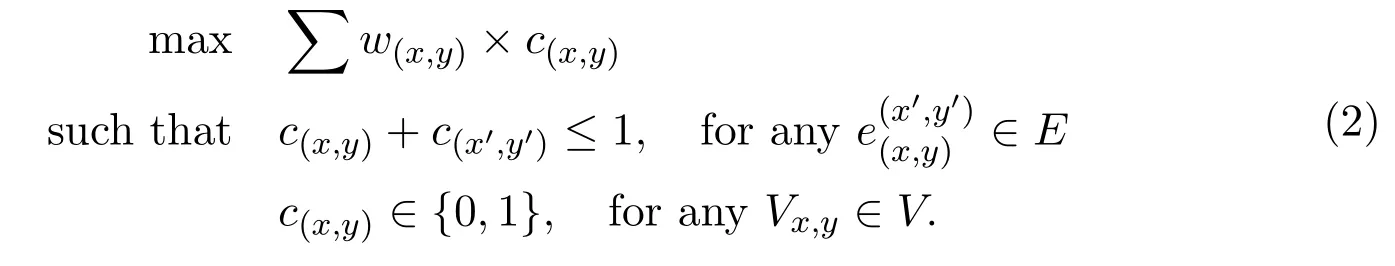
In the above formulation,c(x,y)is a binary indicator of deciding whetherVx,yis used in the following rerouting stage. The aim of rerouting is to achieve routing segments with improved routing preference metrics. We iteratively rip-up segments with respect to vertexes until there are no conflict edges in the graph.

3.3.2 Initial detailed routing solution optimization

After accomplishing detailed routing with respect to routing preference metrics,we further optimize the detailed routing solution honoring the global routing results as much as possible, and reroute segments overlapped or violating connection constraints. In this stage, our initial detailed routing results are divided into routing segmentsRiby via locations. This step can efficiently simplify our method to deal with modern advanced technology nodes.

First, we find open nets and short areas according to modern connection constraints on our track grids. Then for each routing layer, we define a panelLito be thei-th metal layer, andRito be the set of all routing segments on thei-th metal layer. LetSCostbe the overlapped wirelength of a segment, andOCostbe a binary variable to indicate whether or not this segment is open.

We preprocess all nets according to spacing rules described in modern advanced technology nodes before our detailed routing process [23,26]. For any via, routing segment and other object of routed nets, we label the rectangle centered at the via,routing segment or other object with width of the minimum spacing as a blockage during the next routing process. This step can satisfy the minimum distance constraint between any two of vias, other objects and segments for the next routing process. By the way,CCostis set as a binary indicator, which indicates if a segment satisfies the spacing constraint or not.

Minimum area rule specifies that all routing segments in our results should be larger than minimum manufacturable size. In order to satisfy this constraint, we need to insert patch for those segments violating the minimum area rule. LetMCostbe a binary variable indicating whether or not to add patch to a segment.

Due to the particularity of our global routing results and complicated pin information, we need to consider out-of-rectangle wirelength (Loc), wrong wires (Lwl),out-of-rectangle vias (Voc) and off-track vias (Vot) metrics in our detailed routing process. Compared with previous connection constraints, these metrics have less influence on our detailed routing results, but are still considered in our cost for optimization.

All the above metrics need to be optimized together for every panel. Therefore,a weighted sum of these costs is generated below to assess our routing results. In equation(3),the coefficients ofOCost,SCostandCCostreveal that these metrics have a higher priority to optimize:

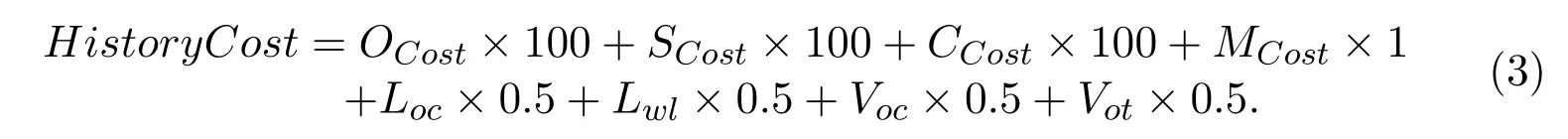
In Algorithm 2, we detail the process of reducing history cost of one segment in a panel. It must be noted that, our previous history costs of segments in one panel need to be updated after each iteration. This step will be continued until no segments have any violation of advanced technology nodes.

Algorithm 2: Overall Reduction of Violation of Constraints for a Panel Require: Panel Li, routing segments Ri 1: for the j-th routing segment Rij ∈Ri 2: calculate History Cost of Rij;3: repeat 4: Hmax = selectMaxCostsegmentRij;5: rip −up Hmax;6: reroute segment Rij;7: update History Cost of Rij;8: until termination condition is satisfied;9: end for 10: return Ri

4 Empirical Studies

In this section, we implement our detailed routing algorithm in the C++ programming language, and test it on modern real industrial benchmarks. All features of each modern industrial benchmark are described in Table 1.

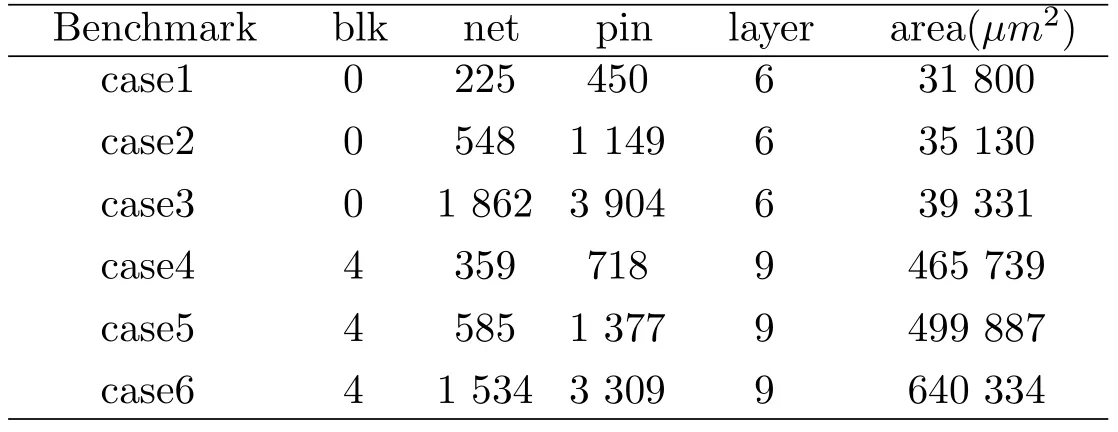
Table 1: Characteristics of modern industrial benchmarks

There are two kinds of benchmarks. The first kind contains three industrial benchmarks without blockages and vast majority of nets are with two terminals.The second kind of industrial benchmarks is with blockages, the range of routing area, routing layers numbers, and there are a large number of multi-terminals nets.All benchmarks are derived from a single-core 32-bit processor with four memory cores with modern manufacturing design rules. Table 1 presents the exhaustive statistics information of our modern industrial benchmarks, where “blk”, “net”,“pin”, “layer”, “area” give the numbers of blockages and nets, the amount of nets’pins,the range of routing layers,and the die area for each industrial case respectively.

We compare our experimental results generated by our proposed detailed routing process with and without considering the tree-based net’s components points selection firstly. And then, we compare our final optimized results (denoted by Ours)with those generated by replacing A* algorithm in our algorithm with the classic depth-first search algorithm (denoted by DFS). All experiments are performed on the same platform with Intel Core 3.40GHz CPU and 16GB memory for fair comparison.

4.1 Effectiveness of tree-based net’s components points selection

In Section 3.2, two stages of optimization methods are presented to select our connection points of each pin. In order to reflect the effectiveness of the two stages,we test our algorithm with and without considering the tree-based net’s components points selection on the modern industrial benchmarks. The test results are listed in Table 2. In the table, the first column is the names of our industrial benchmarks.The following three columns show the total wirelength(Ltotal(mm)), the total numbers of vias (Vtotal) and routing layers (Rl), respectively. The experimental results show that, our algorithm with the tree-based net’s components points selection can decrease the total wirelength by 82%averagely,and the number of total vias by 10%on the industrial benchmarks.

4.2 Effectiveness of optimizing initial routing result

In this subsection, we compare our final optimized results (denoted by Ours)with those generated by replacing A* algorithm in our algorithm with the classic depth-first search algorithm (denoted by DFS). The test results are put in Table 3.In the table, five evaluation metrics are listed in the second row, that is, out-of-rectangle wirelength (Loc), out-of-rectangle vias (Voc), wrong wires (Lwl), off-track vias(Vot)and actual running time. The experimental results demonstrated in Table 3 show that, our detailed router can complete 100%routability for all different sizes of nets. What’s more, it can satisfy the advanced technology nodes as much as possible, and reduce out-of-rectangle wirelength and vias in a reasonable runtime.

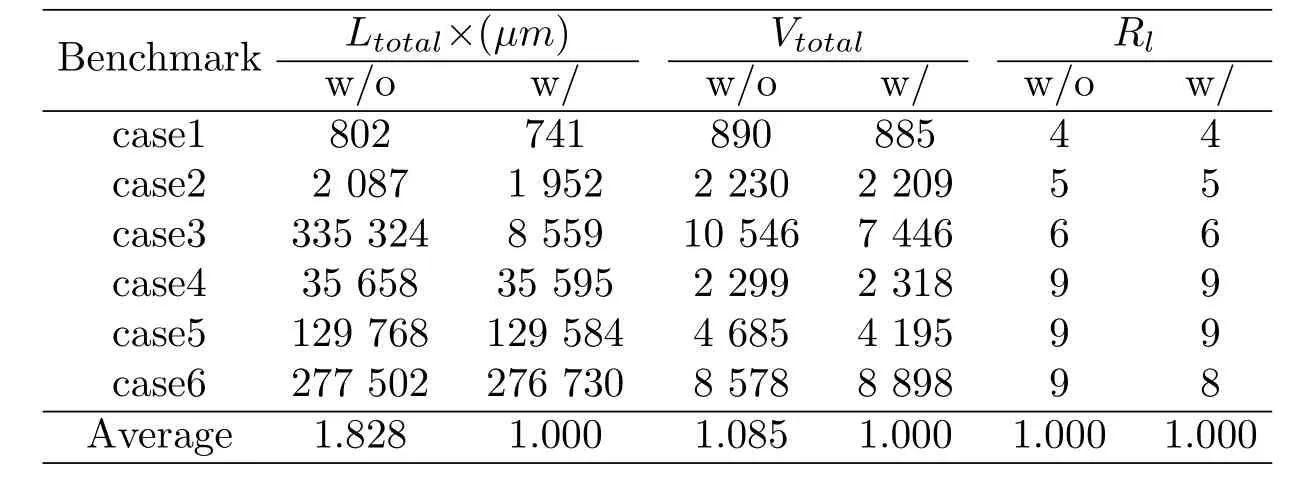
Table 2: Comparison of several metrics without and with our tree-basednet’s components points selection

Table 3: Comparison of final detailed routing results between DFS and Ours

Figure 6 shows our final detailed routing results for Benchmark 3 generated by our algorithm. Figure 6 (a) is the full detailed routing result, and Figure 6 (b) is a partial routing result magnified from Figure 6(a). Furthermore,blue lines in Figure 6 are routed nets and red rectangles are our pin shapes.

5 Conclusion

In this work, an effective algorithm has been presented to solve the modern detailed routing problem. All nets,blockages and pin information are complicated and irregular. The primary purpose of our algorithm is to minimize the total wirelength and total vias by considering the advanced technology nodes. The first two parts of our algorithm focus mainly on preprocessing and local optimizing our pin-access candidates and other connection points of nets. After that,our algorithm completes detailed routing by using an optimized path search method. Experimental results on industrial benchmarks show that, our proposed algorithm not only achieves 100%routability in a reasonable runtime, but also handles connection constraints and honors global routing results efficiently. With the development of modern manufacturing requirements, the detailed routing process with other constraints also need to be further considered in our algorithm.

Figure 6: Full and partial detailed routing results of Benchmark 3