RGBD融合明暗恢复形状的全视角三维重建技术研究

李 健, 杨 苏, 刘富强, 何 斌

（1.陕西科技大学电子信息与人工智能学院，西安，710021；2.同济大学电气与信息工程学院，上海，201804）

引 言

三维重建是指用计算机对三维物体或者三维场景建立可用于表示和处理的数学模型，是在计算机环境下分析其性质以及对其进行操作和处理的基础，也是一种能够把客观世界三维地呈现在计算机上的关键技术。近年来，随着三维重建技术的发展，其研究意义与商业价值越来越凸显出来，并且随着深度相机的广泛应用，用深度相机进行重建成为主流。

（1）RGBD单帧重建

深度相机直接进行重建的精度有限，但如果将其与现有的光照约束重建方法相融合，利用深度相机较之于常规相机所特有的深度信息并结合光照约束,可以在重建精度上有所提高。但是仅通过1张图片，明暗恢复形状(Shape from shading，SFS)方法在光源信息已知的情况下依旧无法确定问题的解[1-2]，并且一般情况下也只能够重建单一反射率的物体。文献[3-4]提出使用区域分割的方法来解决不同反射率的求解问题，但在实际情况中依然很难应对小区域中反射率多变的情况。文献[5]为了解决当前全视角三维扫描系统价格昂贵操作复杂的问题，提出利用1台Kinect和1个回转台来构建全视角三维模型的方法，该方法可以实现三维物体的全视角三维重建，并在精度上优于微软的KinectFusion方法，但是由于Kinect自身分辨率较低，仅使用Kinect深度数据在重建细节上还不能达到标准模型的精细程度。文献[6]采用深度相机融合光度立体的方法进行重建，在重建细节上有了明显的改善，但该方法对重建环境限制较多，如暗室环境、RGB三色光源照射、被建物体单一反射率等。文献[7]提出一种在自然光下对多反射率目标物体的三维重建，可以较好地重建出物体的细节。文献[8]采用深度学习的方法可以方便地从单帧RGB图像当中恢复三维结构。

（2）相邻帧之间的几何配准

不同的相机模型从相机中得到的信息量不同,所以求解的相邻帧间的几何配准也不相同。当使用普通单目相机进行重建时，得到的是图像的二维像素坐标信息，常使用对极几何的方法来估计相机的运动；如果知道一些三维空间点的坐标并且知道其对应在相机中的成像位置，常使用PNP(Pespective-n-point)方法估计相机的运动;当使用双目相机或者深度相机进行三维重建时，或者通过某种方法得到距离信息，也就得出了相邻两帧的点云信息，可以使用点云的特征匹配估计相机的运动。文献[9]提出了利用深度学习shapenet方法进行三维点云几何特征的提取与配准。为了得到较为准确的配准关系，在粗配准的基础上使用迭代最近点（Iterative closest point,ICP）算法进行精配准。

（3）全视角的三维重建

全视角重建过程中逐帧配准存在环闭合问题[10-11]是众所周知的，一个暴力解决的办法[12]是把所有的帧数据通过ICP算法迭代循环，然而这往往需要求解非常大的系统方程。另一个贪婪的解决方案[13]是将每一帧新的扫描数据配准先前的数据上，但它并不能解决配准的误差。文献[14]使用3个深度相机对人体进行全方位的采集并重建，首先通过图像关键点进行相邻帧间的配准，然后进行全局优化。但该方法需要转台进行辅助，并不能用手持相机进行重建。

本文使用Kinect深度相机融合光照约束的方法来实现对三维物体的全视角重建。主要贡献如下：①本文方法不需要借助转台，通过手持Kinect深度相机就能够完成整个三维重建的过程，操作更加方便。②相较于直接由深度相机获取物体的三维信息，本文方法由于融入了物体表面的光照信息，即在原有的深度数据上加上额外的光照约束来优化深度值，因此生成的三维模型更为光顺，也包含了更多物体表面的细节信息，提高了重建精度。③该方法能够在自然光环境下，仅通过单张照片就能够完成对多反射率三维物体的重建，适用范围更广。

1 本文方法总体框架

本文提出的使用Kinect深度相机融合光照约束的三维重建方法流程框架如图1所示。

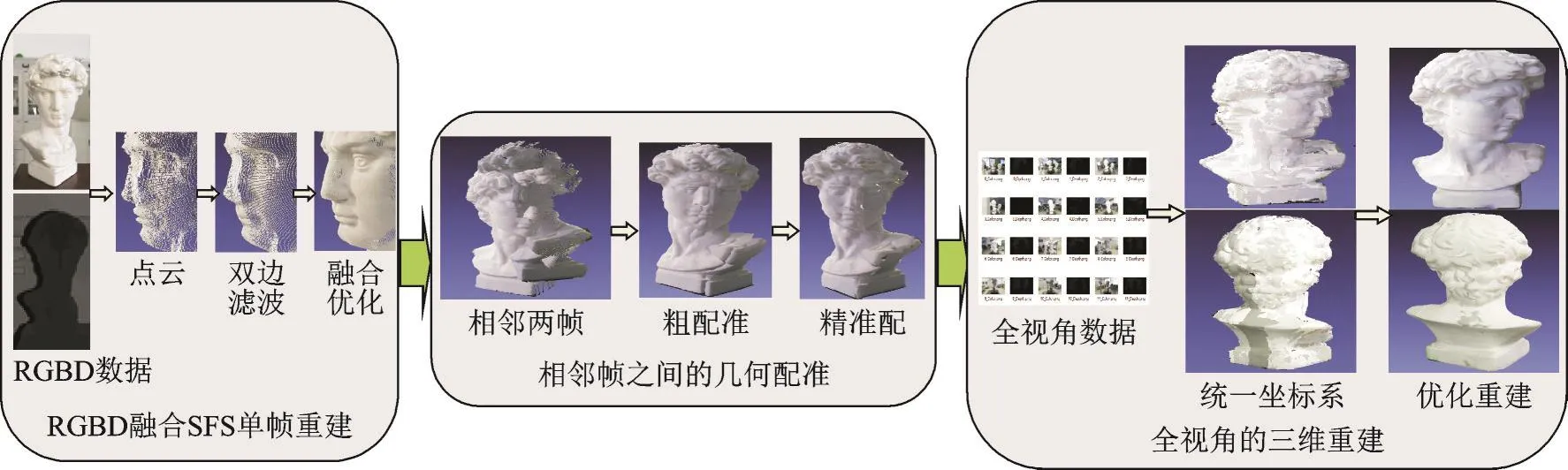
图1 本文方法总体框架Fig.1 Whole framework of the proposed method

2 本文方法详细描述

2.1 RGBD融合SFS单帧重建

2.1.1 深度图像的预处理

首先，在室内自然光环境下使用Kinect深度相机获取被测物体彩色图和深度图,利用相机标定得到的相机内参数和深度图生成点云。根据相机模型可知空间点[x,y,z]和它在图像中的像素信息[u,v,d]有如下关系

式中：cx，cy，fx，fy为相机内参4个参数；d为深度图中的深度信息,单位mm。为了统一单位，需要将深度信息转换为以m为单位,即s变换因子为1 000。

其次,对得到点云数据进行双边滤波去噪，表达式为

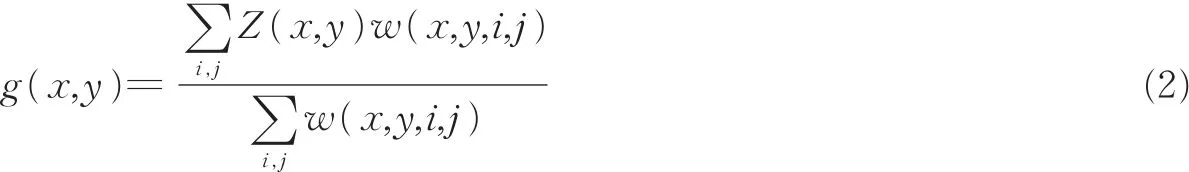
式中：Z(x,y)表示深度图像上点的深度值,求和符号代表的是在当前点的邻域内进行计算；权重系数w包括两部分,分别为值域核wr和定义域核ws，如下所示

式中：σs为空间域标准差；σr为灰度域标准差,i,j为中心像素的坐标；x，y为邻域像素的坐标。从式（3）可以看出,ws随着像素点与中心点之间欧式距离的增加而减小,wr随着两像素灰度值之差的增大而减小。w由以上两项的乘积组成,即w=ws·wr。

2.1.2 SFS问题中光照模型求解

SFS是一种从单幅图像恢复三维信息的方法,本文选择的SFS模型为

式中：L(i,j,n)为光照强度；S(n)为阴影函数；ρ(i,j)为多场景反射率；(i,j)为像素点坐标；n为法线向量。

在求解过程中,本文首先假设朗伯体场景去求解出S(n),然后用优化的方法求解ρ(i,j)。

设置 ρ(i,j)=1,则 S(n)为

m是一阶球谐函数系数,可以通过灰度值I使用最小二乘法优化求解出m,优化公式为

优化出m以后,也就求出S(n),然后对反射率ρ进行求解。由于相近的区域内ρ变化不大,为了防止ρ过拟合,以此为约束,加入先验项,先验项如下所示

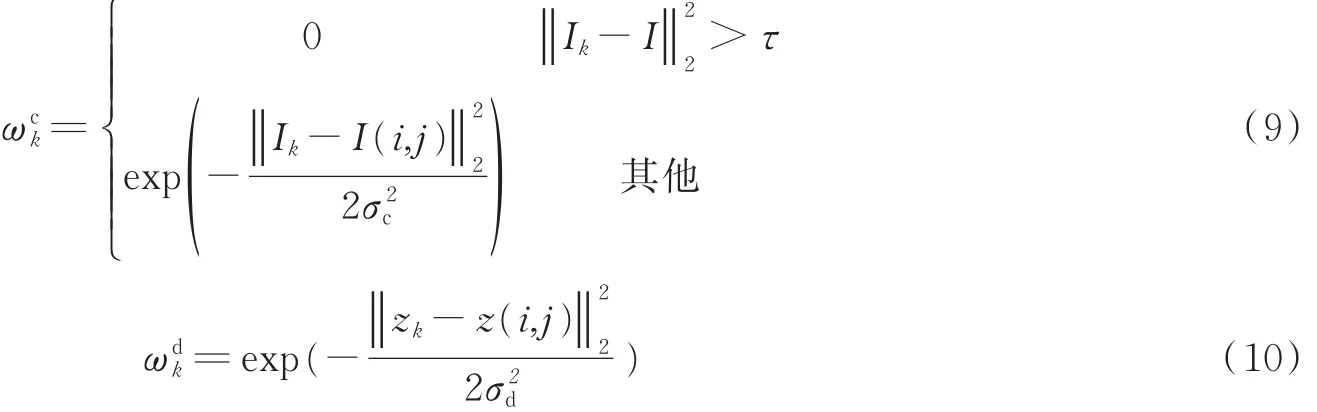
式中：σd为一个允许深度不连续的参数；z(i,j)为深度值。最后用正则化线性最小二乘法求解ρ为

2.1.3 代价函数的构造

现在完整的光照模型已经得到,为恢复物体表面细节,构造出由SFS项、深度项和平滑项3部分构成的代价函数为

式中：Es(∇z)对应 SFS 项；Ed(z)为对应的深度项；El(z)为对应的拉普拉斯平滑项；λs，λd，λl分别对应各自约束项的权重。下面对代价函数中的SFS项、深度项、拉普拉斯平滑项做进一步说明。

（1）SFS项，表达式为

使用SFS的方法改善表面法线,通过正则化项最小化

从式（6）物体表面法线和表面梯度的关系中得出,表面梯度可以由用z的函数表示,然后用最小化灰度值和光照模型的差值即式（13）来求解z值。

（2）深度项，表达式为

式中：z0为初始采集到的深度值；z为估计出的深度值,表示估计出的深度值与原始采集到的深度值的距离。

（3）拉普拉斯平滑项，表达式为

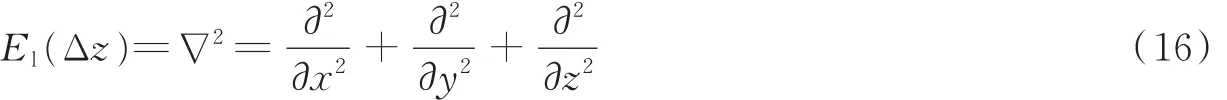
该项的作用是将曲面上非常小的变化、噪声数据很快地扩散到它的邻域中,从而到达平滑的效果。本文为了保证重建结果保留更多的细节，所以设置其权重参数较小。

2.1.4 代价函数的求解

从式（6）物体表面法线和梯度的关系可知，代价函数的SFS项是非线性部分，本文求解思路是首先求解出线性部分，然后进行非线性部分的求解。采用迭代的方式，从1个初始值出发，不断更新当前优化变量，使代价函数下降，直到某个时刻代价函数值最小，此时算法收敛。

对法向量作如下变形

对应的新的线性光照模型为

对应的代价函数为

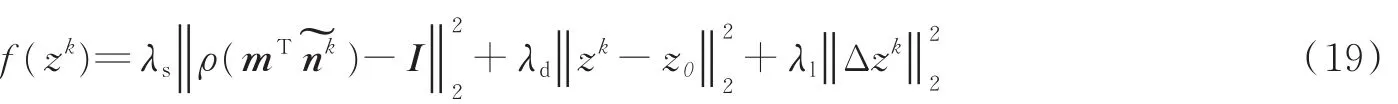
算法的输入包括z0，m，ρ(i,j)等光照模型参数，输出为zk，求解的步骤为当f(zk-1)-f(zk)＞ 0，循环执行：（1）令=(nk,1)T；（2）更新 L(i,j,∇z)= ρ ·(mT)；（3）最小化式（19）求解出 zk。

2.2 相邻帧之间的几何配准

求解相邻帧之间的几何配准主要有两部分组成：快速点特征直方图（Fast point feature histograms,FPFH）特征匹配求解粗配准矩阵和ICP算法求解精配准矩阵，两矩阵间的乘积即为相机间的几何配准关系。

2.2.1 FPFH描述子搜索对应点

FPFH是一种空间局部点特征描述子，通过计算查询点与其K邻域内元素的法线之间的关系来表示点云表面的变化情况，并通过一个多维直方图对点云的几何特性进行描述。FPFH计算的影响区域如图2所示。

查询点Pq位于图2中半径为r的球形中心，查询点与其所有K邻元素相互连接。为方便计算两点间的关系，在UVW坐标系中计算任意两点Pt和Ps及与它们对应的法线ns和nt之间的相对偏差。UVW坐标系如图3所示。

图3中U，V，W分别表示3个方向，即

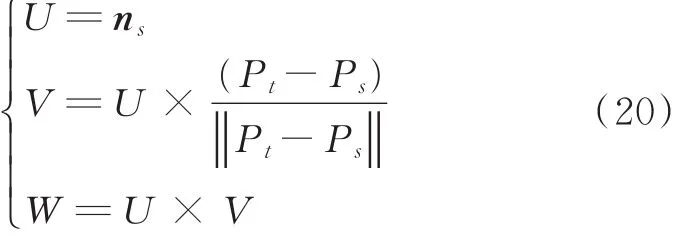
使用UVW的坐标系，法线ns和nt之间的差可以化解为下面3个角度的差异

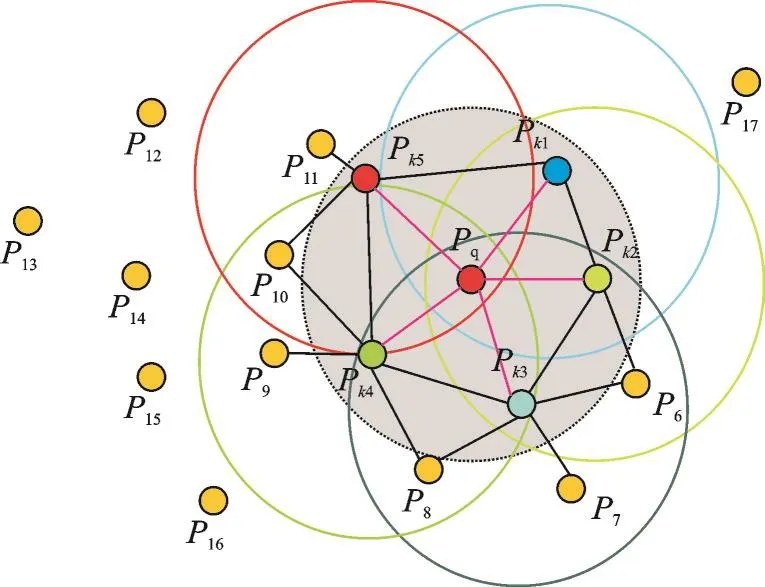
图2 FPFH影响区域示意图Fig.2 Schematic diagram of FPFH affected area

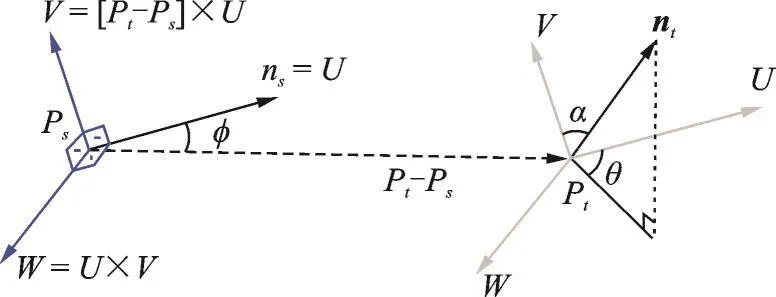
图3 UVW坐标示意图Fig.3 Schematic diagram of UVW coordinate

分别将α，β，θ从0°～360°等分为11个区间，创建一个有33个等分区间的直方图，每个区间对应特定范围内特征值的个数。按照如下步骤计算查询点的FPFH值：

步骤1 计算查询点Pq与其影响区域内所有点的3个特征值，统计每个区间所对应的特征值的个数，得到简化的点特征直方图SPFH。

步骤2 重新确定每个点的K邻域，根据式(22)使用邻近的SPFH计算最终的FPFH。

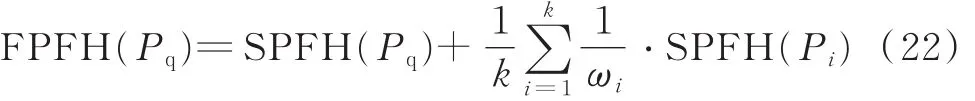
式中：Pk为Pq的邻域点；权重ωk为Pq与Pk之间的距离；K为邻域点Pk的个数。

计算得到的FPFH如图4所示，图4(b)为4(a)中红点的FPFH。

2.2.2 RANSAC滤除误匹配

图4 快速点特征直方图示例Fig.4 Example of FPFH

通过比较FPFH值得到的对应关系并不完全正确，采用随机采样一致性（Random sample consensus,RANSAC）算法剔除其中的错误匹配，能够得到相对准确的对应关系。

RANSAC算法是一种简单有效的去除误匹配的方法，通过建立一个特定的数学模型将数据点分为“内点”和“外点”，采用迭代估计的方法计算出最优参数模型，找到的不符合该模型的“外点”为误匹配点，符合模型的“内点”为精确匹配。以图5为例，图中实线对应正确匹配，线条两点为“内点”，虚线为误匹配，线条端点为“外点”。

RANSAC步骤结束后可以得到较为正确的匹配关系。但由于FPFH计算方式描述的是查询点与其邻域点之间的关系，这一特性导致在点云表面曲率变化较小或者点云密集的区域中相邻点的FPFH值非常接近，因此可能会发生对应到正确匹配附近点的情况，如图5中2号对应关系所示，由于相邻点的FPFH值非常接近，所以根据特征值判定图5中2号线两端的点为对应点。该对应关系虽不完全准确，但却在RANSAC步骤所建立数学模型的容差范围内，所以认定其为正确匹配。这种不准确的映射关系会对配准结果产生负面影响，这也是需要精配准步骤的原因。

2.2.3 ICP算法精配准

ICP算法的主要思想为：假设有2个待配准的三维点集A和B，对A进行平移和旋转变换，使得2个点集对应点之间的距离尽量小，然后取一个代价函数来表示该距离，最后用优化的方式求解出两组点云间的配准变换矩阵R和T。

假设点云数据集为A{Pi，i=1,2,3,…,M}，点云数据集为B{Qi，i=1,2,3,…,M}，其代价函数为

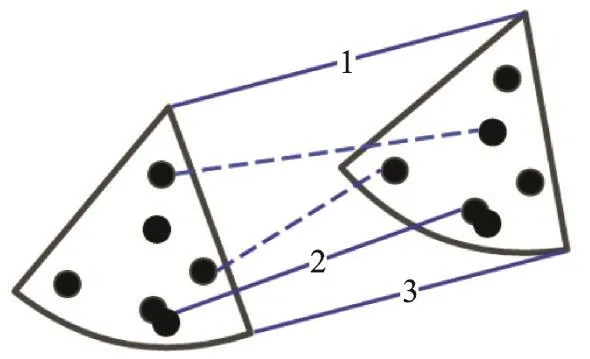
图5 RANSAC示意图Fig.5 Schematic diagram of RANSAC

式中：k为点云数据集A和B之间匹配点的总数量，求和符号计算的是所有匹配点间欧氏距离的平方和。

2.3 全视角的三维重建

得到了相机间变换关系后，要想把所有帧进行拼接，必须选择一个原点坐标系，并把其他帧进行坐标变换，统一在此坐标系中。由于累积误差的存在，第1帧和最后1帧不能完全重合在一起，所以需要进行全局优化，本文借鉴了光束平差法（Bundle adjustment,BA）算法，其整体的代价函数为

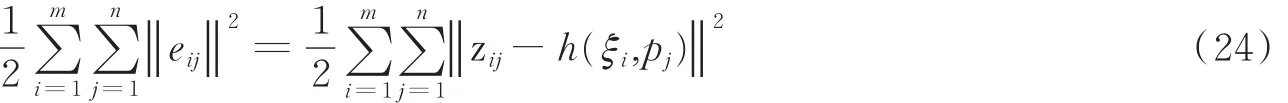
式中：误差项e为得到的空间点投影在平面中的像点与真实的平面中的像点之间的误差。世界坐标系中的一个点p，通过相机内外参数最后投影成像素坐标的整个过程可用观测方程h(ξ,p)表示，其中李代数ξ代表相机外参R及t，p为三维点坐标。

优化后使用泊松重建的方法来对点云进行表面重建，重建的结果是一个封闭的曲面，该结果不仅可以得到精度较高的细节信息，而且还能够减小噪声产生的影响。

3 实验结果分析

实验系统由1台PC机和1台Kinect For Windows 2.0传感器组成，三维重建物体为大卫石膏像，实验时手持Kinect深度相机绕大卫一周连续采集其信息，即深度图和彩色图，然后离线处理。考虑到如果把所有采集的图像信息进行重建，数据量过大且重建重叠区域较多，重建效果不好，所以从中选出12帧，这样既能保证数据量也可以较好地得出两帧间的变换矩阵。重建数据如图6所示。

3.1 单帧重建

通过实验比较，选择合适参数如下：空间域标准差 σs=8，灰度域标准差 σr=15，ρ的先验项权重 λρ=0.1，SFS 项 权重 λs=1，深 度项权 重λd=0.4，拉普拉斯平滑项权重λl=0.007 5。对石膏像单帧重建结果如图7所示，为了更好地展示重建结果，对其面部细节进行放大。

为了比较本文方法与其他方法的重建精度，首先使用Artec扫描仪扫描得到目标物体标准的三维模型，然后再将不同方法重建出的结果与标准模型进行注册配准，最后计算两者之间对应点的最近几何距离，并用伪彩色表示，如图8所示。图8(a)是文献[7]重建后的点云数据与三维模版进行比较的伪彩色图，图8(b)是文献[5]重建后的点云结果与三维模版进行比较的伪彩色图，图8(c)是本文中方法重建结果与三维模版进行比较的伪彩色图。三者平均误差和均方根误差如表1所示，从结果中可以看出本文中的误差更小。

图6 实验数据Fig.6 Experimental data

图7 石膏像单帧重建结果Fig.7 Single frame reconstruction results of the plaster model

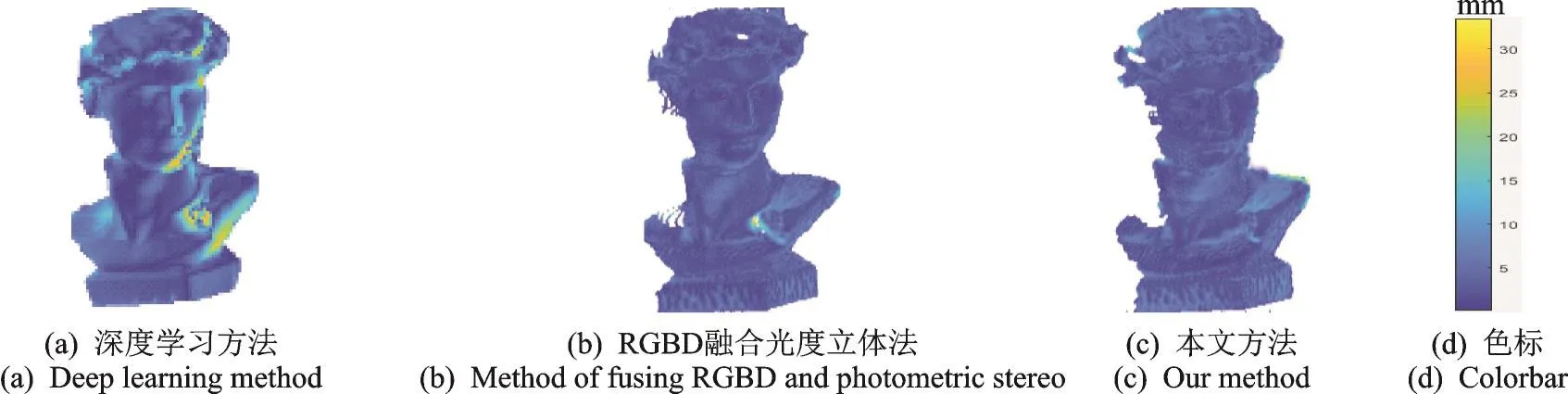
图8 伪彩色图Fig.8 Pseudo-color graph

表1 误差比较Table 1 Error comparison mm

3.2 相邻帧之间的配准

相邻帧之间的配准结果如图9所示，图9(a)表示未融合SFS重建后点云数据粗配准结果，图9(b)表示本文方法重建后点云粗配准结果，图9(c)表示本文方法重建后ICP精配准后的结果，图9(d—f)表示对应图9(a—c)配准误差的伪彩色。

从图9(a，b)的红色标注部分可以看出，本文融合SFS重建后进行粗配准效果更好，验证在点云数据质量更高的基础上使用本文方法可以有效地改善粗配准的结果。此外，从图9(b，c)，(e，f)的比较也表明了精配准的有效性。其配准误差如表2所示。求解出相邻帧间的变换关系是包含旋转平移的4×4的矩阵，如表3所示。

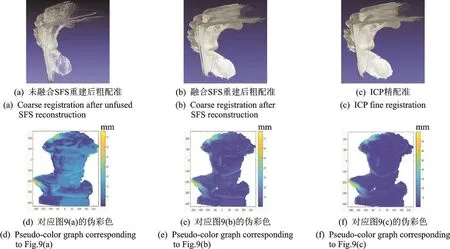
图9 相邻帧的配准结果Fig.9 Registration results of adjacent frames

表2 配准误差Table 2 Registration error mm

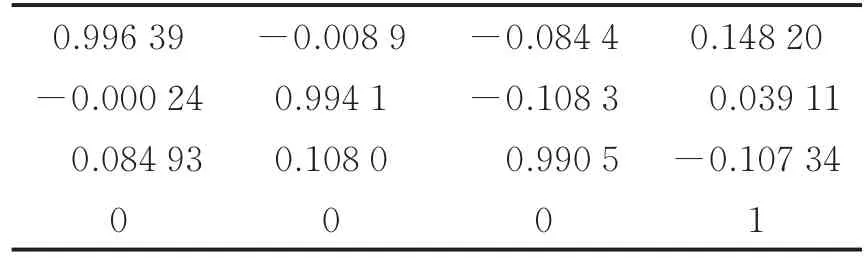
表3 变换矩阵Table 3 Transformation matrix

3.3 全视角的三维重建

得到相邻两两帧之间的变换关系后，为了方便重建，选择最后1帧作为坐标原点，然后统一坐标系。实验处理数据共12帧，编号从0—11定义矩阵变量，例如t10_11表示第10帧到第11帧之间的变换矩阵，如表3所示。t9_10表示第9帧到第10帧之间的变换矩阵，则第9帧到第11帧的变换关系为t9_10和t10_11两矩阵的乘积。以最后1帧作为原点坐标系，统一坐标系逐帧拼接结果如图10所示。

由于累积误差的存在，在首尾帧处会出现闭合不了的现象，在本文中即在大卫石膏像背部，由于视角的问题，从侧面和底部进行展示所有点云数据统一坐标系后的结果。如图11所示，其中图11(a，b)红色标注为由于累积误差造成的影响。可以看出，首尾帧没有平行重合，出现了分层的现象，图11(b)也显示出原本是直线的模型底座出现断裂弯曲。

为了消除累积误差，采用光束平差法来进行优化，重新调整相机的位姿，其优化后的结果如图12所示。比较图11，经过全局优化算法后有效地消除了累积误差，使首尾帧完全重合。

全局优化后的点云数据首尾帧可以完好地重合在一起，接下来要使用点云融合去除重复点，并使用泊松重建表面，其结果如图13所示。从重建结果可以看出，经过点云融合和泊松重建后的模型表面更加光滑。

图10 逐帧拼接Fig.10 Splicing frame by frame

图11 累积误差Fig.11 Accumulative error

图12 优化后的结果Fig.12 Optimized results

图13 重建结果Fig.13 Reconstruction results

为了比较本文方法重建精度，把Artec扫描仪得到的三维模型作为标准模型，将不同方法重建出的三维模型分别与标准模型进行配准，然后计算出与标准模型上最近点的距离，最后用伪彩色图来表示该距离，如图14所示，其误差比较如表4所示。

图14 伪彩色图Fig.14 Pseudo-color graph

表4 算法误差比较Table 4 Error comparison of different algorithms mm

4 结束语

本文使用深度相机融合SFS光照约束完成对物体的全视角三维重建。本文方法不需要借助转台，手持深度相机就可以方便地完成对三维物体的全视角重建；相较于直接由深度相机获取物体的三维信息，本文方法由于融入了物体表面的光照信息，即在原有的深度数据中加上额外的光照约束来优化深度值，因此生成的三维模型更为光顺，也包含了更多物体表面的细节信息，提高了重建精度；相较于光度立体法，该方法在自然光环境下，仅通过单张照片就能完成对多反射率三维物体的重建，适用范围更广。但是，由于该方法受深度相机的制约只能用于室内重建，对光照约束也只考虑了朗伯体漫反射的情况，所以下一步在重建更复杂的三维场景时，还需要进一步考虑环境光和镜面反射光等其他光照模型对整个工作的影响。