超声振动辅助ELID复合内圆磨削系统中大负载变幅器的设计及应用*
2020-03-13贾晓凤
贾晓凤, 赵 波
(1.安阳工学院 机械工程学院, 河南 安阳 455000)(2.河南理工大学 机械与动力工程学院, 河南 焦作 454150)
随着科技进步与生产技术的发展,硬脆材料(如碳化物、半导体材料、陶瓷、光学玻璃等)已在工业生产中广泛应用[1-4]。硬脆材料的镜面高效加工技术作为超精密加工技术的重要分支,对航空航天、微电子与光电子等高精尖技术的发展具有重要意义[5]。
在线电解修整砂轮磨削技术(即ELID磨削技术)由OHMORI等[6]提出,可以边磨削边修整砂轮,从而维持金刚石砂轮恒定的出刃高度和容屑空间,改善了传统磨削过程中砂轮易堵塞的问题,可获得纳米级加工表面。超声振动辅助加工技术[7]是在原有机械加工基础上将高频振动附加在工件或者工具上,产生空化、冲击、泵吸效果,抑制校正作用及砂轮表面氧化膜的筛选作用等,对降低磨削温度、提高加工效率及降低工件表面粗糙度具有显著作用[8-10]。将这2种加工方式优势互补,形成一种适用于加工硬脆材料内环面的加工技术——超声振动辅助ELID复合内圆(ultrasonic vibration assisted ELID internal,UAEI)磨削技术[11],其装置如图1所示。图1中产生高频振动的超声振动系统是UAEI磨削装置的重要组成部分,由换能器、变幅器和工具头(金属结合剂金刚石砂轮)组成,变幅器将换能器端面的小振幅扩大,并将超声能量聚集至工具头,减小了谐振阻抗,使工具头在谐振频率工作,提高了声电转化效率。
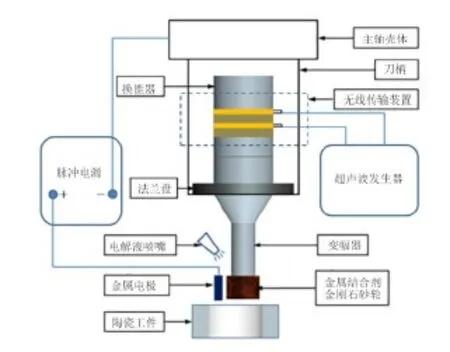
图1 UAEI磨削装置示意图
为获得良好的内圆磨削效果,砂轮直径与工件内圆直径比值通常在0.5~0.9之间,砂轮高度应接近于工件高度[12]。由于UAEI系统中的驱动砂轮需采用金属结合剂金刚石砂轮才能参与在线电解修整,故针对内圆直径较大的工件,需匹配体积大、直径大、质量重的大负载工具头砂轮。所以,设计出能驱动此种砂轮的变幅器是研制UAEI磨削系统的关键。
目前,对带有工具头的变幅器设计通常首先采用传统解析法[13-14]、等效电路法[15]、四端网络法[16]等,再结合有限元仿真设计,但这些设计方法存在理论设计过程烦琐、计算量大、计算精度不理想等问题。由于工具头的几何尺寸、质量大小以及与变幅器的连接方式都对超声共振系统有很大影响[17],因此此类工具头的设计有较大局限性。
本研究基于弹性波在介质中的传导定律,将几何尺寸大且质量大的金属结合剂砂轮与变幅器作为一个整体进行有限元优化设计和振动测试,使整个振动系统达到谐振状态,并对最终研制出的UAEI系统进行加工特性测试。
1 大负载变幅器设计及仿真优化
1.1 变幅器理论分析
基于弹性波在介质中的传播规律可知,当声波从一种介质传递到另一种介质时,在交界面会存在一定的入射角,发生波形转化,导致波能量转移。弹性波在介质中传播时,一般有纵波和横波2种形式,变幅器在超声作用下的振动行为实质是弹性波在有限介质中的传播问题。在设计纵振变幅器时,将变幅器等效为均匀棒,当变幅器直径(横向尺寸)小于该频率下纵波的1/4倍波长时,可忽略横波在介质中传播的影响[18]。当纵波以一定角度自介质1入射到介质2中时,发生折射和反射,设v1和v2分别是2种介质中的波速,θ1和θ2分别为其入射角、折射角。根据折射定律知[19],当纵波自波密介质传播至波疏介质时,若入射角θ1为临界角θ0时,则折射波会沿折射界面的切线方向传播,折射角为90°,此时,有sinθ2=1;若入射角θ1>θ0时,sinθ2>1,此种情况不存在,没有物理意义,此时只有反射波,没有折射波,波发生全反射。临界角θ0表达式为:
θ0=arcsin(v1/v2)
(1)
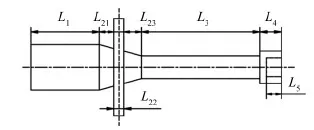
以纵向振动频率f=25.0 kHz为目标设计频率,为了减小变幅器过渡结构的应力,拟采用圆锥过渡的阶梯式复合变幅器设计形式,其外形及波传播路径如图2所示。图2中,L0是换能器前盖板长,L1是变幅器大端长,L2是变幅器圆锥段长,L3是变幅器小端长,L4是金刚石砂轮高度,DL为变幅器大端直径(同时也是换能器晶片直径),DS为变幅器小端直径,Dg为砂轮直径,S1为变幅器大端截面面积,S2为变幅器小端截面面积,λ1为入射波波长,λ2为反射波波长,αx为入射波与圆锥段母线的夹角,βx为反射波与变幅器轴线的夹角。
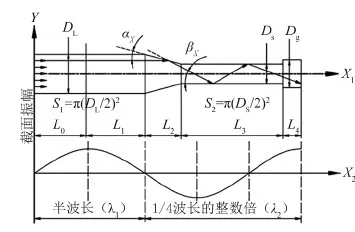
图2 波在变幅器中的传播路径示意图
需要加工的环形陶瓷工件为ZTA纳米复相陶瓷材料。砂轮采用粒度为M36/54、浓度为100%的铸铁结合剂金刚石砂轮,变幅器材料为45#钢,三者具体参数如表1所示,45#钢的物理参数如表2所示。表1中砂轮的形状尺寸是根据工件形状尺寸选定的[12]。购买25.0 kHz的夹心式换能器;变幅器小端长L3的取值范围根据内圆磨削加工空间和刚度要求制定,变幅器大端直径DL由换能器晶片直径36 mm确定,变幅器小端直径DS根据砂轮与变幅器的连接方式(螺纹连接)和已确定的变幅器大端直径DL确定。
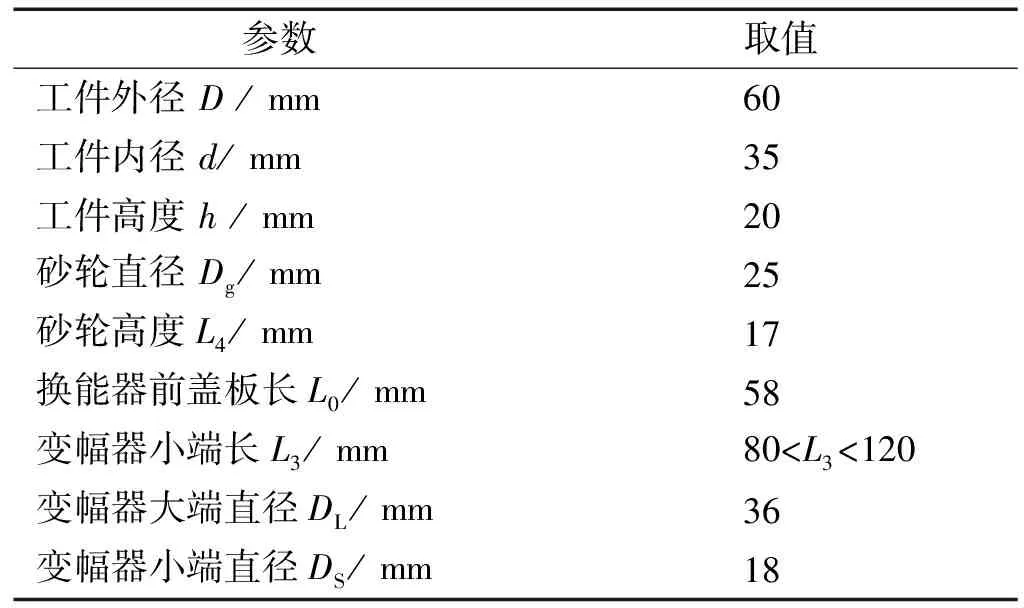
表1 环形陶瓷工件、砂轮及变幅器形状参数

表2 45#钢的物理参数
由图2可知:换能器产生的简谐机械波自变幅器大端传递到圆锥过渡面,由于纵波在45#钢中的传播速度(5 169 m/s)远大于其在空气中的传播速度(344 m/s),其入射角不会小于临界角,故在圆锥面只发生反射,不会发生折射。发生的反射波与单一纵波比例可以由变幅器大端截面的面积S1和小端截面的面积S2的比值确定。根据表1中的DL与DS值,可以估算出发生角度反射的波占总波数的比例为(1-S2/S1)×100%=75%。因此,变幅器设计时应该优先保证这75%的纵波沿一定角度反射后到达砂轮末端的振幅最大。
纵波传至变幅器的圆锥段时,一部分纵波会产生径向传播。由于存在径向振动,使系统总动能产生变化,系统惯性增大,均匀棒(变幅器等效而成)的等效分布参数发生变化,从而影响波的传播速度[20]。取其中一束波作为研究对象,其与圆锥段母线夹角为αx,反射后与变幅器轴线夹角为βx(图2所示),据几何关系知:
(2)
由于变幅器在圆锥段L2内有75%纵波发生反射,为了便于计算,假设入射波速c1在整个圆锥段L2都转化成了反射波速c2,将圆锥段L2、变幅器小端L3和砂轮高度L4作为一个整体,按反射波速c2的1/4倍波长的整数倍设计,则有关系式:
(3)
由公式(2)和公式(3)可得:
(4)
由于简谐波振动的零点位置是换能器的压电陶瓷片与换能器前盖板L0的接合处,且前面分析已知:在圆锥段L2处仅有75%的纵波发生角度反射,25%的未反射。为了便于计算,将换能器前盖板L0与变幅器大端L1作为一个整体,按原波速的半波长设计。已知换能器前盖板尺寸L0,可推导出L1=λ1/2-L0=45 mm,其中入射波波速c1对应的波长取整值λ1=c1/f=206 mm。因此,带工具头的整个变幅器未确定几何尺寸参数的只有圆锥段长L2和小端长L3,但二者有式(4)的关系,且表1中已给出L3范围。
1.2 变幅器设计
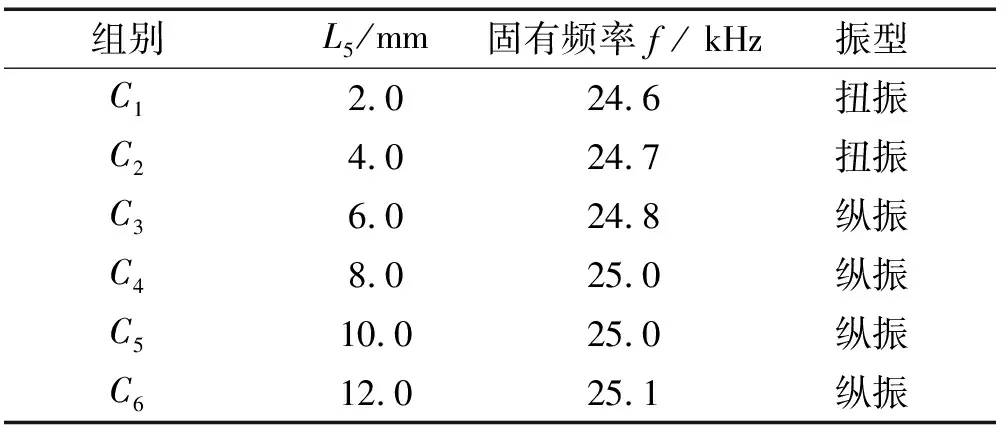
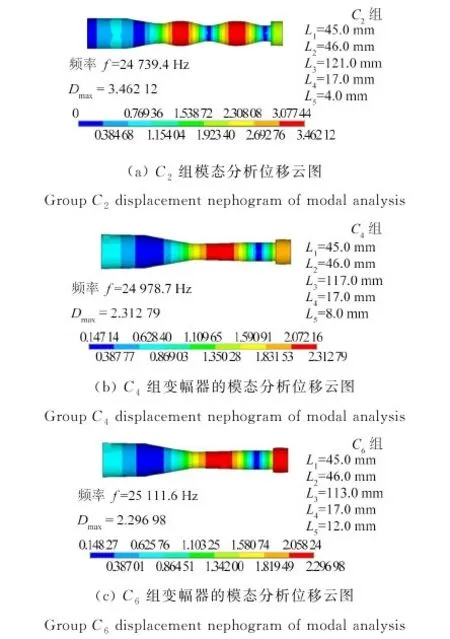
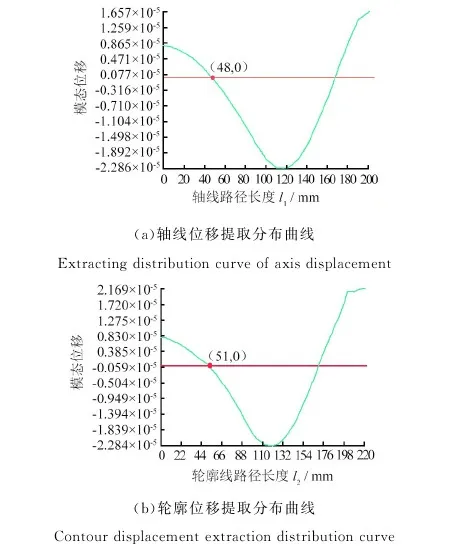
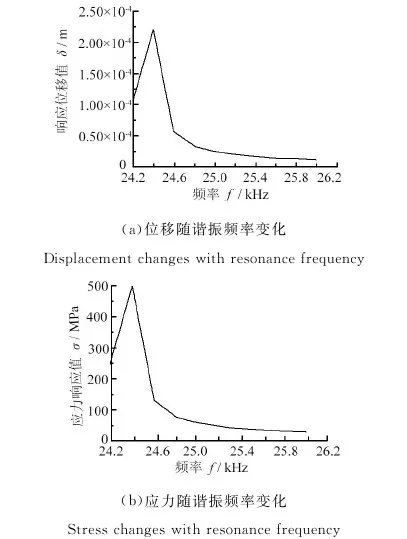
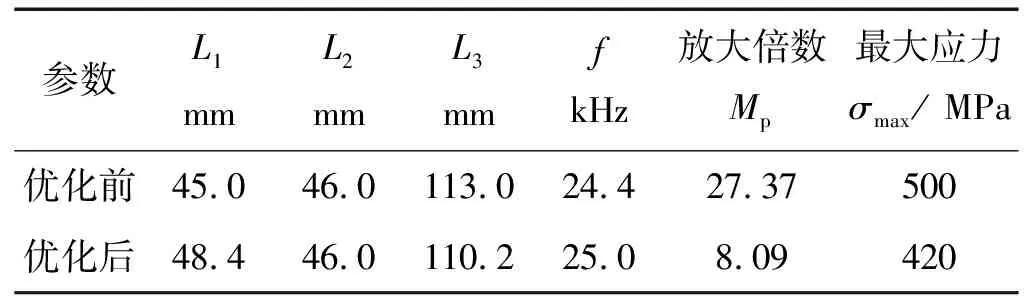
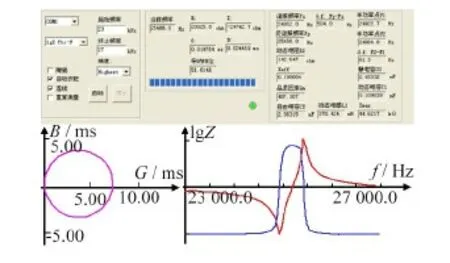
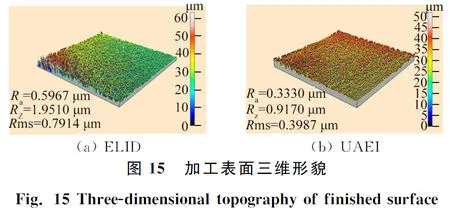
由表1可知,变幅器小端长L3需满足80 mm 图3 不同L3值下的L2的理论值 表3 变幅器理论取值方案 图4为A2、A4、A6和A84组变幅器模态分析对比图,图中的不同颜色代表不同的相对位移量(从红色到蓝色相对位移量依次减小),反映了变幅器在各阶固有频率下的振动特性。由表3和图4发现:A2、A4、A83组参数下的变幅器产生纵向振动,其固有频率分别为26.9 kHz、26.7 kHz、20.8 kHz;而A6组产生扭振,不符合纵向振动模式要求。UAEI磨削要求在线电解装置中的金属电极在整个加工过程中与砂轮保持相对静止,为了便于安装固定金属电极,要求变幅器小端长度L3在允许范围内尽量长,圆柱段L2在允许范围内尽量短。因此,初步选取合适的A4组,以进行后续分析及优化。 (d)A8组模态分析位移云图 A4组的固有频率是26.7 kHz,与目标设计频率25.0 kHz存在一定偏差,且砂轮处未呈现红色,说明砂轮的纵向位移(1.598 39)小于其综合最大位移Dmax(仿真云图上的值2.306 22),即砂轮振幅未达到整个变幅器振幅的最大值,拟通过改变变幅器小端L3长度和对砂轮进行开孔处理的方式进行修正。在其他条件不变的情况下,在允许范围内只改变小端长度L3值进行B组试验,并进行ANSYS模态分析,试验方案及试验结果如表4所示。 表4 改变变幅器小端长度L3试验方案及结果 从表4中的试验结果可知:随着小端长度L3增大,变幅器固有频率逐渐下降。本着L3在一定范围内越长越好的原则,选择B6组。图5为B6组变幅器的模态分析图,观察图5发现:砂轮振幅未达到整个变幅器振幅的最大值。因此,在B6组基础上对砂轮开孔L5并进行C组试验,并进行模态分析。砂轮开孔后的变幅器结构如图6所示,试验方案及结果如表5所示。 图5 B6组模态分析位移云图 表5 改变砂轮开孔深度L5试验方案及结果 图6 砂轮开孔的变幅器结构示意图 表5条件下的C2、C4及C6组变幅器模态对比图列在图7中。综合表5和图7可发现:在B6组基础上,在保证其他尺寸不变的情况下对砂轮进行开孔处理后,随着开孔深度L5加深,变幅器固有频率逐渐增大并趋近于目标设计频率25.0 kHz。至C6组时,固有频率达25.1 kHz,且此条件下砂轮处的纵向位移等于综合最大位移Dmax,即砂轮振幅达到整个变幅器振幅的最大值。 图7 不同组变幅器模态分析对比 Fig.7 Model shapes of amplitude device in different group 需要注意的是,在超声加工过程中,变幅器通过法兰盘固定安装在刀柄上,与其他系统共同工作。为了尽可能减小系统阻尼,通常情况下选择系统轴向位移为零处(即位移节点处)来设置法兰盘[23]。若法兰盘位置选择不当,将会造成工作过程中法兰盘振动强烈,导致系统发热严重,使能量大大损耗,因此合理确定法兰盘位置十分关键。 为更加直观观察变幅器位移分布情况并确定法兰盘位置,利用ANSYS路径读取功能提取其轴线位移及轮廓位移,其对比图如图8所示。图8中的2种节点提取方式均各有2个节点,但由于法兰盘的功能性决定了设计时需寻找靠近变幅器大端的节点位置,故图8a的轴线位移靠近变幅器大端的节点位置在(48.0 mm, 0)处,而图8b的轮廓线位移靠近变幅器大端的节点位置在(51.0 mm, 0)处,2种提取方式的节点位置略有偏差,说明同一时刻变幅器同截面的圆心上的质点相对圆周上的质点具有相对位移。由于实际安装法兰盘时采用紧固螺钉与刀柄连接的方式,法兰的位移约束由轴线到圆周面越来越强,故选择轮廓位移节点作为法兰盘的中心位置更符合实际加工情况。 图8 轴线及轮廓位移提取对比 放大倍数Mp是反映变幅器振幅放大性能的重要参数,指共振频率下变幅器的输出端和输入端的质点位移之比[18]。由于图6的砂轮端面做了开孔处理,由图8b的轮廓位移提取结果知:放大倍数Mp应取砂轮小端端面圆周质点模态位移2.169×10-5与变幅器大端端面圆周质点模态位移0.830×10-5的比值,即放大倍数Mp为2.61。 图9为最后加法兰盘、砂轮开孔处理的变幅器结构示意图。在变幅器轮廓位移节点位置(51.0 mm, 0)处加上法兰盘,具有连接固定作用的法兰盘厚度设定为L22=8.0 mm,则L21=2.0 mm,L23=36.0 mm,对加上法兰盘后的变幅器进行模态分析,得到其固有频率为25.2 kHz。同时,采用Full法[24]进行谐响应分析,扫频范围设定为24.0~26.0 kHz,子步数为10。求解完成后,进入ANSYS后处理模块,观察节点位移响应值、应力响应值与谐振频率之间的关系,如图10所示,此时变幅器的共振频率为24.4 kHz,小于目标设计频率25.0 kHz。当激励频率与共振频率同频时,产生峰值响应,纵向位移达到最大值,同时应力达到最大值。此时的应力最大值为500 MPa,超出了45#钢的许用应力强度480 MPa,不符合实际生产需求。 图9 加法兰盘、砂轮开孔处理的变幅器结构示意图 图10 谐响应分析结果 为了使加上法兰盘后的变幅器的谐振频率与实际工作频率更接近,且使其最大应力在材料的允许应力强度范围内,将大端长L1和小端长L3作为变量进行微调优化。具体优化过程如下: (1)定义优化设计变量:43 mm≤L1≤47 mm,110 mm≤L3≤116 mm; (2)定义优化状态变量:谐振频率-1000 Hz≤搜索频率≤谐振频率+1000 Hz,0 MPa≤最大应力值≤480 MPa; (3)设置目标函数:放大系数的倒数为1/Mp; (4)指定优化设计方法:采用零阶算法[24],迭代次数30次。 完成以上优化步骤后即可求得如表6所示的优化结果。 表6 零阶算法优化结果 表6的优化结果显示:虽然放大倍数减小了,但最大应力在45#钢的许用应力范围内,且满足设计频率25.0 kHz的要求。优化的实质是在满足材料许用应力的情况下,最大限度地增大放大系数。优化后的位移分布云图如图11所示,图11中的砂轮振幅达到整个变幅器振幅的最大值,且振型良好。 图11 变幅器优化后的位移分布云图 采用阻抗分析仪(型号Impedance Analyzer PV70A)对优化后的变幅器进行阻抗测试,测试结果如图12所示。 图12 阻抗分析结果 图12中优化后的变幅器谐振频率为24 952 Hz,反谐振频率为25 456 Hz,相对于目标设计频率25.0 kHz的误差为0.192%~1.824%;且导纳圆是个封闭圆,未出现寄生圆,电导曲线正常;振动系统的机械品质因数Qm=407.107,品质因数较高,说明变幅器工作时振动频率较稳定,重复性好。因此,优化后的变幅器尺寸及振动性能均能满足设计需求。值得注意的是,变幅器实测频率和仿真优化所得到的频率有一定差别。原因是:变幅器所用材料实际物理性能参数和理论设计参数有一定差别;另外,实际加工出的变幅器也存在形位误差和尺寸误差。 为了测试变幅器的振幅能否达到实际生产加工要求(振幅要求达到8 μm),更加直观地说明变幅器优化设计的效果,对优化后的超声振动装置的振幅进行测量。选用25.0 kHz大范围自动跟踪超声波电源对振动系统进行供电,电源的跟踪频率范围为2.0 kHz,采用型号HK-008W的激光位移传感器对变幅器输出端振幅进行测量,测量结果如图13所示。从图13中可以看出该超声振动装置的振幅达到了8.0 μm,振形稳定且呈周期性变化。 图13 振幅测试结果 将设计好的变幅器安装在刀柄上,加工特性测试试验在UAEI磨削试验平台上进行,如图14所示,试验平台主要由电火花整形装置、工件旋转装置、在线电解装置和超声振动声学装置等组成。 图14 UAEI磨削试验平台 分别采用ELID内圆磨削和图14的UAEI磨削试验平台磨削方式加工环形陶瓷工件的内环面。通过控制超声波发生器开关改变磨削方式,关闭超声波发生器时为ELID内圆磨削,超声振幅为0 μm;打开超声波发生器时为UAEI磨削,超声振幅为8.0 μm。加工特性对比试验参数如表7所示。 表7 加工特性对比试验参数 工件表面三维形貌采用白光干涉仪(型号Talysurf CCI6000)测量,砂轮表面微观形貌由超景深三维显微系统(型号KEYENCE VHX-2000)观察,测量结果如图15、图16所示。 观察图15可知:ELID内圆磨削形成的加工表面粗糙度为0.596 7 μm(图15a);保持其加工条件不变,开启超声波电源,切换至UAEI磨削模式,形成的加工表面粗糙度为0.333 0 μm(图15b),相比较ELID内圆磨削,工件的表面粗糙度值降低了44.2%,且工件的三维形貌更加平整。形成的原因是超声振动提高了游离磨料划擦工件表面的频率,加工效果相当于微细磨粒的超声研磨抛光,从而有效提高了内环面的表面质量。 观察图16可知:ELID内圆磨削后的砂轮表面氧化膜有微小裂纹和坑洞(图16a),而UAEI磨削后的砂轮表面磨粒凸出数量增多,表面氧化膜裂纹减少,质地更密实(图16b)。原因是UAEI磨削中砂轮作轴向高频振动,一方面强化了砂轮的自锐性;另一方面,相较于ELID内圆磨削,UAEI磨削增大了阴、阳两电极之间的相对面积,增强了电场中电力线的重合率,增大了氧化膜的生成量,在工件的碾压作用下,氧化膜的质地更为密实,有利于辅助保持磨粒的切削作用[25]。 (1)提出了一种应用于UAEI磨削系统的大负载变幅器的设计优化模式,即:基于弹性波传播规律,利用MATLAB确定变幅器几何取值方案,结合模态分析筛选出进一步优化的方案;然后将轮廓零点位移值作为节点位置;最后采用零阶算法对加法兰盘的变幅器进一步优化处理,设计出了满足几何尺寸、应力及振动频率要求的变幅器,使砂轮的动力学特性满足加工需求。 (2)对设计出的变幅器进行振动特性测试,与目标设计频率25.0 kHz相比,其误差为0.192%~1.824%,且变幅器工作时振动频率稳定,稳定工作时振幅达到8 μm,符合预期设计要求。 (3)进行ELID内圆磨削和UAEI磨削陶瓷内环面工件对比试验,发现超声振动的引入可增强砂轮自锐性,有利于砂轮表面质地密实氧化膜的形成;且UAEI磨削形成的加工表面粗糙度为0.333 0 μm,ELID内圆磨削的表面粗糙度为0.596 7 μm,工件的表面粗糙度值降低了44.2%,有效提高了工件表面加工质量。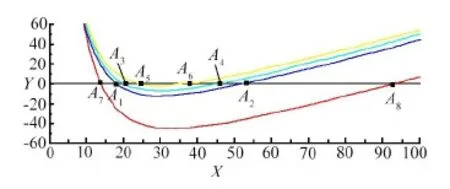
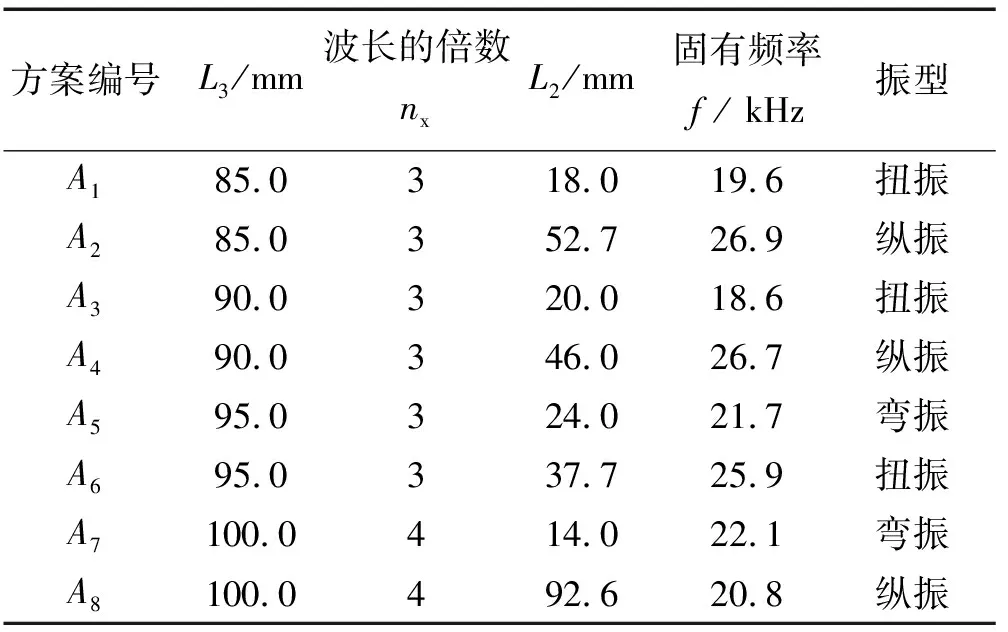
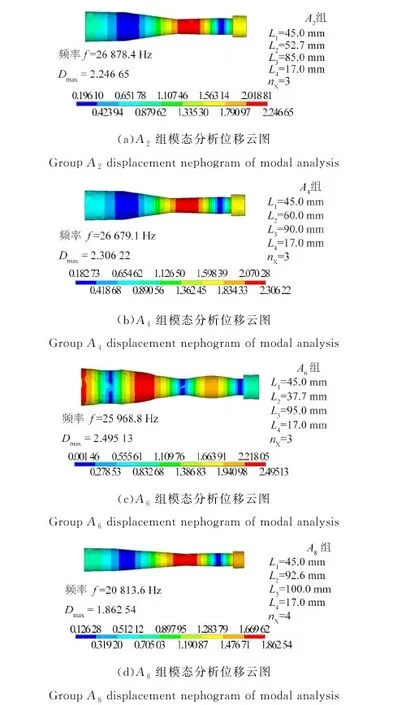
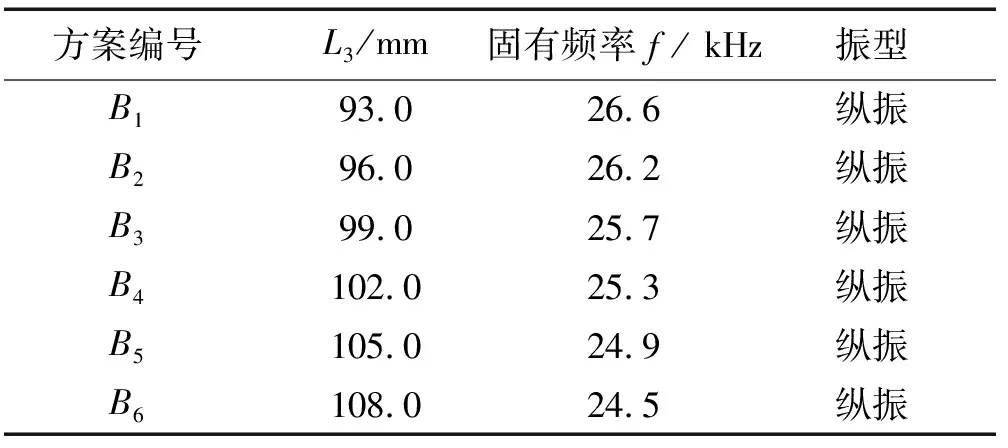
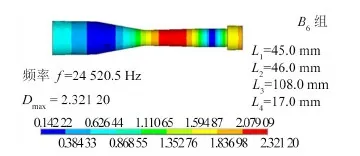
1.3 变幅器的有限元优化

2 具体试验测试
2.1 振动特性测试
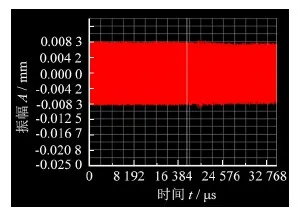
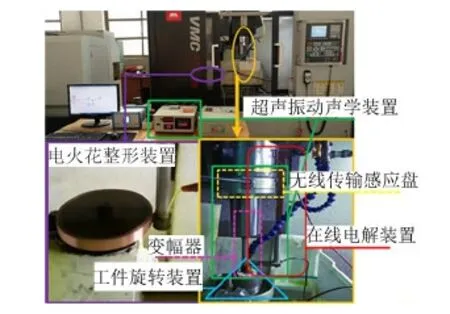
2.2加工特性测试


3 结论
