非理想条件下换能器阵列指向性研究

陈 敏，朱品朝，黄 平，朱 雯，刘 旺，曾 强

(1.电子科技大学 航空航天学院，四川 成都 611731；2.四川成焊宝玛焊接装备工程有限公司，四川 成都 610052)

0 引言

近年来，以获取高指向性低频波为目的的声波定向技术受到了世界各国研究者的广泛关注。通过换能器组阵的方式可实现声波的高指向性传播，将声波传播到很远的距离外。然而针对换能器阵列的指向性研究多数是假设在理想条件下的，即换能器阵列单元器件性能完全一致，其振动幅值及相位稳定[1-4]。但实际工程中不可能达到这种理想状态，因此，研究换能器阵元性能不一致的非理想情况下的阵列指向性的变化规律，对其工程应用具有实际价值。本文以换能器平面阵列作为研究对象[5]，对换能器阵元器件的振动速度幅值和相位在一定范围内呈随机正态分布及泊松分布的情况下，利用仿真分析手段，揭示换能器阵列指向性的变化规律。

1 换能器平面阵列指向性理论建模

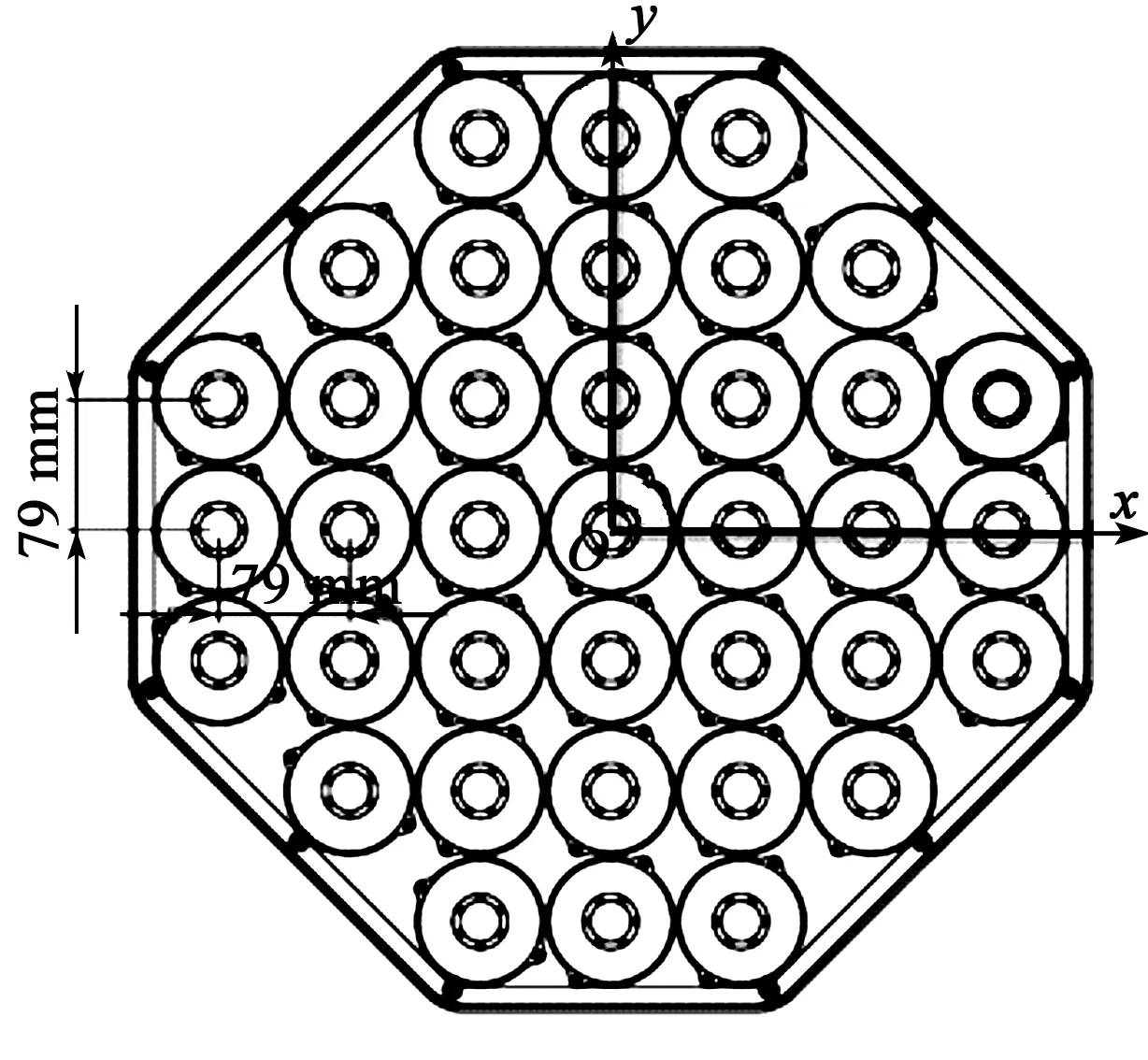
图1 声波定向驱散装置换能器阵

首先建立换能器阵的坐标系，取最中间一个换能器单元的位置为坐标原点O(0,0)，则整个八角形换能器平面阵列单元的位置排布坐标如表1所示。

表1 八角形换能器平面阵列单元位置坐标

如图2所示，换能器平面阵列所在平面为xOy平面。设声场中有一观察点P，其与坐标原点的距离为r，与z轴夹角为θ，旋转角为φ。P点的直角坐标可设为(x0,y0,z0)，P′为点P在xOy平面中的投影点。

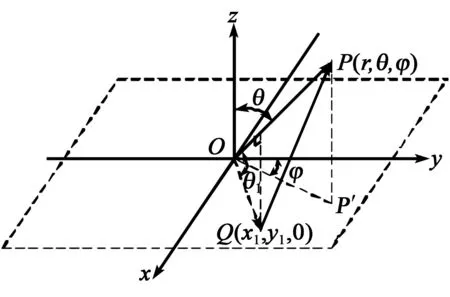
图2 换能器阵坐标系

(1)

式中：ρ0为媒质密度；k=2π/λ为波数,λ为声波波长；J1(x)为一阶贝塞尔函数。

同理可知，令换能器平面阵列中任意一个单元位于Q点，其到P点的声程为r1，则Q点处半径为a的换能器在P点产生的声压为

(2)

式中：θQ为QP与z轴的夹角[6]。

在远场时，可近似认为OP∥QP，OQ在OP上的投影为

PrjOPOQ=|OQ|cosθ1=rQcosθ1

(3)

式中：rQ为OQ的模;θ1为OQ与OP间的夹角。

由于P点和Q点的直角坐标分别为(x0,y0,z0)和(x1,y1, 0)，故OP、OQ可分别表示为{x0,y0,z0}、{x1,y1,0}。则式(3)中的夹角余弦为

(4)

式(4)中x0、y0转换为圆柱坐标,即

(5)

得

(6)

由式(3)、(6)可得声程r1与r的关系为

r1=r-PrjOPOQ=r-rQcosθ1=

|x1sinθsinφ+y1sinθcosφ|

(7)

在远场时，式(2)中振幅部分的r1≈r，θQ≈θ，则将式(7)代入式(2)可得换能器平面阵列中的任意一个单元(Q点)在远场P点处产生的声压为

ej(ωt+φ0-kr+k|x1sin θsin φ+y1sin θcos φ|)

(8)

ej(ωt+φi-kr+k|xisin θsin φ+yisin θcos φ|)

(9)

利用声波的叠加原理[8]，可推导出振动速度幅值和相位服从随机正态分布的情况下，圆形活塞换能器平面阵的指向性计算理论公式(泊松分布时推导过程类似)。根据式(9)可得换能器平面阵列在P点产生的声压为

ej(ωt-kr)ej(φi-k|xisin θsin φ+yisin θcos φ|)=

ej(φi-k|xisin θsin φ+yisin θcos φ|)

(10)

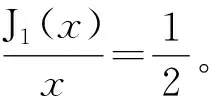
(11)

2 非理想情况下换能器阵指向性变化规律分析

2.1 振速幅值和相位对换能器阵列指向性的影响分析

将表1中换能器的坐标值代入式(11)可计算出不同频率下平面换能器阵列的指向性角，并分析在理想条件下与换能器单元振动速度幅值、相位服从正态分布条件下指向性的区别，根据某批换能器的参数，其振动速度幅值服从ui～N(2.1×10-3,(0.45×10-3)2)，相位大致服从φi～N(12.5,3.75)，声波频率(f)分别为1 kHz、2.5 kHz、4 kHz时的指向性结果如图3所示。表2为不同情况下换能器波束宽度。

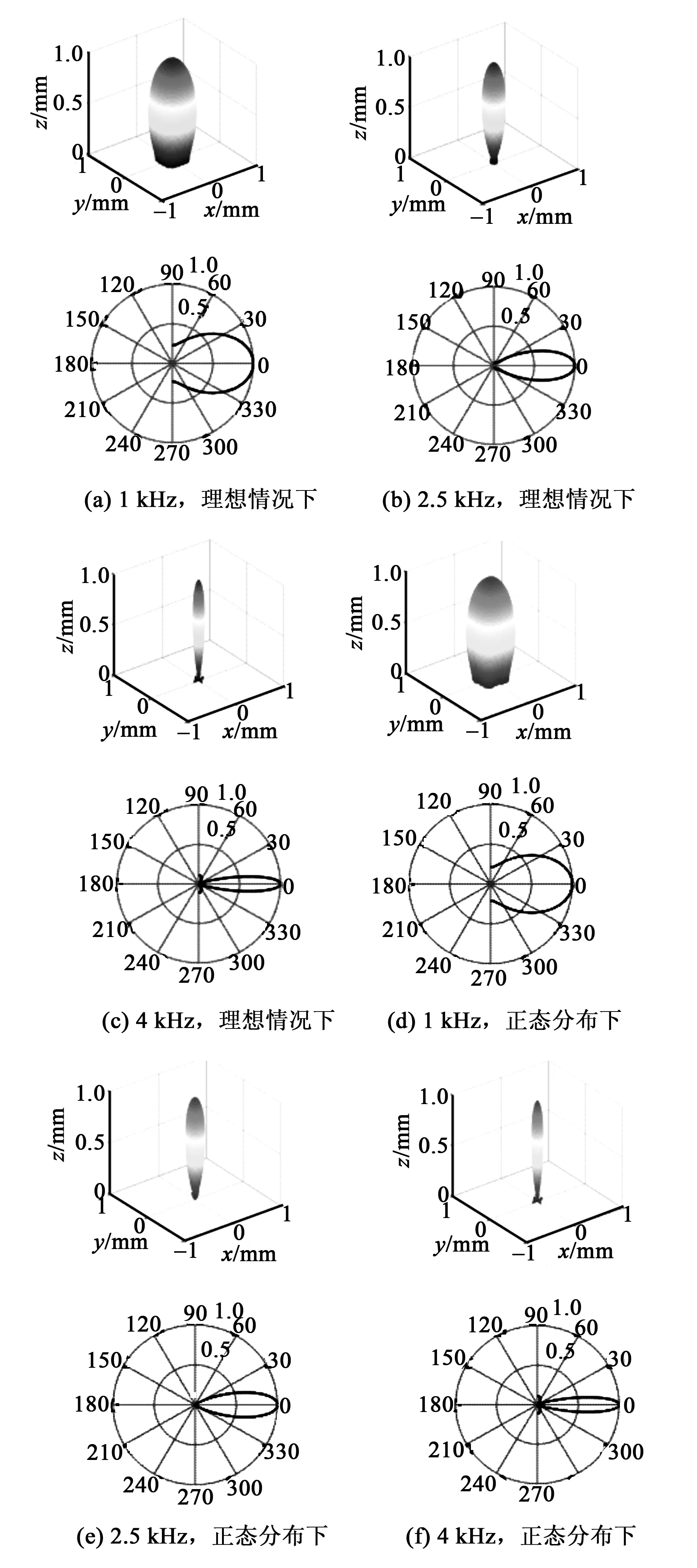
图3 不同情况下八角形平面换能器阵列指向性图

表2 不同情况下换能器波束宽度

波束宽度/(°)f=1 kHzf=2.5 kHzf=4 kHz理想情况下61.5123.5215.38正态分布下58.7924.4215.41

由图3、表2可知,随着f的增加，八角形平面换能器阵列指向性增强；频率继续增大时，指向性变得更好，但旁瓣更显著；当f增大到4 kHz时出现明显的旁瓣。与理想情况下的指向性相比，非理想情况下的指向性角整体呈振荡减小趋势，在1 kHz时，指向性角较理想情况下略小，在2.5 kHz时，指向性角较理想情况下略大，在4 kHz时，指向性角与理想情况下相差较小。此外，与理想情况下的指向性图相比，非理想情况下指向性图整体在频率较低时，其各个方向上指向性的对称性较差，如1 kHz时正态分布条件下，指向性角明显较大，阵列指向性图形状与理想条件下不同，但随着频率的增加，指向性图的形状差异逐渐变小，各个方向上的指向性近似相同。

图4为-3 dB波束宽度随频率变化曲线。由图可看出,随着频率的增大，波束宽度快速变窄，在f<2 kHz时波束宽度随频率变化明显；在f>2 kHz时波束宽度变化趋缓，在整体上仍呈下降趋势。非理想情况下与理想情况下波束宽度在频率越高时，其绝对误差越小，在f<5.5 kHz时，在0～10°内绝对误差波动；在f≥5.5 kHz时，二者的绝对误差趋近于0°，即在频率较高时换能器阵元间的不一致性对阵列指向性的影响较弱。

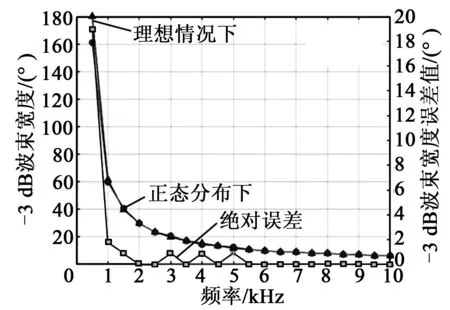
图4 -3 dB波束宽度随频率变化曲线

2.2 振速幅值离散度对指向性的影响

选择换能器阵列所发声波的f=2.5 kHz，分析换能器单元相位一定时，振速幅值的离散度对指向性的影响。在f=2.5 kHz的理想情况下，换能器阵列的-3 dB波束宽度为23.52°；当相位一定(在此令φ=12.5°)，对比振速幅值服从正态分布ui～N(2.1×10-3,σ2)与相同均值、方差下的泊松分布，在不同σ情况下，指向性角的均值与标准差(通过蒙特卡洛法，取200次仿真数据进行统计)变化趋势如图5所示。

图5 相位一定时，指向性角随速度振幅值标准差变化曲线

由图5可看出，在相位一定的情况下，泊松分布时，随着速度振幅标准差的不断增大，换能器平面阵列的指向性角的均值振荡变化，总体呈振荡上升趋势，指向性角的标准差呈明显的振荡增加趋势；而正态分布时，换能器平面阵列的指向性角的均值在σ<7.5×10-4或8×10-4<σ<12×10-4时稳定增加，并总体呈上升趋势，换能器平面阵列指向性角标准差呈现稳定增大趋势，并且明显小于泊松分布下指向性角标准差。总之，随着振动速度幅值离散度的增加，换能器平面阵列的指向性角呈增大趋势，指向性性能较理想条件下呈变差趋势。

2.3 相位离散度对指向性的影响

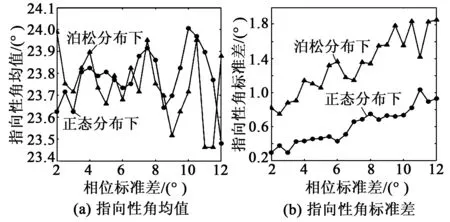
图6 振速幅值一定时，指向性角随相位标准差变化曲线

3 结论

本文通过对非理想条件下的换能器指向性理论计算模型的建立，采用仿真分析手段对非理想情况下换能器平面阵的指向性变化规律进行了研究，得到了以下结论：

1) 非理想情况下，换能器平面阵的指向性在频率较低时，受阵元的不一致性影响较大，频率较高时，影响较小；这种影响不仅体现在对三维指向性对称性的影响上，且也体现在对指向角指标的影响上，非理想情况下会使三维指向性图的对称性变差。

2) 理想情况下与非理想情况下的波束宽度的绝对误差在低频段时呈振荡变化趋势，但在频率较高时，换能器阵元的不一致性对波束宽度的影响较小。

3) 当换能器阵元间相位一致时，随着阵元振速幅值离散度的增大，阵列指向性角呈振荡增大趋势，在工程中应尽量选择阵元振速幅值离散度小的换能器制作阵列，以保证较小的指向角，获得良好的阵列指向性。

4) 随着阵元相位离散度的增加，阵列指向角总体上呈现振荡增大趋势，因此，在换能器工程制作中需尽可能提高设计和制作工艺，精确掌控换能器间的相位离散度，使其尽量小，从而保证换能器阵列获得较小的指向性角，指向性更佳。另外，根据这一特点可以为换能器阵列的指向性评估提供一个新的技术指标，并对实际工程应用中的换能器阵列指向性设计具有一定的指导意义。

5) 在非理想条件下，阵元的振速幅值及相位服从正态分布与泊松分布时，都会影响到换能器平面阵列的指向性，离散度越大影响就越明显；不同分布条件下的影响有差异，在工程应用中应该根据换能器阵元的具体差异有针对性地进行阵列指向性设计。

本文提出的非理想条件下换能器阵列指向性分析方法，一方面可以评估已购批次换能器做出的平面阵列的指向性性能，另一方面也可以为满足特定指向性要求的换能器阵列指向性设计计算出参数选择范围，通过该参数范围选择相应的换能器组成阵列就可以满足工程应用要求。对于大批量生产换能器阵列相关产品的厂家而言，通过这种换能器参数控制就可以生产出满足要求的换能器阵列，由此可解决此类企业生产质量控制的痛点问题。