基于RTD的三变量特征阈值逻辑门及通用阈值逻辑门设计
2020-03-12姚茂群冯杰王竹萍
姚茂群,冯杰,王竹萍
(杭州师范大学信息科学与工程学院,浙江杭州311121)
0 引言
共振隧穿二极管(resonant tunneling diode,RTD)是一种较成熟的非线性量子器件[1-2],具有负内阻(negative differential resistance,NDR)、开关转换速度快、低压低功耗、工作频率高等优点[3-4],且在数字电路设计中,使用器件数量更少。因此,RTD 具有很好的研究价值及应用前景[5-6]。MOBILE(MOno-stable BI-stable transition logic element,单双稳态转换逻辑单元)是基于RTD 设计电路时的一个重要逻辑单元[7-8]。MOBILE可以由2个或多个RTD 串联而成[9-11],其偏置电压为时钟信号,且MOBILE 在偏置电压为上升沿时工作。当偏置电压处于上升沿时,MOBILE中波峰电流最小的RTD 先进入负阻区,且该RTD 从低阻态变化到高阻态。当偏置电压为高电平时,MOBILE 能够保持输出不变。为了能有效控制MOBILE的输出,通常需要加入输入分支,如 RTD和HFET(heterojunction field-effect transistor,异质结场效应晶体管)的串联结构[10]。MOBILE 不仅充分发挥了RTD的NDR和快速开关转换特性,而且使得电路具有双稳态和自锁特性[9]。相比布尔逻辑,MOBILE 更适合设计阈值逻辑电路[11-13]。
三变量函数一共有256个,其中阈值函数104个,非阈值函数可以转化成几个阈值函数的相或[14],而由MOBILE 构成的阈值逻辑电路能实现三变量阈值函数,故该电路可以实现所有的三变量函数,但需要根据每个阈值函数的权值和阈值重新设计电路,电路设计过程复杂,缺乏通用性[15-16]。有关文献已设计了基于RTD 通用的三变量阈值逻辑门,但因在阈值或者正负权值的选取上不恰当,导致电路功耗增加、面积增大、成本上升[19-20]。本文结合MOBILE的特点,全面分析了三变量特征阈值函数和具有代表性的三变量阈值函数,设计了2种性能更好的三变量通用门电路。
1 理论基础
1.1 阈值逻辑
如果函数f(x1~xn)满足:存在一个称为权值的函数w1,w2,...wn的集合和一个阈值的数,当且仅当
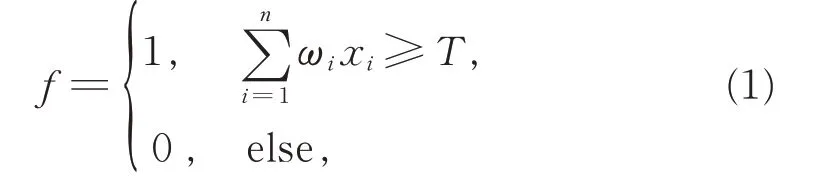
则称该函数为阈值函数[18],简记为f=〈ω1x1+ω2x2+…+ωn xn〉T,式中乘法及求和运算均为算术运算,其中xi∈{0,1}。对于一个变量输入,单变量输出的二值门电路,若存在一组权值w1,w2,…,wn和一个阈值T,使得该门电路输入输出关系可以用式(1)表示,则称该门电路为阈值逻辑门(threshold gates,TG)[17-18]。多个阈值逻辑门可以实现任意逻辑函数[18]。
基于MOBILE的RTD 阈值逻辑电路如图1所示[11]。由RTD和HFET的串联结构作为输入分支,控制MOBILE的输出,Vclk为时钟电压,wp0~wpn和wq0~wqn为RTD 面 积,xp1~xpn和xq1~xqn为输入变量(高电平为逻辑1,低电平为逻辑0),记与RTD 负载管并联的区域为NDR1,与RTD 驱动管并联的区域为NDR2。由于当RTD 电流密度一定时,RTD的面积与其波峰电流成正比,且HFET的作用类似一个开关,当栅极输入高电平时,HFET 导通;当栅极输入低电平时,HFET 截止。
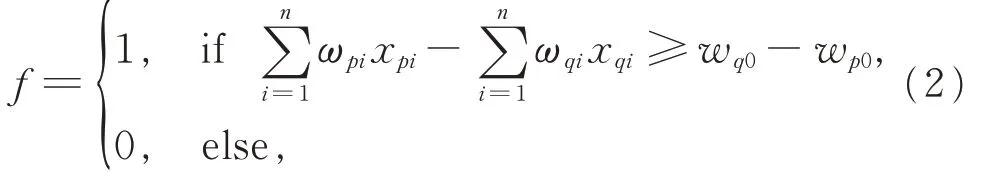
式(2)表示的正是阈值函数,且NDR1 区域中,输入变量的权值全为正,NDR2 区域中,输入变量的权值全为负,阈值表示向上取整。

图1 由MOBILE 构成的阈值逻辑电路Fig.1 Threshold logic circuit composed of MOBILE
1.2 谱技术
谱技术是一种数学变换方法。通过转换矩阵将传统布尔域{0,1}变换到谱域{1,-1},转换过程中无任何信息损失[18]。一个n变量函数f(x1~xn)有2n个不同的输入,对应2n个输出。定义输出向量Y=(f(+1,+1,…,+1),f(+1,+1,…,-1),…,f(-1,-1,…,-1))Τ,n阶Rademacher-Walsh谱域变换矩阵记为Tn,谱 系数向 量[r0r1...rn r12...r1...n]T记为R,则[18]

其中,r0为零次谱系数,ri为一次谱系数,rij为高次谱系数,谱系数为-2n~2n中的任意偶数,三阶Rademacher-Walsh 谱域变换矩阵为[18]

利用谱技术,不仅可以对函数进行分类,也可以判断其是否为阈值函数[18]。以三变量函数为例,通过将谱系数按绝对值从大到小排列,一共可分为3类,见表1。其中,|ri|表示零次及一次谱系数,|rij|表示二次谱系数。若最大值谱系数的绝对值8 或6出现在零次及一次谱系数上,或者零次及一次谱系数的绝对值出现3个4,则该三变量函数为阈值函数。三变量阈值函数的谱系数与权值的对照表如表2所示。表2中,阈值函数的|ri|按绝对值从大到小排列,对应的权值和阈值可以通过表2中的|ai|得到。
权值wi=ai,且ai极性与对应的ri相同;阈值T可由下式得到:

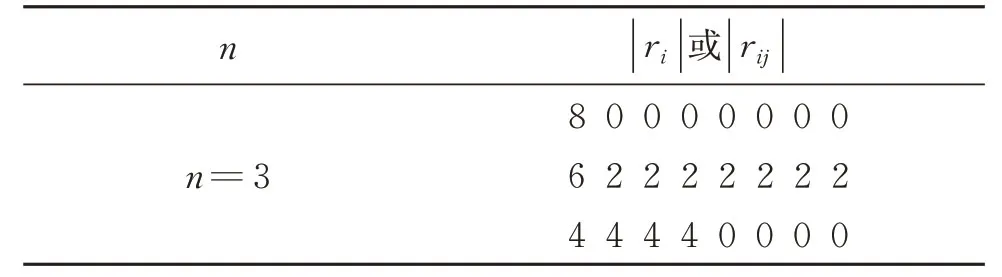
表1 三变量函数按谱数系数分类Table1 Classification of three-variable function according to spectral coefficients
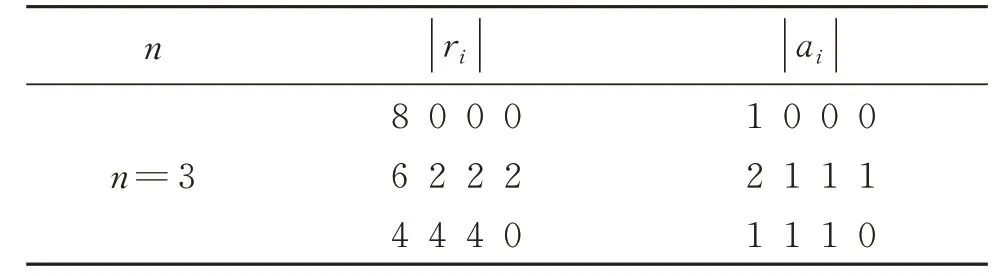
表2 三变量阈值函数的谱系数与权值对照表Table2 Look-up table about spectral coefficients and weights of three-variable threshold function
2 已有的工作
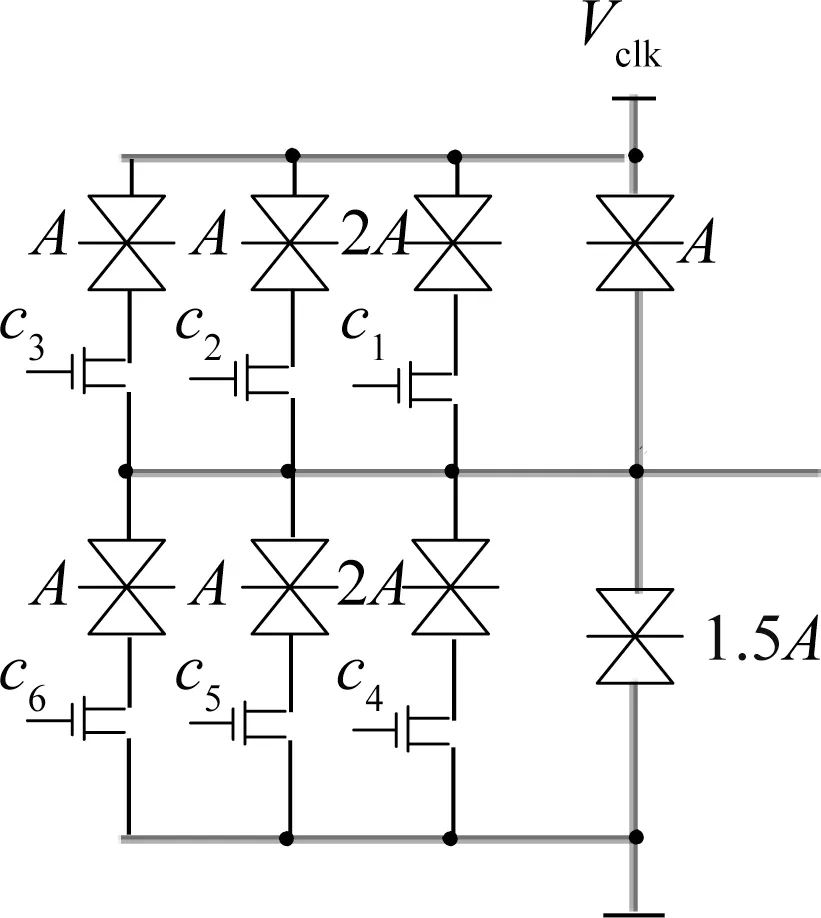
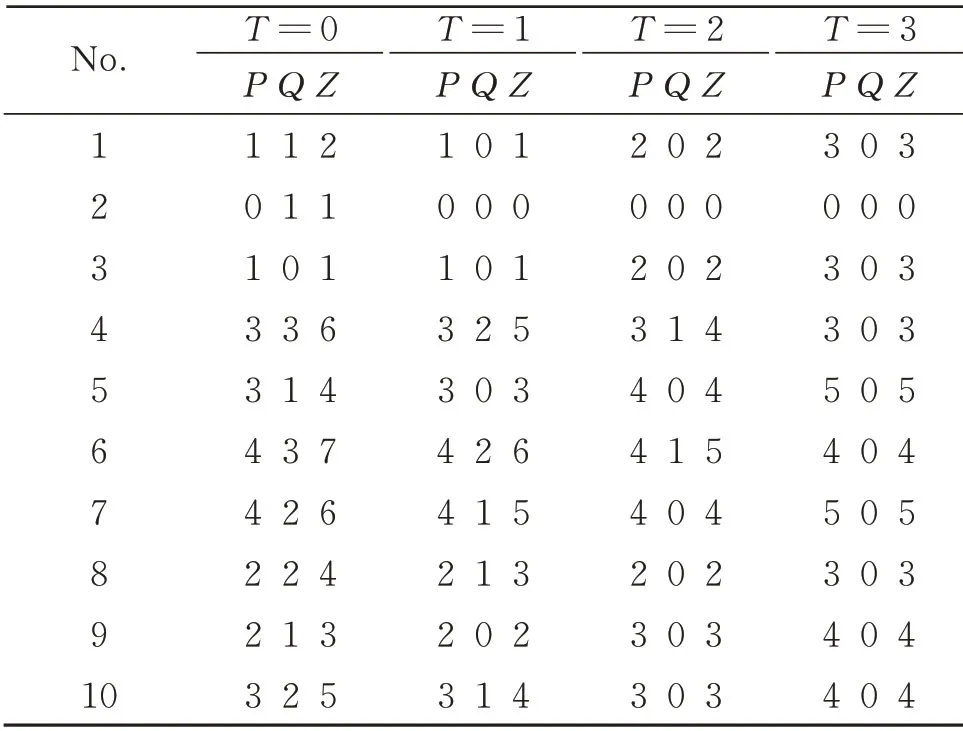
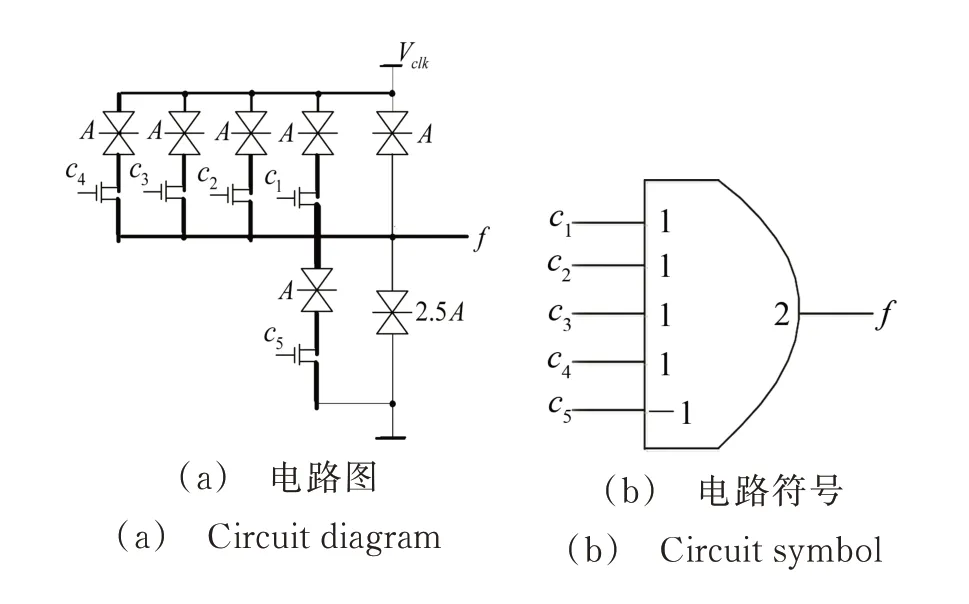
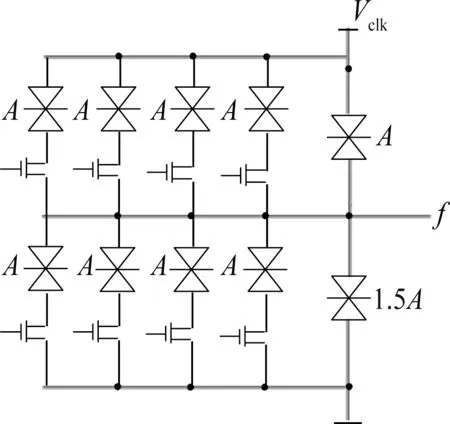
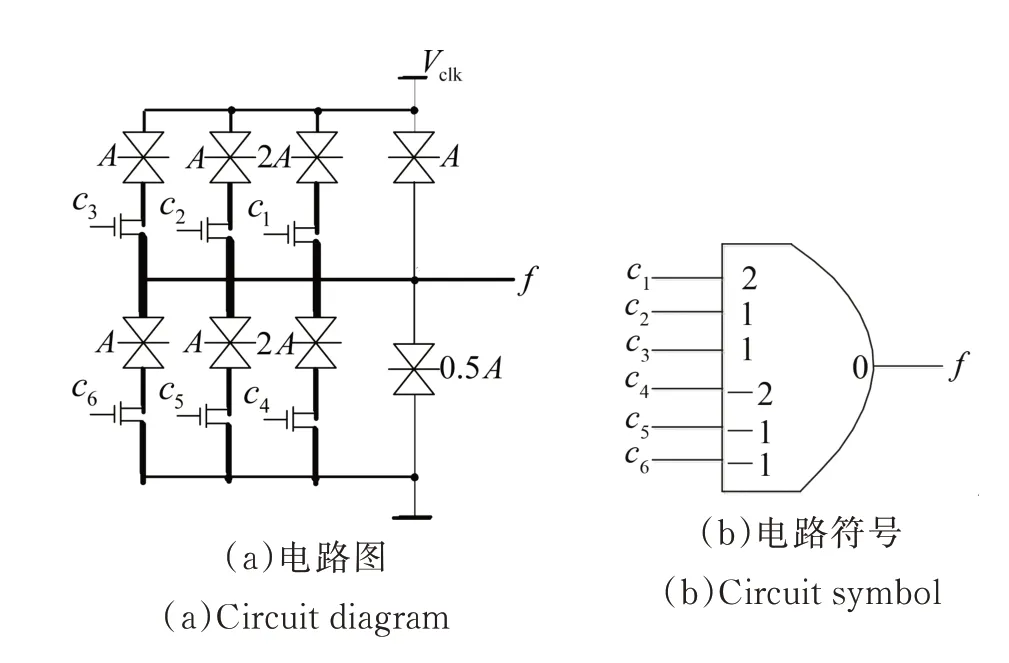
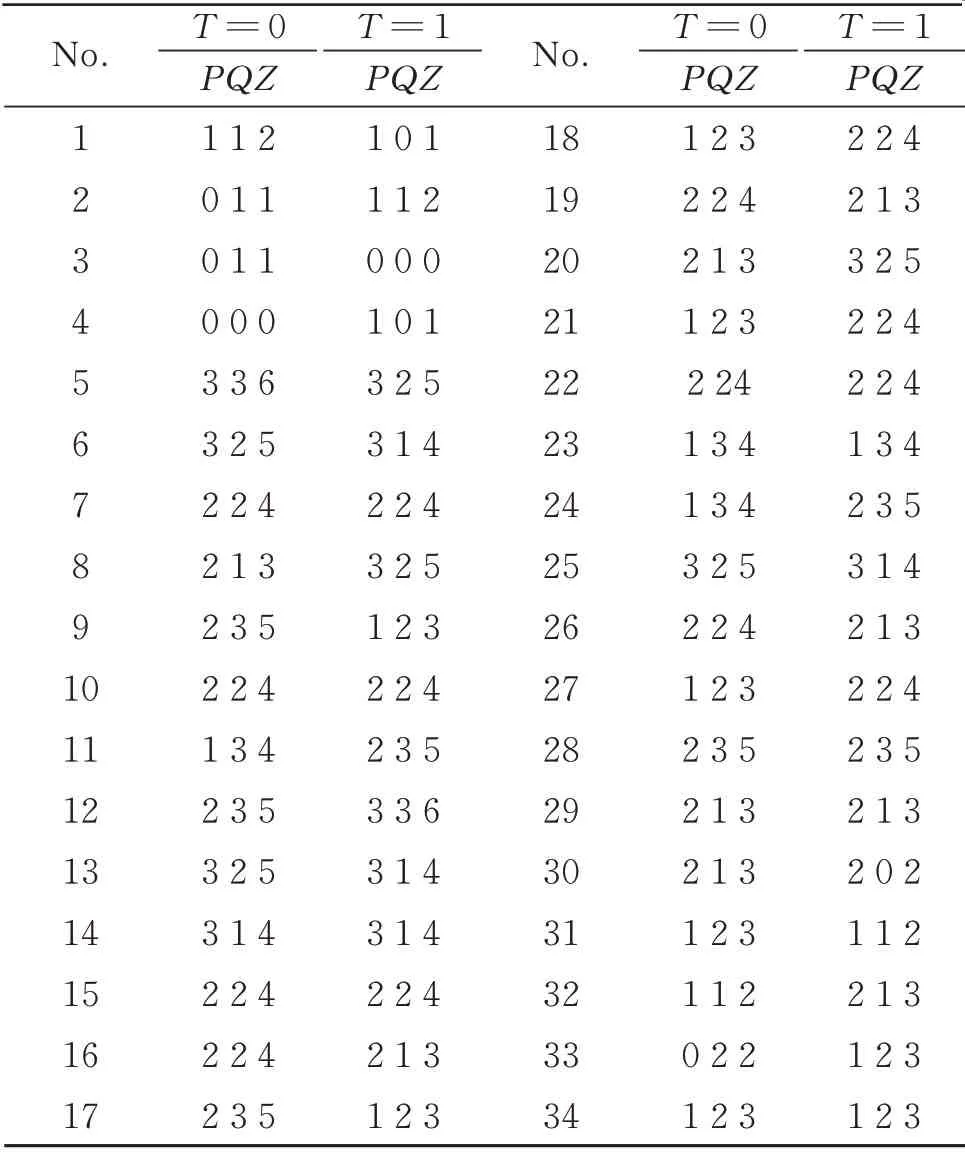
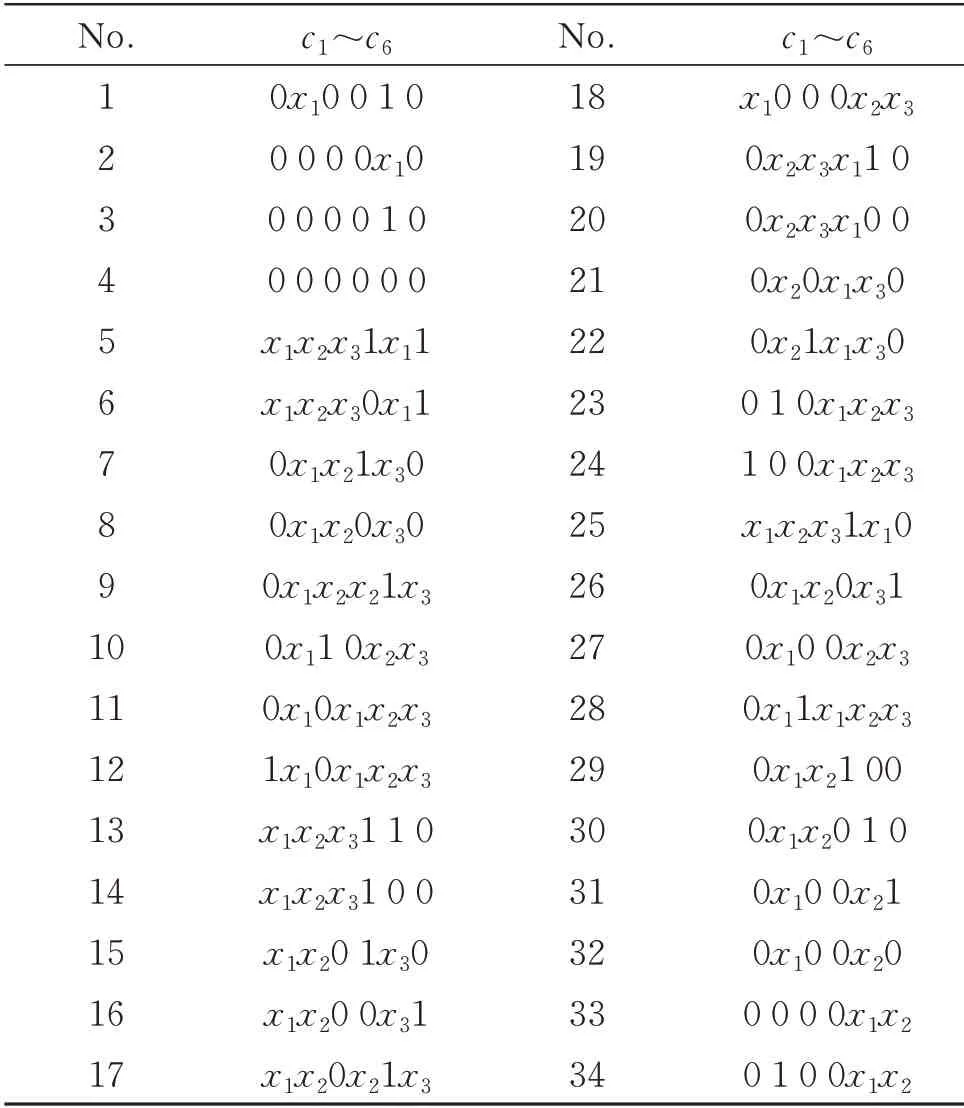
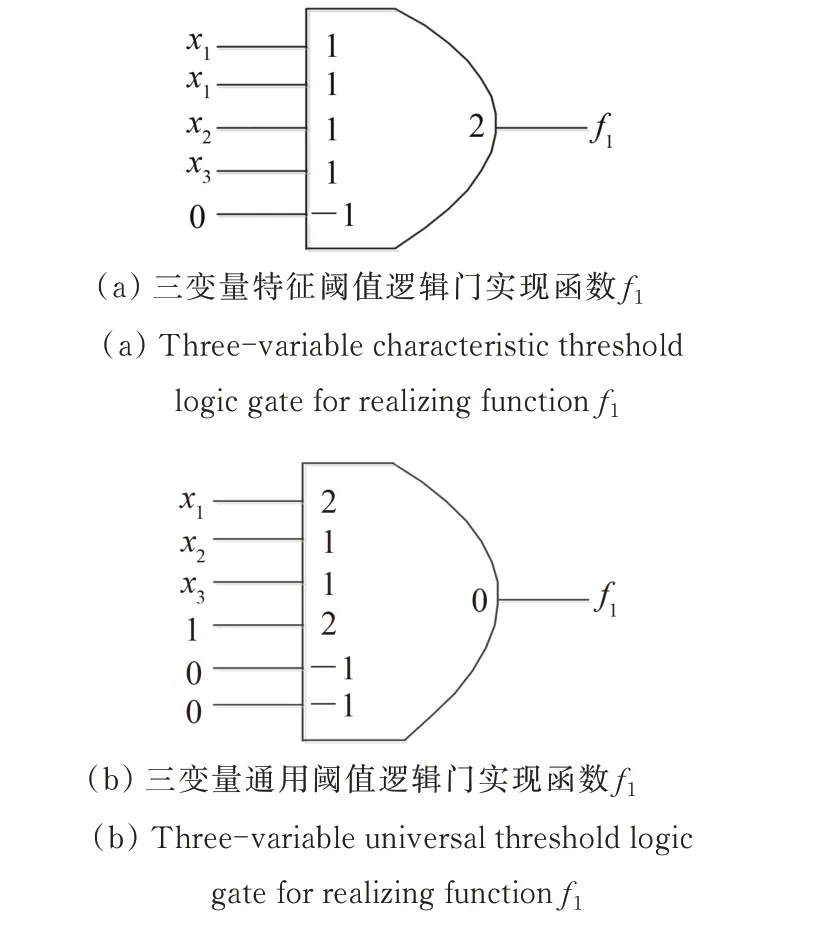
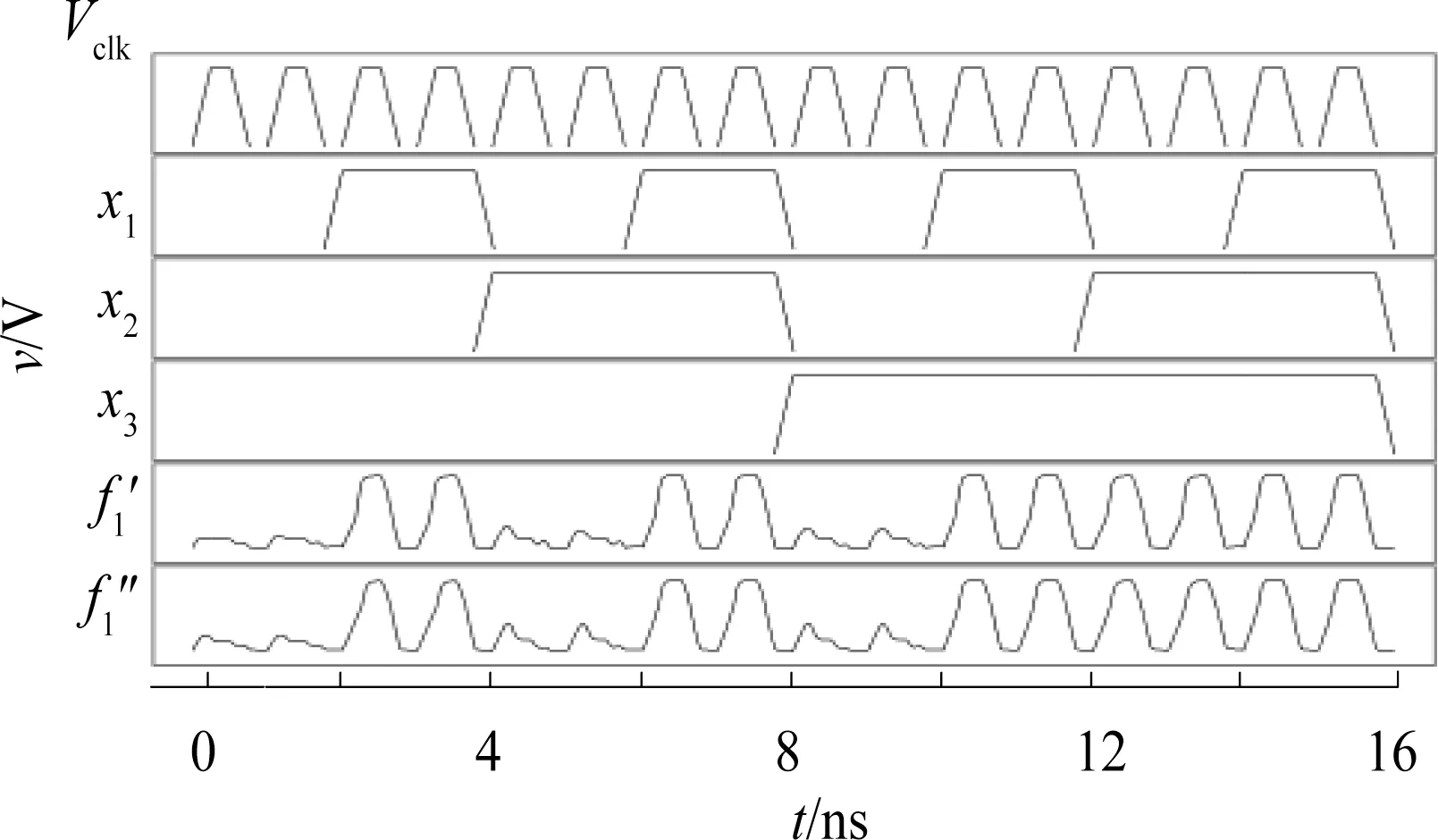
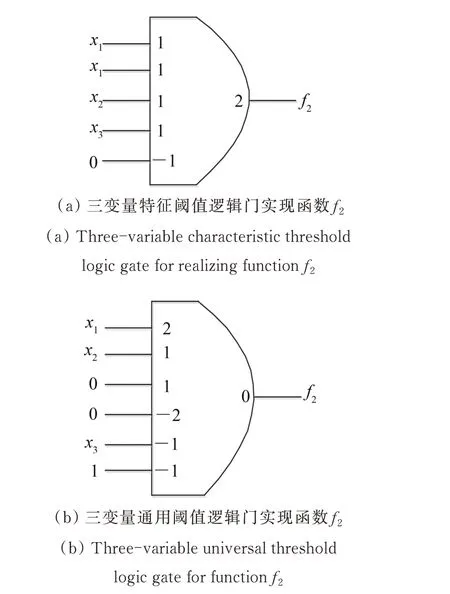
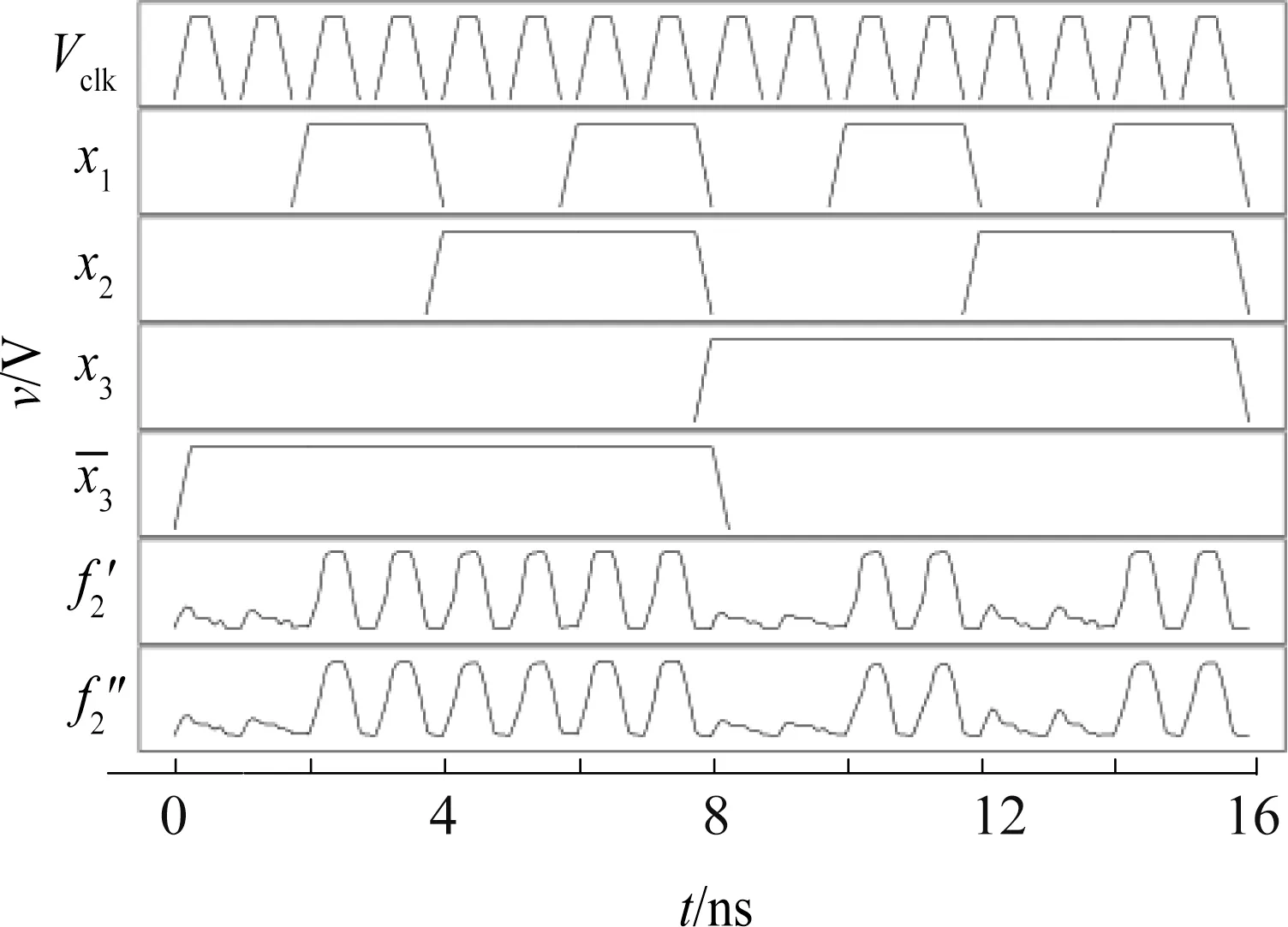
对于n变量的阈值函数,若其权值w1~wn全部大于等于0,且从大到小排列,即wi≥wj≥0,0 文献[20]选取权值为2,1,1的3个正权值输入端、权值为-2,-1,-1的3个负权值输入端和阈值为1的阈值逻辑电路作为三变量通用阈值逻辑门。如图3所示,通过不同的输入连接可实现所有的三变量阈值函数,其中c1~c6为6个输入端。 文献[19]设计的三变量特征阈值门非常简单,但其只考虑通过正权值输入端取高电平来改变电路的阈值,未考虑负权值输入端,导致电路选取的阈值较大。文献[20]设计的三变量通用阈值逻辑门对输入端权值的选取、正输入端数和负输入端数都很恰当,但对阈值的选取略显不足。 本文将分别研究三变量特征阈值函数及三变量通用阈值函数的谱系数,通过全面分析以上各简单可行的设计方案,设计出性能较好的三变量特征阈值逻辑门及三变量通用阈值逻辑门。 图2 文献[19]中的三变量特征阈值逻辑门Fig.2 Three-variable characteristic threshold logic gate in[19] 图3 文献[20]中的三变量通用阈值逻辑门Fig.3 Three-variable universal threshold logic gate in[20] 三变量函数一共有10个特征阈值函数,如表3所示。其中,零次及一次谱系数|ri|按绝对值从大到小排列。由于设计的是三变量特征阈值逻辑门,阈值逻辑电路的正权值输入端至少需要3个。表3中的权值为w1~w3,当阈值函数权值为2时,若阈值逻辑电路的正权值输入端权值只可取1,则可以通过2个正权值输入端输入相同变量解决;当阈值函数3个变量权值分别为1,1,1时,若阈值逻辑电路的正权值输入端权值只有3个,且为2,1,1,则可以通过负权值为-1的输入端输入相应变量解决;若阈值函数的阈值比阈值逻辑电路的大,则可通过权值为-1的负权值输入端取高电平解决;若阈值函数的阈值比阈值逻辑电路的小,则可通过权值为1的正权值输入端取高电平解决。因此,阈值逻辑电路的3个正权值输入端可分别取2,1,1 或1,1,1。又根据表3的阈值T,阈值逻辑电路的阈值可取0,1,2,3。当阈值逻辑电路的3个正权值输入端取2,1,1和1,1,1时,所需的正、负输入端数目分别如表4和表5所示,其中,P表示正权值输入端数,Q表示负权值输入端数,Z表示总输入端数。从表4和表5中可以看出,所需的总输入端数为5的有3个,分别为表4中阈值逻辑电路的阈值取2时和表5中阈值逻辑电路的阈值取2,3时,其余所需的总输入端数均超过5。由于输入端数的增加会使电路变复杂,故只考虑输入端数为5的3种情况。又由于当正权值输入端的权值取2时,所需的RTD 面积比权值取1时增加1倍,电路的功耗也相应增加,故表4中阈值取2的情况也不考虑。表5中阈值取3时即为文献[19]设计的三变量特征阈值逻辑门,若阈值选取太大,则会导致需要的RTD 面积增大,增加了电路的面积及功耗。因此,本文设计的三变量特征阈值逻辑门为表5中阈值取2的阈值逻辑电路,对应的电路图及电路符号如图4所示。表3中的c1~c5表示本文设计的三变量特征阈值逻辑门对于三变量特征阈值函数输入端的连接情况。 表3 三变量特征阈值函数Table3 Three variable characteristic threshold functions 表4 正权值为2,1,1时的正、负权值输入端数Table4 Number of positive and negative weight inputs when positive weights are 2,1,1 表5 正权值为1,1,1时的正、负权值输入端数Table5 Number of positive and negative weight inputs when positive weights are 2,1,1 所有三变量阈值函数经零次及一次谱系数变换,按绝对值从大到小可分为3类,若谱系数极性及对应的变量顺序不同,则三变量阈值函数就不同,需列出所有的三变量阈值函数。所有可能的三变量阈值函数共34个,如表6所示。 图4 所设计的三变量特征阈值逻辑门及其电路符号图Fig.4 Three-variable characteristic threshold logic gate designed and its circuit symbol 其他阈值函数可通过变量间的互换得到。由于表6中阈值函数的权值w1~w3出现了2,1,1和-2,-1,-1,一种简单想法是:阈值逻辑电路的正、负权值输入端都设计为4个,权值分别为1,1,1,1和-1,-1,-1,-1,且阈值为1,并将该电路作为三变量通用阈值逻辑门,见图5。 图5 一般的三变量通用阈值逻辑门Fig.5 General three-variable universal threshold logic gate 然而这种三变量通用阈值逻辑门没有考虑阈值函数的权值2和-2,使得电路输入端数较多。因此,最简单的阈值逻辑电路应该是3个正权值为2,1,1的输入端和3个负权值为-2,-1,-1的输入端,一共6个输入端。又由于表6中的函数阈值T在-2到3之间变化,若阈值逻辑电路的阈值取-2、-1,2,3,会因输入端数不够,无法实现某些阈值函数,如阈值取-1,则表6中编号为5的阈值函数无法实现。因此,选择0和1 作为其阈值。当阈值逻辑电路的正、负权值输入端个数都为3,且权值分别为2,1,1和―2,-1,-1时,若取电路阈值T分别为0和1,则所需的正、负输入端数目如表7所示。其中,P表示正权值输入端数,Q表示负权值输入端数,Z表示总输入端数。从表7中可以看出,无论阈值逻辑电路的阈值T取0 还是1,均能实现所有的三变量阈值函数。文献[20]设计的三变量通用阈值逻辑门正是表7中阈值为1的电路,但若阈值取为0,则可减少所需的RTD 面积,从而一定程度降低成本和功耗。故本文设计的三变量通用阈值逻辑门为 表6 三变量阈值函数Table6 Three-variable threshold functions 图6 所设计的三变量通用阈值逻辑门及其电路符号图Fig.6 Three-variable universal threshold logic gate designed and its circuit symbol 表7 当阈值T为0和1时的正负输入端数Table7 Number of positive and negative inputs when the threshold T is 0 and 1 通过HSPICE 进行仿真,采用文献[4]中介绍的RTD模型,其中RTD 波峰电压为0.28 V,波峰电流密度为9 kA·cm-2,电容为4 fF·µm-2,单位面积A为2 μm2,与RTD 负载管并联的HFET 采用耗尽型晶体管,与RTD 驱动管并联的HFET 采用增强型晶体管,阈值电压分别为-0.1 V和0.4 V,偏置电压Vclk采用时钟电平,幅值0.8 V,频率1 GHz,输入信号高电平取0.8 V,低电平取0 V。下面通过2个三变量函数进行仿真。 表8 输入端接法Table8 Connection method of input terminal 首先计算该函数的谱系数。由式(3)可得:r0,r1,r2,r3,r12,r13,r23,r123分别为-2,6,2,2,2,2,-2,-2。由表2可得函数的阈值逻辑表达式为f1(x1,x2,x3)=2x1+x2+x32。由表3,其对应的由三变量特征阈值逻辑门实现的电路如图7(a)所示。由表8,其对应的由三变量通用阈值逻辑门实现的电路如图7(b)所示。对图7电路进行HSPICE 仿真,仿真结果如图8所示,其中f1'表示由三变量特征阈值逻辑门实现的电路仿真结果,f1''表示由三变量通用阈值逻辑门实现的电路仿真结果。从图8中可以看出,本文设计的三变量特征阈值逻辑门和三变量通用阈值逻辑门都能实现正确的逻辑功能。 按照函数f1求阈值函数表达式的方法,可得f2(x1,x2,x3)=〈2x1+x2-x31〉,由于函数f2不是特征阈值函数,根据阈值函数性质: 图7 函数f1 实现电路Fig.7 Circuit for realizing function f1 图8 图7电路的HSPICE 仿真Fig.8 HSPICE simulation of the circuit in figure 7 因此,根据表3,其对应的由三变量特征阈值逻辑门实现的电路如图9(a)所示。根据表8,其对应的由三变量通用阈值逻辑门实现的电路如图9(b)所示。对图9电路进行HSPICE 仿真,仿真结果如图10所示,其中f2'表示由三变量特征阈值逻辑门实现的电路仿真结果,f2''表示由三变量通用阈值逻辑门实现的电路仿真结果。从图10中可以看出,本文设计的三变量特征阈值逻辑门和三变量通用阈值逻辑门均能实现正确的逻辑功能。 图9 f2 实现函数电路Fig.9 Circuit for realizing function f2 图10 图9电路的HSPICE 仿真Fig.10 HSPICE simulation of the circuit in figure 9 对三变量特征阈值逻辑门及通用阈值逻辑门的功耗进行了测试,并与文献[19]中的三变量特征阈值逻辑门和文献[20]中的三变量通用阈值逻辑门进行了比较,结果如表9和表10 所示。表9中,Z1和Z2分别表示在采用文献[19]和本文设计的三变量特征阈值逻辑门时除输入0 电平外的其他输入端总数,表10中,Z3和Z4分别表示 在采用文献[20]和本文设计的三变量通用阈值逻辑门时除输入0 电平外的其他输入端总数。从表9中可以看出,对于三变量特征阈值逻辑门,三变量特征阈值函数中Z1 表9 三变量特征阈值逻辑门功耗比较Table9 Power consumption comparison of three-variable characteristic threshold logic gate 表10 三变量通用阈值逻辑门功耗比较Table10 Power consumption comparison of three-variable universal threshold logic gate 通过谱技术及阈值逻辑电路,设计了一种新型的基于RTD的三变量特征阈值逻辑门及三变量通用阈值逻辑门。通过2个具体函数的HSPICE 仿真,证明了电路逻辑功能的正确性。在功耗测试中,有针对性地测试了几组阈值函数,测试结果表明,相比文献[19-20],本文设计的电路能有效降低电路功耗,电路面积和成本也得到了降低。本文使用由RTD 组成的MOBILE 来设计阈值逻辑电路,不仅因为RTD 作为量子器件较传统CMOS 工作频率高、功耗低,而且通过改变MOBILE的输入分支,能很方便地设计出阈值逻辑电路。当然,本文设计的三变量特征阈值逻辑门及三变量通用阈值逻辑门也可由其他器件组成。
3 三变量特征阈值逻辑门及三变量通用阈值逻辑门设计
3.1 三变量特征阈值逻辑门设计


3.2 三变量通用阈值逻辑门设计

4 仿真及分析
4.1 函数f1(x1,x2,x3)=x1+x2 x3
4.2 函数
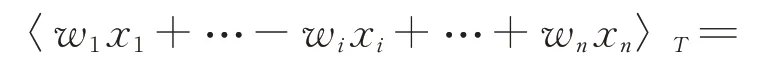



5 总 结
