基于排名学习和多源信息的地图匹配方法

卢家品，罗月童*，黄兆嵩，张延孔，陈为

（1.合肥工业大学 计算机与信息学院,安徽合肥230601；2.浙江大学 计算机科学与技术学院,浙江 杭州310058）

全球定位系统(global positioning system,GPS)，利用多颗定位卫星发射的定位信号,在全球范围内提供实时定位服务。近年来，越来越多的移动设备装有GPS模块,产生了海量的GPS 轨迹数据。这些数据不仅能提供诸如导航、重要目标定位等基于地理位置的服务，而且还能用于基于可视化、数据挖掘、机器学习技术的城市交通、人群流动及资源配给等问题的研究[1]。GPS 轨迹数据和地图数据的准确匹配是开展上述服务和研究的重要前提，但由于存在误差，两者间并不能准确匹配。主要误差有:(1)测量误差，传感器固有特性导致的测量误差；(2)采样误差，由于受流量及设备功耗等限制[2],出现低频、变频的GPS数据，而低频GPS数据将导致GPS点的间隔过大,无法有效确定它们之间的轨迹；(3)地图误差，由于测绘的不准确、不及时,造成一些地图数据与实际地形不完全相符[3]。

地图匹配(map matching)是对齐观察到的用户定位序列和数字地图上路网的过程。是最重要的GPS 轨迹数据预处理步骤之一[4]。地图匹配中，假设车辆或人只在道路上行走,所有道路之外的GPS数据点是不准确的,需要将其匹配到道路上。由于存在平行道路、隧道、Y 型道路等复杂地形[5]，简单地将GPS数据点映射到最近道路的做法常常会失效，对此有大量研究，相关方法可分两大类:(1)构建更合理的数学模型或理论模型来解决地图匹配问题;(2)结合其他数据解决地图匹配问题。这两类方法都取得了较好效果,所用理论模型也与数据类型和（或）应用场景密切相关。在面对高度数据[5]、基站数据[6]、陀螺仪、加速计[7]等新传感器,行人[7]、机器人导航[8]等新应用场景提供的新数据时，需要重新分析数据的特点,建立相应的数学模型，使得目前绝大多数地图匹配方法只对特定的数据和场景有效,无法灵活地应用到新的数据或场景中。

实际上,数据的变化并未改变地图匹配方法的本质,即地图匹配是利用环境数据和GPS 轨迹数据的时空特征,将GPS数据点映射到离散的路网数据的方法。因此,笔者从机器学习的思路,提出了一种基于排名学习(ranking learning)和深度神经网络(deep neural networks)的数据驱动的地图匹配方法,以解决多源信息融合的地图匹配问题。基于深度神经网络通过排名学习的方法，从已获取真实位置的GPS数据中有监督地学习评分道路与GPS数据点相关度的评分函数；再利用评分函数对所有可能的道路与GPS数据的相关性进行评分,选择评分最高的道路作为匹配结果。

通过学习评分函数来确定计算模型,隐式地使用数据的几何特征、拓扑特征、概率特征及轨迹的时空关系来完成地图匹配,而非事先定义的计算公式。因此，本方法可用于特定类型数据及拓展数据的情形。本文的主要贡献包括:（1）设计了一个数据驱动的地图匹配框架；（2）基于RankNet 设计了适用于地图匹配任务的排名学习方法；（3）设计了用于学习道路评分函数的神经网络；（4）提出了一种GPS 轨迹数据标注方法；（5）通过公开数据集,验证了方法的有效性。

1 相关工作

1.1 地图匹配

目前地图匹配的研究大致可分为2种:特定数据来源下，引入新的数学模型或理论模型；引入其他数据解决地图匹配问题。

引入新理论方法，依据所用的模型及理论可分为基于几何特征、拓扑特征、概率论和高级技术等方法[5]。基于几何特征的方法，利用点线距离、Fréchet距离、行驶方向与道路方向的夹角等几何特征,确定GPS数据所对应的道路[9-10]。基于拓扑特征的方法，将路网抽象成图等拓扑结构，实现地图匹配[11]。概率法，运用历史数据或专家知识建立概率模型,来判断GPS数据的对应道路[12]。高级技术法[13-15]，在数据的几何、拓扑、概率法的基础上建立运算模型,如机器学习模型,通过这些模型，综合数据的几何、拓扑、概率特征得到地图匹配的结果。常用的高级技术包括贝叶斯理论[12]、模糊理论[16]、隐马尔科夫模型(hidden Markov model,HMM)[13-14,17]、蚁群算法[15]等。此外,根据实时性,现有的地图匹配方法还可分为局部方法和全局方法。局部方法[16,18-19]，利用轨迹中几个GPS数据点完成匹配，具有实时性；全局匹配方法[10,13,15]，利用整条轨迹的数据点完成匹配，不具实时性。本文提出的属于局部方法。

引入其他相关数据能显著提高地图匹配的精度，如行驶速度和行驶方向数据[13,19]。HU 等[8]引入了历史行驶速度、周围道路行驶速度等数据；QUDDUS 等[5]则引入了高度数据、水平位置精度因子等数据；对比相关研究[13-14,17]发现，利用丰富的数据较单纯使用复杂的计算理论或模型更能大幅度提高地图匹配的准确率。但引入新的数据需要开展大量的数据建模工作,同时对数据的完整性有一定的要求[14]，这也限制了可应用的数据范围。本文提出的机器学习方法解决了该问题。

数据驱动的地图匹配研究相对较少，ZHENG等[20]从历史轨迹数据中挖掘轨迹模式,并用挖掘的轨迹模式来消除GPS数据的采样误差；GOH 等[21]提出使用SVM 学习一个函数,根据数据的几何度量和动量变化度量输出候选道路的传输概率,再用HMM 综合多种概率以获得最终的匹配结果。然而,所有这些方法都不能直接从数据中学习地图匹配规则,需要建立一定的数学模型,难以解决信息融合的地图匹配问题。

1.2 神经网络和排名学习

基于几何、拓扑、粗糙集的地图匹配方法表明，GPS数据与路网之间的关系可能由一个并不复杂的、难以确定具体表达式的函数确定，深度学习是解决这类问题的重要方法[22]。然而地图匹配问题和深度学习解决的问题并不相似，深度学习解决的基本问题是分类和回归。分类时，将一条道路判断为匹配结果，会影响对另一条道路是否为匹配结果的判断,因此，不能简单地用分类的思路解决地图匹配问题。回归问题的输出为连续量，而地图匹配的输出是对应道路的编号，是一个离散量，因而无法简单地使用回归解决地图匹配问题。借鉴信息检索的思路，引入排名学习以解决连续变量到离散变量的映射问题。

排名学习是从数据中学习数据排名规则的过程[23]。根据每次学习用到的数据类型，排名学习方法可分为3类:单独学习(pointwise)、成对学习(pair-wise)、列表学习(listwise)。已知数据的相关性评分时，可使用单独学习法，如McRank[23]，直接从数据中学习相关性的评分规则。当无法获取数据的具体评分，只能获取数据的优劣比较时，可用成对学习法，如RankNet[24]、Lambda Rank[25]，训练一个数据优劣的判断器，间接学习评分规则。当已知每次查询的所有数据的排名时，可使用列表学习法，如ListNet[26]，学习一个排名列表生成器。本文选择使用成对学习的排名学习方法。

2 相关定义及数据表示

图1为地图匹配问题示意图，所示为莫斯科，比例尺为1:15 000，绿线表示路网，红点表示未经处理的GPS数据，蓝线表示车辆的实际路径。为便于说明，对问题涉及的数据和地图匹配问题做形式化的定义。

定义1每条GPS 轨迹数据由一系列的GPS数据点构成,表示为T:p1→p2→…→pn，其中，pi=(xi,ti,ai)，xi表示GPS数据pi的经纬度，ti表示GPS数据pi的采样时间，ai表示该时刻下的其他数据(如速度)。2个相邻的GPS数据之间的时间间隔由GPS 接收设备的采样间隔Δt=ti+1-ti决定。

图1 地图匹配问题示例Fig.1 Map-matching example

定义2路网可以表示为一个有向图G(V,E)，其中V表示所有路段的起点和终点的集合，E={Vi®Vj|Vi,VjÎV}表示路网中所有路段的集合。

图2所示为位于德国海德堡市的霍根海姆的路网，比例尺为1:30 000。

定义3一条数字路径是指完全由路网中的边组成的路径，可表示为M:e1→e2→…→en，其中eiÎE。

定义4地图匹配是将GPS 轨迹数据T映射到路网，并找到对应的数字路径的过程。

图2 霍格海姆路网Fig.2 The road network of Hockenheim

3 基于排名学习的地图匹配方法

方法框架如图3所示，由以下3 步组成:

（1）候选道路选择。首先搜索GPS数据点的所有可能道路，以使排名网络只需对有限的数据进行评分，降低问题的复杂度。

图3 基于排名学习的地图匹配方法Fig.3 The pipeline of our method

（2）候选道路评分。使用学习所得评分函数对所有候选道路进行相关度评分。评分网络先逐层提取路网和轨迹的时空特征，再根据提取的特征对候选道路进行评分。

（3）选择匹配结果。选择所有候选道路中相关度评分最高的道路作为匹配结果，并将前一个结果到当前结果的最短路径作为数字路径。

3.1 候选道路选择

在地图匹配任务中，路网数据往往很大，导致匹配问题的搜索空间很大。故应先剔除无关道路，减轻计算负担。文献[3]指出,GPS数据相对于真实位置偏差的距离近似服从正态分布，该分布可表示为

式(1)中，gti表示GPS数据点pi对应的真实位置，σ是正态分布的方差表示根据两坐标经纬度计算的大圆距离(great circle distance),即从pi出发沿着地球表面到gti的最短距离，详情可参看文献[27]。式(1)表明，当道路到pi的大圆距离很大时，该道路为真实位置所在道路的概率就很低，因此，可以将所有满足的道路作为候选道路，其中cij，表示pi在第j条道路上的投影，r为阈值，其值的影响见实验部分。

例如,对于某条轨迹的某GPS数据点piÎTk，有如图4所示情况，其中ej,j=1,2,…,5表示路网中的5 条道路，cj表示点pi到道路ej上距离最短的点，黑色虚线表示以pi为圆心、r为半径的圆。所有道路中，到pi的点线距离(如点pi到点c2、c3、c4的距离)或最小距离(如点pi到点c1、c5的距离)小于r的道路被选为候选道路。图4中，点c2、c3、c4、c5位于半径为r的虚线圆内，故将道路e2、e3、e4、e5作为候选道路。

由于经纬度坐标不能无失真地投影在二维空间中，因此用以下海伦公式计算GPS点到道路的距离：

图4 候选道路选择Fig.4 The selection of candidate roads

3.2 候选道路评分

地图匹配是从路网中选择GPS数据点所在道路的过程，此过程也可看成是对路网中所有道路的排名。在实际中，容易确定GPS数据对应的道路，即排名最高的道路，但难以获得所有道路的完整排名，也难以获得所有道路和GPS数据的相关性评分，因此，本文选择成对排名学习法中的RankNet[24]作为学习方法。未经处理的原始数据，如时序的经纬度数据、路段起止点的经纬度等不足以表达GPS和路网数据的时空特征，且会对后续排名学习的结果造成影响，因此，应先对其进行提炼。本文选择深度神经网络学习评分函数提炼数据特征，候选道路评分过程如图3第3个流程所示。

设pi为需要匹配的GPS数据点，则pi可用n维特征向量qiÎ Rn表示。设集合D为pi的候选道路集合，则任意D中的道路ej可表示为m维特征向量，即mjÎ Rm。实际中，可根据已有数据的类型、数据的时空特性来选择合适的原始数据作为特征向量。本文将在实验部分通过具体特征向量的选择来说明方法的有效性。

用深度神经网络通过排名学习法学习评分函数，该函数可输出D中每个道路与pi的相关性评分。设神经网络的输入为uj=(qi,mj)，则评分函数可表示为F:uj®R，其中，i为GPS数据点的编号，j为道路的编号。由文献[24]，用以下损失函数作为优化目标：

本文设计了图5中的神经网络，命名为评分网络。该网络借鉴了残差网络[28](ResNet)、实例正则化[29](instance normalization,IN)、ReLU[30]等结构的特点，使用全连接层 (fully connected neural networks,FC)来学习数据的多层表达。为了提高网络对非线性关系的拟合能力，采用深层神经网络，为避免出现随层数增加网络性能恶化的问题，同时增强了网络的学习能力，以加快收敛速度，降低训练所需数据量，本文在网络中增加了残差(residual)结构。当GPS数据量较少时,易发生梯度消失，导致训练不收敛，本文采用实例正则化[29]解决此问题,实例正则化计算参见文献[30]。由于某一区域的经纬度数据仅在有限的几位数字上变动，对于所有输入神经网络的数据，本文将特征向量的每个分量的每位数单独作为一个输入单元。设输入向量的维数为din，则输入评分网络的数据可表示为

式(5)中，ujÎ Rdin,qi为GPS数据向量，mj为某条候选道路的向量表达。设隐层神经元数为dhid，则全连接层、ReLU层、IN层、残差的复合函数为

式(6)中，hi为第i层神经网络的输出，当i为奇数时，残差resi-2为第i-2层网络的输出，否则为零。首层全连接层WÎ Rdin´dhid，中间各全连接层WÎ Rdhid´dhid，最后一层全连接层WÎ Rdhid´4。经 实验测试，设置评分网络的隐层数dhid=64。网络输出的评分通常为一常量，为使网络更易收敛，最后一层输出四维向量，用激活函数将各维数值约束在[0,1]内。按以下公式得到最后的评分：

式(7)中，Fj为最后一层输出向量的第j维分量。

3.3 评分网络的训练

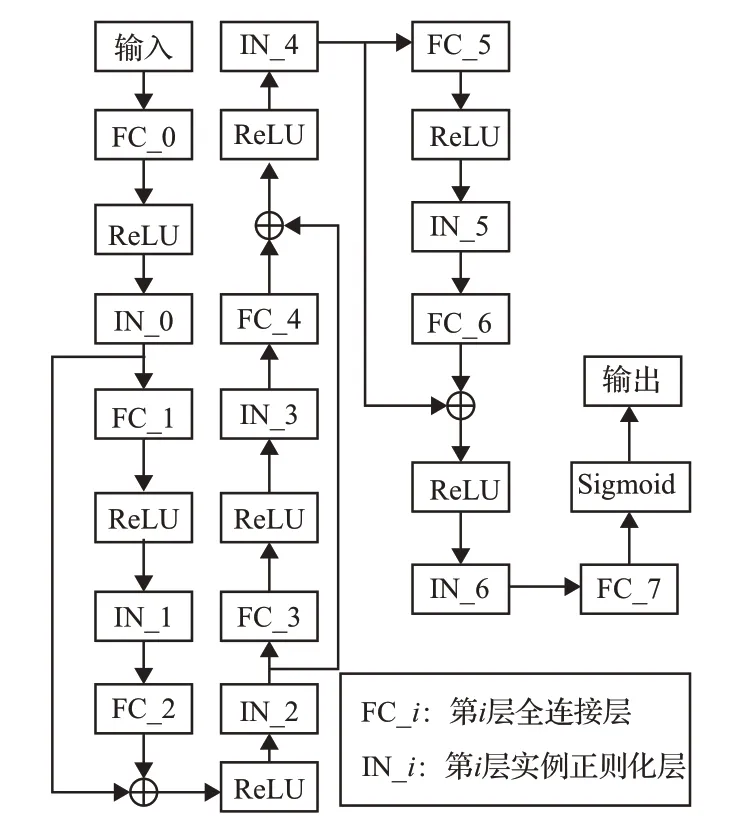
图5 评分网络结构Fig.5 The structure of scoring network

在使用评分网络前需要对其进行有监督的训练，训练过程如图6所示，其中，ui、uj的定义与式(4)同。每次训练时，输入ui与uj2个向量到评分网络，其中一个向量的分量m对应的道路为目标实际所在道路，另一个对应的为候选道路中的任意一条错误道路。评分网络分别输出2个向量的相关度评分，2个相关度评分相减得oij。为了完成有监督的神经网络训练过程，需要确定正负样本，本文采用以下做法标记数据:当ui对应的为目标实际所在道路时,则反之

图6 训练评分网络Fig.6 Training scoring network

训练步骤:

（1）对每一个GPS数据点生成候选道路集D；

（2）选取实际行驶的道路和D中任意一条非实际行驶的道路组成ui与uj对，其标签由本小节所述的标记方法确定；

（3）将数据按图6所示的结构进行计算，得到损失值；

（4）利用梯度下降法等优化方法更新评分网络的参数；

（5）对每个GPS点重复以上4 步,直至网络收敛。

当训练完成后，即可用评分函数对候选道路和轨迹上某一点的相关性进行评分，评分最高的那条候选道路为地图匹配结果。

3.4 算法复杂度分析

时间复杂度来自两部分，一部分是候选道路提取，另一部分是额外信息ai的计算和神经网络输出的计算。首先分析候选道路提取的算法复杂度。设某条GPS 轨迹有n个GPS数据点，对每个数据点需要遍历路网中所有道路来寻找候选道路。设路网中有l条道路，则候选道路提取的算法复杂度为O(nl)。接着再来分析另一部分的算法复杂度。总共有nk个候选道路，对于每条道路可能需要最短路径等额外信息，这部分的算法复杂度为O(llogl)。神经网络的计算复杂度是一个常量，因此第二部分的算法复杂度为O(nkllogl)，总的算法复杂度为O(nkllogl+nl)。若不计算最短路径，则算法复杂度为O(nk+nl)，而基于HMM的地图匹配方法的时间复杂度为O(nk2llogl)。因此，本文方法较该方法快了k倍，通常k值为20～200。

4 实验分析

为证明方法的有效性，将本文方法与目前公认的效果最好的地图匹配方法——基于HMM的地图匹配方法[13]、速度最快的地图匹配方法——基于夹角特征和基于距离特征的地图匹配方法[9]进行对比，分别从参数影响、信息融合、实际轨迹匹配结果三方面来说明。实验所用数据为文献[32]提供的验证地图匹配算法结果的公开数据，每次实验前，都会对照引文方法设置最佳参数。

4.1 数据说明

实验用数据来自莫斯科、霍普金斯、米兴多夫等20个不同的城市，每个城市有且仅有一条轨迹数据。实验数据包含平行道路、Y 型道路、环形道路、立交桥、城市道路、乡村道路等各类不同形状的道路。路网数据来自OpenStreetMap(OSM)提供的地图数据。所有轨迹数据均由真实的车辆搭载GPS设备采集而来。每条轨迹含有1 500～3 000个GPS数据点，采样间隔为1 s。为获取这些轨迹的数字路径，文献[32]采用人工标记方法标记出了目标的数字路径。路网数据如图7所示，由一系列首尾相连的线段组成的折线表示，每条线段有各自的编号。为便于检索，将路网数据中所有长度大于60 m的线段划分成数条小于60 m的线段。轨迹数据T是由一系列有序的数据点pi组成，每个数据点pi有3个属性:经度、纬度、记录时间，数字路径M :e1→e2→…→en由路网数据中一系列的路段编号组成，由于手工标记的标签无GPS数据点所对应的实际地理位置，只有数字路径，本文将数字路径中距离该GPS数据点最近的位置作为该GPS数据点的实际位置。选用pi的特征向量qi为轨迹中连续5个GPS数据点，即qi=(pi-2,pi-1,pi,pi+1,pi+2)，每个向量p带有的额外属性ai为时间戳，单位为m；选用某条候选道路上到pi的大圆距离最短的点作为该道路上的实际位置cj，候选道路的向量表示为mj=(A,B,cj,aj)。图7左所示的A、B分别表示候选道路投影点cj所在路段的起止点，aj表示道路行驶方向等额外属性。

图7 路网数据Fig.7 The data of road network

采用5 折检验法检验匹配方法的性能。该方法以城市为单位，选择所有城市中的80%及其中的轨迹为训练集，20%及其轨迹为验证集，训练集与验证集的轨迹、路网互不相交。

4.2 实验环境及评判标准

测试时使用的实验设备为Core i7-8550U,1.80 GHz的CPU;内存为8 GB，操作系统为Windows 10，开发语言为python，神经网络用pytorch 搭建。地图数据以geohash 索引的方式存储在redis数据库中，用lua 脚本语言实现快速检索。为保证算法运行结果的合理性，仅用lua 脚本实现数据的检索，神经网络、HMM 及粗糙逻辑均用python实现。

训练时,用Adadelta[33]优化评分网络，训练速度(learning rate)为0.1，batch size为80，rho为0.9，epsilon为10-6，使用L2 正则化项，大约迭代训练600次后收敛。这些超参数由优化算法的类型决定，不影响评分网络性能，训练耗时约1 h。若在GPU 下训练，将可大大缩短训练时间。

实验采用在地图匹配研究领域普遍使用的正确的段标识(correct segment identification，CSI)作为地图匹配方法准确率的评判标准，公式为

4.3 实验结果

4.3.1 搜索半径r的选择

参数r，即候选道路的搜索半径，需要人工调节。前文3.1节提到，GPS数据与其真实位置的距离服从以0为中心的正态分布。当r>3σ时，此时因搜索半径导致的准确率下降可忽略不计，而计算时间可显著减少。本实验所用数据σ=21.2 m，r与准确率和运行时间的关系如图8所示。随着搜索半径的增大，运行时间先缓慢再显著增长，准确率先显著再缓慢增长。当搜索半径r大于65 m时，随着搜索半径的继续增大，准确率不再显著提高。实际中可根据数据估计σ，选择合适的r来平衡计算时间和准确率。本文选择r=75。

4.3.2 信息融合

为验证本文方法在信息融合方面的表现及所设计的评分网络的有效性，将本文方法与MLP 方法做了对比；为验证本文方法能够有效融合新类型的数据，保持查询向量qi不变，在候选道路的向量表示mi的额外属性分量ai中依次增加道路行驶方向限制及上次匹配结果到该候选道路的最短路径距离，并以CSI 作为结果的度量标准，实验结果如表1所示。结果表明,本文提出的评分网络在地图匹配问题上较直接使用MLP的准确率更高。在面对新的数据时，本文方法无须重新设计新的算法，只需重新训练评分网络。结果显示，重新训练后准确率有显著提升。在不重新建模的前提下，当道路行驶方向缺失时，基于距离特征和夹角特征的方法，只能简单地删除与道路行驶方向相关的公式，导致准确率显著降低；当增加最短路径距离特征时，必须重新建模来确立新旧特征关系，否则无法利用新的特征。当缺失数据时，基于HMM 方法无法得到正确的结果。综上所述，本文方法可以通过重新训练建立新的计算关系，当数据缺失时，确保准确率不会显著降低；当引入新数据时，能有效利用新数据提高准确率。

表1 信息融合结果Table1 The result of information fusion

4.3.3 与其他方法的比较

采样频率与算法CIS有关，本文采用下采样法降低轨迹的采样频率以获取实验所需数据。为保证采样频率降低后点数不变，当采样频率降至原来的后，原轨迹也就被等分成了n个子轨迹，轨迹总数增大为原来的n倍，总的GPS数据点数目不变。图9为各方法在不同采样间隔下CIS的变化情况，发现本文方法取得了与基于HMM的地图匹配方法相当的效果，同时本文方法无须HMM 方法所需的大量未来轨迹数据，具有实时性优势。当采样时间增大时，本文方法的基于最短路径数据的版本的准确率会收敛至无额外属性版本。

图9 CIS与采样间隔的关系Fig.9 The relationship between CIS and sampling period

GPS数据点数目与算法运行时间有关，图10为各方法在不同GPS数据点数目下的运行时间，从中可看出，本文方法相对基于隐马尔科夫模型方法在运算速度上具有显著优势，接近于基于夹角特征和基于距离特征的地图匹配方法，同时,本文的不基于最短路径属性版本在耗时上和基于夹角特征与基于距离特征的地图匹配方法相近。

图10 运行时间与轨迹点数的关系Fig.10 The relationship between run time and the number of points of a trajectory

5 结 语

提出了一种基于数据驱动思路的地图匹配方法，该方法将地图匹配问题转换为信息检索问题，并用排名学习和深度神经网络直接从数据中学习地图匹配规则，无须建立具体明确的计算表达式，可快速融合新数据，适合需要融合多源信息的地图匹配问题。实验表明，该方法易于融合新数据，在准确率方面接近目前最准确的地图匹配算法——基于HMM的地图匹配方法，且运行速度更快，运行时间接近基于夹角特征和基于距离特征的地图匹配方法。

当然，该方法仍有很多需要完善的方面。首先，没有从路网本身出发去学习需要的信息，而是把路网抽象成路段的向量表示；其次，没有完美解决两相邻GPS数据点之间的轨迹确定问题，目前采用的策略是默认相邻两位置之间的轨迹是最短路径。此外，该方法目前只用到了局部信息和增量信息，没有用到全局信息。未来将着手研究如何利用轨迹的全局特征来提高地图匹配的准确率。