一种基于主题时空价值的服务器端瓦片缓存算法

陆晔，张伟，李飞，杜震洪*，张丰，刘仁义

（1.浙江大学浙江省资源与环境信息系统重点实验室,浙江杭州310028；2.浙江大学地理信息科学研究所,浙江 杭州310027；3.山东省国土测绘院，山东 济南250102）

瓦片服务是WebGIS中最重要的功能之一，其出现改变了地理信息数据的发布与获取方式，为人们的生活体验和工作带来了便利。然而，随着GIS用户规模和各种影像产品瓦片数据量的持续增长，瓦片服务器面临服务过载和响应延迟等问题[1]。通过在客户端和瓦片服务器间添加瓦片缓存服务器的方法[2]，可以有效降低源瓦片服务器接受请求数目，提高瓦片的响应速度，而瓦片缓存算法的优劣则决定了瓦片缓存的命中率，直接影响缓存服务器的压力分流能力和WebGIS 用户的请求等待时间[1]。因此，瓦片服务器端缓存算法的相关研究，对于提升WebGIS服务质量具有重要意义。

国内外学者针对瓦片数据缓存算法做了较多研究，KANG 等[3]研究了瓦片的预取和替换方式，用预取概率高的瓦片替换转移概率最小的。王浩等[4]研究了基于瓦片寿命和访问热度的缓存置换算法（TCLEPR），通过瓦片缓存存活超限寿命和瓦片访问热度来计算瓦片老化程度，置换出老化程度最高的瓦片的缓存。涂振发等[5]研究了最小空间数据价值缓存置换算法（GDLVF）,通过数据访问时间、访问频率、数据大小和空间位置特性计算瓦片价值，置换出价值最低的瓦片的缓存。LI 等[6]研究了stat算法，用瓦片访问次数和访问时间间隔来累计瓦片的stat值，置换出stat值最低的瓦片的缓存。刘佳星等[1]研究了基于地理单元热度的瓦片缓存置换算法（GUH），通过瓦片所包含的地理单元和缩放层级来计算瓦片热度值，置换出热度值最低的瓦片的缓存。这些文献通过研究瓦片访问的时空局部性原理，定义了各自的瓦片价值（概率、老化程度、热度或stat值），根据价值来置换瓦片，这些方法较传统缓存置换算法获得了较好的效果，但在应用于服务器端瓦片缓存时存在2个问题：(1)面向单一类型瓦片数据的缓存算法，没有体现瓦片类型对于瓦片价值的影响，不太适合服务器端拥有大量不同类型瓦片数据的场景；(2)通过瓦片访问频率或地理单元热度来反映瓦片的空间局部性，仅仅反映了瓦片的长期空间局部性，缺乏对短期空间局部性的表现，即没有考虑当前请求瓦片对下一时刻其邻近位置瓦片被访问造成的影响。

本文在基于价值的瓦片缓存模型的基础上，提出了一种基于主题时空价值的服务器端缓存置换算法（GDTST）。相较于现有的瓦片缓存算法，进行了以下优化：(1)在考虑瓦片访问的时间局部性和空间局部性基础上，进一步引入了瓦片主题权重，并设计了基于主题金字塔的缓存索引，使其适应多类型瓦片的服务器端瓦片缓存；(2)优化了空间局部性的表达方式，通过计算基于瓦片邻接范围的空间访问频次，实现在考虑长期空间局部性的同时兼顾短期空间局部性。

1 基于主题金字塔的瓦片缓存索引设计

瓦片数据是由影像或地图数据按照某种瓦片数据模型切分而成的数据单元，目前常用的瓦片数据模型为金字塔模型。瓦片金字塔模型是一种多分辨率的层次模型，它先将影像或地图数据按“行×列”的方式进行切片，生成瓦片矩阵，再通过分级、分块构建多尺度瓦片矩阵集[7]。在单个瓦片金字塔中，每一张瓦片都可以通过层级、行号与列号唯一确定。然而，瓦片服务器往往提供多套瓦片数据的访问，原有的仅依靠层级与行列号的缓存索引体系[1,4,8]已经不再适用。因此，为了在服务器端缓存中实现瓦片索引唯一化，进行以下定义：

定义1主题金字塔是由相同类型的瓦片构成的瓦片集合，每一张瓦片可由主题、层级、列号与行号唯一确定。在实际应用中，由于瓦片请求URL 前缀往往包含瓦片的版本号、传感器信息、生成时间信息等，所以可以直接由URL的前缀生成主题信息。

基于主题金字塔的瓦片索引值tileId可表示为

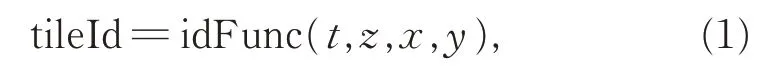
式（1）中，t表示瓦片主题，z表示瓦片在该主题金字塔中的层级号，x表示瓦片在z层级上的列号，y表示瓦片在z层级上的行号，idFunc为索引值生成函数，tileId可唯一确定服务器端的一张瓦片。

idFunc为降维函数，即将主题、层级、行号、列号所构成的四维数据降维成一维数据，以方便采用B树、Hash表等方式创建索引。为减小编码，加快编码计算速度，本文采用如图1所示的tileId 编码结构。

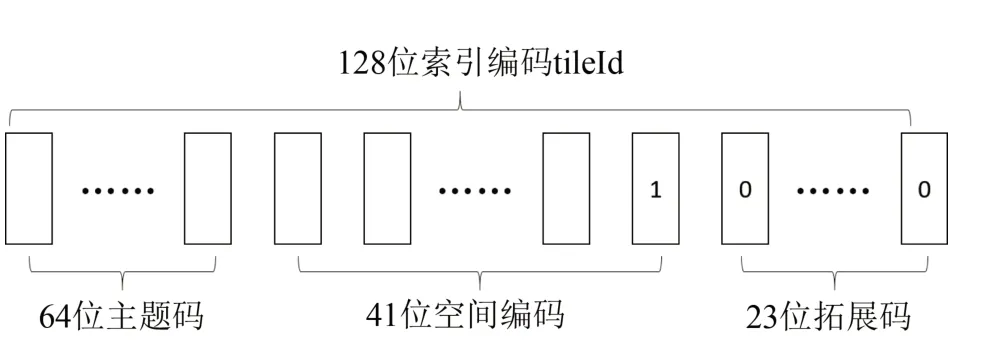
图1 索引编码结构Fig.1 Index coding structure

图1中，tileId占有128个二进制位，前64位表示瓦片的主题信息；中间41位为瓦片空间位置信息，最后一位为1，用来快速转换空间位置信息，即从末尾最后一位向前查找，找到第一个不为0的位置，设这一位的前一位置为pos（pos为64时表示0级瓦片），用第65位到位表示列号x，用位到pos位表示行号y,用表示层级号l，而依照地理信息公共服务平台电子地图数据规范，瓦片数据通常有1～20级，因此40位足以表示目前WebGIS常用瓦片范围；最后23位为保留位，可用于拓展瓦片层级。

在实际应用中，笔者根据瓦片请求URL 生成请求前缀preUrl、层级号l、列号x、行号y，采用MurmurHash 函数由preUrl 生成t值。同时，采用2级索引机制，即首先根据主题值t，检索到该主题下的瓦片索引表，再根据由主题值t、层级号l、列号x和行号y生成的索引tileId 在瓦片索引表中检索瓦片数据，为加快数据定位速度，索引项tileId 采用hash表存储。

基于主题金字塔的瓦片索引的结构如图2所示，第1级主题索引表themeIndex 实现主题值t与主题索引节点themeIndexNode的映射，themeIndexNode内容包括：请求前缀preUrl、缓存中该主题瓦片数目themeCount和第2级瓦片索引表tileIndex；第2级瓦片索引表tileIndex 实现瓦片索引值tileId与瓦片索引节点tileIndexNode的映射，tileIndexNode内容包括：上一次访问时间lastAccessTime、瓦片历史平均访问间隔avgAccessTime、基于邻接范围的空间访问频次freqSpatial、数据大小size、缓存数据价值gdtst和瓦片数据指针data。

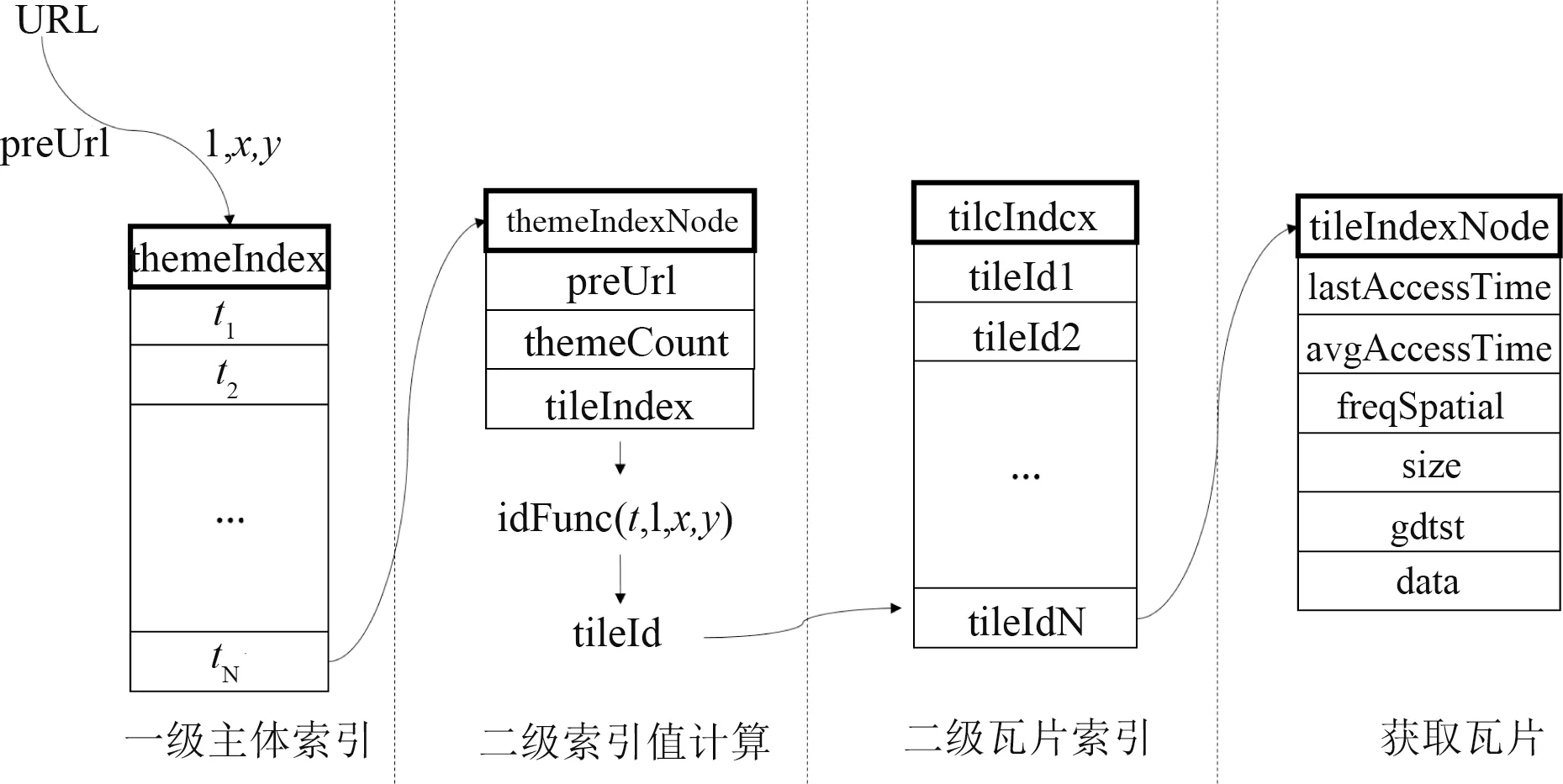
图2 2级瓦片索引结构Fig.2 Two-level tile index structure

2 基于主题时空价值的瓦片缓存置换算法

瓦片缓存服务器的空间大小是有限的，当缓存空间已满或达到某一阈值而无法容纳新的瓦片数据时，为了使缓存系统继续工作，就需要使用缓存置换算法将缓存中已有的瓦片替换出去。传统的缓存置换算法主要有：最近最少使用瓦片置换算法（LRU）、最不经常使用置换算法（LFU）、先进先出置换算法（FIFO）等，但这些算法忽视了瓦片数据的空间位置特性，不具备良好的瓦片命中率[9]；面向瓦片的缓存算法主要有TCLERPR、GDLVF、Stat、GUH 等[1,4-6]，这些算法均定义了自己的瓦片缓存价值，每次置换出价值最小的瓦片，较传统缓存算法效果好，但在面对服务器端的多套瓦片数据时无法进行很好的区分，并且对瓦片空间局部性利用欠充分。为此，提出了一种基于主题时空价值的瓦片缓存置换算法（GDTST算法），当缓存空间已满或达到阈值时，剔除gdtst值最小的瓦片，实现瓦片置换，gdtst值计算式为

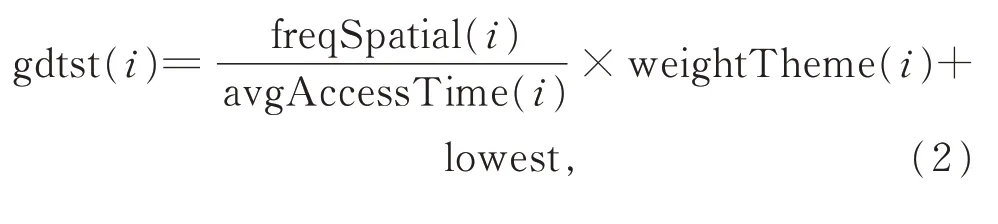
式(2)中，lowest表示当前缓存中瓦片价值的最低值，freqSpatial(i)表示当前瓦片基于邻接范围的空间访问频次，avgAcessTime(i)表示当前瓦片的历史平均访问间隔，weightTheme(i)表示瓦片主题权重。对于刚进入缓存的瓦片，gdtst值置为lowest。

2.1 基于邻接范围的空间访问频次

瓦片的空间局部性指在空间上距离相邻的瓦片总是倾向于在被访问的时间上也相邻，即地形漫游时，瓦片在某时刻被访问，则下一时刻该瓦片附近的瓦片有更高的概率再次被访问[8]。TCLERPR 等算法认为，瓦片访问的空间局部性体现在瓦片的长期流行度上，即用瓦片的累计访问次数来反映瓦片访问请求的空间分布特性。这种方式体现了瓦片访问空间局部性的长期趋势，可以很好地表现某一时间段内哪些区域的瓦片最有可能被访问，但是对于瓦片访问的短期局部性，即当某一瓦片被访问后，其邻近瓦片将在下一时刻被访问的概率升高这一特性没有很好体现。因此，本文提出基于邻接范围的空间访问频次，并做以下定义：

定义2瓦片邻接范围是指当某一瓦片被请求后，在主题金字塔的当前缩放层级上，该瓦片可以影响以当前请求瓦片为中心的正方形范围内瓦片被访问的概率，这一范围称为瓦片邻接范围。

设瓦片邻接范围大小为adjacent，则adjacent表示以当前请求瓦片为中心，邻接范围内瓦片数据集中的瓦片个数，adjacent可取1，9，25，…，(2n+1)2。如图3所示，当adjacent 取9时，瓦片（x，y）被请求后，阴影部分则为其邻接范围。

图3 瓦片邻接范围Fig.3 Adjacency range of a tile

定义3瓦片邻接影响度为某一瓦片被请求后，对其邻接范围内其他瓦片的影响程度。设瓦片邻接影响度为aw，aw的取值范围为[0,1]，值越大，瓦片的访问对其空间邻近瓦片的影响越大，aw=0,即不会影响对邻近瓦片的访问。

定义4基于邻接范围的空间访问频次。设freqSpatial为瓦片基于邻接范围的空间访问频次，当该瓦片被命中时，其freqSpatial=freqSpatial+1，缓存中该瓦片邻接范围内其余瓦片的freqSpatial=freqSpatial+aw；未被命中时，将该瓦片邻接范围内所有瓦片写入缓存，该瓦片的freqSpatial值为1，邻接范围内其余瓦片的freqSpatial值为aw。

freqSpatial 实质是瓦片的累计访问频次和其邻接范围影响权重的累加，反映了瓦片访问的长期局部性；而每一次瓦片freqSpatial的更新则是瓦片访问短期局部性的体现，反映下一时刻邻接范围内的瓦片被访问的概率将升高。为减少缓存对瓦片服务器的请求次数，本文在瓦片服务器上实现瓦片批量获取接口，即通过单次请求，获取瓦片邻接范围内所有瓦片；同时，当瓦片被命中时，仅更新缓存中邻接范围内已有瓦片的访问频次，不请求缺失的邻接范围瓦片。

2.2 瓦片历史平均访问间隔

瓦片的时间局部性是指如果某个瓦片对象刚刚被客户端请求过，那么在今后的一段时间内，该瓦片对象被再次访问的概率较高，并且随着访问时间间隔的缩短，被再次访问的概率会随之增大[10]。本文采用瓦片历史平均访问间隔来体现瓦片访问的时间局部性，即采用递进的方式来计算瓦片的平均访问间隔，从而实现既考虑瓦片的当前访问时间间隔，又兼顾历史访问时间间隔[11]。

定义5瓦片历史平均访问间隔。设avgAccessTime表示瓦片的历史平均访问时间间隔，lastAccessTime为瓦片上次被访问的时间，hw为历史瓦片访问权重，currentTime表示当前时间，当瓦片被再次访问时，avgAccessTime 按下式更新：

式(3)中，瓦片刚进入缓存时设置avgAcessTime为0，hw的取值范围为[0,1)，hw值越大瓦片的历史访问时间间隔对下一次访问影响越大，hw 取0时，则退化为LRU算法中的时间间隔，仅反映短期内该瓦片被访问的概率。

2.3 瓦片主题权重

服务器端瓦片对象除了具有时空局部性外，由于其具有不同的主题，用户访问时往往还有主题倾向性，即对相同价值的瓦片，用户倾向主题的瓦片数据被再次访问的概率要大于非倾向主题的瓦片数据，前者的实际数据价值大于后者[12]；同时，对于不同主题的瓦片金字塔，其瓦片大小差异较大。在计算面向服务器端的瓦片缓存价值时，还需考虑主题与数据大小相关因素，因此，本文定义了服务器端的瓦片主题权重。

定义6瓦片主题权重。设weightTheme为瓦片主题权重，themeCount为该主题金字塔缓存中的瓦片数目，totalThemeCount为缓存中的所有瓦片数目，size为瓦片大小，则

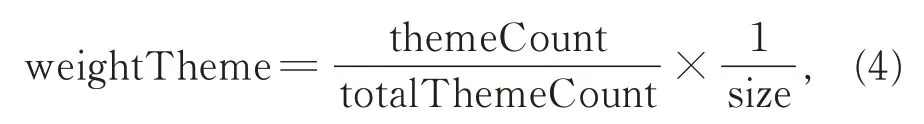
weightTheme 实质上通过缓存中不同瓦片主题所占比例来反映用户的主题倾向性，即认为缓存中某一主题瓦片数据所占比例较大，则下一时刻该主题的瓦片较其他主题的瓦片被访问的概率要大。同时为了提高瓦片对象的命中率，该权重与数据大小成反比，认为数据较小的瓦片权重更大，即应优先置换单个数据较大的瓦片而不是多个数据较小的瓦片。

2.4 基于主题时空价值缓存算法的流程

结合基于主题金字塔的瓦片缓存索引，GDTST算法的具体过程描述如下：

(1)当有新的请求到达缓存时，根据请求的URL信息生成瓦片的主题信息t、层级号l、列号x、行号y；

(2)根据t查找主题索引表themeIndex，如果未命中转(3)，命中转(4)；

(3)创建并初始化主题索引节点themeNode，加入一级索引表themeIndex，转(6)；

(4)获取主题索引节点themeNode，根据瓦片t、l、x、y生成瓦片索引tileId，根据tileId查找themeNode的瓦片索引表tileIndex，如果命中转(5)，未命中转(6)；

(5)获取该瓦片索引节点，返回被请求瓦片数据，更新该节点的lastAccessTime、avgAccessTime、freqSpatial和gdtst；更新该瓦片邻接范围内其余瓦片索引节点的freqSpatial和gdtst，若邻接瓦片不在缓存中，则跳过，转(10)；

(6)根据t、l、x、y构造瓦片及其邻接范围内其余瓦片的URL，从源瓦片服务器获取瓦片邻接范围内所有瓦片，同时，返回被请求瓦片；

(7)判断缓存空间是否足以容纳邻接范围内所有瓦片，若不足转(8)，若足够转(9)；

(8)移除缓存中主题时空价值最低的瓦片，并移除相应索引项，直到缓存空间充足；

(9)对于每一张瓦片，生成其tileId，当tileId 在索引中时，仅更新其瓦片索引节点的freqSpatial和gdtst；当tileId 不在索引中时，创建并初始化瓦片索引节点，加入到二级索引表tileIndex中，并将瓦片数据加入缓存。

(10)结束。

在实际应用中，步骤(5)和(6)中的返回瓦片数据操作和其余缓存更新操作异步进行，因此邻接范围内瓦片的更新不会影响瓦片数据的返回延时。同时，对于步骤(6)请求的邻接范围瓦片操作，当瓦片服务器实现批量获取接口时，仅需请求1次便可获取邻接范围内瓦片，对源瓦片服务器不会产生额外的负载。

3 实验与分析

3.1 实验内容与环境

采用日志驱动模式，考察GDTST算法对多主题瓦片数据的请求命中率、字节命中率和延迟节省率三方面的性能。首先，采集在不设置缓存情况下的源瓦片服务器日志记录；接着，按请求时间顺序提取日志中瓦片请求的URL 信息，生成测试文件；然后，测试客户端程序，按照测试文件模拟用户访问，向缓存服务程序请求瓦片；最后，在不同相对缓存大小下，计算采用LRU、LFU、FIFO与GDTST 缓存算法时缓存服务程序的3项指标值。其中，相对缓存为实际缓存空间相对所设定最大缓存容量（2GB）的百分比。

实验采集的日志记录为近海碳通量信息可视化系统[13]瓦片服务器2018年10月23日的被访问记录，共141 236 条日志，涉及241种瓦片产品数据。其中，最大的瓦片为134.7 kB，最小的瓦片为668 B。硬件环境为2台相同的小型服务器，其中一台服务器部署测试客户端程序，另一台服务器部署缓存服务程序和瓦片服务程序，2台服务器通过千兆交换机相连。服务器配置：Windows 7，64位操作系统，Intel(R)Core(TM)i7-4790 CPU @3.60 GHz，8 核CPU，8 GB内存。

3.2 GDTST算法的参数选择

在GDTST算法中，需要设置历史瓦片访问权重hw、瓦片邻接影响度aw和瓦片邻接范围adjacent。其中，瓦片邻接范围的选取主要依据缓存空间的大小，在最大缓存容量2 GB的条件下，本文设置adjacent=9，并进一步进行hw和aw的选取。

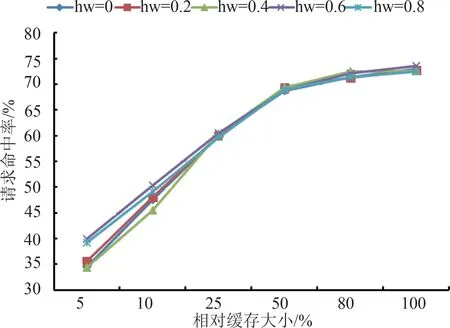
图4 hw 参数选取比较Fig.4 The comparison of hw parameter selection

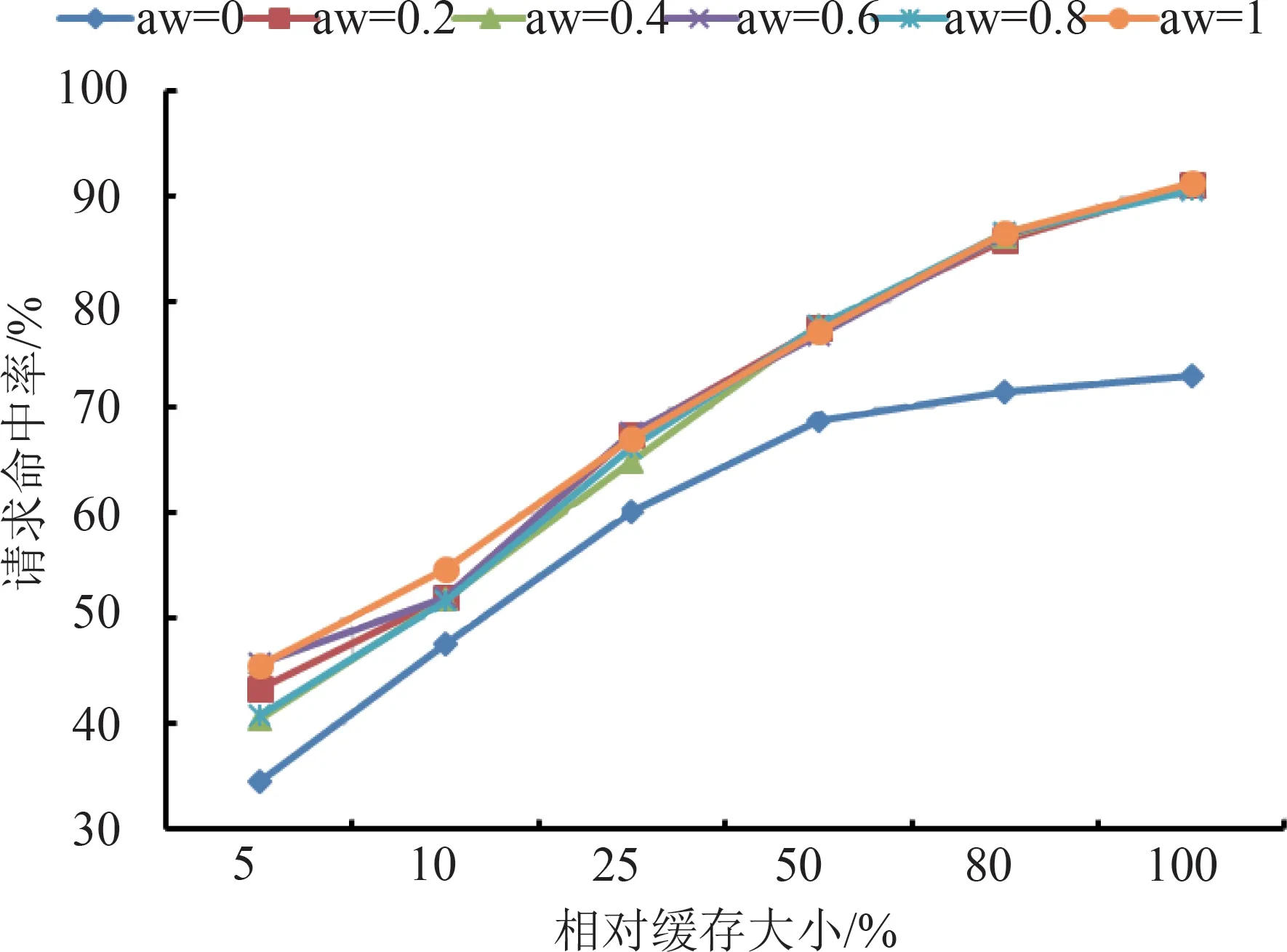
图5 aw 参数选取比较Fig.5 The comparison of aw parameter selection

图4为瓦片邻接影响度aw 设置为0时，采用不同历史瓦片访问权重hw的GDTST算法请求命中率结果。由图4可知，当相对缓存大于25%时，GDTST算法对于瓦片历史访问权重参数不敏感；而当相对缓存小于25%时，可以发现当历史瓦片访问权重取0.6 或0.8时，较取其他值时获得了更高的瓦片请求命中率。

图5为历史瓦片访问权重hw 设置为0时，采用不同瓦片邻接影响度aw的GDTST算法请求命中率结果。由图5可知，瓦片邻接影响度参数大于0时的请求命中率明显大于瓦片邻接影响度等于0时。同时，当相对缓存大于50%时，请求命中率对于瓦片邻接影响度大于0的不敏感；而当相对缓存小于50%时，瓦片邻接影响度参数取1时，可以获得更高的请求命中率。

为了获得更高的缓存命中率，在缓存算法对比实验中，GDTST算法的参数分别取hw=0.6，aw=1，adjacent=9。

3.3 实验结果与分析

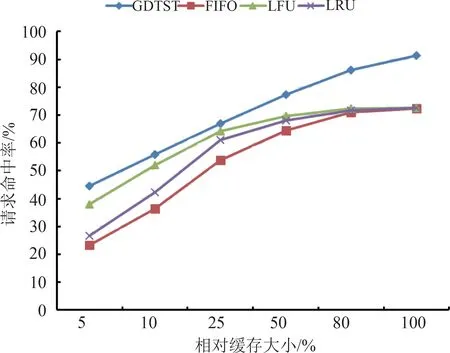
图6 请求命中率比较Fig.6 The comparison of the request hit ratio

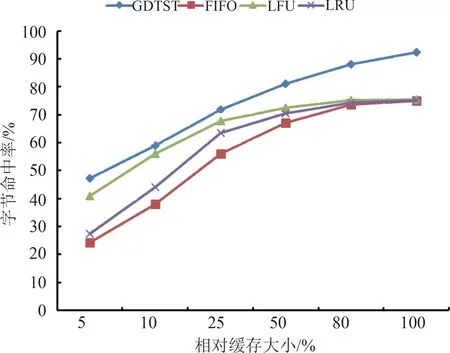
图7 字节命中率比较Fig.7 The comparison of the byte hit ratio

图6和图7分别为FIFO、LFU、LRU和GDTST4种缓存算法的请求命中率和字节命中率的实验结果。由实验结果可知，4种缓存算法中，2种缓存命中率会随缓存的增大而增大；当相对缓存较小时，4种缓存算法命中率均随缓存容量的增加明显变化；当相对缓存容量较大时，4种缓存算法随缓存容量增加变化较为平缓，FIFO、LFU、LRU 瓦片请求命中率最终趋近于重复请求在所有请求中所占的比例，而GDTST算法，由于每次未命中会提前缓存邻近范围瓦片，故其命中率的趋近值更大。而在相对缓存大小相同的情况下，GDTST算法的命中率均高于其他3种算法，这是由于GDTST算法综合考虑了瓦片访问的时空局部性，特别是短期空间局部性，同时也利用了用户对于瓦片访问的主题倾向性，因而在多主题瓦片的访问情景下可以获得更好的命中效果。

由于仅在被请求瓦片缺失时才会访问源瓦片服务器，且本文在瓦片服务器端实现了瓦片批量获取接口，当邻接范围瓦片更新时，GDTST算法不会导致额外的瓦片请求，因此，其瓦片请求命中率与源瓦片服务器的接收请求率相关，即瓦片请求命中率越高，源瓦片服务器接收请求率越低。

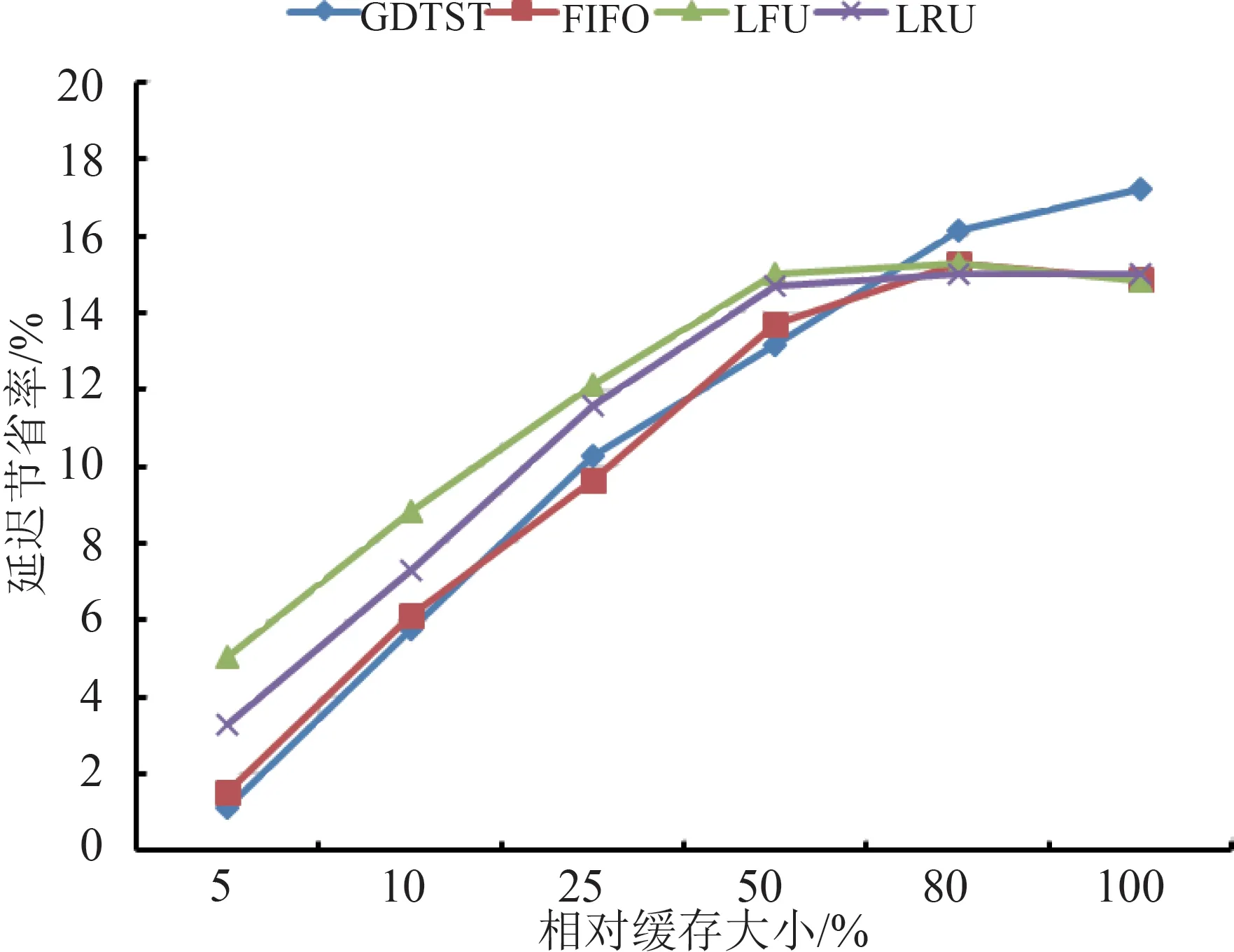
图8 延迟节省率比较Fig.8 The comparison of latency reduction ratio

图8为FIFO、LFU、LRU和GDTST4种缓存算法延迟节省率的实验结果，由实验结果可知，在相对缓存容量小于80%时，GDTST算法的延迟节省率与FIFO 相当，但小于LRU和LFU，这是由于GDTST算法的实现基于优先队列，其写入与调整操作都是O(log(n))的时间复杂度，而LRU、LFU和FIFO的写入与调整则实现了O(1)的时间复杂度，同时，在相对缓存较小时，缓存置换操作又较为频繁，因此，当相对缓存容量较小时，其延迟节省率略低于LRU和LFU，当缓存容量在10%～80%时，差值小于3%；而当缓存容量大于80%时，GDTST算法由于其较高的缓存命中率，瓦片命中节省的时间弥补了算法的复杂度，因此，其延迟节省率高于其他3种算法。

4 结 论

设计了面向多主题瓦片数据的服务器端缓存索引，综合考虑瓦片请求的时间局部性、空间局部性和用户主题倾向性，提出了GDTST算法。实验结果表明，相较于传统FIFO、LRU、LFU算法，当面对源瓦片服务器中多主题瓦片数据时，在不同的相对缓存下，GDTST 均能取得较高的瓦片请求命中率和字节命中率，同时，在相对缓存较大的情况下拥有更高的延迟节省率，因此，GDTST算法可以有效减轻源瓦片服务器负载、缩短用户等待时间。但是，GDTST算法缓存更新操作时间复杂度较高，下一步工作将优化缓存数据结构，在相对缓存较小时提高缓存算法延迟节省率。