广义拟Sugeno积分的次可加性和自连续性
2020-03-12李艳红
李艳红
(辽东学院师范学院数学系,辽宁丹东118003)
0 引言
自1974年日本学者SUGENO[1]首次引入模糊测度概念以来,模糊积分理论得到不断丰富和发展,但由于模糊测度不具有一般可加性,因而无法建立类似于经典测度论的理论体系。为克服这一缺陷,许多学者在模糊测度限定条件下做了大量探究。1984年,WANG[2]首次提出集函数的自连续、伪自连续、零可加和伪零可加等概念,并依此讨论了可测函数列和积分序列的收敛性。1987年,SUGENO 等[3]再次通过公理化方法引入拟加法和拟乘法,并初步建立了拟可加积分模型及其理论框架。1993年,蒋兴 忠[4]基 于 文 献[3],引入 了2种算子(K和t算子),建立了tK积分和Kt积分,并讨论了这两类积分的基本性质和收敛定理。1998年,王贵君等[5]将K算子和t算子统一化,提出诱导算子概念,并建立了K-拟可加积分,进而讨论这种积分的绝对连续性和自连续性[6]。2010年,李艳红等[7]在K-拟加模糊测度空间上对广义实函数建立了广义Sugeno模糊积分,继而通过诱导算子研究了广义拟Sugeno模糊积分的3种确界式等价表示,并通过实例计算验证了该积分的等价性[8]。这些结果不仅丰富了模糊积分的研究领域,而且也为模糊积分的应用提供了理论基础。
此外,虽然已有文献研究一些模糊积分的次可加性[9-10],但其绝大多数都是针对被积函数的,即使考虑积分区域,也是以限定两可测集不相交为前提。基于文献[7-8],本文将广义拟Sugeno积分整体看成取值于非负实数的集函数,突破以往两可测集交为空集的约束条件,给出该集函数的次可加性,进而利用次可加性讨论广义拟Sugeno积分的自连续性和零可加性。
1 预备知识
设X是一个经典集合,R+=[0,+∞],ℜ是X上若干子集构成的σ-代数,(X,ℜ)代表给定的任一可测空间,N表示自然数集。
定义1[4-5]设K:R+→R+是严格增加的连续函数,且满足条件:(i)K(0)=0,K(1)=1,(ii)则称K为R+上诱导算子,并约定(+∞)⋅0=0 ⋅(+∞)=0。
显然,K的逆算子K-1仍递增,且K-1也是诱导算子。详见文献[4-5]。
定义2[4-5]设K是给定诱导算子,∀a,b∈R+,界定a与b的K-拟加运算⊕与K-拟乘运算⊗为:
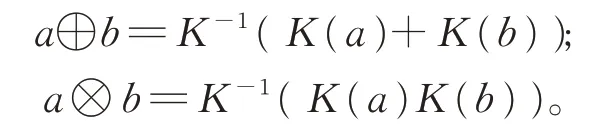
故∀a,b,c,d∈R+,不难得到以下结论:
(i)a⊕b=b⊕a,a⊗b=b⊗a,a⊗(b⊕c)=(a⊗b)⊕(a⊗c);
(ii)a⊕0=a,a⊗0=0,a⊗1=a;
(iii)若a≤b,c≤d,则有a⊕c≤b⊕d,a⊗c≤b⊗d;
(vi)K(a⊕b)=K(a)+K(b),K(a⊗b)=K(a)⋅K(b);
(v)K-1(a+b)=K-1(a)⊕K-1(b);K-1(a⋅b)=K-1(a)⊗K-1(b);
定义3[3]设(X,ℜ)是可测空间,K是诱导算子,若集函数̂:ℜ →[0,+∞]满足:
(i)̂(∅)=0;
(ii)若A,B∈ℜ,且
则称集函数̂为K-拟加测度,相应地称三元组(X,ℜ,̂)为K-拟加测度空间。
定义4[8]设(X,ℜ,̂)是K-拟加测度空间,K是诱导算子,f:X→[0,+∞]是非负可测函数,A∈ℜ,令
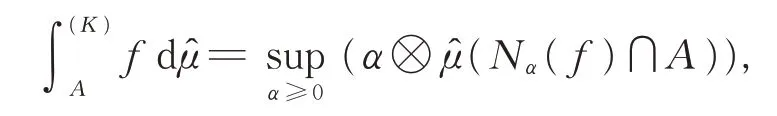
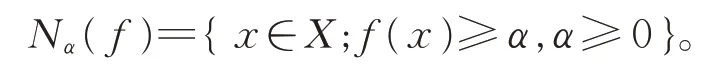
注1实际上,拟加⊕和拟乘⊗算子均借助诱导算子K给出,特别地,当K(x)=x时,显然有a⊕b=a+b;a⊗b=a⋅b。故⊕和⊗算子分别是普通加法和乘法的推广。此外,从基于值域 [0,+∞]来看,K-拟加测度μ̂已不再具有模糊性,故所定义的积分也不必称之为模糊积分。另一方面,依据文献[4-5],显然可得supK-1(⋅)=K-1sup(⋅),再由定义2,立刻可得广义拟Sugeno积分的另外2种等价表示:
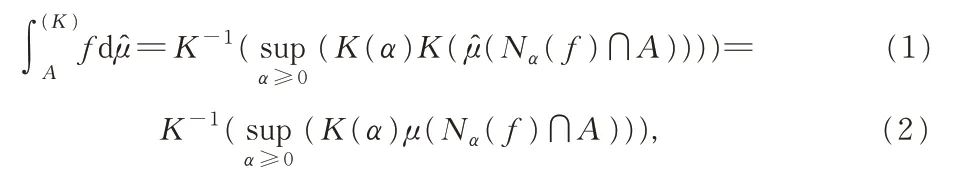
其中μ(⋅)=K(μ̂(⋅))恰是Lebesgue 测度。
下面,通过一个实例来计算这种广义拟Sugeno积分的值,以便从中发现该积分的值是随诱导算子的变化而变化的。
例1 给定一个非负可测函数f(x)=2x+3,x∈R+,取A=[1,3],̂为K-拟加测度。取诱导算子:(i)K(x)=x2,(ii)K(x)=x3,分别计算积分值
解首先,依据截集定义,∀α≥0,必有
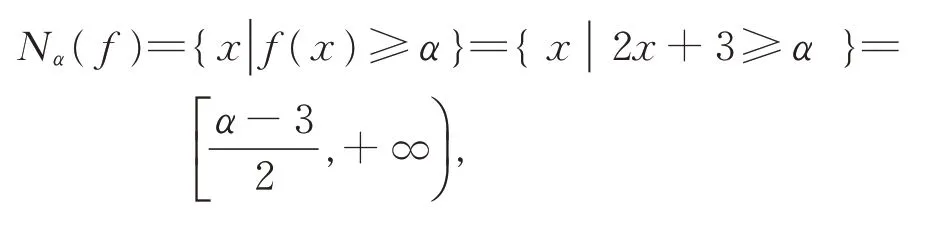
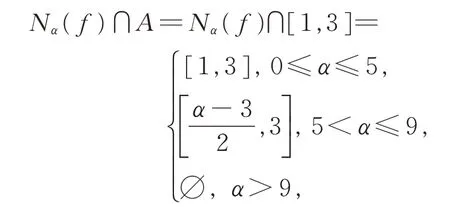
因此,依据Lebesgue 测度可得
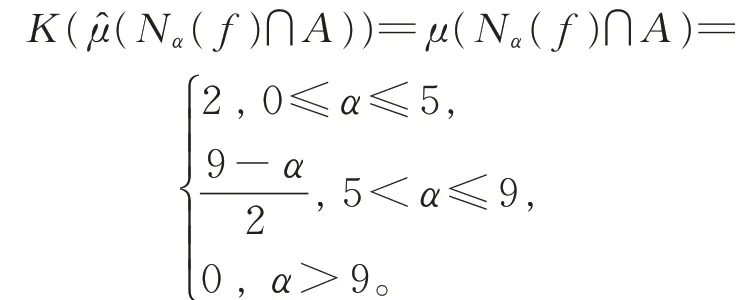
情况(i)K(x)=x2,由广义拟Sugeno积分的等价表示式(2),容易获得
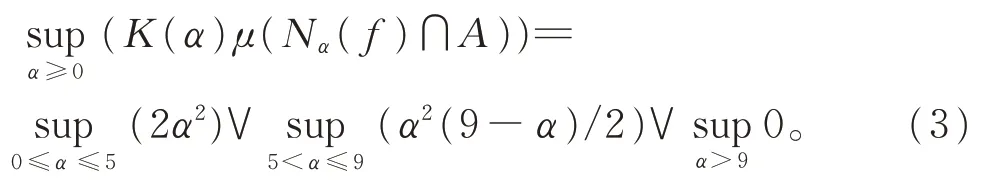
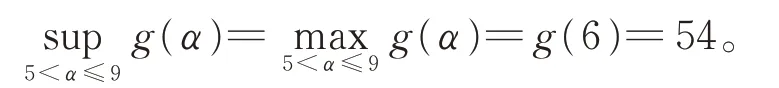
则式(3)为
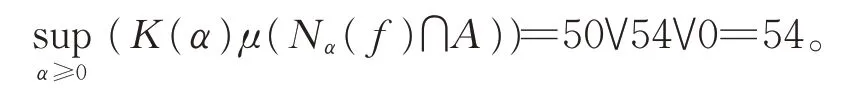
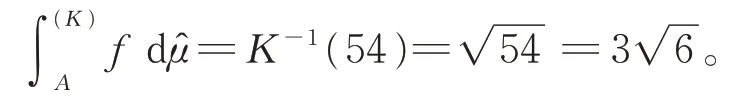
情况(ii)K(x)=x3,由式(2)可得
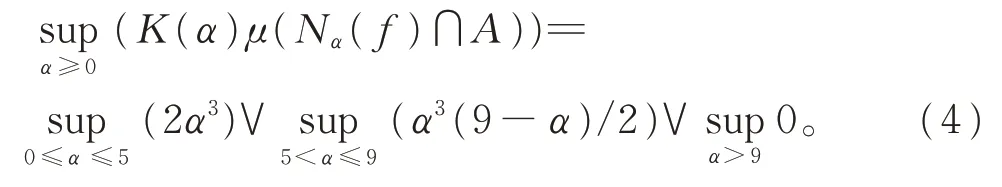
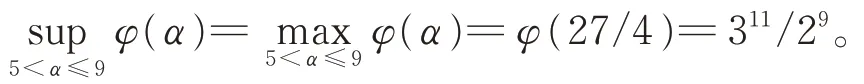
因K-1(x)=x3,再由式(2)~(4),立刻可得
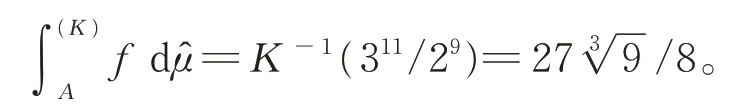
显然,在其他条件不变的情况下,不同诱导算子所对应的广义拟Sugeno积分的值不同。
下面,为了继续讨论广义拟Sugeno积分的自连续性和零可加性,给出可测空间上集函数的零可加(减)和上(下)自连续的定义。
定义5[2]设(X,ℜ)是任一可测空间,集函数μ:ℜ →[0,+∞]。∀A,B∈ℜ,若满足μ(B)=0 ⇒μ(A∪B)=μ(A)(或μ(A-B)=μ(A)),则称μ是零可加(或零可减)的。
定义6[2]设(X,ℜ)是任一可测空间,集函数μ:ℜ →[0,+∞]。若∀{An}⊂ℜ,A∈ℜ,满足
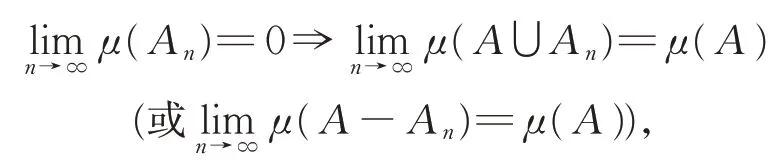
则称μ是上自连续(或下自连续)的。若μ既是上自连续的,又是下自连续的,则称μ是自连续的。
2 次可加性
若将广义拟Sugeno积分的等价表达式(1)或(2)整体看成可测空间上的集函数,则可进一步讨论这种集函数的基本性质,如次可加性。故为证明广义拟Sugeno积分(看成集函数)对任意2个可测集关于拟加法⊕满足次可加性,首先给出一个引理。
引理1设(X,ℜ,μ̂)是K- 拟加测度空间,∀A,B∈ℜ,且A⊂B,则̂(A)≤μ̂(B)。
证明因当A⊂B时,有B=A∪(B-A),且由定义3 必有故K-拟可加测度̂是单调递增的。
推论1在定义4 条件下,若令v(A)=,则集函数v也是单调递增的。
引理2设(X,ℜ,̂)是一个K-拟加测度空间,μ(⋅)=K(̂(⋅)),A∈ℜ,则广义拟Sugeno积分内部表达式在α≥0和α>0时的上确界相等,即
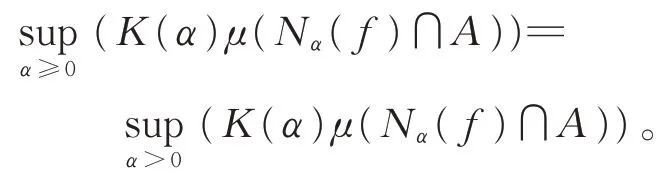
证明由定义1,诱导算子K满足K(0)=0,则有
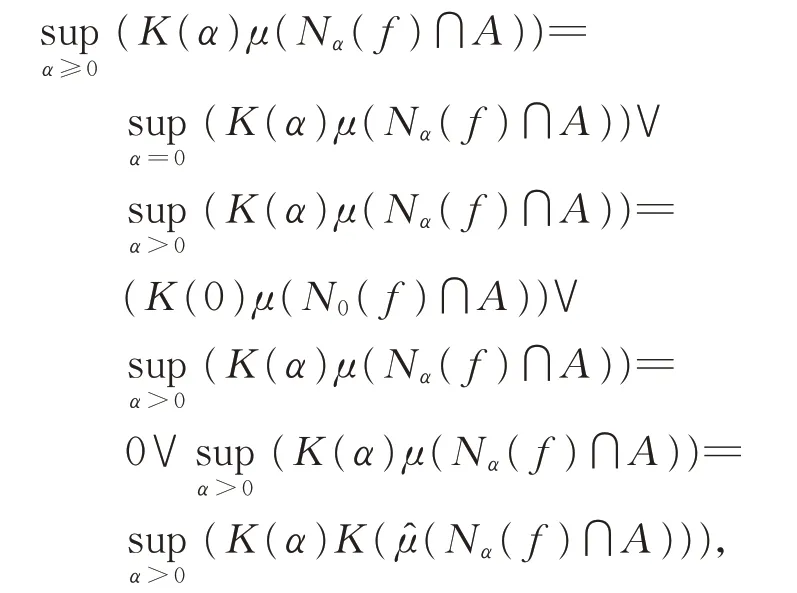
当α=0时,即使μ(N0(f)∩A)=+∞,依定义1 约定也总有K(0)μ(N0(f)∩A)=0。
下面,在废除2个可测集交为空的限定条件下给出重要结论:广义拟Sugeno积分(看成集函数)对任意2个可测集关于拟加法⊕满足次可加性。
定理1设(X,ℜ,μ̂)是给定的K-拟加测度空间,∀A∈ℜ,若令,则∀B∈ℜ,集函数v必满足v(A∪B)≤v(A)⊕v(B)。
证 明因A∪B=A∪(B-A),且A∩(BA)=∅。由式(2)和Lebesgue 测度μ的可加性得
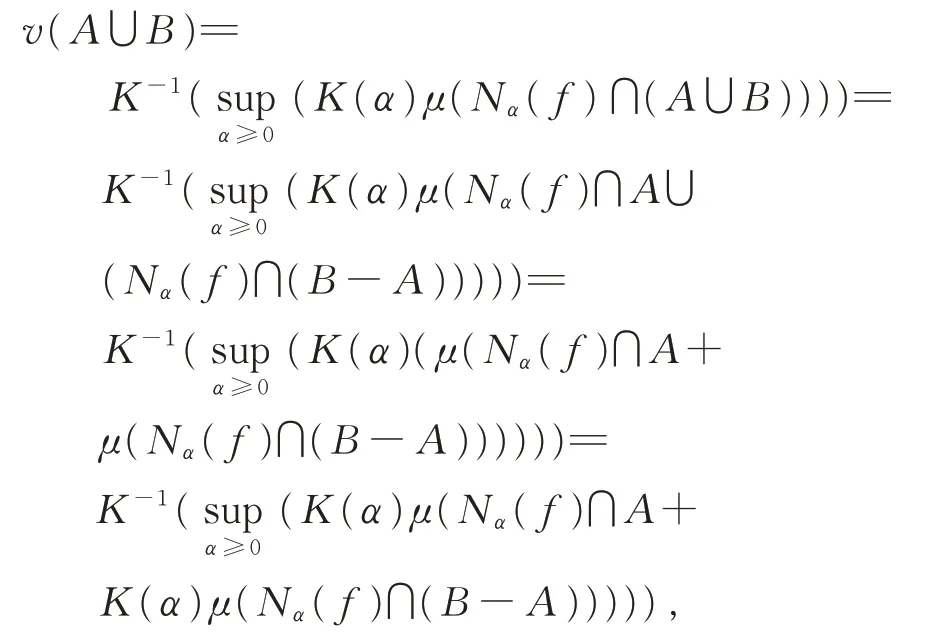
此时,由于对任意非负有界函数f(x),g(x),总有sup(f(x)+g(x))≤supf(x)+supg(x),且B-A⊂B,更有μ(Nα(f)∩(B-A))≤μ(Nα(f)∩B)。再由K-1的递增性可得

注2需要强调的是,虽然有些文献讨论了某模糊积分关于积分区域的次可加性,但大多是在A∩B=∅情况下进行的讨论。而定理1 正是在2个可测集为任意的条件下获得的广义拟Sugeno积分(看成集函数)的次可加性。当然,上述次可加性v(A∪B)≤v(A)+v(B)也可等价表示为
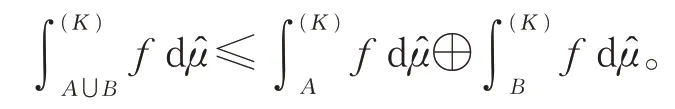
3 自连续性
类似第2节的方法,若仍将广义拟Sugeno积分的等价表示式(1)整体看成可测空间上的集函数,则由这种集函数的次可加性还可继续探究广义拟Sugeno积分(集函数)的零可加性和自连续性。
定理2设(X,ℜ,μ̂)是给定的K-拟加测度空间,∀A∈ℜ,若令则集函数v是零可加的,进而v也是零可减的。
证明由定义5,若要证v是零可加的,只需证:若v(B)=0,则有v(A∪B)=v(A)。
事实上,由引理2和式(1),若令
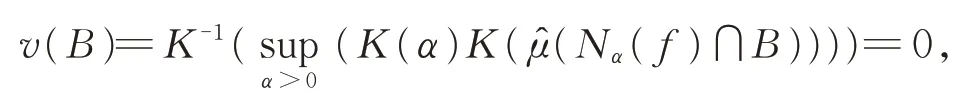
则对∀α>0,必有
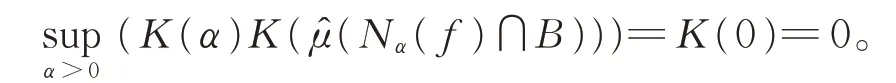
再由B-A⊂B,有
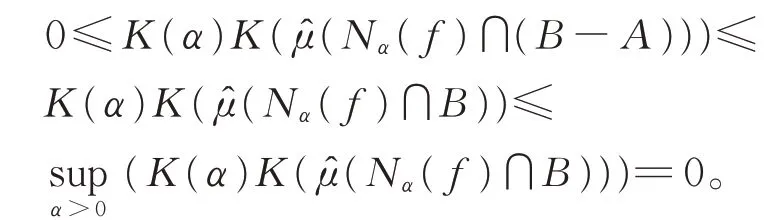
故K(α)K(μ̂(Nα(f)∩(B-A)))≡0。
因K(α)>0,则有
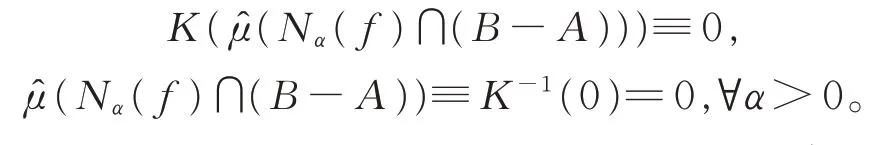
由A∪B=A∪(B-A),且A∩(B-A)=∅,∀α>0,及定义3可得

再由式(1)立即可得
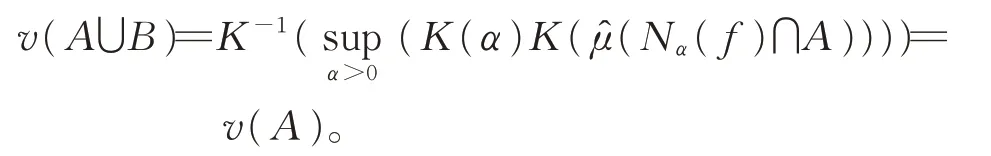
因此,集函数v是零可加的。
下证集函数v也是零可减的。
事实上,∀A,B∈ℜ,若设v(B)=0,则总有A=(A-B)∪(A∩B),且A∩B⊂B。由推论1,有0≤v(A∩B)≤v(B)=0。故v(A∩B)=0。再 由 定理2中v的零可加性,自然有
v(A)=v((A-B)∪(A∩B))=v(A-B)。因此,集函数v也是零可减的。
定理3设(X,ℜ,μ̂)是K- 拟加测度空间,∀A∈ℜ,若令,则v是自连续的。
证明首先,证明集函数v是上自连续的。不妨设A∈ℜ,集合列 {An}⊂ℜ,且满足往证
事实上,依定理1(v的次可加性)及v的单调性,显然有
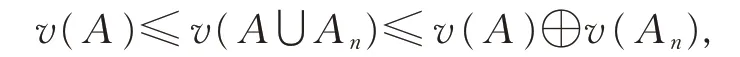
由定义2(vi),显然有
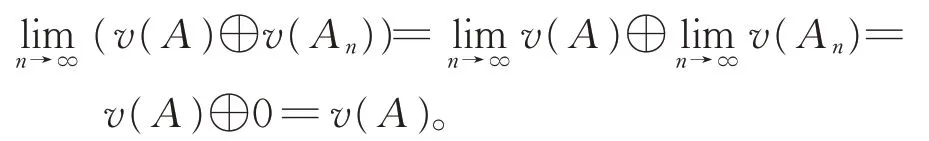
其次,证明v也是下自连续的。假设同前,只需往证实际上,∀n∈N,总有A⊂(A-An)∪An,再由定理1,必有
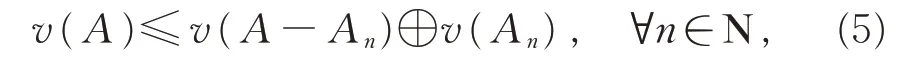
因暂无法确认数列{v(A-An)}的极限是否存在,故两端不宜直接取极限。但由可得,∀ε>0,∃N∈N,当n>N时,总有v(An)<ε。故有K(v(An)) 由定义2,将式(5)等价变换为普通加法,然后进行移项处理,即 再由A-An⊂A⇒v(A-An)≤v(A)⇒K(v(A-An))≤K(v(A))。 故有 令n→∞,由诱导算子K的连续性,易得 再基于式(6)和夹逼定理,知数列{K(v(A-An))}收敛,且满足 由K的严格单调性(或K-1作用两边),必有即集函数v也是下自连续的。因此,集函数v自连续,或者说广义拟Sugeno积分是自连续的。 注3在定理3中,若取An≡B,显然可由v的上自连续推得v零可加,由v的下自连续推得v零可减。因此,此事实与集函数上(下)自连续蕴含零可加(减)是一致的。 在废除2个可测集交为空的限定条件下重新给出了广义拟Sugeno积分(看成集函数)关于拟加法⊕满足次可加性,进而利用次可加性证明此广义拟Sugeno积分的零可加(减)性和上(下)自连续性,并给出自连续和零可加(减)的蕴含关系。所得结果丰富了传统非可加积分理论,为进一步研究广义拟Sugeno积分的特性提供了新的思路和方法。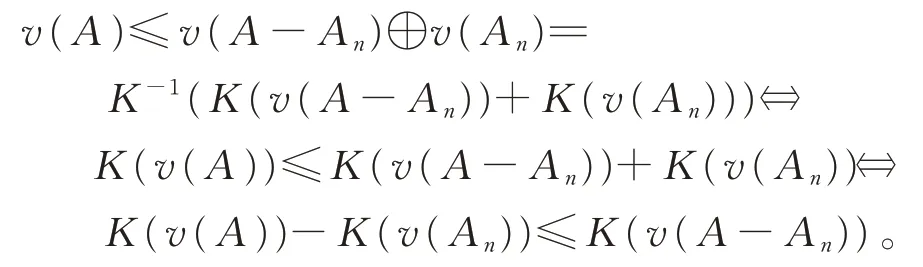
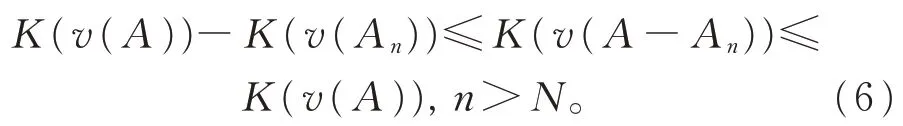
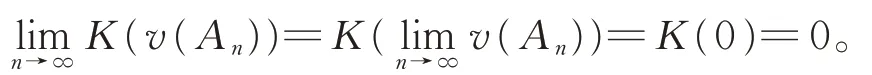
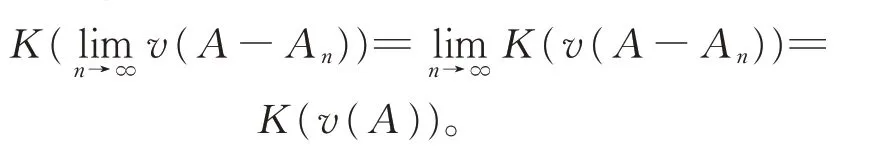
4 结 论
