论辟斯顿弦乐四重奏作品中音高结构的对称形态
2020-03-12张宝华
张宝华
“沃尔特·辟斯顿(Walter Piston,1894—1976)是20 世纪美国音乐史中最伟大的作曲家与音乐理论家之一,其一生共创作了七十余部作品,包括八部交响乐、十七部管弦乐、五部弦乐四重奏、六部协奏曲和近三十部室内乐。”①张宝华:《辟斯顿综合调式半音体系下的非三度结构和声语言——以五部〈弦乐四重奏〉为例》,《黄钟》2019年第1期,第122-123页。作为20世纪新古典主义作曲家的代表,国内学界针对辟斯顿作品的研究相对较少,其作品中饶有趣味的音高结构对称形态还没有引起人们足够的重视。本文拟针对辟斯顿弦乐四重奏作品中的横向与纵向音高结构对称形态进行分类、总结和论析。
提到对称,一定会使人联想到“镜像”。镜像是否等于对称?亦或是两者有所区别?因为本文研究横向旋律和纵向音高结构时会多次提及这两个术语,所以首先需要将“对称”和“镜像”加以区分和解释。音乐学家拉瑞·所罗门(Larry Joseph Solomon)在其博士论文《对称性作为作曲技术的决定性因素》(Symmetry as a Determinant of Musical Composition)②Larry Joseph Solomon:Symmetry as a Determinant of Musical Composition,West Virginia University,1973,p.23.中将对称结构分为重复(repetieion)、模进(sequence)、平移(translation)、旋转(ratation)和镜像(mirrored)五种类型。从这种分类状态看,“镜像”被包含在“对称”之中。
从理论角度加以概括,“对称”可大致分为以下三类:①镜像对称:倒影(反行)、逆行、倒影逆行;②平移对称:重复、模进(平行);③旋转对称:倒影-逆行(逆反行),也包括其它形式化的旋转关系。由此可见,“镜像”是三种对称形式中的一种。以下部分将对辟斯顿旋律中存在的“对称”现象进行概括与总结。
“镜像”一词在20 世纪之前的音乐理论中并不常见,它似乎显得过于“冰冷”,与音乐有些格格不入。但是它又好像被我们所熟知,因为作曲技法中的“倒影”一词就含有“水平界面的反射”之意。所以从某种程度上讲,倒影可以与“水平镜像”划等号,比如“倒影卡农”又可称之为“镜像卡农”。但是这个词更多是用在复调音乐中。另外,20 世纪作曲家作品中也经常会出现“镜像结构”③姚恒璐:《镜像与透视——音乐作品中结构比例的共性》,《交响》2001年第3期,第30页。特征,兴德米特和新维也纳乐派作曲家的作品似乎对这种曲式结构更加情有独钟。
镜像原则需要三个条件:①“物”的存在;②“镜”的存在;③“物”与“像”在“镜”前后的对称且同时存在。
从这三点中不难看出镜像原则的主要特征。首先,物是构成镜像的先决条件;其次,“镜”是成“像”的“折射”条件,也就是说“物”的存在如果想要得出其反射的“像”,必须有真实的“镜”作为反射点,没有“镜”,则其“像”也不成立;最后,本体和反射体在“镜”前后的同时存在,即“物”与“像”在“镜面点”前后的对应状态,即形成镜像。
一、线性声部中音高结构的对称形态
本文在分析单一旋律构成手法时,借鉴了三种镜像结构中的“垂直镜像”④三种“镜像结构”分别为:水平镜像——相当于作曲技法中的“倒影”;垂直镜像——相当于作曲技法中的“逆行”;斜向镜像旋律——相当于作曲技法中倒影、逆行技术的结合。这一术语来形容辟斯顿发展单一旋律声部的一种典型手段,这一部分的论述可以看作是辟斯顿“镜像”与“对称”原则的“初级”体现。
(一)垂直镜像对称
“镜像旋律”是指旋律或旋律片段中某个音可以作为轴音,两边的旋律音以轴音为中间点,形成一种对称的镜像关系。从“镜像”的篇幅来看,它可以是一个动机,也可以是一个乐句或乐段。⑤蒋奕菲:《镜像结构研究》,上海音乐学院2010年硕士学位论文,第8页。从更加宏观的曲式结构意义来看,“镜像结构”原则在20 世纪的音乐作品中屡见不鲜,贝尔格作品中的“回文结构”以及韦伯恩的“微观镜像曲式结构”,便是镜像原则的一种“宏观”意义。在辟斯顿早期作品中,往往在一条旋律中会存在多个镜像片段,它们的轴音(相同轴音可以移高或移低八度)可能相同,也可能不同。
谱1 是SQ-1-I⑥SQ-1-I为《第一弦乐四重奏》第I乐章的英文简写,为节省篇幅,文中对作品名称和乐章采用此简写形式。的副部主题b 句(第54—62小节),从中可以看到这个由六声音阶构成的旋律框架主要是由F 和两个音为中轴,轴音前后相对应的音程呈现出镜像对称特征,轴音的选择也往往是调式的“框架音”。

谱1 《String Quartet 1-I》第54—62小节,副部主题b句旋律
首先需要确定的是,这个六音构成的旋律是f 调,因为大提琴声部在中提琴旋律开始的位置演奏了F、C、这个三和弦。这是辟斯顿惯用的明确旋律开始调性的主要手段之一。正如勋伯格所说:“每一个孤立的和弦,就其本身来说,都可以表示某一个调,如果无对抗和弦,它可以被看作是主和弦。”⑦[奥]阿诺德·勋伯格:《勋伯格:风格与创意》,茅于润译,上海:上海音乐出版社2011年版,第172页。辟斯顿就是在谱1 这个片段的开始处,用一个孤立的F 小三和弦来表明这个区域的主音是F。
其次,谱1 旋律曲线中存在着大量片段化的“镜像”结构,这是辟斯顿早期和中期作品中常见的现象。这种旋律构成方式既可以突出高点音和低点音在旋律中的“骨架”作用,也可以随时控制旋律起伏及其走向。
再次,这种“镜像”结构不仅仅体现在横向旋律线条,在二声部、三声部的对位化写作以及纵向和弦或和音的构成形式中,也存在着这种“镜像”结构。如果将横向旋律的“镜像”音高加以纵向排列,便会形成对称和弦。
最后,我们会联想到镜像原则的关键——“轴音(Pivotal note)”或“轴音程(Pivotal inter‐val)”,这一点在后文中会多次从不同角度论述。因为除了其中第一个轴音 与两边的G形成镜像旋律外,随后的F 音同样起到了“镜像轴心”的作用。
通过对谱1 中SQ-1-I 副部主题调式加以总结,可以清晰地看到人工“六声音阶”(见谱2),它们的半音数比例为——2:1:3:3:2:1为六声音阶的轴音。旋律下方的F、C小三和弦是Vc.声部与Vla.旋律声部于开头处齐奏出的。它可以被视作整个段落的主和弦,谱2 中总结的音阶也是将F 音作为主音。但是该人工音阶中并没有C 音。所以此处有着大、小调和弦与人工音阶旋律相结合的处理方式。

谱2 《String Quartet 1-I》第54—62小节副部主题b句音阶
(二)水平镜像对称
水平镜像在传统复调音乐中经常出现,它最典型的方式是倒影卡农。相区别的是,水平镜像的两个声部旋律在20 世纪的作品中既能够以传统卡农方式出现,同时也可以在相同节拍节奏模式下同时呈现。此处不过多论述传统倒影卡农形式,重点举出辟斯顿弦乐四重奏中相同节奏的二声部和四声部的水平镜像谱例。在辟斯顿的中晚期作品中,两个声部或四个声部同时出现的水平镜像旋律较为常见。
就像某些音阶在严格倒影状态下会产生另一个对称声部一样,在同样的主题-动机化发展方式下,两个声部在严格倒影的主题-动机模进下也同样可以产生两个旋律中的水平镜像。谱3中,可以简单划分出三个材料,尽管这三个材料都可以从第51小节的Vl.I声部中找到根源,但此处的主要目的并不是为了划分材料,而是为了更直观地将这个片段各声部的发展手法,以及产生两个外声部镜像旋律的根源表述清楚。

谱3 《String Quartet 2-I》第51—54小节
材料I指前两小节Vl.I声部相同材料的模进,Vl.II 声部还出现了五声音阶,材料I 位置可以看到两个外声部有着倒影形态,但从谱4 中的半音数分析可以看出,由于局部音高并不是严格倒影,所以还不能算作真正意义的水平镜像旋律。

谱4 《String Quartet 2-I》第51—54小节,外声部的水平镜像图示
材料III是相对静止的区域,其中Vl.I声部的“人工主音”D 和Vc.声部的“人工主音”C 被强化。这两个音与之前的“镜像2:1人工音阶”的轴音形成了上下半音关系的“对称主音”。其中C 和D 是横向声部的主音,而具有纵向音高结构“镜像轴”的主音特征,综合这三个“主音音高”来看,D 是上方半音,C 是下方半音,依然具有镜像对称关系。需要强调的是,两个声部的镜像旋律可能造成局部区域的整体“镜像和声”,也可能仅仅是一种对位发展手法,整体和弦进行并不呈现严格镜像,这种情况可以称之为“伪镜像和弦”。
(三)错位镜像对称
辟斯顿晚期作品中,对于对称原则往往呈现出更加“现代”的处理方式。就像有一种带有凹型或凸型的镜面,会使“人形”产生“胖”或“瘦”的镜像反射结果。如果将这种“哈哈镜”的“镜像音程”变化手法用在主题旋律的写作当中,便会呈现出镜像反射前后的音程扩大或缩小。这种所谓的“对称旋律”实际上已经超出了传统“倒影”或“逆行”的范围。但是可以追溯到主题-动机音程的扩大或紧缩原则。
其一,“镜面”前后音程的一一对应状态依然存在,只不过前后对应的音程半音数呈现出+1(增加半音)或-1(缩减半音)的扩大或缩小;其二,“轴音”或“轴音程”的中心位置也会处于局部或整体的“对称”旋律中心,这一点不容更改,否则没有轴音的前后“错位”现象也将与“对称”毫无关联;其三,利用这种“错位”的“对称”写作原则,不仅能够降低单纯镜像旋律写法给旋律造成的“枯燥”感,还会将旋律中的音阶材料进一步加以扩大,轻松达到十二音的效果。这也是辟斯顿十二音技法的主要特点之一。
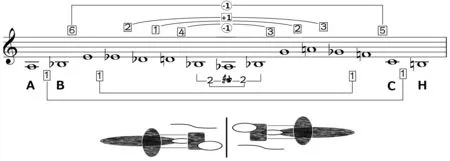
谱5 是SQ-5-I 的主题,由四个声部八度演奏。单纯从该旋律的外形来看,很难将它与“镜像”旋律的写作原则联系在一起。除了能够发现二度音程出现较多(尤其是小二度),还能发现由于旋律的半音化倾向所构成的十二音特点。但可以肯定此处不是序列写法,而是一个近似于十二音的“调性”旋律。因为对于音的强调和重复特点,以及这个乐章结尾停顿在B音上可以断定,这个乐章的调性是,⑧在辟斯顿的五部弦乐四重奏中,每部作品的各个乐章都无一例外地停顿在“主音”或“主和弦”上。谱5 这个主题也是调。
在对这个主题进行分析后,可以得出谱6 中的“错位镜像旋律”图示。所谓“错位”,是指如果以旋律中心点的为轴音——镜面,前后对应的音程会出现局部的变化,但这种变化一般只是增加半音或减去半音的状态。并且可以看出谱6下方的镜像音程半音数是对应的,尤其是旋律两端音程相等但音高已经出现半音的“错位”。中间轴音两端的音高和半音数不变,这也是辟斯顿处理“错位镜像旋律”的不变原则,如果这一点都不复存在,那么“镜像”的称谓也就名存实亡了。

谱6 《String Quartet 5-I》第1—5小节,“错位镜像旋律”图示
在谱6 上方连线中,用方框标注了轴音两端的镜像“错位”音程所相差的半音数。其中从中心向两端看,轴音左侧第二组音程(半音数4)对应轴音右侧第二组音程(半音数3⑨本文中所有半音数计算均以三全音6之内的数字表示为准,大于6的按照12-x=y公式中的y结果为准。例如此处-G的半音数实际应为9,为了音程对比更加便捷以及文字表述简明,用12-9=3的结果表示。)两对镜像音程由左向右看减少1个半音,用“”标注,谱例上方的镜像“错位音程”均按照此顺序比较。
(四)平移对称
平移对称是旋律写作中最基本的展开手法之一,模进、主题-动机的移位重复均属于“平移对称”。只不过在传统作曲技法中,移位或模进更加直观地概括了横向音高材料发展的特征,所以20 世纪前的理论家们很少用“平移对称”这样的抽象概念来称呼这种旋律发展手法。直到20世纪,大量的对称现象在作品中出现,理论家们才对所有对称现象加以总结。模进和重复作为一种具有音高材料前后对应的旋律展开手法自然也就被囊括在其中。横向音高材料的“平移”虽然看似是一种“对称”,但它更多指的是前后音高材料在发展过程中的“统一性”。因此,平移对称基本不具备有前文镜像旋律中真实而严格的“对称点”,即使有,它也仅仅是材料之间连接位置具有长音停顿或材料间有明显连接痕迹的某个音或音程,它也可以被称之为平移对称中的“虚拟轴音”。如谱7中第2行的属于旋律中的局部“水平对称”,在这两个对称的材料中间,有着明显轴音程特征的A-C-A是前后水平移位音高材料的对称位置。

谱7 《String Quartet 1-1》第64—75小节
综合来看谱7 中第2 行的音高材料,辟斯顿只是在由G 音到音的半音阶中间加入了a 和声小调的典型音列E-F--A,这也弥补了前后半音阶所缺少的E 和F 音,同时还扩展了12 个半音以外的三个音,即
如果说谱7 是整个旋律中的局部“平移对称”,那么谱8 则在两个乐句之间形成了整体的“平移对称”现象,其中第163—167 小节是第157—162 小节的上行小六度平移。由于两个旋律各自的首尾音相同,因此相连位置是FD,整个平移对称旋律的首尾音(第157 开始处与第167 小节)也是。与谱6 旋律的不同之处是,这两条旋律的音高材料相当“节俭”。前一句是-G-A-B-C,后一句是辟斯顿这么做的原因不仅仅是出于材料统一和旋律对称的考虑。将这两个平移对称旋律的音高材料加以综合,便会呈现出“交叉镜像对称音列”的现象,在此基础上,又会排列出一条以G 音为轴的镜像对称人工九声音阶,详见谱8 中的音阶图示。

谱8 《String Quartet 3-III》第157—168小节,平移对称旋律

(五)旋转对称
“旋转对称”是一种转动式的变换,从数学的角度说是围绕一个定点,每旋转一个角度后总和自身重合的图形。旋转对称是一种高度的动机化旋律发展手法。它通常形成一种两端音程半音数相等,但音高不同的旋律模式。如谱9中-B-C--D-B的旋转对称模式是由半音数为3:1:3:1:3的音程形态构成。如果将其前后四音截断纵向排列,便可以构成后文谱13 中论述的四音对称和弦。这种严格的旋转对称形态还可以在随后的旋律进行中进行填充和发展,形成一种不规则或非对称的旋律形态。如谱9最后两小节中的G也属于旋转对称形态,最后1小节中间的D音即属于填充音。有时旋转对称与镜像对称经常连接在一起构成旋律,如谱9 中最后一小节中的-G--G如果去掉填充音,便形成了镜像对称四音列,与之前的的旋转对称结合便构成了一种典型的“合成”旋律手段。

谱9 《String Quartet 2-I》第1—6小节Vl.I声部旋律
(六)对称和弦的横向铺陈
对称音程旋律通常存在于一个完整旋律线条中的局部。在辟斯顿的晚期作品中,四音列的对称音程旋律最为常见。这种对称的四音列从横向角度观察可视为主题-动机发展模式下的“展衍”,纵向罗列其四音列便会形成“对称和弦”。

谱10 《String Quartet 5-I》第1—5小节,四音组“对称音列”的集合关系
谱10 中的各音如果按相邻四音列原则划分,能够得出5 个对称音列,其中①和⑤集合相同,②③⑦集合相同,均是“BACH”动机。虽然④和⑥没有相同集合,但观察这些对称或相同的四音列集合,只有②和③之间的主音“剩余”出来。这是辟斯顿为了强调“主音”而单独安插在“非对称性”四音列中的,也正是因为这个音的存在,才形成了前文谱6中的“错位”镜像旋律。
二、纵向音高结构中的对称和弦
“对称和弦”(Symmetry chord)是指一个和弦可以分成两个部分,其中每一个部分都是另一个部分的严格倒影。⑪George Perle:Serial Composition and Atonality,6th edition,Berkeley:University of California Press,1991,p.26.由于要明确区分为两个部分,所以在论述“对称和弦”的过程中,国内外理论著述大多以四个音的和弦为基础加以论述。在传统调性和声中,一些三度叠置的七和弦便是典型的“对称和弦”结构,如C自然大调中的II7和弦D-F-A-C,下方两个音D-F 是小三度,上方两个音A-C 同样是小三度,中间的F-A 便可以看成两端小三度音程的对称“轴音程”,它是存在于和弦结构中的。从另一角度讨论这个和弦,还存在一个“虚拟”对称点——和弦结构中不存在的“轴音”G,也就是说D-F-A-C 也可以被当作“镜像对称和弦”,因为尽管G这个轴音在和弦结构中不存在,但这个对称和弦依然具有镜像的特征。同样
是对称和弦,C 和声大调的VII7和弦B-D-F-就不能算作严格意义的“镜像”和弦,因为尽管两端音程均是小三度,形成对称,但由于中间的“轴音程”也是小三度,进一步向中间推算,无法得出单一的轴音,所以,对称和弦有时会出现单一的轴音,有时则是两个中间音为小二度的“轴音程”。
在佩尔西凯蒂的《二十世纪和声学——原创样式与应用》中,严格意义的镜像和弦与对称和弦还是有一定区别的。他认为:“镜像和弦的一半是另一半精确而同步的倒影。”⑫[美]文森特·佩尔西凯蒂:《二十世纪和声学——原创样式与应用》,黄大同、杜亚雄译,上海:上海音乐出版社2009 年版,第147页。从概念中可知,和弦中的两个镜像部分是以中间明确的“相同的基础音”产生的映射(倒影),它从某种角度来说等同于“对称和弦”。比如说三个音的和弦中,增三或减三和弦也应该属于对称和弦的范畴。因此国内很多理论家会以“镜像对称”和弦来称谓“对称和弦”或“镜像和弦”也就不足为怪了。
根据以上两点概念的区分,我们似乎能感觉到,如果讨论“和弦”这个单一的纵向音高结构体,镜像与对称似乎既存在着某种区别,但又互相渗透。虽然这仅仅是一个称谓问题,但它却折射着“和声学”角度所要探讨的一个重要方面——纵向音高结构形态在横向连接法则下的相互关系。我们站在“和声学”的论述角度看,“镜像和弦”更加强调和弦结构的上、下两个层面各自的“音程同构”,它可以将各种类型的三音或四音和弦进行向上或向下的镜像倒影翻转;而“对称和弦”虽然涵盖范围较宽,也包括了镜像和弦,但它更多指代的是一个四音和弦中,上下两个声部音程同构的状态。
在分析对称和弦的过程中,我们往往过于强调“倒影”而忽略了横向和弦连接中存在的两种情况:1.连续“对称和弦”的进行中,横向的各个声部并不一定会形成倒影反向进行。从谱11 中我们会发现,第一个和弦本身只有两个音C-D,这两个音的八度重复,形成了一个2-10(2)-2 的对称和弦音结构。在随后的两个和弦中,除了中间轴音程逐渐缩小以外,外声部的两个音程均保持着第一个对称和弦的大二度核心音程性质,这四个声部始终是在同向进行。最后一个和弦是以C为轴音的五度对称和弦。
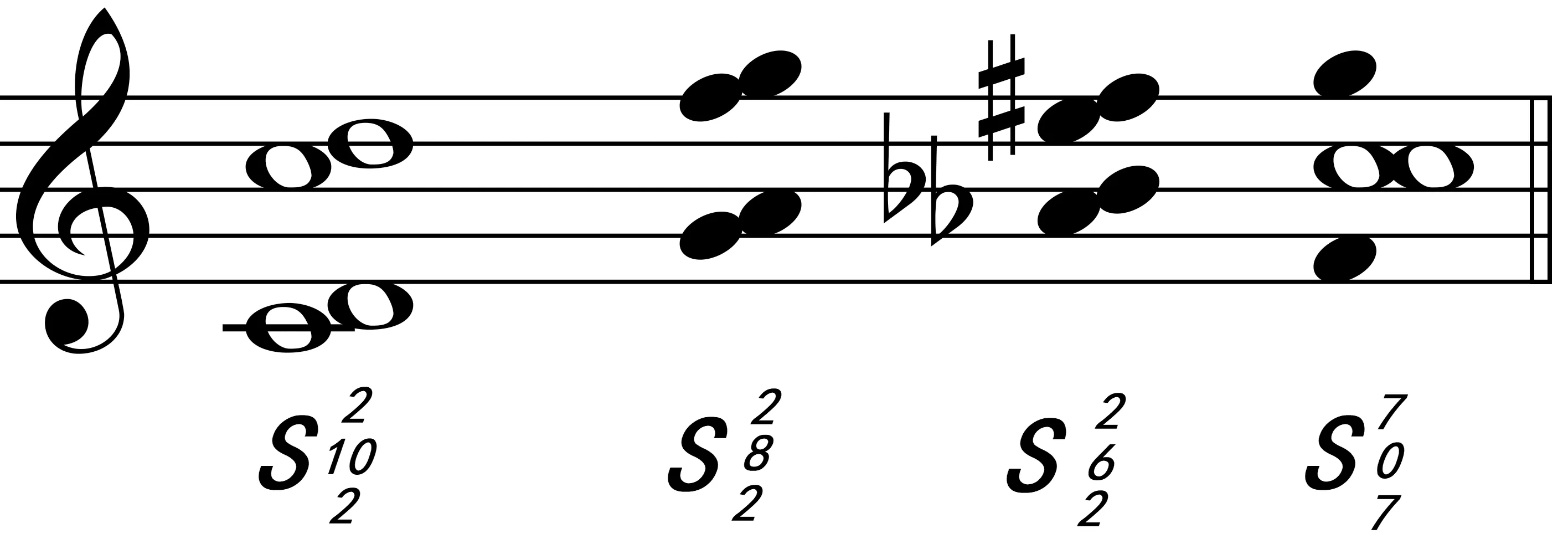
谱11 《String Quartet 3-I》第30—31小节,平行进行的对称和弦缩略图
在这四个和弦连接中,由于C 音在两端和弦中的重复使得C具有主音的作用。但仔细观察这四个对称和弦,第一个对称和弦的轴音是G,中间两个对称和弦的轴音是,第三个对称和弦的轴音是C。尽管单独看最后一个和弦,按欣德米特和弦分析原则,F 音应该是和弦的根音。但实际在对称和弦连接的过程中,单一和弦的根音可能并不是整个和弦连接过程中的“主音”。这种“轴音”的引力特征就好像调性的主音一样,是可以被人工因素影响或改变的,甚至在这种横向对称和弦的平移推动下,每个对称和弦的轴音尽管不同,但是由于在和弦连接中人为强调了C 音在首末段的重要性,所以C 作为区域主音的存在感依旧十分明显。因此,在多个对称和弦的连接中,区域性的调性主音可能是对称和弦的轴音——这些对称和弦的轴音可能相同(见后文谱13的相关分析),也可能不同。如果轴音不同,则该区域的主音就需要人工因素来加以强调,像谱11中的C主音特征便是“人工因素”影响下产生的结果。
2.“对称和弦”从广义上来说仅仅指的是和弦自身的一种严格镜像倒影形态,比如四度叠置和弦、二度叠置和弦和三度叠置和弦虽然其本身具有着对称特征,但还有可能转化成另外一种具有对称形态的音高排列方式,甚至这些和弦转位之后所形成的倒影形态很难使人联想到它本身和弦的构成原则。⑬有关“四度叠置和弦及其连接”部分的论述请参见张宝华:《辟斯顿综合调式半音体系下的非三度结构和声语言——以五部〈弦乐四重奏〉为例》,第122页。比如谱12 这个例子,方框中的对称和弦实际上是四度叠置和弦的另一种排列形式,它本身以中间E-B 纯五度音程为轴心,两端小七度音程的严格倒影形态。但结合前后和弦来看,毫无疑问它是与四度叠置和弦-B-EA 有着直接联系的,在佩尔西凯蒂看来,将其称之为四度叠置和弦的转位也未尝不可。

谱12 《String Quartet 1-III》第67—76小节,四度叠置和弦的对称和弦形态
对称和弦的形成实际上与旋律发展手法息息相关,同时它也是某些对称人工音阶中横向截断“音列”的纵向叠置使用方式。
(一)对称和弦开始的多声部倒影形态

谱13 《String Quartet 2-1》第51—54小节,对称和弦
谱13 中“人工”因素的音高材料相对来说较为统一,他们不仅在主题-动机的发展过程中起着决定性作用,在纵向音高结构中也与横向声部之间互相呼应。从谱9 的开始主题动机可以看出,动机A-C-的音程比例是3:1,在第4 小节中的3:1:3:1:3 的旋律音程连接也是一种对称关系,它是前文论述的旋律中的“旋转对称”关系(见谱9)。这种看似动机发展过程的线性旋律实际上才是20 世纪“对称和弦”的来源所在。与其说对称和弦是20 世纪的产物,倒不如说是20 世纪作曲家将古典时期的“动机发展”原则进行了“纵向音高陈列”。
谱13 中的第一个和弦是严格的对称和弦,但是随后的和弦写法则完全不是对称原则,虽然其中的两个外声部也呈现出倒影进行的状态(见谱4),但通过分析各个和弦的音程比例可以看出,每个和弦两端并不构成严格意义上的对称,因此它仅仅被视为对称和弦开始的多声部非严格倒影形态。谱14 是谱4 中两个外声部的倒影半-全音阶总结。
如前文所述,连续的对称和弦不一定会形成横向多声部的倒影形态,横向多声部的倒影形态也不一定会形成连续的对称和弦。尤其在辟斯顿的作品中,十分严格的移位或倒影只存在于局部的片段之中,因为辟斯顿始终在调性与无调性之间徘徊,所以才也会导致大量高度半音化声部叠合下的局部无调性状态。

谱14 《String Quartet 2-I》第51—54小节,两个外声部的倒影半全音阶总结
(二)对称和弦的穿插式用法
尽管对称和弦相对稳定,但对称和弦只能说是和弦的一种表面形态,因为任何半音数相同的二度、三度或四度叠置的四音和弦都有可能被看作是对称和弦,也可能以一种全新的音程结构形态构成对称和弦。比如说谱15 中第5 小节的开始和弦E-D-A-G,这个和弦实际上是四度和弦EA-D-G的一种转位形态。
在辟斯顿的作品中,和弦连接的过程中经常会穿插着对称和弦,它们通常作为一种横向旋律的总结式“纵向陈述和弦”,在连接中偶尔出现(见谱15)。

谱15 《String Quartet 1-III》第5—8小节间插性的对称和弦
如果按照欣德米特和弦分析理论对以上和弦的连续进行加以总结,会形成的根音进行。很明显,根据最后1 小节的根音进行可以看出,辟斯顿是有意形成G 调倾向的。但是从音高结构上看每小节中间声部的D 音同样有着调性主音的特征,但是与结尾根音进行所形成的GB-D 综合考量,则V-I 的和声骨架便跃然纸上。因此可以说,对于这个片段的G 调倾向,是有着明显的“人工”痕迹的。
(三)四声部严格倒影下的对称和弦
谱16 是典型的横向声部倒影形态下形成对称和弦的写法。他是在以D 音为轴的两对倒影声部进行下所形成的连续对称和弦。这种连续对称和弦在辟斯顿晚期作品中经常出现。

谱16a 《String Quartet 5-I》第9—11小节缩谱

谱16b 《String Quartet 5-I》第9—11小节轴音倒影图示

图1 《String Quartet 5-I》第9—11小节对称和弦音程图示
如果是由于线性声部的倒影形态形成的对称和弦之间的连接,“轴音”可以看成是这个片段的“主音”,其它音都在向这个轴音汇聚,并且以它作为横向进行和纵向音高结构的一种“引力极音”。
将D 音作为轴心的做法在20 世纪作曲家的作品中屡见不鲜(见图2)。“观看以下钢琴的键盘,可以发现如把D 音做为轴心,向上、下两个方向做半音性扩展,其黑键与白键的位置正好呈准确对称形态。同理,把三个黑键组的中间黑键做为轴心,向上、下两个方向做半音性扩展,其白键与黑键的位置也正好呈准确对称形态。在理论上,兰德威⑭匈牙利音乐理论家。对巴托克的轴心体系学说已有详尽的阐述,以三全音为八度内十二音均等分组的两极,并以此为轴心,作为主功能系统的互补支持音。也就是说,在键盘上由D和构成对应的两极均可为轴心。”⑯郭新:《纵向轴心镜像结构——对称思维在二十世纪音乐中的运用方式之一》,第4页。
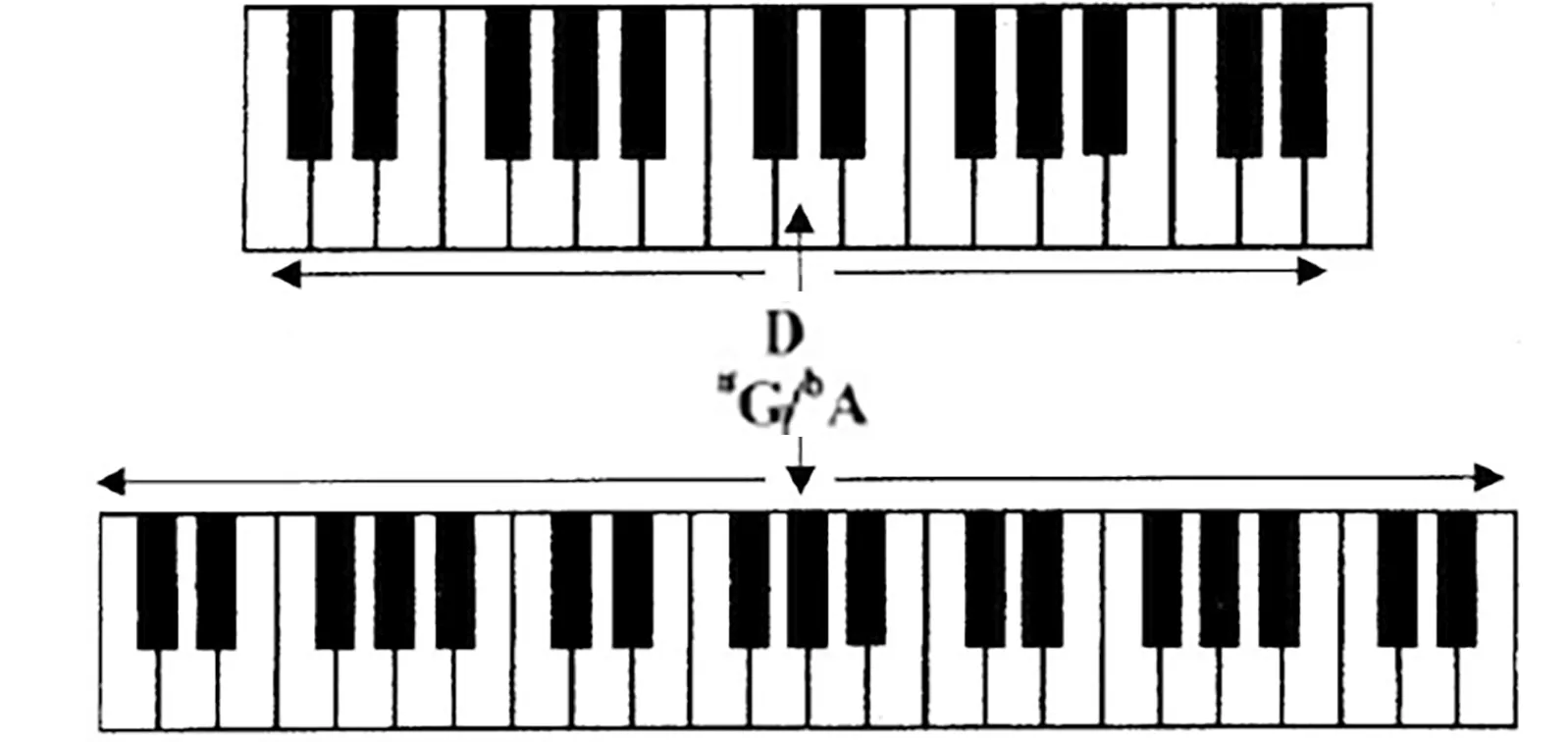
图2 D或/为轴构成的“两极”轴心图示⑮ 郭新:《纵向轴心镜像结构——对称思维在二十世纪音乐中的运用方式之一》,《黄钟》2010年第2期,第4页。

谱17 《String Quartet 3-III》第186—190小节中的对称和弦与镜像半音改动旋律
在谱17 第186 小节中,对称和弦F-G-A-B 既是对称和弦,同时也是大二度叠置和弦。这种大二度叠置和弦同时还有着全音阶的特征,和弦两端的F-B 印证了轴音D-的三全音特征。从横向线性声部的音程来看,内声部完全是两个不完全半音阶的倒影同步进行,而外声部从第186 小节开始则是音程数3-3-2-1-1-1-4-3的镜像半音改动旋律,第187 小节的D 改换为,使得半音数为3-2 的音程变为了4-1(1-4)。从调性上来看,这个片段体现了一种三全音对主音D 的支撑效果。这个片段的对称特征不仅仅体现在每一个纵向的音高结构上,横向线性声部的对称原则依然清晰可见。除了第186小节的第2个和弦由于辅助音以及最后3 个和弦要进入再现部而没有形成严格倒影的对称和弦以外,其它和弦均是在D或为轴的基础上形成的严格倒影对称和弦。
(四)四声部非严格倒影下的对称和弦
谱18 中辟斯顿处理对称和弦的情况要相对复杂一些,因为它的构成原则与上述两个例子中具有明确的轴音有所不同。尽管谱18 中的每一个和弦都形成了严格的对称形态,但是从方框中第一个非对称和弦中的A 音算起,四个声部形成了一种交叉倒影的对称形态。

谱18 《String Quartet 5-I》第173—177小节
谱19 中分为两行呈示了四个声部的非严格倒影形态,其中第1 行中的两个声部为中音与低音声部的倒影形态;第2 行呈示了高音与次中音声部的非严格倒影形态。实际上一直到中间标注“换列”的位置,其音程形态都是大致相同的,除了第4—5 音位置出现的2 和1 的“非严格”倒影形态,其余位置均是严格的。但是从“换列”位置开始,根据上下两端标注的半音数可以看出,第1 行后半部分是两个内声部,第2 行后半部分通过换列变成了两个外声部,其音程形态几乎是呈现出+1(增加一个半音)的状态,即两个外声部的横向线性声部音程数(第2 行后半部分)要比两个内声部的线性音程进行多1 个半音。辟斯顿如此处理就使得对称和弦的构成因素复杂了。
首先会有一种疑问,为什么选择中音与低音声部进行配对,既然前七个音的倒影横向音程形态基本一致,为什么不选择中音声部与低音声部的非严格的倒影形态,而省去中间部分换列的麻烦。这种组合方式是笔者经过多次尝试后才最终绘制的图示,也许能力有限,其中还有其它的玄机没有发现,但是根据多次尝试,只有按照如下方式才能得出这个非严格倒影片段中较为持久的轴音——A。并且按照此换列结合的方式,我们能够看到谱19 第1 行的首尾音均是A,这也是此区域片段的主音。中间换列位置的与A实际上依然是一种三全音的支撑关系,只不过它已经不是上例那种存在于键盘之上可以直观可见的“自然音”对称形态。这已经是的一种人工移位状态。
其次,我们在进行某部作品的局部片段和声分析时,应该本着一种联系的角度。纵观所有涉及到SQ-5-I 的谱例,从之前论述的“错位镜像旋律”(见谱6)到本节论述的大量的对称和弦,再到SQ-5-II 乐章中所运用的“12 音调性序列”⑱张宝华:《论辟斯顿〈第五弦乐四重奏〉第II乐章的调性序列和声手法》,《乐府新声》2019年第4期,第55页。。我们似乎感觉到辟斯顿在最后一部弦乐四重奏中的“躁动”和不安。尽管这首作品所使用的一些技法在之前几部弦乐四重奏中也曾经出现过,但就对称和弦而言,SQ-5-I中使用得最多,也最复杂。从某些段落看,它已经趋于无调性的写法。
(五)平移对称音阶下的对称和弦
从谱20 中,我们可以看到SQ-4-IV 中Vl.I 声部的1:1:3 平移对称人工音阶模式下的非连续性对称和弦进行。

谱20 《String Quartet 4-IV》第48—52小节⑲ 谱例中的S代表对称和弦之意,S字母为英文“symmetry”(对称)的首字母。
从谱20 中可以看到,第51 小节是非对称性和弦,其余四个小节中均使用对称和弦。这些对称和弦主要可以分为两种类型:①内声部与外声部互为倒影形态所构成的对称和弦,如第48—50小节中的对称和弦均属于此类,这类对称和弦有着对称音程流动性的变化特征,其具体变化情况会随着动机展衍的音程距离有所变化;②四声部同向平行移动,纵向音程不变,如第52 小节,这种对称和弦的纵向和声紧张度不会变化,其和声张力完全是在横向音程变化的推动力下产生。
图3详细列出了谱20中每一个小节第一拍的音高结构,其相互之间的音程含量变化一目了然。四个声部之间每一对横向相连的音程都有着极其缜密的音程递增和递减规律,在此基础上才会进一步形成每一小节对称和弦的不同音程形态。
图3 《String Quartet 4-IV》第48—52小节各声部强拍之间的音程涵量图示
首先,从纵向音程变化的角度观察,左边第1列音程涵量形成了半音数为5-4-2-1 的递减模式,其中上方音程5-4和下方音程2-1分别形成-1状态;中间音程4-2 形成-2 状态。左数纵向第2列音程形成0-2-4-6 递增半音数2 的排列状态。左数第3列形成递减半音数2的排列状态。最右方的纵向音程形成5-5-4-3 的递减半音音程状态。这种纵向音程比例的递增与递减模式,是导致谱20 中对称和弦纵向对称音程产生变化的主要原因。
其次,再观察横向声部中每一小节模进音组之间的音程变化,会发现其各自运行的轨迹并不相同,其中两个外声部中标注方框的位置是连续两小节的重复音组。每一个线性声部的横向进行都担负着整体对称和弦移动过程中的横向和声推动力。
再次,该例的写法并不单纯是和声性思维,其中还巧妙运用了某些“线性对位”的原则。
最后,图3 中可以清晰看到,辟斯顿将高音声部纯四度模进过程中的核心音程,精心编织成一张网状结构,形成四个声部之间的隐性音高结构力。
结 语
对称性是审美本能的一种表现,它存在于自然界与人类社会活动中,各种物象的形体以及无数事物的运动形态,甚至在音响世界里几乎都存在着对称与平衡。“动植物的形体是对称的;晶体中原子的排列是对称的;许多自然现象和物理现象,从钟摆摆动的轨迹到天体运行的轨道,都是对称的。……20世纪的某些西方作曲家,曾试图打破对称原则,但从整个发展趋势看,这种对称原则在20 世纪不但没有削弱,反而加强;这是理性主义在现代音乐中的重新抬头,而且变本加厉的结果。”⑳钱仁康:《音乐语言中的对称结构(一)》,《音乐艺术》1988年第2期,第40页。
复调音乐中,倒影卡农或多个声部之间的严格倒影形态是典型的“镜像对称”思维。由于镜像对称写法容易破坏音级进行的倾向性,影响调性功能和声连接的逻辑规律,所以在古典时期,除了一些赋格段或卡农段落以及少量展开部,还偶尔可以见到局部严格的镜像对称以外,严格的多声部音高结构的“对称思维”几乎濒临灭绝。直到浪漫派晚期,肖邦、李斯特、沃尔夫的作品中,这种“对称思维”才又重新被作曲家们所重视。
“音高结构的对称形态”是辟斯顿弦乐四重奏作品“综合调式半音和声体系”㉑张宝华:《辟斯顿综合调式半音体系下的非三度结构和声语言——以五部〈弦乐四重奏〉为例》,第122-131页。研究的一个分支,亦是“人工音阶运用”㉒张宝华:《辟斯顿弦乐四重奏作品中的人工音阶类属及运用方式》,《中国音乐学》2019年第2期,第125-134页。方面研究的进一步延伸。本文对于辟斯顿弦乐四重奏中线性声部的音高对称形态研究与纵向音高结构对称形态研究是相辅相成的,线性对称是纵向“对称和弦”研究的前提和基础。通过分析可以看出,辟斯顿在横向声部中所运用的很多音高对称现象,会直接或间接地体现在纵向音高结构上。在20 世纪的大量新调性音乐作品中,都存在横向或纵向音高材料的镜像对称现象,它们之间往往互相影响并彼此支持,但除了技术上,我想更多的是一种美学角度的平衡与制约。希望本文的研究能够对进一步深入了解辟斯顿作品的音高结构,把握其个性化的新古典主义风格有所裨益。
