培养学生审辩式思维的实践与思考

【摘要】本文论述在小学数学课堂中培养学生审辩式思维的方法，建议教师营造积极的审辩氛围，贮备丰富的学科知识，开展真实的审辩活动，从而促进学生思维能力的发展。

【关键词】小学数学 审辩式思维 审辩活动

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2020）45-0057-03

审辩式思维是当下教育领域公认的人类三大必备能力之一，也是中国学生核心素养中关键能力的核心部分。数学是对客观现象的抽象和概括，在数学课堂教学中引导学生追求基本知识、获得基本技能、形成求证态度的过程，可以作为培养学生审辩式思维的重要载体。

小学生的发展有其自身的特点，他们的认知发展处于从具体运算向形式运算过渡的阶段，有一定的探究意识，能对抽象的概念实现逻辑性操作，但思维活动需要具体内容给予支撑;他们的学习动机由附属内驱逐步向认知内驱发展，由崇信权威的主张逐步过渡到相信自己的理解。基于上述特点，通过实践与反思，笔者认为要培养小学生的审辩式思维需做好以下几方面工作。

一、营造积极的审辩氛围

（一）培植敢于质疑的民主关系

质疑是审辩的起点。亚里士多德说“思维是从疑问和惊奇开始的”，有了问题人才会主动思考，有了问题审辩才会展现价值。问题是主体认知与情境信息的冲突，问题意识的实质是对原认知与新信息之间差异的敏感，这种敏感源于个体强烈的自主意识。要培养学生的质疑能力，首先需要建立起学生的自主意识，民主关系是建立这种意识的重要手段。

笔者在小学数学课堂教学中主要采用以下策略培植学生的民主关系、涵养自主意识：一是充分利用教科书中的“判断对错，然后修改”等题型，让学生从评判者的角度对问题进行审视，使学生看待问题的视角发生变化，确立主体意识。二是利用“轮值小老师”模式，让学生借助合作学习小组平台，给小组成员“讲授新课”和“分析易错题”，让学生轮流体验“师”“生”角色，理解角色特点，拉近角色距离。三是通过“追求事实的数学家”“大科学家也犯错”等主题故事，建立尊重事实、不迷信权威的民主文化，逐步培植学生自由的学术思想和严谨的举证态度。

多元视角、多元身份以及以事实为依据的价值判断是形成民主关系的重要手段，教师要充分发掘身边的资源，为民主文化建设提供更多的实践活动，进而为学生养成敢于质疑的习惯打下坚实的心理基础。

（二）培育乐于求证的探究意识

审辩式思维教育的目的是引导学生发展其认知和思考的深度与广度，而不是给他们所谓的正确的答案和结论。[1]从这个意义上说，解决问题的实质是促进学生认知能力和思维能力的发展。能力不同于知识，不能靠教师的“喂养”和学生的死记硬背获得，它需要学生在自主探究的过程中，借助挖掘、识别、推理、归纳、运用等实践方式逐步积累。学生乐于自主探究的态度，决定了审辩式思维能力发展的速度。

好奇心和好胜心是激发学生自主探究的关键动因，在课堂教学中，教师可以借助这“两心”调动学生自主探究的积极性。比如在教学苏教版数学教材四年级下册《三角形内角和》的内容时，首先，笔者给每一名学生发一个同样的三角形，提问：“我想知道这个三角形的内角和是多少度，该怎么做？”学生几乎齐声回答“量”。学生测量和交流后，得出的结论是180度。其次，笔者出示几种不同的三角形，让学生猜测：“不同形状的三角形的内角和可能是多少度？”这一猜测活动激起了学生的好奇心，他们发言踊跃、观点不一。测量后统计数据，发现不同形状的三角形的内角和都是180度，这使学生的好奇心进一步激发。笔者顺势提出：“谁有办法不借用测量的方法也能证明三角形的内角和是180度，谁就是我们班的数学小博士。”学生的好胜心被点燃，无需提点，讨论、实验、资料查询等指向问题解决的探究性工作就开始了。最后，学生通过自主探究，用撕、画、折、拉等方式证明了所有三角形的内角和都是180度。

好的教学设计应该促进学生主动地生长，易于生发学生兴趣的问题和便于学生探究的学习内容，能够激发学生的探究意识，学生的审辩式思维也会在自主探究中得到提高。

（三）培养善于审辩的理性气质

审辩式思维是“对问题进行澄清、分析、评价和进行论证的”过程，[2]它追求证据的真实性、论证过程的逻辑性和结论的合理性。在教学过程中，教师要将此作为引导学生进行审辩的依据，要求他们以理性的方式对待问题，而不是以简单的“是”或“否”作为审辩的结论。

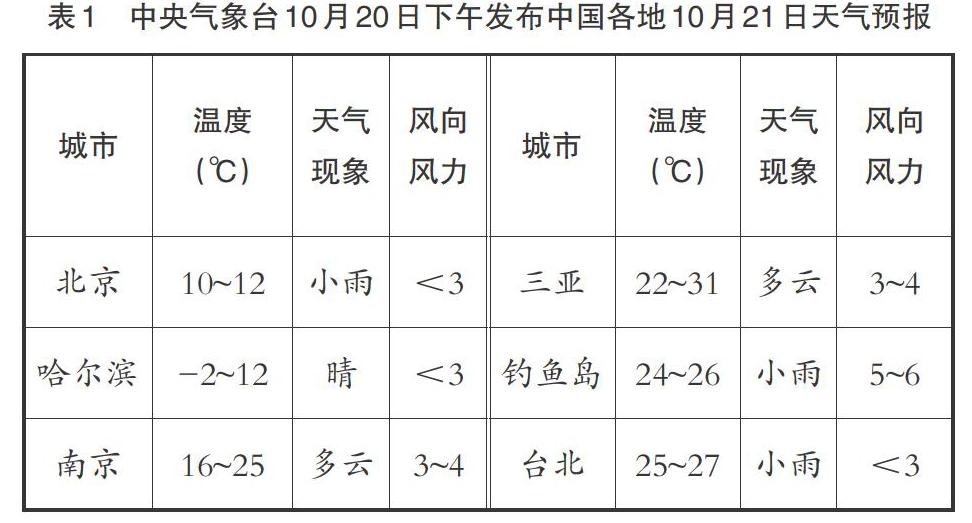
比如，在教学苏教版数学教材四年级上册《可能性》的内容时，笔者利用审辩三部曲——“条件观察、逻辑推理、实验证明”，帮助学生建立“可能”“一定”“不可能”等概念。第一步，看清球的颜色种类及各色球的个数;第二步，对摸出的球的色彩进行逻辑推理，明确要求学生说出推理过程;第三步，摸球查看，通过多次实验，以事实论证学生推理的合理性。在巩固实践环节，笔者设计开放型推理题型，让学生分析：北京、哈尔滨和台北的小朋友在10月20日可能穿什么样的衣服？开始笔者不提供任何参照信息，不少学生天马行空，组内结论差异明显，从假设条件到推论过程似乎都很合理，但又没有更好的理据说服对方。随后，笔者根据学生的需要，下载新华网上相关的天气信息供学生参考（见表1）。有了实据，学生的推理准确性提高了，争辩也相对减少了。

表1 中央氣象台10月20日下午发布中国各地10月21日天气预报

实践“审辩三部曲”能很好地培养学生的理性气质，能让学生明白真实证据、合理推论的重要性。同时，也能让学生体会到，现实中常常不存在唯一正确的答案，要学会理解与尊重他人的观点。

二、贮备丰富的学科知识

审辩式思维是有目的的、不断自我调整的判断。[3]在课堂教学中，学生对信息的判断主要以学科知识为依据。学科知识是小学阶段的重要学习任务，也是学生思维发展、能力提升的重要纽带。在课堂教学中，教师应当注重学科知识的积累，以知识的丰富性助力学生审辩式思维能力的发展。

（一）积累概念型知识

概念是事物特有属性的信息表征，是人类认知事物的关键凭据。在课堂教学中，教师应帮助学生积累学科概念，丰富其内涵和外延，并通过适当的训练提高学生的辨识能力和应用能力。

比如，在教学“互质”概念时，为了方便学生快速识别两个数是否互质，在教学过程中，教师除帮助学生理解基本概念“公因数只有1的两个自然数，叫互质数”，还可以引导学生进一步归纳一些特殊的互质关系，如：相邻两个自然数互质、相邻两个奇数互质、两个不同的质数互质，等等。

积累丰富的概念型知识不仅可以加深学生对基本概念内涵的理解，还能够使概念的外延与内涵之间产生链接，为识别信息、挖掘特征、解决问题提供更宽广的路径。

（二）强化关系型知识

审辩式思维始于问题产生，终于问题解决，在始与终之间需要架设一座桥，这座桥就是已知条件与未知条件之间的关系。在数学学科中，能在学生分析与推理的过程中起到关联性作用的内容主要有：等量关系、不变量、面积守恒、比例及其他定理定律。在课堂教学中，教师可以引导学生运用这些知识，育植“贯通”“转化”思想，提高解题效率，增强解题趣味。

比如，在教学苏教版数学教材六年级下册“圆柱与圆锥”单元时，笔者设计了一道借助关系型知识解决问题的练习：一个圆柱与一个圆锥高度之比是6∶5，圆锥半径是圆柱半径的五分之三，圆柱的体积是30立方米，求圆锥体积。这类题目如果用传统的计算方法难度较大，笔者引导学生观察条件特征，追求关联信息。最终，学生借助比例等值建立主体关系式，将圆柱与圆锥的计算关系式构建到一个比例中去：[13×3×3×5×π5×5×6×π=][圆锥面积30]，而后学生又利用商不变规律整理等式，利用“削削乐”让计算变简单：[13×3×3×5×π5×5×3×2×π=][圆锥面积30]。

这个例题的设计，重点在于强化学生利用关系型知识解题的意识，让学生在实践过程中体验关系型知识带来的便利与乐趣，为学生审辩式思维的发展带来新的思路。

（三）整理策略型知识

有些数学练习题的数量关系比较复杂，除需要概念型知识、关系型知识作为支撑，还需要一些特殊的策略帮助。小学阶段的解题策略主要包括：列表、假设、画图、枚举、转化、代换等。这些策略型知识的学习穿插在不同年级，在课堂教学中，如果能够时常引导学生对策略型知识进行整理，不仅能加深学生对知识的理解，对学生审辩式思维能力的提高也有帮助。

比如，在教学苏教版数学教材六年级下册“用假设策略解决问题”时，笔者将四至六年级教材中出现的相关内容一起呈现，引导学生自己梳理、寻找方法。教学中，笔者出示了3道题目。例1：小宇和小丽共有72支铅笔，小丽比小宇多12支。两人各有铅笔多少支？例2：小宇和小丽共有72支铅笔，小丽给小宇12支后，两人一样多，两人各有铅笔多少支？例3：鸭和兔共20只，有腿50条，鸭和兔各有多少只？前两题是已经学过的内容，稍加审辩，学生就能根据题目特征选定策略解决问题。新授的内容，有了策略经验，学生迁移起来也比较容易。

整理策略型知识，可以使学生进一步理解常用策略的本质、把握每种策略的运用范围和要点，为他们更快、更好地解决问题提供帮助。

三、开展真实的审辩活动

审辩式思维能力的发展不是一个“被教会”的过程，它是学生在实践的过程中借助自己的观察、分析、综合、判断、表述等活动而生长出来的力量。在教学实践中，笔者一般采用以下方法促进学生审辩能力的提升：

（一）指向信息收集的“圈划注画”

审辩的主要任务是抓捕信息、厘清思路。为此，在学生解题时，笔者要求学生用“划”标出重要条件，用“圈”标出条件关系，用“注”标明信息内涵，用“画”厘清解题思路。

例：

“圈划注画”等操作，能促使学生的“审辩”行动真实开展，也使思维的过程可视化，为学生找到合适的解题路径带来方便。

（二）指向路径拓展的“一题多解”

一题多解指鼓励学生用不同策略解决同一个问题。在实践操作中，笔者一般设计“自解”“互赏”“同评”三个环节，引导学生一题多解。

比如，在教学“租船”问题时，笔者先提出“算一算，谁能解决这个问题”，放手让学生用自己擅长的方法解题。接着，笔者提出“比一比，哪个小组解题方法最多”，用竞赛形式引导学生对不同的方法进行探索，发散学生思维。最后，笔者追问：“这些方法有什么相同或不同的地方？它们的优点各是什么？你最喜欢哪种方法？为什么？”这些指向分析与评价的提问，可以促使学生进一步了解不同策略的特征，深入思考策略的使用范围。

一题多解能够引导学生从不同层次、不同角度、不同思路去审辩信息、思考问题。这有助于激发学生合作、探究、争辩与交流的热情，也使学生思维的灵活性及综合性得到提高。

（三）指向结论丰富的“一问多答”

学校教育的目的是培养能够适应社会生活的人，复杂的社会问题并不存在唯一的“真理”。因此，在课堂教学中，教师应当选择结论丰富的题型，引导学生从不同角度探索可能存在的答案，以此培养学生辩证看待问题的习惯。

例如，在教学路径选择问题时，笔者出示了如下题目：

小组讨论：宁宁去学校可能会走哪条路？为什么？

通过研讨，学生给出以下答案：1.宁宁从中间那条路直接到校，因为这条路最短;2.宁宁可能会先到洋洋家，再和洋洋一起结伴上学;3.宁宁也可能先去商场，他或许要买些学习用品……面对这些富有创意的回答，笔者给学生点赞。这种基于生活现实的考虑，不仅拓展了学生的思维空间，也丰富了他们的生活阅历。

总之，在小学数学课堂教学中，教师应打造积极的思维环境，让学生在知识的学习中、在问题的探究中、在实践操作与理性思辨中，逐步形成“不懈質疑，包容异见，力行担责”[4]的审辩思维。

【参考文献】

[1]刘葳.审辩式思维能力的培养与训练[J].内蒙古教育，2014（19）

[2]谢小庆.审辩式思维能力及其测量[J].中国考试，2014（3）

[3]谢小庆.审辩式思维[M].上海：学林出版社，2016

[4]谢小庆，刘慧.审辩式思维究竟是什么[N].中国教师报，2016-3-16（4）

作者简介：杨伟忠（1971— ），江苏无锡人，大学本科学历，一级教师，江阴市南闸中心小学校长，研究方向为审辩式思维课堂文化、学生数学素养的发展。

（责编 雷 靖）