尖锥形后备齿PDC钻头的参数优化与现场应用

2020-03-09姚建林李伟成李德伟杨开雄

钻采工艺 2020年5期

姚建林, 李伟成, 李德伟, 冯明, 杨开雄, 肖洋

(1四川川庆石油钻采科技有限公司 2中石油川庆钻探工程有限公司钻采工程技术研究院 3中石油川庆钻探工程有限公司长庆固井公司 4中石油川庆钻探工程公司 5中石化西南石油工程有限公司重庆钻井分公司)

为了提高PDC钻头在各类难钻地层环境中的破岩效率并延长其使用寿命，国内外研究学者和相关工程技术人员做了大量的工作，在一定程度上提升了PDC钻头的综合性能[1-3]。其中，美国Novatek International公司的Durrand等人发明了一种尖锥形PDC切削齿[4]，为提高PDC钻头在难钻地层中的抗冲击性、侵入性和寿命提供了新方案。此后，美国Novatek International公司的D. R. Hall等人研制出了以尖锥形PDC齿为主要切削元件的PDC钻头，并通过多组室内实验验证了其破岩效率突出，平均机械钻速可达到21.33 m/h[5]。虽然，尖锥形PDC齿的侵入性较强、破岩效率高，但以其作为主要切削元件在研磨性较强、可钻性差的难钻地层中长时间工作时，在单位时间破岩量较小、破碎比功较大，且尖锥形齿因持续刮削岩石而磨损进而被磨钝，使其失去强侵入性的优势，从而导致整个钻头的破岩效率降低[6]。

本文通过ABAQUS有限元方法计算分析了尖锥形齿的切削力和破碎比功，并寻得了尖锥形齿的最佳切削工作参数。基于此，研制出以尖锥齿为辅助切削元件，常规平面PDC齿为主要切削元件的Ø215.9 mm PDC钻头，并在岳X井成功开展了现场试验，试验结果表明该钻头综合性能优秀，能有效地提高钻井效率、降低钻井成本。

一、尖锥形齿的破岩机理

在本文研制的尖锥形后备齿PDC钻头中，尖锥形齿作为常规平面PDC齿的辅助切削元件，其破岩过程的运动状态与常规平面PDC齿相同，即在钻压(轴向力)和扭矩(周向力)的作用下破碎岩石，然而由于几何形状差异，同样的运动又导致了截然不同的破岩过程：常规PDC齿主要以 “刮切”为主，通过齿与岩石接触区域的高比压产生的剪切作用破坏岩石；尖锥形齿则侧重于“犁削”，拉应力起到了破岩的主要作用，其破岩过程分解为四个阶段：①岩石变形阶段；②岩石裂纹产生阶段；③岩石拉应力极值带延伸阶段；④裂纹贯通及岩石块体崩落阶段。

二、尖锥形齿的工作参数寻优

1. 尖锥形齿的主要工作参数

在尖锥形齿的工作过程中，影响其破岩效果的参数有齿顶角θ、齿顶半径r、安装参数前倾角α，如图1所示，其中D为齿直径，H为齿高。

图1 尖锥形齿的主要工作参数

2. 单齿犁削破岩过程仿真

考虑到不同齿顶角和前倾角均是影响尖锥形齿破岩效果的主要因素，而且匹配不同齿顶角的最佳前倾角也不一定相同，因此本仿真过程中一共有θ和α两组变量，通过对齿顶角和前倾角的不同组合进行联合仿真，得出不同参数条件下的单齿切削力和破碎比功，并以此为依据找到各种参数组合中的最优方案。

2.1 模型假设

尖锥形齿的随钻头旋转-进给的复合运动简化为恒定速度、固定吃深的直线运动；不考虑齿的磨损，忽略温度、围压和钻井液的影响。

2.2 几何模型

根据目前工程应用中常用的齿形参数，将尖锥形齿直径设置为13.44 mm。齿顶角θ分别取60°、75°、90°和105°；取齿顶半径r为2 mm,在作单齿破岩分析时，将前倾角α控制在-30°～﹢20°之间以寻求其最佳角度，分别取α=-30°、-20°、-10°、0°、10°和20°。根据实际工作状态，取单齿吃入深度为2 mm。同时为避免边界效应仿真结果的影响，根据圣维南原理，将岩石模型设置为40 mm×30 mm×15 mm的立方体模型。

2.3 材料模型

由于本次仿真主要考虑单齿在破岩过程中的破碎比功，忽略齿本身的微小形变，将尖锥形齿设置为刚体。岩石材料选为灰岩，本构关系选用D-P 准则，并定义了硬化特征[7]和设置损伤演化系数。岩石模型的主要材料参数见表1。

表1 岩石模型主要材料参数

2.4 网格设置与接触定义

本次仿真采用ABAQUS有限元仿真分析软件，选用六面体网格。采用弹性滑移的罚函数公式，切向摩擦因数取0.4,接触关系采用“硬接触”方式。

3. 单齿犁削破岩仿真结果分析

单齿犁削仿真破岩过程如图2所示。通过改变齿顶角参数θ和前倾角α重复上述仿真过程，得到了不同的θ角(共4种)和不同的α角(共6种)总共24种组合条件下的尖锥形齿破岩过程所需的切削力随时间的变化规律。

图2 单齿犁削仿真破岩过程

根据上述仿真得到的24组切削力数据，可计算出各θ-α组合条件下的平均切削力，即：设定每个固定时间间隔输出切削力数据，提取此历史输出数据并求取其平均值，其大小即能表示某个θ-α组合条件下的切削力大小。

图3 平均切削力随齿顶角θ和前倾角α的变化

根据计算数据可得到全部24组仿真所得的平均切削力随θ和α的变化曲面图，如图3所示。以24组θ-α组合及其对应的切削力结果为基础，通过Matlab曲面拟合即得到了切削力随θ和α平滑变化的结果。

图3表示平均切削力随θ和α变化趋势。由图3可知，θ=60°时切削力整体趋于最小，即在此条件下尖锥形齿破岩所需的扭矩最小，这是因为60°锥顶角的PDC齿要比其余角度条件下的齿更锐利，因而“省力”。随着前倾角α增大，平均切削力先减小后增大，在α=-10°附近，切削力取得最小值(各锥顶角情况均类似)；随着锥顶角θ的增大，平均切削力总体呈上升趋势，在前倾角-10°≤α≤-5°这个区间内，锥顶角θ对平均切削力的影响不明显，在其余的α区间，锥顶角θ均会明显影响平均切削力。因此，在锥顶角要求较大时(对抗冲击性要求较高时)前倾角应优先选择在-10°～-5°的区间内。

此外，为了求取各种情况下的破碎比功，还需在仿真破岩的过程中记录破岩体积和能量消耗，在得知切削体积的情况下，根据各齿所消耗的功(通过切削力随位移变化积分可得)即可计算出各θ-α组合条件下尖锥形PDC齿的破碎比功，通过仿真得到破碎比功随θ和α的变化曲面图，如图4所示。

图4 破碎比功随齿顶角θ和前倾角α的变化

以24组θ-α组合及其对应的破碎比功结果为基础，通过Matlab曲面拟合即可得到破碎比功随θ和α平滑变化的结果。

图4表示了破碎比功随θ和α的变化趋势。由图4可知，θ=60°时切削力整体趋于最小，这与切削力的变化规律类似，说明相比破岩体积，切削力才是影响破碎比功的主要因素。随着前倾角α增大，破碎比功先减小后增大，在α=-10°附近，破碎比功取得最小值(各锥顶角情况均类似)；随着锥顶角θ的增大，破碎比功总体呈上升趋势，在前倾角-20°≤α≤0°这个区间内，锥顶角θ对破碎比功的影响不明显，而在其余的α区间，锥顶角θ均会明显影响破碎比功。综合切削力和破碎比功随齿顶角θ和前倾角α的变化规律可知，θ=-10°，α=60°为尖锥形齿最佳的破岩工作参数。然而，较小的锥顶角虽然“省力”又“省功”，但是会削弱切削齿的抗冲击性，影响其寿命，因此在实际应用过程中，应将前倾角控制在10°≤α≤-5°这个区间内，从而获得更大的锥顶角调整空间，以兼顾切削力、破岩效率和寿命之间的平衡关系。

三、尖锥形后备齿PDC钻头现场试验

在吃入深度相同的条件下，尖锥形齿受到的切削力小于常规PDC齿。较小的切削力可减小钻头扭矩和由扭转振动产生的周向冲击，因此常规钻头上引入用尖锥形齿可提高钻头的抗冲击性能。但由于破岩机理的差异，尖锥形齿在吃入岩石能力方面不如常规PDC齿，且其磨损速率高于常规PDC齿[6]。因此实际工程应用中，采用了尖锥形齿作为后备齿的形式对现有的常规PDC钻头作了改进。

在钻头的工作初期，作为主切削齿的常规平面PDC齿高于尖锥形齿，且由于其齿刃锐利、吃入岩石能力强，此时钻头主要以平面齿切削为主，当主切削齿逐渐磨损后，作为后备齿的尖锥形齿逐渐出露，并以犁削的形式在井底形成犁削槽，同轨或其轨道附近的平面齿再进行破岩时，由于有尖锥形齿对岩石的预先破碎作用，使得主切削齿能有效侵入并破碎岩石，从而提高钻头在磨损之后的破岩效率。

图5 尖锥形后备齿PDC钻头

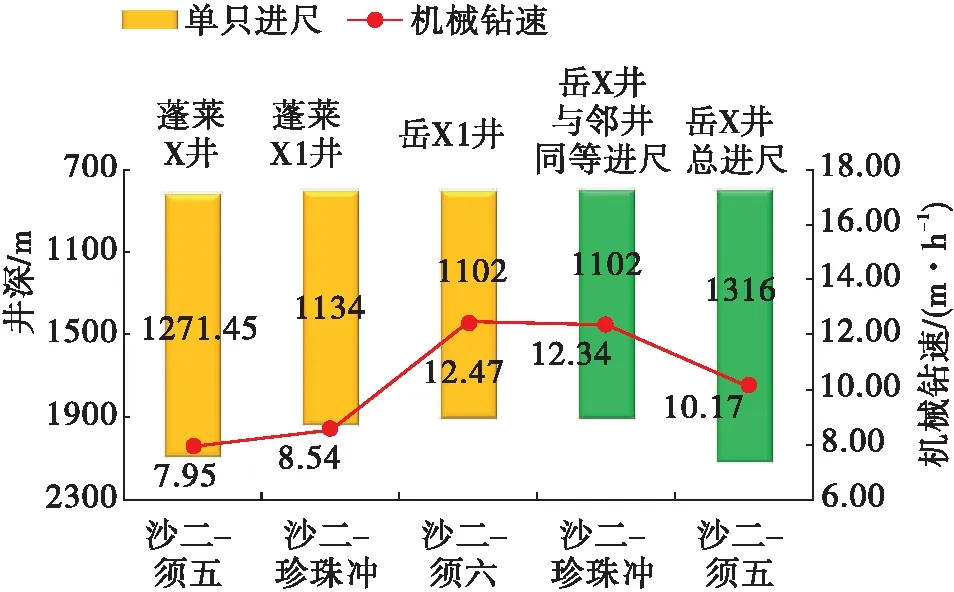
图6 岳X井与邻井同等条件下使用对比图

本文在上述角度优化分析和常规PDC钻头的结构特征的基础上，研制出以尖锥齿为辅助切削元件，常规平面PDC齿为主要切削元件的Ø215.9 mm PDC钻头，如图5所示。在岳X井试验结果表明,该钻头在机械钻速和总进尺方面表现优异，如图6所示。其中，单只钻头进尺1 316.6 m，一趟钻从沙二钻至须五，平均机械钻速10.17 m/h。同比邻井岳X1井常规平面PDC钻头，单只进尺多214 m，平均机械钻速相当。