水下双阵列拖曳系统缆破断情况下的运动响应

王 飞， 涂卫民， 邓德衡， 吴小峰

(1. 上海交通大学 海洋工程国家重点实验室， 上海 200240； 2. 上海交通大学 高新船舶与深海开发装备协同创新中心， 上海 200240； 3. 武汉第二船舶设计研究所， 武汉 430064； 4. 中国船舶科学研究中心， 江苏 无锡 214082)

在现代海洋开发、水声探测及深潜遥控无人潜水器(ROV)等诸多领域，水下拖曳系统有着十分广泛的应用[1-2].双阵列拖曳系统作为一种现代高速重载系统，在海上运行过程中，不可避免地会受到各种外界干扰，特殊情况下拖缆可能会因碰撞、缠绕、快速机动而意外破断，破断时系统会产生较大的冲击响应，此后系统可能仍可部分工作，也可能引起连锁反应或二次破坏，以致整个系统损毁.针对此问题，本文主要围绕水下双阵列拖曳系统，展开数值模拟研究，探讨阵列缆在破断时的瞬态响应以及破断后的运动响应，为系统的设计与应用提供参考数据.

对于水下拖曳系统动力学，国内外学者基于各自的研究目标，通过建立运动数学模型，采用数值模拟等方法来研究其在不同情况下的稳态[3]及动态运动响应特性[4-14].现在广泛采用的方法包括有限差分法、集中质量法等，它们能够很好地预报拖缆系统在正常状态下的运动.Ablow等[5]建立了有限差分法，该方法可大时间步长求解，效率较高；Huang[6]提出了集中质量法来计算拖缆的动态运动响应.在此基础上，国内外众多学者展开了卓有成效的研究[7-14]，内容涉及诸多方面，比如弯扭影响研究[7]，系统收放模拟[9-10]，水下拖体耦合动力学研究[13]，导流缆系统运动研究[8]，水面母船耦合影响研究[11-12,14]等.

拖缆破断发生的概率小，因而针对其响应的研究很是有限.特别对于多阵列系统，阵列缆破断后系统的对称性遭破坏，其运动响应将变得复杂，难以直接分析.本文针对水下双阵列拖曳系统，在给出时域内系统运动数学模型及拖缆破断数值实现方法的基础上，采用数值模拟的研究方法，展开细致的研究，模拟计算系统在不同机动条件以及不同缆位置破断时的运动，分析其瞬态响应及后期运动响应的特性.

1 控制方程

本文考虑的双阵列拖曳系统为高速系统，为简化问题，将拖缆(牵引缆和阵列缆统称为拖缆)视为理想的柔性缆索，同时忽略缆对水面拖曳母船的耦合作用.

图1所示为双阵列系统示意图，由牵引缆A，2个阵列缆B、C及一个水下拖体组成.对于每一根拖缆(阵列)，s为缆长坐标，S为其总长.水下拖体的姿态角分别为：艏向角ψ，为艏向水平偏离y轴的角度；俯仰角ϑ，抬艏为正；横倾角φ，右倾为正.欧拉角θ,φ为拖缆在惯性坐标系下的姿态角，仅取决于缆的空间位置，其取值范围在本文中定为

(1)

图1 水下双阵列拖曳系统示意图Fig.1 Schematic diagram of underwater dual array towed system

1.1 坐标系统

为描述整个系统的运动建立3个坐标系统，惯性坐标系(xyz)，拖缆局部坐标系(btn)以及拖体运动坐标系(ξηζ).其中惯性坐标系原点位于水面，z轴垂直向上；拖缆局部坐标系附于拖缆上，t轴为缆切向，n为法向，b为侧法向；拖体运动坐标系随拖体运动，ξ轴指向艏向，η轴指向右舷，ζ轴指向下方.这3个坐标系通过姿态角相互关联，其转换关系为

(2)

式中：A为拖缆坐标系转换矩阵，

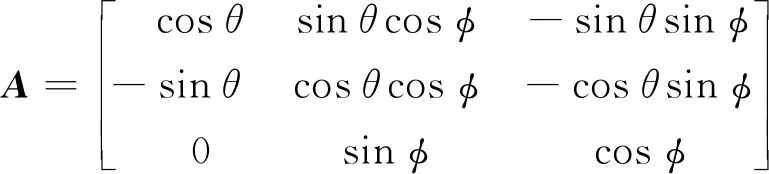
Q为拖体坐标系转换矩阵，

对于位置等参数的转换，需在其基础上加上拖体运动坐标系原点在惯性系下的坐标值.

1.2 拖缆运动控制方程

根据集中质量法思想，将一拖缆从尾端至上端离散为N段，即N+1个节点，其中尾端s=0为第i=0个节点，上端s=S为第i=N个节点.

对第i个节点应用牛顿第二定律，得拖缆节点的基本运动控制方程，即

(3)

Mi=0.5(μi-1/2li-1/2+μi+1/2li+1/2)I+Ma,i

Ma,i=0.5(Ma,i-1/2+Ma,i+1/2)

I为3×3的单位矩阵；μ、l、σ分别为拖缆单位长度的质量、节点间长度、横截面积；下标i+1/2表示节点i和节点i+1间的物理量，如li+1/2表示节点i和节点i+1间的长度，即li+1/2=si+1-si.简便起见，下面将一些公式中的部分下标略去，不再明示.

Fi为作用于节点i上的所有作用力，包括基本的拖缆张力、浮力、重力以及流体阻力，如果拖缆上还有其他的外力也应一并包括进去，

Fi=ΔTi+Bi+Gi+Di

(4)

(1) 张力T.一般情况下缆的应变|ε|≪1，可将应力-应变关系弹性化处理，即

ΔTi=Ti+1/2-Ti-1/2

Ti+1/2=Eσεi+1/2τi+1/2

εi+1/2=

li+1/2-1

其中：τ为缆长方向上的单位切向量；E为弹性模量.同理可得Ti-1/2.考虑到拖缆的拉、压弹性性能不同，本文中拖缆受压(应变为负)时的弹性模量近似取为受拉时的1/10.

(2) 浮力和重力B,G.节点i的浮力和重力可以表示为

Bi+Gi=-0.5ρ(li-1/2σi-1/2+li+1/2σi+1/2)g+

0.5(μi-1/2li-1/2+μi+1/2li+1/2)g

式中：g为重力加速度.

(3) 流体阻力D.将拖缆阻力分为切向和法向分别处理，计入缆应变影响后，可以表示为

Di=0.5(Di+1/2+Di-1/2)

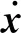
1.3 拖体运动控制方程

借鉴潜艇的运动控制方程[2,11]，水下拖体的6自由度运动控制方程及辅助方程可以表示为

XH+XS+∑Xci

YH+YS+∑Yci

ZH+ZS+∑Zci

MH+MS+∑Mci

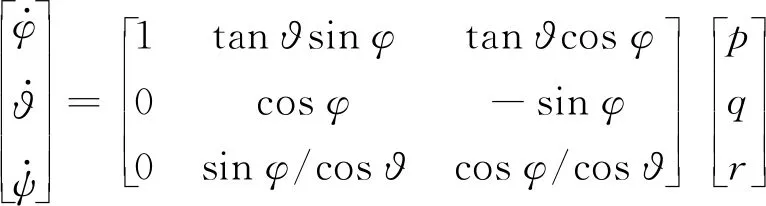
其中：u,v,w为拖体的线速度；p,q,r为角速度；I为各个方向上的转动惯量；拖体的惯性质量记为m；重心、浮心坐标分别记作RG=(xg,0,zg),RB.方程右侧(X,Y,Z,K,M,N)为作用在拖体上的力和力矩，下标H表示拖体水动力，下标S表示拖体重力浮力作用分量，下标c表示拖缆作用力，拖缆作用力将作为边界条件给出.拖体的水动力可忽略高阶小量，表示为

其中：右侧各符号为拖体的水动力导数，具体可参考潜艇操纵性文献.

拖体重浮力作用力分别为

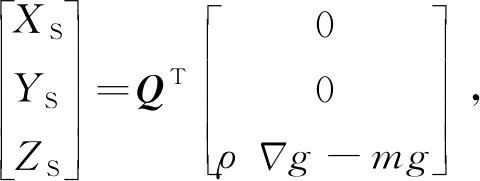
1.4 边界条件

在拖曳系统运动过程中，拖缆与水下拖体/水面拖船是相互作用相互影响的.根据不同的情况，有2种不同的边界条件，拖缆自由端边界条件、水下拖体(水面拖船)-缆耦合条件，下面分别给出，简便起见，在一些公式中将拖缆节点的下标忽略.

(1) 拖缆自由端边界条件.对于没有拖体的自由端(缆B,C)，视其为一节点，直接应用集中质量法控制方程，

(5)

式中：M0=0.5(μ1/2l1/2I+Ma，1/2)；F0=T1/2+0.5(-ρ1/2σ1/2+μ1/2l1/2)g+0.5D1/2.

(6)

式中：(xtb,ytb,ztb)表示拖体在惯性坐标系下的位置；Rtp为拖体坐标系下连接点的坐标值.

而动力耦合边界条件，在拖体/拖船运动坐标系下为：拖缆作用于拖体的作用力(如缆A下端，其余类似)，经坐标转换可表示为

(7)

最终，水面拖船的位置与速度为整个系统的输入，为已知的时间函数；而水下拖体的位置与速度则由拖体的运动控制方程计算得到.

2 数值求解方法

由控制方程，即式(3)可以得到各拖缆(A，B，C)最终的运动控制方程，即

(8)

i=0,1,…,N-1

将上式与拖体运动控制方程和边界条件联立，得到整个系统的运动方程，可采用4阶龙格库塔方法在时域内积分求解.

2.1 拖缆破断的数值实现方法

本文采用较为简单的实现方法：将拖缆破断节点处的E,Ct,Cn等参数置为0，对应的张力和阻力则直接变为0，拖缆即认为从此处破断，而系统的控制方程无需任何变化.

3 数值计算与分析

本文中的拖曳系统由2个阵列缆、1个牵引缆和1个水下拖体组成，其主要参数如表1和2所示，海水密度取为ρ=1 025 kg/m3，无海流，牵引缆上端连接于水面拖曳母船，水面母船的位置与速度为模拟计算的输入量.对整个系统而言，如牵引缆破断，则水下拖体和阵列缆坠海，系统已算全部损毁，该情况没必要考虑，而2个阵列缆同时破断的情况也极难出现，为此作为一般情况，本节计算仅考虑一根阵列缆破断的情况.

各拖缆同拖体连接点坐标分别为A(0, 0, 0)m，B(-1.7, -1.1, 0.0)m，C(-1.7,1.1,0.0)m.拖缆整体上以5 m的间距进行离散，牵引缆离散为24段，阵列缆为40段，节点数量共107个，计算时间步长取为2.0 ms.

表1 各拖缆物理参数 Tab.1 Physical coefficients of the towed cables

表2 水下拖体参数及无因次惯性类水动力导数Tab.2 Coefficients and non-dimensional inertial derivatives of the underwater towed vehicle

图2 系统在不同速度时的稳态解Fig.2 Steady state solutions at different towing speeds

水下拖体一般无大幅机动，其水动力仅保留主要项，这些无因次的水动力导数分别为

3.1 稳态运动计算

作为初始状态，系统以v=4,8,12 kn的速度沿y轴正向运动，水面拖船位置为(0,0,0)m，经长时间计算可得到其稳态运动结果，如图2和表3所示，由于连接点处缆的张力方程不能直接算出， 图中上端张力取为Ti=N-1/2，下端张力为Ti=1/2，如未特别说明下文各图也类似.

表3 拖体的稳态运动参数Tab.3 Steady state variables of the towed vehicle

3.2 破断瞬态响应

为记录拖缆破断时的瞬态响应，数据记录步长取为dt=2.0 ms，其足以记录缆上的冲击响应.计算工况为：v=4,12 kn；破断缆为缆C；破断位置s=50,100,150,200 m.图3及图4给出了不同拖曳速度时，缆上不同参考位置处的张力变化情况，图5为水下拖体的纵向速度变化情况.

结果显示： 缆破断的瞬态响应时长基本在2或3 s以内；拖缆张力变化存在滞后现象(小于0.2 s)，远离破断位置的张力变化的滞后较大， 其中牵引缆上端滞后最大；破断后，牵引缆及破断阵列缆上的张力均降低，而没破断的另一侧阵列缆反倒有些增大；破断缆上张力有较大的振荡冲击现象，可能对阵列中的水听器造成影响或损坏，而其他缆上无冲击现象，仅伴有些高频小幅度的张力抖动；而水下拖体，其速度有快速的升降变化，加速度较大，特别是高速拖曳时.

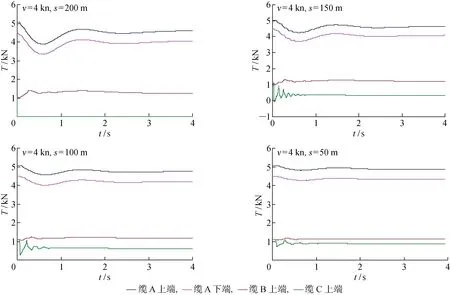
图3 低速运动时破断拖缆瞬态响应Fig.3 Cable instantaneous response of breaking cable at low towing speed

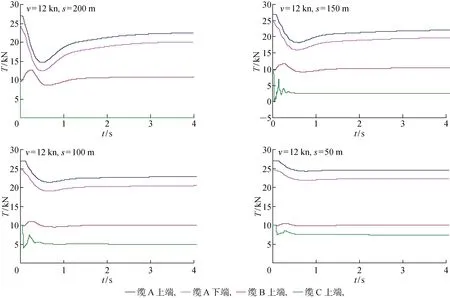
图4 高速运动时破断拖缆瞬态响应Fig.4 Cable instantaneous response of breaking cable at high towing speed

图5 破断时拖体的瞬态响应Fig.5 Instantaneous response of towed body when cable breaks

3.3 破断后长期响应

计算工况同上一节一样，数据记录步长取为0.5 s，本节给出系统从破断开始到达到稳定后(取为500 s)的长期运动响应，分别如图6，表4所示.

表4 破断后拖体的稳态运动参数

Tab.4 Steady state variables of the towed body after breaking

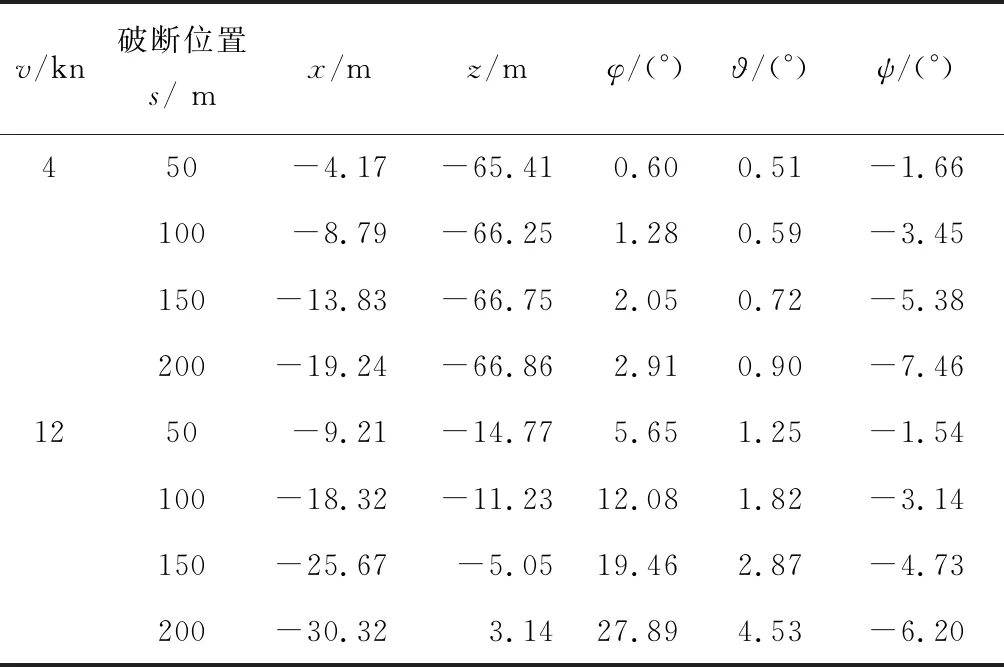
v/kn破断位置s/ mx/mz/mφ/(°)ϑ/(°)ψ/(°)4 50-4.17-65.410.600.51-1.66100-8.79-66.251.280.59-3.45150-13.83-66.752.050.72-5.38200-19.24-66.862.910.90-7.461250-9.21-14.775.651.25-1.54100-18.32-11.2312.081.82-3.14150-25.67-5.0519.462.87-4.73200-30.323.1427.894.53-6.20

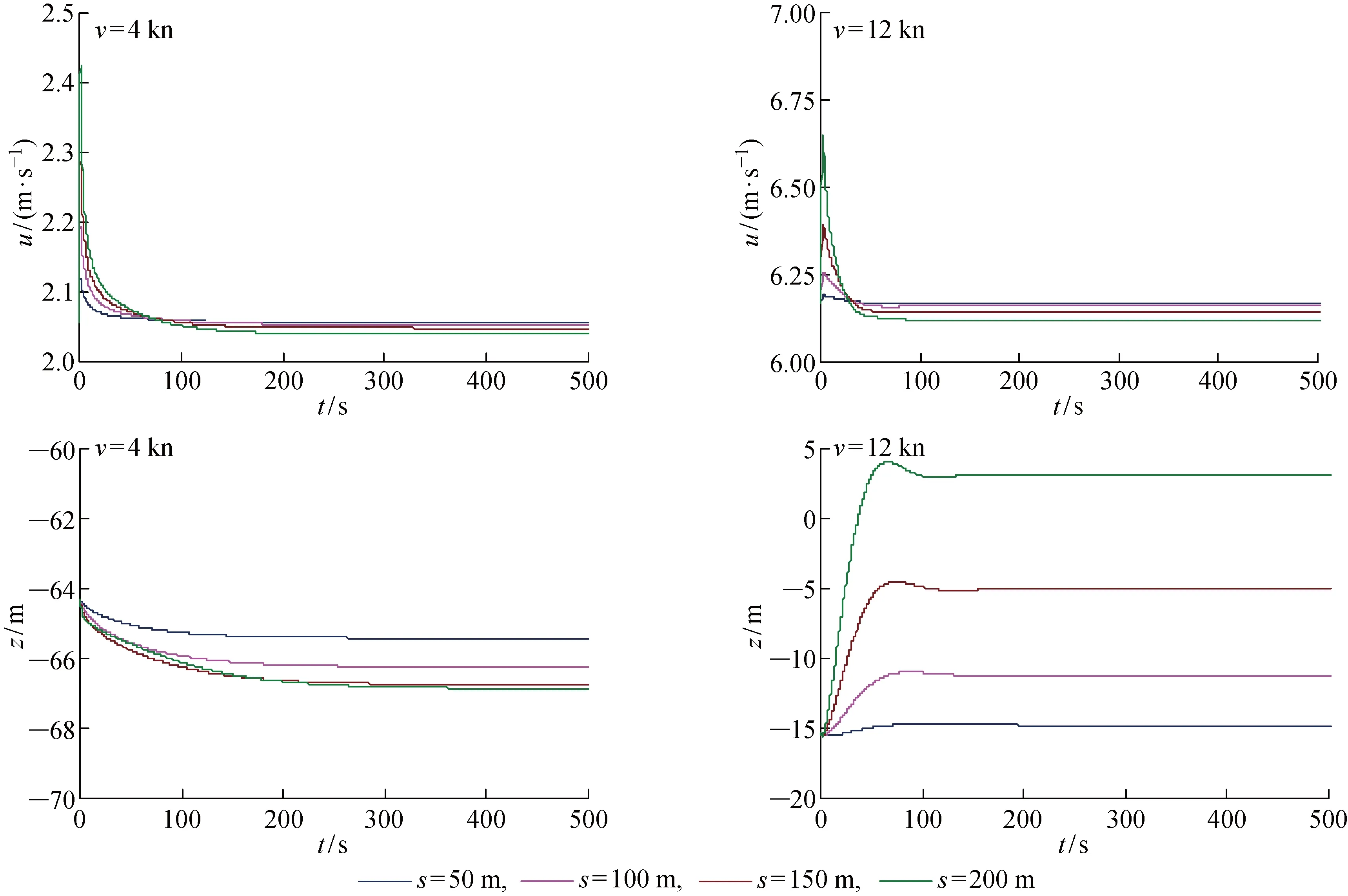
图6 破断后拖体的运动响应Fig.6 Response of towed body after breaking

由结果可以看出：不论破断缆长度如何，系统长期响应变化较平稳，无太大的冲击现象，破断后100 s左右系统基本重新达到稳定状态，侧向位置偏向破断缆的另一侧；低速运动时缆破断后其在水下的深度稍有增加(z值减小)，但高速运动时其在水下的深度大幅减小，甚至跳出水面 (v=12 kn， 破断位置s=200 m时)，该情况将导致整个系统的损毁；对于水下拖体而言，破断后横倾角、纵倾角及艏向角均会发生不同程度的变化，低速时或破断缆长度较小时，角度变化不大，系统还可以继续工作，但高速时横倾角变化很大，基本超出正常的工作范围.

3.4 系统回转中破断响应

系统速度为v=8 kn，回转半径R=100 m，右侧回转，在回转过程中t=76 s时(回转至半圈)缆破断，破断位置s=100 m；本节考虑回转外侧阵列缆B和内侧阵列缆C破断两种情况.图7给出了破断时缆的瞬态张力变化，可见回转时破断的瞬态响应特性同直航时的类似；但外侧阵列破断时牵引缆上张力有些降低，而内侧缆破断时张力起初降低而后回复.图8和9给出了破断后缆的张力变化及水下拖体的位置变化情况，作为对比给出了没有破断时的情况，如图中实线所示；而系统在整个过程中的空间阵形曲线由图10给出，其中虚线是没破断时系统的空间阵形，2根阵列缆近似平行错开，无交叉碰撞现象.

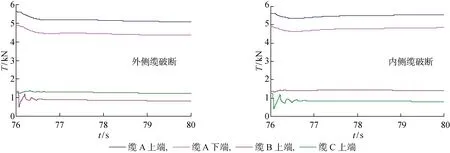
图7 破断时缆的瞬态张力变化Fig.7 Instantaneous response of cable tension when cable breaks

图8 破断后缆的张力变化Fig.8 Response of cable tension after breaking

图9 破断后水下拖体深度变化Fig.9 Depth history of towed body after breaking

图10 破断后系统空间阵形(俯视图)Fig.10 Spatial configurations of cables after cable breaking (horizontal view)

由计算结果可以看出，同未破断时的响应相比，外侧缆破断时牵引缆张力有较明显的降低，而内侧缆破断时牵引缆张力仅有小幅的跳动，变化不明显，回转结束后其逐渐趋于稳态值；水下拖体在水下的深度，外侧缆破断时有小幅增大(z值减小)，内侧缆破断时稍有减小，回转结束后其逐渐趋于稳态值，均小幅减小.图9显示，回转中缆破断后，破断缆均向回转圈外侧偏移，外侧缆破断后两个阵列缆错开的间距增大不会发生碰撞缠绕现象，但内侧缆破断后外偏同另一阵列有水平面交叉，在实际海洋环境中很有可能发生碰撞缠绕现象，致系统损坏.

4 结语

本文针对水下双阵列拖曳系统，采用数值方法详细研究了阵列缆破断时系统的瞬态运动响应及后期的运动响应.文中基于集中质量法建立了拖缆的运动模型，而拖体采用潜艇的6自由度运动模型，通过建立缆-拖体耦合边界条件将其耦合成一个整体，采用龙格库塔方法进行积分求解，同时给出了拖缆破断的数值处理方法.最后展开数值模拟计算，详细探讨了系统在不同破断情况下的运动响应特性.计算结果表明：

(1) 破断瞬态响应时长基本在2或3 s以内，拖缆张力变化存在滞后现象，破断缆上张力有较大的振荡冲击现象，而其他缆张力变化较平稳，同时水下拖体速度有快速的升降变化；

(2) 系统破断的后期响应变化较平稳，拖体在水下的深度低速时增加，高速时减小，甚至跳出水面；

(3) 回转机动中，外侧缆破断时牵引缆张力有较明显的降低，拖体在水下的深度也有小幅增加，而内侧缆破断时牵引缆张力变化不明显，拖体的水下深度有小幅减小，不论内侧还是外侧缆破断后均向回转圈外侧偏移，以致内侧缆破断后同另一阵列在水平面上交叉，可能发生碰撞缠绕现象.