双圆弧谐波传动齿廓参数对柔轮应力影响
2020-03-09蒋倩倩王家序李俊阳
蒋倩倩, 王家序,2, 李俊阳, 肖 科, 唐 挺, 王 成
(1. 重庆大学 机械传动国家重点实验室, 重庆 400044; 2. 四川大学 空天科学与工程学院, 成都 610065)
谐波齿轮传动依靠柔轮的波动变形原理传递运动与动力,柔轮疲劳断裂失效是谐波齿轮传动装置最主要的失效形式[1].因此,准确地分析柔轮应力和变形规律是谐波齿轮传动的研究重点.
目前,研究柔轮应力与变形的方法主要有实验归纳法[2]、理论公式法[3]和有限元法(FEM)[4-5].实验法直观准确,但受成本、周期等客观条件的限制,且无法获取柔轮内部的应力应变情况.柔轮应力理论计算模型是建立在柱壳模型上,基于Kirchhoff-Love等假定与简化来推导理论公式,并根据实验结果加入修正系数[3].但理论模型未考虑装入刚轮后产生的预紧力及其引起的应力增大.预紧力的存在,约束了柔轮变形,使得柔轮与刚轮的啮合侧隙和齿间载荷分布状态发生变化,柔轮应力也随之改变.随着计算机技术的提高,FEM被广泛用于研究谐波齿轮传动的应力应变.为节约计算时间,研究者大多采用等厚齿圈有限元模型代替轮齿,以优化柔轮的几何结构参数,近几年的研究侧重于齿间载荷分布和柔轮的变形函数.Dong等[6]采用APDL语言建立了波发生器装配的有限元动力学模型,分析柔轮的动态应力和载荷分布,拟合柔轮变形函数.Routh等[7]利用有限元法模拟刚轮与渐开线柔轮在传动过程中的齿间啮合载荷分布规律.Sahoo 等[8-9]通过FEM估算在空载下渐开线柔轮的筒体应力、应变和初始转矩,确定齿间啮合载荷分布情况,并采用实验法予以验证.陈晓霞等[10]以三维弹性接触有限元模型计算渐开线不同线层的应力分布情况.以上研究分析了空载和负载下刚轮与柔轮的齿间载荷和应力应变分布状态.然而,柔轮的齿根应力与柔轮齿廓参数关系密切,目前几乎没有文献涉及柔轮齿廓参数对柔轮应力的影响规律.
基于此,本文以无公切线式双圆弧谐波齿轮为研究对象,采用包络理论设计共轭刚轮齿廓,通过在Abaqus中建立完整的谐波齿轮三维弹性接触有限元模型,将柔轮的装配状态分为波发生器装配、刚轮装配以及加载3个分析步,结合响应面模型分析柔轮齿廓参数对每个分析步的柔轮变形与应力的影响规律,以期优化柔轮齿廓参数、降低柔轮应力、提高柔轮疲劳强度,为建立柔轮的疲劳强度评价准则提供依据.
1 双圆弧谐波齿轮传动共轭齿廓设计
1.1 无公切线双圆弧齿廓
谐波齿轮传动中,圆弧齿廓分为单圆弧齿廓和公切线双圆弧齿廓,目前的齿廓研究侧重于后者.考虑到公切线式双圆弧齿廓的切线高系数(切线与凸齿廓切点到柔轮齿顶的高度系数)为0时,刚轮与柔轮的包络存在区间较大[11],为获得较大的“双共轭”啮合区间,本文提出改进的无公切线双圆弧齿廓,以柔轮轮齿对称线为Y1轴,Y1轴与中面曲线交点为原点O1,过原点O1作中面的切线为X1轴,建立柔轮齿局部坐标系O1X1Y1,如图1所示.图中各参数的意义如表1所示.
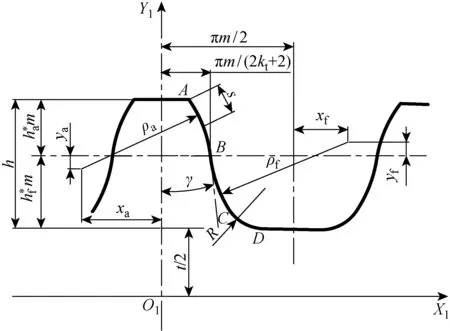
图1 双圆弧齿廓示意图Fig.1 Schematic diagram of double arc tooth profile
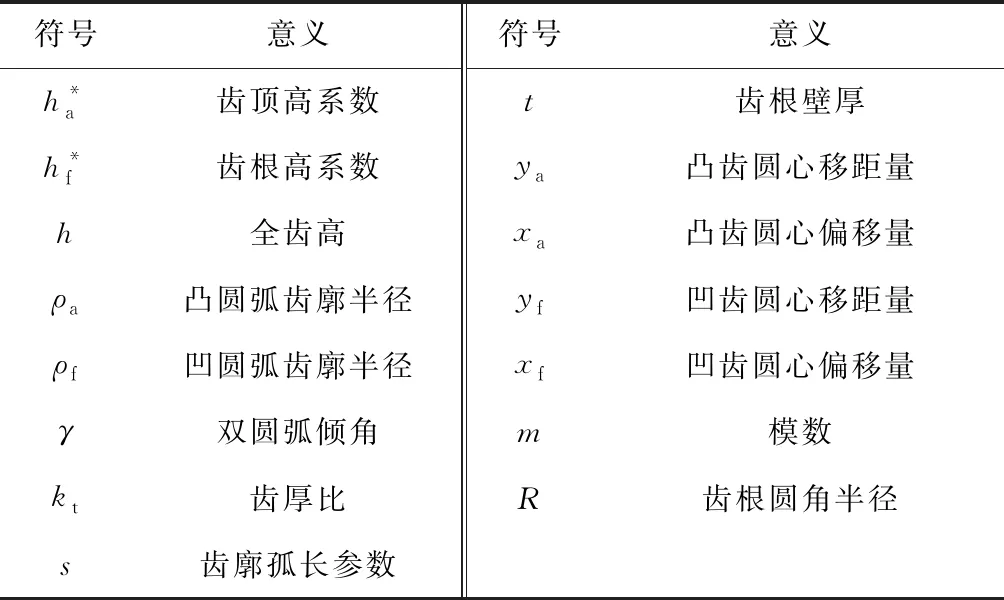
表1 齿廓参数意义Tab.1 Means of parameters of tooth profile
无公切线双圆弧齿廓由凸圆弧AB、凹圆弧BC与齿根过渡圆弧CD组成.其中:圆弧AB与圆弧BC相切于点B;切点B与柔轮的分度圆重合;圆弧CD分别与圆弧BC和柔轮的齿根圆相切.用分段函数表示AC段圆弧齿廓[11].
AB段凸圆弧齿廓为
(1)
式中:s∈(0,l1),l1为AB段齿廓弧长,l1=ρa(αa-γ);αa为AB段齿廓齿顶压力角,αa=arcsin[(ha+ya)/ρa];xo a=-xa;yo a=hf+t/2-ya.
BC段凹圆弧齿廓为
(2)
式中:s∈(l1,l2),l2为BC段齿廓弧长,l2=l1+ρf(αf-γ);αf为BC段齿根压力角,αf=arcsin[(hf+yf)/ρf];xof=πm/2+xf;yof=h-ha+t/2+yf.
1.2 基于包络法的刚轮共轭齿廓设计
在椭圆波发生器作用下,柔轮的径向变形量(w)、切向变形量(v)以及变形倾角(μ)分别为
(3)
式中:a和b分别为变形后柔轮中线长轴半径和短轴半径,a=rm+w0,b=rm-w0,rm为未变形时柔轮的中线半径,w0为柔轮最大径向变形量;φ为柔轮输出端相对于波发生器长轴的转角;ρ为当装入波发生器时,柔轮变形后的中线矢径.
以刚轮的中心为圆心O2,以刚轮的齿槽对称轴为Y2轴,从圆心O2出发,作X2轴垂直于Y2轴,建立刚轮坐标系O2X2Y2,根据谐波齿轮传动的坐标转换和摩擦模型运动学理论[2],得到在坐标系O2X2Y2中,刚轮齿廓坐标为
(4)
式中:x2和y2分别为刚轮的右侧齿廓在坐标系O2X2Y2中的坐标值;Φ为柔轮轮齿对称轴与刚轮齿槽对称轴的夹角,Φ=μ+Δφ,Δφ为柔轮中线矢径ρ与Y2轴的夹角.
利用包络理论求解与柔轮齿廓坐标共轭的刚轮齿廓坐标,需满足共轭方程
(5)
采用数值离散思想,把每段圆弧的弧长参数s离散为n个点,将式(1)~(4)代入式(5)分段求解出不同s对应的转角φi(i=1,2,…,n),φi的集合称为共轭区间,其对应的坐标点集合为共轭齿廓.以两段相切的圆弧拟合共轭齿廓上一系列离散的数值点,以最小二乘法将数值离散点拟合为圆弧曲线,即可得到刚轮齿廓.
2 双圆弧谐波齿轮有限元分析
2.1 共轭空间齿廓计算实例
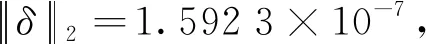
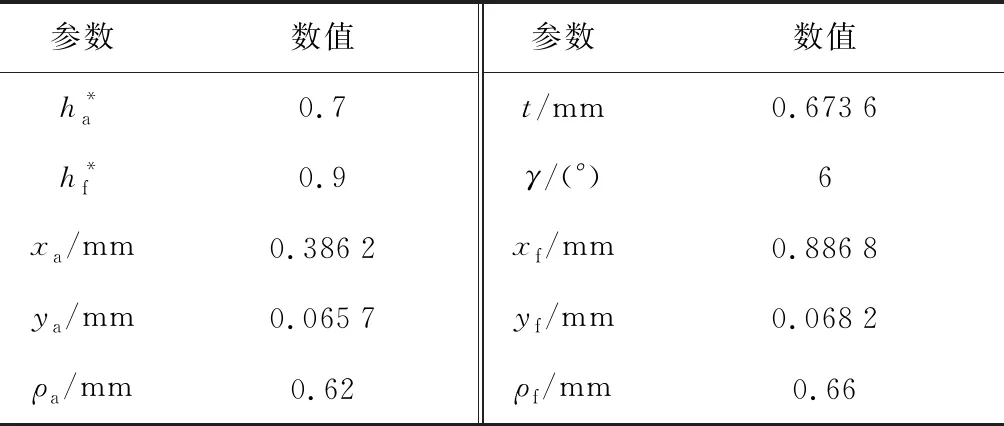
表2 柔轮齿廓参数Tab.2 Flexspline tooth profile parameters
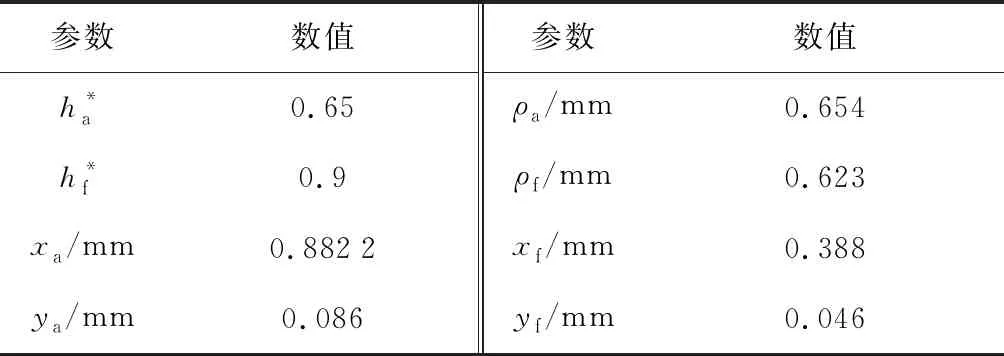
表3 刚轮齿廓参数Tab.3 Circular spline tooth profile parameters
图2所示为柔轮轴向齿廓,以图中所示垂直于柔轮轴向母线的截面为主截面,图中α、β分别为柔轮轴向前端、后端修形角度.由于柔轮在波发生器作用下轮齿产生变形和法向倾角,柔轮和刚轮齿在主截面完全啮合,但柔轮轴向的其他截面均存在不同程度的齿廓啮合干涉.为消除齿廓干涉,且不改变每个截面的齿廓形状,设计柔轮轴向齿形为梯形,分L1、L2和L33段,L1=2.47 mm,L2=3.2 mm,L3=5.23 mm,通过调整柔轮L1和L3段的齿根壁厚,降低柔轮齿廓截面的位置,从而实现齿廓无干涉啮合.
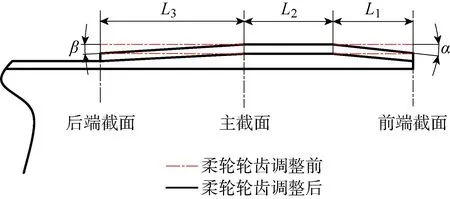
图2 柔轮轴向轮齿修形示意图Fig.2 Diagram of flexspline axial gear modification
柔轮齿根壁厚的调整量是基于包络法及谐波传动坐标转换关系选取的,具体方法为采用MATLAB参数化编程.观察柔轮单个轮齿相对于刚轮齿槽的运动轨迹图,通过调整柔轮前端和后端截面的壁厚,使得柔轮前端与后端截面均处于刚轮齿槽内部,再根据柔轮壁厚调整量与齿宽的线性关系,确定其余各截面的壁厚调整量.
由MATLAB仿真分析求得当前端截面与后端截面的壁厚调整量分别为0.14 mm和0.072 mm时,α=1.414°,β=0.789°,在刚轮的坐标系O2X2Y2中,柔轮轮齿相对于刚轮齿槽的运动轨迹如图3所示.由图3可知,在调整轮齿齿根壁厚后,柔轮前端截面、主截面与后端截面均能实现齿廓无干涉啮合.

图3 柔轮各截面的运动轨迹Fig.3 Trajectory of each flexspline section
2.2 仿真实体建模
建立谐波减速器三维模型,利用ANSYS划分网格,采用八结点六面体单元C3D8R,测试柔轮应力对网格数量的依赖性.发现随着网格数量的增加,柔轮应力不断增大.固定刚轮网格数量为105个,柔轮网格平均每增大104个,柔轮应力增大130 MPa左右,当总体网格数量增加至4×105个时,柔轮应力趋于稳定.考虑柔轮结构变形特点,由于波发生器与柔轮内壁、柔轮与刚轮轮齿接触状态和区域未知,设置“面—面”接触对,摩擦因数取0.15,柔轮为接触面,刚轮内壁、波发生器外表面为目标面,保证三者间初始装配状态无干涉.Augmented Lagrange 乘子法结合了Lagrange乘子法和罚函数的优点,两者形成互补作用,采用该方法在不增加系统自由度的基础上,提升了方程矩阵的对角优势,改善了收敛性.
材料的性能参数如表4所示,柔轮材料为30CrMnSiA,刚轮和波发生器材料为45#优质碳素结构钢.
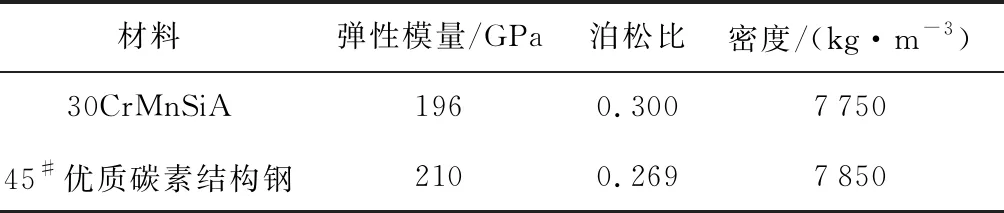
表4 材料性能参数Tab.4 Material performance parameters
谐波齿轮装配状态分为3步,如图4所示.图中观测点位于柔轮主截面长轴右侧第1个轮齿的齿根处,距柔轮筒底的距离为24.23 mm,与柔轮长轴夹角约为2°.记每个分析步观测点处的柔轮应力为σi,i=1,2,3.分析步分别为:① 建立一个与柔轮筒底圆孔固结的参考点,并添加固定约束.波发生器设置位移约束,椭圆形波发生器装配后,在长轴方向使柔轮筒体张开角度α;② 刚轮设置位移约束,从后端装入柔轮,张角被刚轮压下;③ 释放柔轮绕轴向的旋转约束,在柔轮输出端施加额定转矩T,T=63 N·m.由于柔轮的应力求解为非线性大变形问题,求解选项开启“大变形”设置.为提高求解收敛性,最小求解增量步调整为10-9.
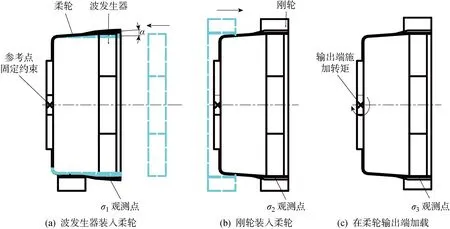
图4 谐波齿轮有限元模型分析步示意图Fig.4 Diagram of harmonic gear finite element model analysis step
2.3 柔轮应力影响因素分析
采用Abaqus进行谐波减速器的三维弹性接触有限元分析,3个分析步的柔轮齿圈应力(σ)云图如图5所示.观测处柔轮圆周方向的变形量对比结果见图6,图中:w0为理论值;w1、w2及w3分别表示装入波发生器、装入刚轮与加载后,柔轮圆周方向中线的径向变形量;v1、v2及v3分别表示装入波发生器、装入刚轮与加载后,柔轮圆周方向中线的切向变形量;v0为理论值.
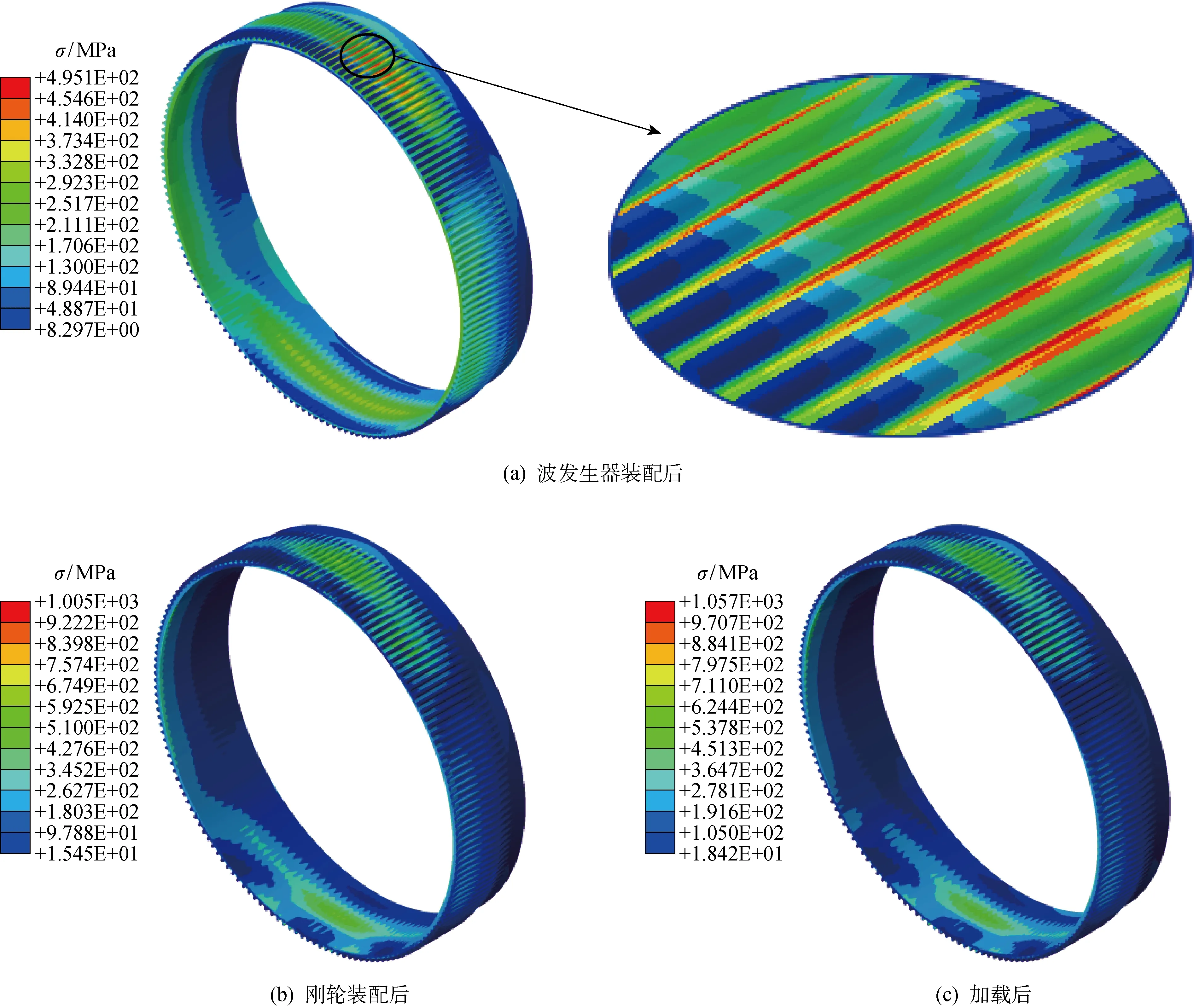
图5 柔轮齿圈的应力云图Fig.5 Stress cloud of the flexspline ring gear

图6 柔轮径向与切向变形量理论值与FEM值对比图Fig.6 Comparison of theoretical and FEM values of radial and tangential deformation of the flexspline
由图5(a)可知,椭圆形波发生器装配后使柔轮产生变形,且最大应力出现在长轴附近的齿根位置.对比图5(a)和5(b),发现刚轮装配后柔轮的最大应力由495.1 MPa增大到 1 000.5 MPa,结合图6中w1与w2及v1与v2的对比,可知刚轮与柔轮之间的啮合齿对会约束装入波发生器时产生的柔轮变形,从而影响柔轮的应力值.
对比图5(b)和5(c),发现加载后柔轮的最大应力仅增大4%左右,且图6中w2与w3及v2与v3均几乎重合,说明谐波齿轮传动是多齿啮合传动,额定载荷均匀分布到单个齿对时,载荷对柔轮应力与变形作用较小.
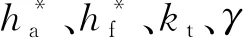
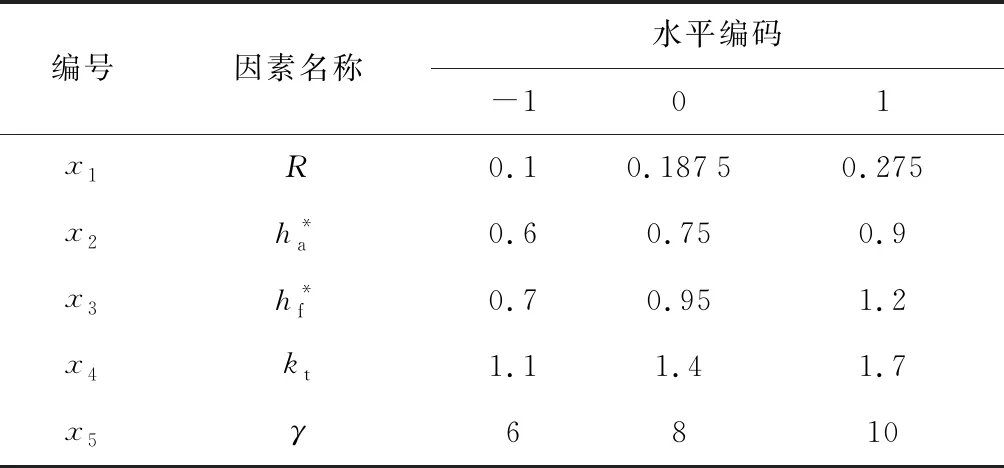
表5 因素范围与水平表Tab.5 Factors range and level table
3 基于响应面模型的柔轮应力规律分析
3.1 响应面模型建立
为了提高拟合精度,采用响应面法设计5因素5水平的实验方案,单个因素的水平编码值分别为 -1,0,1,共26组仿真实验.额定载荷对柔轮应力与变形的影响不明显,因此仿真仅采集波发生器作用下的柔轮压力σ1和刚轮作用下的柔轮应力σ2.
根据实验结果采用最小二乘法对仿真结果拟合,所得σ1和σ2的影响面模型分别为
(6)
分别对两个响应面模型做回归显著性检验,当响应面模型的不显著水平(P>F)小于0.05时,表示拟合的响应面模型是有效的,其值分别为 0.000 1 和 0.011 7,说明模型非常重要,在σ1的模型中x1、x2、x3和x4是模型的重要因素,在σ2的模型中x2、x4、x5和x52是模型的重要因素.
各因素的一次项对模型响应的敏感度如图7所示,由σ1的模型可知,x3和x5与σ1呈正相关,其余因素与σ1呈负相关.对比σ2的模型中各因素系数的绝对值,一次项系数显示各因素对该模型的影响程度为x4>x2>x5>x1>x3,二次项系数显示各因素的影响程度为x5>x1>x3>x2>x4.综合分析可知,x4、x5对模型σ2影响最大,x2、x1次之,x3的影响最小,即在刚轮作用下,齿厚比和双圆弧倾角对柔轮应力影响最大,齿顶高系数、齿根过渡圆角半径次之,齿根高系数影响最小.对比模型σ1和σ2各因素的系数项可知,x1、x2、x3、x4和x5对σ1的敏感度小于对σ2的敏感度,即柔轮齿廓参数对仅有波发生器作用下的柔轮应力影响较小,但在刚轮装配后,由波发生器撑开的柔轮筒体张角被压下,导致刚轮与柔轮齿间接触力增大,迫使柔轮的变形和齿间侧隙发生改变,柔轮齿圈应力升高,因而柔轮应力对齿廓参数变化的敏感度也随之提高.因此,要建立合理的柔轮疲劳寿命评价体系需要准确分析柔轮齿廓单因素对柔轮应力影响规律.
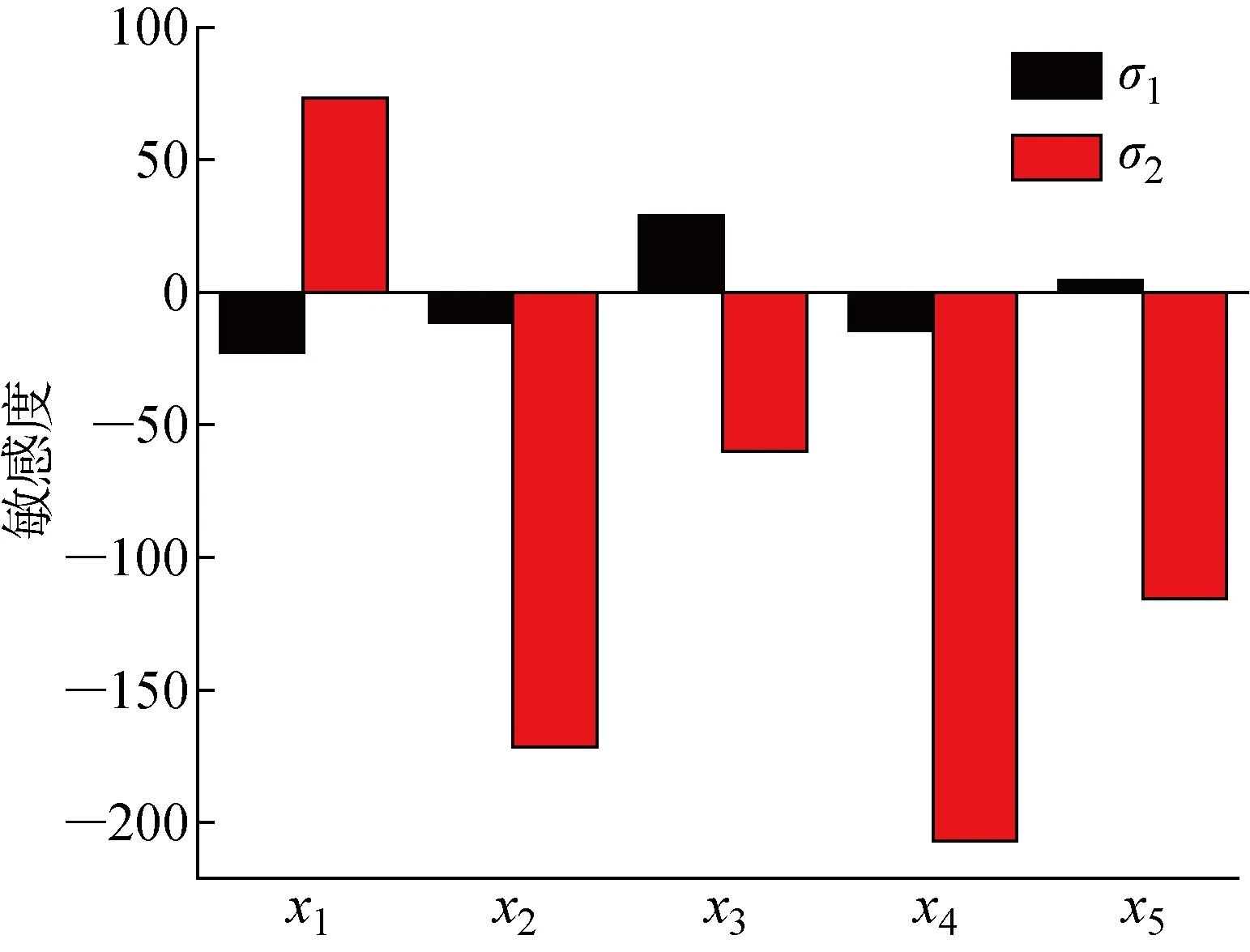
图7 各因素对不同模型柔轮应力的敏感度分析Fig.7 Sensitivity analysis of various factors on flexural stress in different models
3.2 柔轮齿廓参数对柔轮应力的影响规律分析
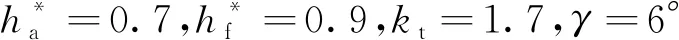
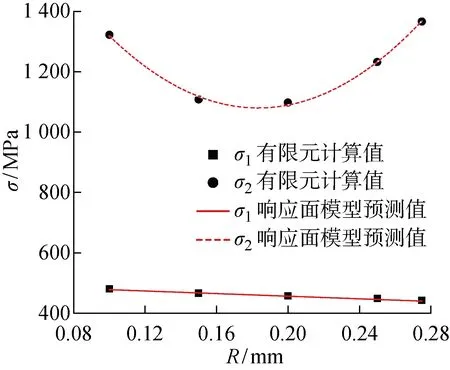
图8 柔轮齿根圆角半径对柔轮应力的影响Fig.8 Effect of flexspline root radius on flexspline stress
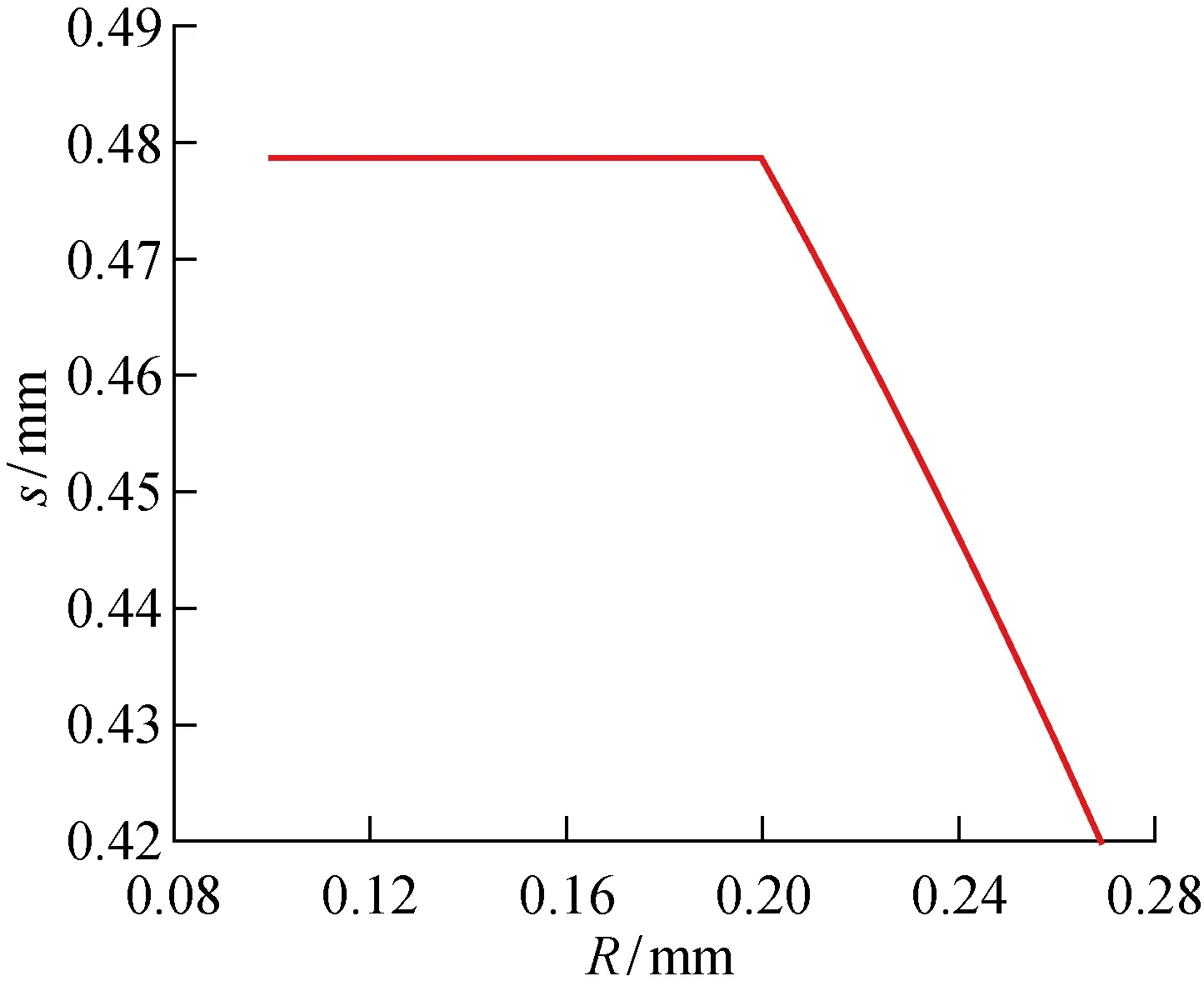
图9 柔轮齿根圆角半径对工作齿廓弧长的影响Fig.9 Effect of flexspline root radius on working arc length
从图中可以看出,随着R的增大,σ1单调递减;σ2呈先减小后增大的抛物线变化趋势,其原因见图9.当R增大时,柔轮凹齿廓弧长减小,刚轮和柔轮的工作齿廓弧长从保持不变到逐渐变短,从而导致柔轮齿根应力有所上升.因此在无齿廓干涉和工作齿廓弧长保持不变的前提下,增大齿根过渡圆角半径有利于减小柔轮应力.
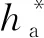

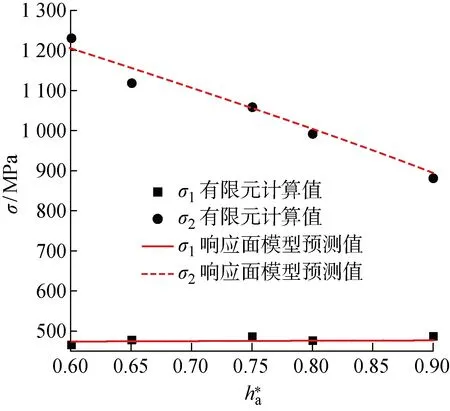
图10 柔轮齿顶高系数对柔轮应力的影响Fig.10 Effect of flexspline tooth top coefficient on flexspline stress
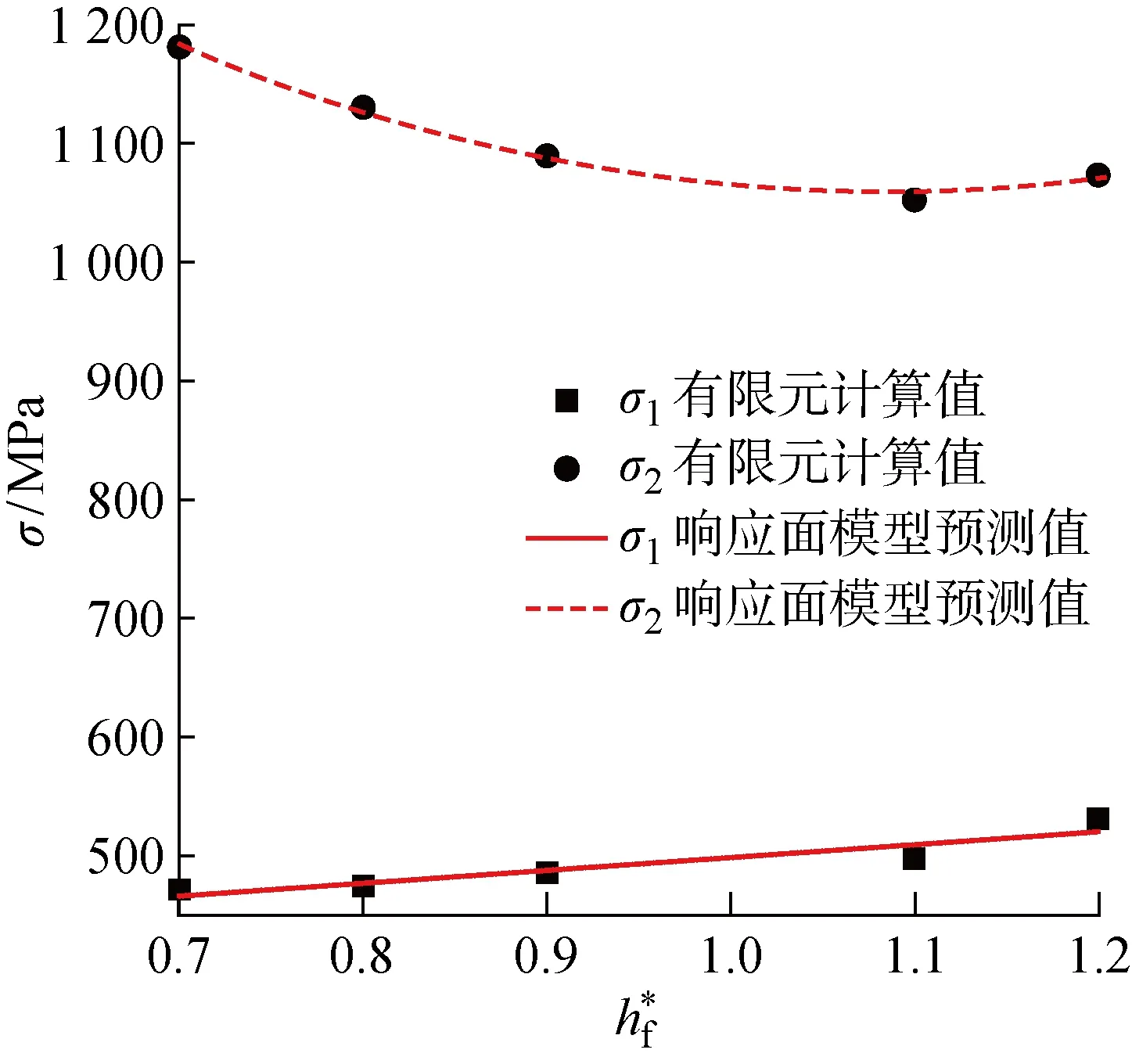
图11 柔轮齿根高系数对柔轮应力的影响Fig.11 Effect of flexspline root height coefficient on flexspline stress
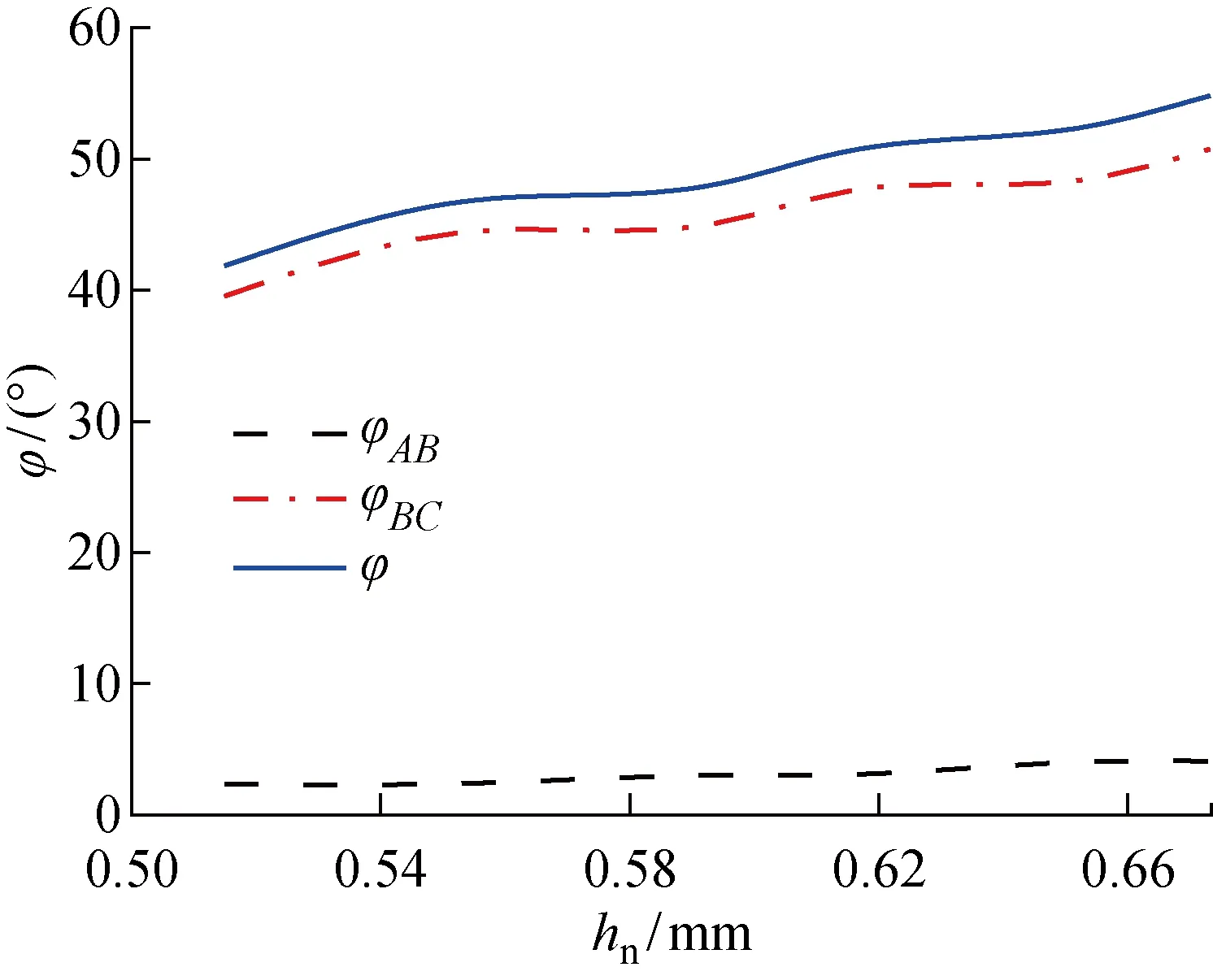
图12 最大啮合深度对共轭区间的影响Fig.12 Effect of maximal engagement depth on conjugate interval
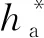
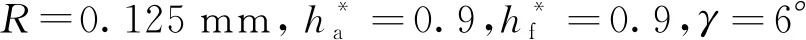
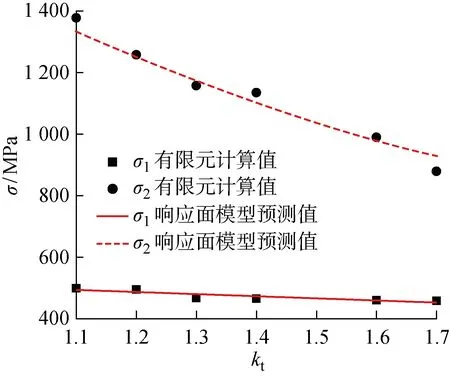
图13 柔轮齿厚比对柔轮应力的影响Fig.13 Effect of flexspline tooth thickness ratio on flexspline stress
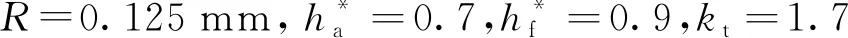
随着γ的增大,σ1没有明显的变化,σ2则呈单调递减趋势.这是由于当双圆弧倾角增大时,与柔轮共轭的刚轮凸齿廓半径增大,凹齿廓半径减小,柔轮齿根弯曲强度提高,承载能力增大,所以在工艺条件允许的情况下,双圆弧倾角取较大值为优.
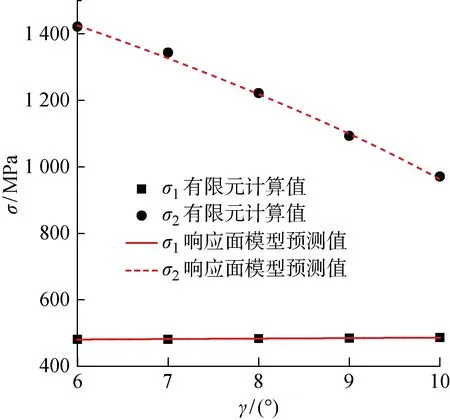
图14 柔轮双圆弧倾角对柔轮应力的影响Fig.14 Effect of flexspline double-circular-arc on flexure stress
4 结论
(1) 刚轮装配后,刚轮与柔轮之间的啮合齿对及啮合情况将对柔轮的变形产生约束,从而对柔轮的变形应力产生显著影响.因此,圆弧齿廓谐波传动的齿形参数是计算柔轮疲劳寿命时不可忽略的因素之一.
(2) 由于谐波齿轮传动是多齿啮合传动,且啮合区间较大,当载荷分布到多个接触齿对时,每个齿对承受的载荷较小,所以载荷对柔轮变形和应力影响较小.
(3) 齿厚比和双圆弧倾角对柔轮应力影响最大,齿顶高系数、齿根过渡圆角半径次之,齿根高系数影响最小;在不影响齿廓工作弧长的条件下,增大柔轮齿根过渡圆角半径有利于减小柔轮变形应力;齿根高系数不大于1.1 mm,且增大齿顶高系数、齿厚比与双圆弧倾角有利于减小柔轮变形应力.
