地下管线在地表爆炸荷载下的位移响应与参数分析

王亚光， 廖晨聪， 张 琪

(上海交通大学 土木工程系； 海洋工程国家重点实验室， 上海 200240)

随着我国城市规模的不断扩张，地下管线作为城市生活功能的主要设施在全国范围内大量铺设.此外，我国大型暗埋管道工程如南水北调以及西气东输等工程中，地下管道承担着运输石油、天然气以及水资源等的重要作用.然而，目前大部分管道暗埋深度较浅、地理跨度较大，所处环境复杂.管道周边地面爆炸，比如汽车炸弹、战争爆炸以及意外爆炸都可能对既有管线造成不同程度的破坏.一旦管道发生破坏，管线内运输资源的泄漏就会带来巨大经济损失及环境问题.因此，对既有管线进行爆炸荷载下动态响应的评估尤为重要.

在以往的地下顶管设计中，往往仅考虑管道内部荷载、穿越地质条件以及埋设方式等因素，较少评估地面爆炸等高度非线性荷载的影响[1].刘建民等[2]通过数值计算分析了埋地管道在浅埋爆炸和地面爆炸荷载下的动态响应.梁政等[3]和Yang等[4]应用LS-DYNA软件分析了地下隧道在地表爆炸荷载下的结构响应，分别讨论了药量、管道壁厚等参数以及结构脆弱区范围的问题.Wang等[5]通过SPH与FEM方法的联合应用分析了地下结构物在浅埋爆炸荷载下的动态响应.Jiang等[6]研究了地表爆炸对既有地下结构的环境影响，建立了隧道单元和围岩单元之间相对速度和有效拉应力的关系.Shin等[7]以隧道振动为主要观测指标分析了侧向爆炸对于岩石中隧道的影响.但是上述研究中均忽略了土中孔隙水的作用.Yu等[8-9]对隧道在爆炸荷载下的响应做了深入研究，侧重分析了爆炸导致的振动对结构带来的影响.Kouretzis等[10]在忽略了土-结相互作用基础上，推导出柔性管线分别在P波和瑞利波作用下的管线应变,但该解析解简化条件过多，应用有限.Feldgun等[11]基于耦合Godunov变分法，计算了土体-管线接触应力，分析了饱和多孔介质中管线在侧向爆炸荷载作用下的动态响应，其中孔压分析是通过本构内嵌经验公式所得，并没有考虑水土相互作用.De等[12-13]通过离心机模型试验以及数值模型分析了地面爆炸对于地下结构物的影响,研究了干砂中地下隧道维护材料的结构保护效果.Liao等[14]分析了动力荷载下的孔压和液化，但荷载相比于爆炸工况则没有很强的参考价值.Li等[15-16]利用数值方法分析了低非线性荷载对于地下结构物的影响.

由此可见，既有研究主要侧重于爆炸振动对结构造成的影响，但忽略了土中孔隙水的作用.然而在我国东部沿海地区，钢顶管等地下结构大多位于地下水位之下，孔隙水会对饱和土在动荷载下的响应产生不可忽视的影响[17]，忽略孔隙水压力会使得计算结果产生一定偏差.因此，本文在前述研究基础上，将u-p模型嵌入有限元程序，分析地下顶管在地面爆炸荷载作用下的响应，以结构位移为观测对象，对炸药当量、起爆位置、钢顶管上覆土厚度、管径等进行参数分析，以期对地下工程结构的设计施工提供有益的参考.

1 数值计算模型

1.1 高爆材料及理想气体本构

地面爆炸荷载采用的是High_Explosive_Burn高爆材料模型和Jones-Wilkins-Lee(JWL)状态方程模拟爆炸产物与比体积的关系.JWL状态方程的表达式如下[18]：

(1)

式中：pt为爆炸产物的压力；e为炸药的内能；v为比体积；C1,C2,r1,r2,ω均为实验确定的材料参数.本文中的炸药采用TNT，参数如表1所示.表中：ρ为炸药密度；vD为爆炸速度；pCJ为爆轰波阵面压力；E0为单位体积炸药内能；V为气体体积.长方体炸药位于地表，平面尺寸为1 m×1 m,通过改变炸药材料高度模拟不同爆炸当量.

表1 TNT材料参数Tab.1 Material parameters of TNT

采用NULL空材料和线性多项式状态方程描述爆炸作用下的空气，其状态方程如下：

pair=(0.4+0.4μ2)Eair

(2)

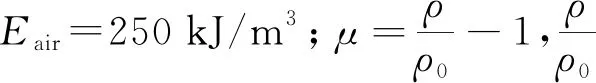
1.2 多孔介质本构方程和钢顶管材料本构

多孔介质饱和度对于土体的动力响应影响显著[19]，因此选取合适的土体本构模型对于计算精度与可靠性非常关键.本文选用了基于摩尔库伦破坏准则的Federal Highway Administration (FHWA)模型[18]，该模型可以考虑土体的应变速率、应变软化、随动强化等特性，通过嵌入孔隙水压力与有效塑性体积应变的经验公式考虑孔压特性.本文所得孔隙水压力则是通过将u-p模型嵌入有限元程序，计算过程在下一小节中详细描述.

研究表明，爆炸波的衰减速率随着土体饱和度的上升而下降[20]，即饱和土中的地下结构相比非饱和土中的结构在爆炸荷载的作用下更加危险.考虑到大多数钢顶管处于地下水位以下，同时为了计算模型的简化，将土体模型视为完全饱和土.本文中选用的土体参数模拟长江三角洲地区的土体特性[21]，另外选择理想弹塑性本构模拟钢顶管在爆炸荷载下的响应，参数设置如表2所示.

表2 土体和钢顶管参数Tab.2 Paremeters of soil and pipe jacking

1.3 u-p模型

土体是由土骨架，空气以及孔隙水组成的多相介质，饱和土的动力学性质是由土骨架和孔隙水的相互作用决定的[17].考虑到土体在爆炸荷载作用下，孔隙水压力的改变会影响土体强度，采用土骨架和孔隙水视为分别运动又相互作用的耦合方法更为适合.依据Biot流固耦合理论，土体介质由动量守恒方程、能量守恒方程以及质量守恒方程共同控制.

(3)

(4)

(5)

式中：M为全局质量矩阵；C为黏性阻尼矩阵；K为刚度矩阵；Q为耦合矩阵；G为动态渗流力矩阵；S为流体压缩矩阵；H为渗透系数矩阵；U和P分别代表位移和孔隙水压力向量；FP和FU分别为节点力和节点流量.

2 模型验证

选取实验数据[20]对数值模型进行验证.验证模型如图1所示，炸药埋置于地表以下2.5 m处，应力监测点水平分布于地表以下2.5 m处.在炸药周围2 m范围内，爆炸会造成巨额能量的瞬间释放，使得爆炸点毗邻区域产生巨大变形，如果采用传统的Lagrange算法，网格畸变后则会造成计算不收敛.所以在验证模型中，距离炸药附近2 m×6 m范围内采用ALE算法处理爆炸引起的土体大变形问题，局部单元网格尺寸为20 cm，远端土体模型采用Lagrange算法.模型左侧为对称边界，底部单元节点固定，右侧远离爆炸端为固定边界.由于爆炸现象的高度非线性，模型边界设为不透水条件.通过应力初始化完成地应力平衡.

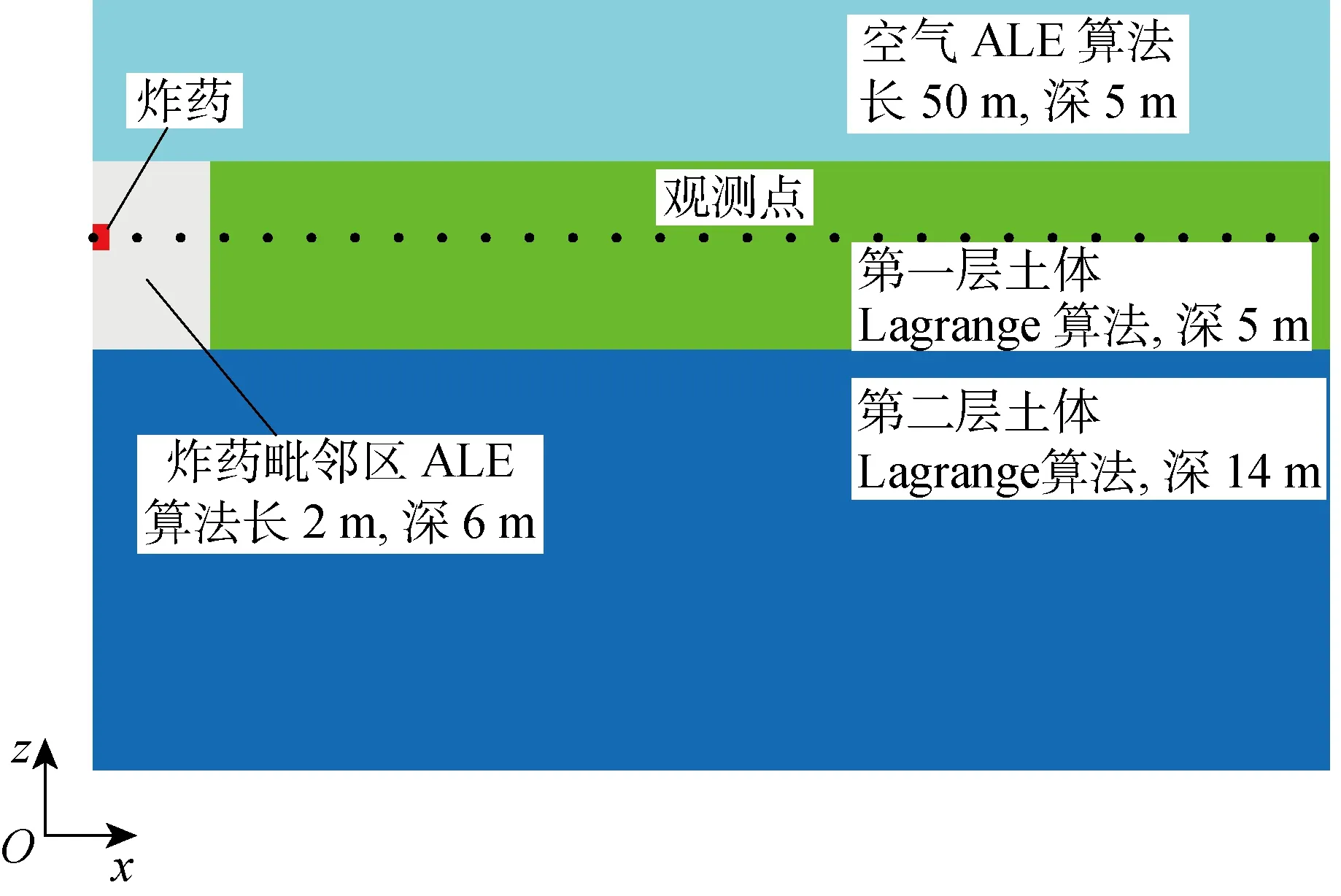
图1 土中爆炸原型模型Fig.1 Prototype model for underground explosion

高爆材料的起爆会释放巨额的能量，爆炸产生的高温、高压气体会在相邻介质中以爆炸波的形式向远方传递.爆炸波在多孔介质中随着传播距离的增大呈指数衰减，在lgσmax-lgls坐标系下，衰减曲线为直线，其中σmax为峰值应力，ls为等效距离.如图2所示，本文在验证模型中通过10 kg(绿色)和30 kg(蓝色)TNT当量的爆炸算例对模型进行校准.可以看到不同爆炸当量的模型计算所得峰值应力随传播距离均呈线性减小的趋势，计算所得衰减曲线与实验总结规律基本保持一致.在炸药10倍半径内，爆炸波的传播速度远高于介质声速，同时，饱和土中的爆炸波传播速度约为 1 200～1 500 m/s，很难捕捉到土体单元真正的应力峰值.所以考虑到计算结果的输出间隔有限，计算所得土单元的峰值应力的衰减曲线整体上会略低于实验规律，但误差结果较小可以接受.因此，将基于本文模型对地下钢顶管在爆炸荷载下动力响应的深入研究.

图2 爆炸应力峰值衰减校准图Fig.2 Peak pressure attenuation in saturated soil

3 结果与参数分析

对地下顶管的动力响应进行建模.如图3所示，模型由炸药、空气、土体和钢顶管组成.炸药的平面尺寸为1 m×1 m，模拟地面汽车炸弹，在炸药下方建立6 m×6 m×3 m的ALE土体区域.为了简化计算模型，对顶管周围土体采用一套参数，同时将地下水位设为与地表齐平.三维模型的边界条件采取底部固定，左右两侧及前后两侧仅允许z向位移.同时由于爆炸荷载的高度非线性，传播速度快，作用时间短，将模型边界设为不透水边界.研究参数为炸药当量、起爆位置、埋置深度(观测点至起爆点的z向距离)以及顶管管径.

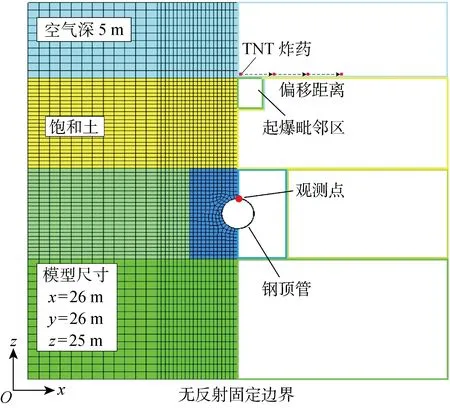
图3 计算模型简图Fig.3 Sketch of calculation model

图4分别为起爆点正下方6 m和15 m处的土体应力(σ)和孔隙水压力(p)的时程曲线.可以看到孔隙水压力与土应力的变化一致，在爆炸波波峰到达观测单元时，土应力和孔隙水压力骤升，稀疏波紧随爆炸压缩波之后，由于孔隙水不能受拉，孔隙水压力瞬间消散，由于土体单元在爆炸波的作用下整体处于受压状态，最终在土体单元应力的波动中，孔隙水压力又出现累积.

图4 起爆点下方土体应力和孔压时程曲线Fig.4 Time series of soil pressure and pore pressure below the explosion position

图5 不同炸药量下顶管最大竖向位移分布Fig.5 Distribution of peak z-displacement of pipe jacking under various explosive charges

首先分析炸药当量对于钢顶管的影响.在模型中，钢顶管上覆土厚8 m，顶管半径1 m，管壁厚2 cm.图5所示为不同炸药当量情况下顶管最大竖向位移(Sz)，其沿顶管轴向对称分布，且随炸药量的增加而线性增大.当炸药量达到600 kg时，顶管结构未出现位移突变，表明顶管仍在塑性变形阶段，未达破坏阶段.

爆炸波在土中指数衰减趋势，故上覆土对顶管起到一定保护作用.基于600 kg TNT，半径为1 m，管壁厚2 cm的钢顶管模型研究埋深(D)对顶管动态响应的影响.如图6所示，随着上覆土厚度的增大，-5～5 m范围内的顶管核心受压区的竖向位移明显减小.在目前爆炸当量下，埋深超过11 m时，上覆土对于钢顶管的保护作用开始减弱.当埋深仅为5 m时，-3～3 m范围内位移较大，而y=±5 m左右的顶管下方土体则起到了类似杠杆支点的效果，进而导致埋深5 m的钢顶管在6 m范围外的竖向位移反而较小.

图6 不同埋深下顶管最大竖向位移分布Fig.6 Distribution of peak z-displacement of pipe jacking under various embedment depths

图7 不同顶管半径最大竖向位移分布Fig.7 Distribution of peak z-displacement of pipe jacking under various pipe jacking radii

顶管管径(R)同样会对结构的动态响应造成影响.从图7可以看到，在顶管上覆土厚度为8 m，地面爆炸荷载为600 kg TNT当量的情况下，当顶管半径小于1.2 m时，顶管最大竖向位移分布相似.当顶管半径为1.5 m时，距离起爆点横向距离5 m以内出现明显塑性变形，并不断发展，最终结构局部破坏.而当顶管半径为2.0 m时，结构平面内结构破坏范围进一步扩大.

当地表爆炸荷载真正出现时，往往不会在顶管的正上方，所以本文对起爆点的偏移位置进行了讨论分析.研究模型中，钢顶管埋深8 m，顶管半径1 m，管壁厚度为2 cm，起爆点的偏移x=0，4，8，12 m，如图8所示.当偏移距离小于4 m时，顶管的竖向位移分布模式相似.而当偏移距离大于8 m时，钢顶管倾向于整体位移.需要指出的是，洋红色实线是起爆点的偏移距离12 m时的顶管最大竖向位移结果，洋红色虚线是起爆点偏移距离为12 m时顶管竖向位移最终稳定状态.可以看到顶管沿轴向竖向位移最终稳定状态(洋红色虚线)为正.炸药起爆后会在土体中产生体波和面波，体波传入土体深处，按照运动方式又分为P波和S波.P波在多孔介质中衰减较快，仅能在起爆点邻近土体中起到加固作用；而S波传播较远，会对土体产生扰动，同时爆炸区附近的土体压缩对远处的土中结构物起到了侧向挤压作用，这也就造成了偏移距离为12 m的算例中，最终稳定状态时顶管略微上浮(洋红色虚线).

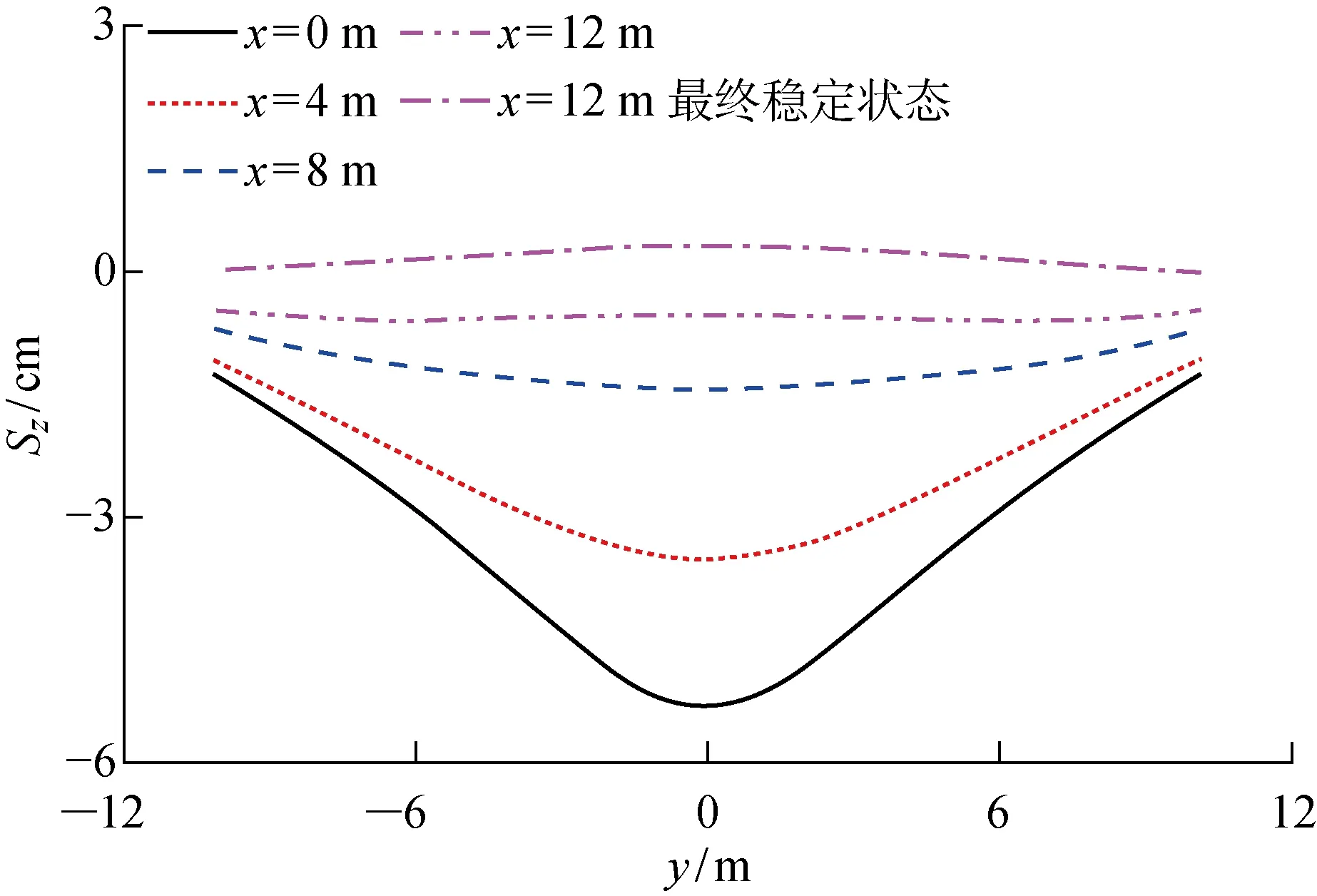
图8 不同起爆点偏移位置下钢顶管最大竖向位移分布Fig.8 Distribution of peak z-displacement of pipe jacking under various explosion offsets

此外，起爆位置的偏移会对钢顶管产生横向推力.如图9所示，起爆点在顶管正上方时，顶管也会产生少量的横向位移(Sx)，整体竖向向下运动.在偏移距离增至8 m的过程中，顶管沿轴线的横向位移逐渐变大，形态稳定.而当偏移距离为12 m时，在 -6～6 m范围内，顶管整体平移，平移量略小于偏移距离为8 m的算例.

图9 不同起爆点偏移位置下钢顶管最大横向位移分布Fig.9 Distribution of peak x-displacement of pipe jacking under various explosion offsets

4 结论

在本文中，通过将u-p模型植入有限元程序，实现水土耦合计算，建立了地表爆炸荷载作用下地下钢顶管的动态响应模型，通过将ALE-Lagrange的耦合算法解决爆炸荷载导致的网格畸变问题，进而对饱和土中地下钢顶管在地面爆炸荷载下的动态响应问题进行研究.随后基于前人实验规律对本文模型进行了验证，最后对炸药量、起爆位置、钢顶管埋置深度以及顶管半径等参数进行了参数分析.基于计算结果，可以得到如下结论：

(1) 将u-p模型嵌入有限元程序，实现了在高度非线性荷载作用下的水土耦合计算，可以用于研究沿海高地下水位地区地下结构物在爆炸荷载作用下的动态响应问题.

(2) 建立验证模型，通过已有实验数据对本文模型进行了验证，应力波在饱和土中指数衰减，与实验规律基本一致，证明了本文模型预测既有管线在爆炸荷载作用下的动态响应的可行性.

(3) 实验结果表明，在地下钢顶管结构局部破坏前，顶管竖向位移随炸药量线性增大；顶管竖向位移随上覆土厚度的增大而减小，埋深设为11 m左右，上覆土对顶管的保护效果较好，同时保证施工经济性.

(4) 顶管直径的增大会降低结构在地表爆炸荷载作用下的承载能力，随着埋深的增加需要对管线进行有效的力学分析，设计合理的管径和壁厚.

(5) 顶管最大竖向位移随起爆点偏移距离的增大而减小，当偏移距离为12 m时，顶管在爆炸波的作用下最终略微上浮，同时，顶管的横向位移也会随着偏移距离先增大后降低.