肠道微型仿尺蠖式机器人机载供能线圈优化
2020-03-09高晋阳颜国正石云波
高晋阳, 颜国正, 石云波, 刘 俊
(1. 中北大学 电子测试技术国家级重点实验室, 太原 030051; 2. 上海交通大学 仪器科学与工程系, 上海 200240; 3. 中北大学 先进制造技术山西省重点实验室, 太原 030051)
微型仿尺蠖式机器人对于湿滑、黏弹、游离的肠环境具有极好的适应性,是用于肠道疾病微创诊查的理想器件之一[1-8].该种机器人的运动机构包含1个伸缩子机构和2个位于其两端的扩张子机构.由于伸缩子机构直径较小,其外围空间常用于集成圆环形供能线圈[7,9-11],有效提高了机器人内部空间利用率,避免了采用传统实心圆柱形供能线圈引起机器人长度增加的问题[12].圆环形供能线圈一般由圆环形磁芯和绕组构成,根据绕组数量和排布方式分为一维[9-10]和三维[7,11].一维圆环形供能线圈只包含1个缠绕于圆环形磁芯上的绕组,具有占用空间小的优势,但需要配合可激发任意方向交变磁场的三维发射线圈使用,且需对供能线圈的实时姿态进行检测,因此实现难度较大.三维圆环形供能线圈包含3个正交排布的绕组,配合一维发射线圈即可实现任意姿态电能感应,比较容易实现.但其要求可用圆环形空间的内外径差大,以便为3个绕组提供充分的绕线空间.从机器人尺寸微型化的角度考虑,机载一维供能线圈和三维发射线圈的供能方案更具研究前景和价值.
目前,大部分机载一维供能线圈设计参数的选取通过实验比较方法来获得,线圈绕制形式为圆环形绕组长度基本等于圆环形磁芯长度,外径接近于机器人外径,以实现对空间的充分利用[7,11].然而,这种绕制形式供能线圈的绕组发热现象较为严重.作者在前期研究工作中提出了1种一维供能线圈的初步设计优化方法[13],通过优化绕组匝数和线径,有效避免了绕组发热现象,使得机载一维供能线圈的最大输出功率达到 1 130 mW.该研究的不足之处在于:① 绕组被简化为单匝绕线,即绕组中各匝绕线均被等效为具有同一几何参数的单匝绕线,未考虑各匝绕线几何参数差异造成的电参数差异;② 假设绕组位于磁芯轴向中心位置,未研究绕组轴向位置对输出功率的影响;③ 采用了绕组外径尽量靠近可用空间外径的缠绕原则,在该原则下绕组层数由可用空间和绕线线径唯一确定,未研究绕组层数对输出功率的影响.
本文在前期研究工作的基础上,对机载一维供能线圈进行进一步优化设计,分别对绕组中各匝绕线进行几何建模,考虑匝间差异性,通过优化绕组轴向位置和层数,进一步提高供能线圈的输出功率.首先,基于供能线圈内嵌磁芯,邻近机器人金属零件的特点,建立其集成环境模型;然后,借鉴磁性器件理论相关公式,确定供能线圈在该集成环境中各电参数的计算方法;最后,以最大化供能线圈输出功率(可由各电参数表征)为目标,以供能线圈温升安全(不高于42.5 ℃)和机器人内部可用空间为约束[13],完成对供能线圈绕组轴向位置、层数、匝数以及线径的优化.
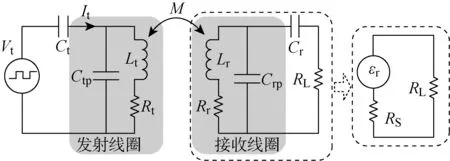
图1 无线电能传输系统等效电路Fig.1 Equivalent circuit of wireless power transmission system
1 无线电能传输系统介绍
图1所示为基于近场感应耦合原理的无线电能传输系统等效电路.图中:Vt、Ct、Ctp、Lt以及Rt分别为发射线圈驱动电压,使发射线圈谐振的调谐电容,发射线圈的寄生电容,发射线圈自感以及发射线圈的交流电阻;Lr、Rr、Crp、Cr以及RL分别为机载供能线圈自感,机载供能线圈交流电阻,机载供能线圈寄生电容,使机载供能线圈谐振的调谐电容以及负载电阻;M为发射线圈与机载供能线圈间的互感;εr为可感应产生交变电动势;RS为等效串联电阻.当Vt为方波时,由于发射线圈的选频作用,在发射线圈中产生正弦激励电流It,It=Imsin(2πft),Im为激励电流幅值,进而在发射线圈周围激发交变磁场.本文发射线圈采用前期研制的双层螺线管对结构,设计参数为:直径40 cm;长度20 cm;匝数25;激发交变磁场频率f=218 kHz;Im≤1.98 A[14].
机载供能线圈置于发射线圈激发的交变磁场中时Cr可使机载供能线圈处于谐振状态而呈现纯阻性,因此可将机载供能线圈等效为εr和RS串联连接的形式.机载供能线圈的εr、RS、输出功率PL、滞留功率PS的计算式为[15]
(4)
式中:T为交变磁场的周期,与It的周期一致;fs为机载供能线圈的自谐振频率,通常远大于f,故有RS≈Rr.

图2 机载供能线圈集成到仿尺蠖式机器人的典型环境Fig.2 Typical environment of the powering coil integrated to onboard the inchworm-like robot
2 机载供能线圈集成环境模型
图2所示为机载供能线圈集成到仿尺蠖式机器人的典型环境.圆环形磁芯安装在伸缩子机构的外围圆周空间,圆环形绕组缠绕于圆环形磁芯上,磁芯内部及两侧均有金属零件.圆环形磁芯对其内部金属零件具有屏蔽效果,因此可认为机载供能线圈仅受两侧金属零件影响,将两侧金属零件等效为两个金属圆板,得到图3所示的机载供能线圈集成环境简图,图中坐标原点O位于磁芯中心位置,各参数的定义见表1.
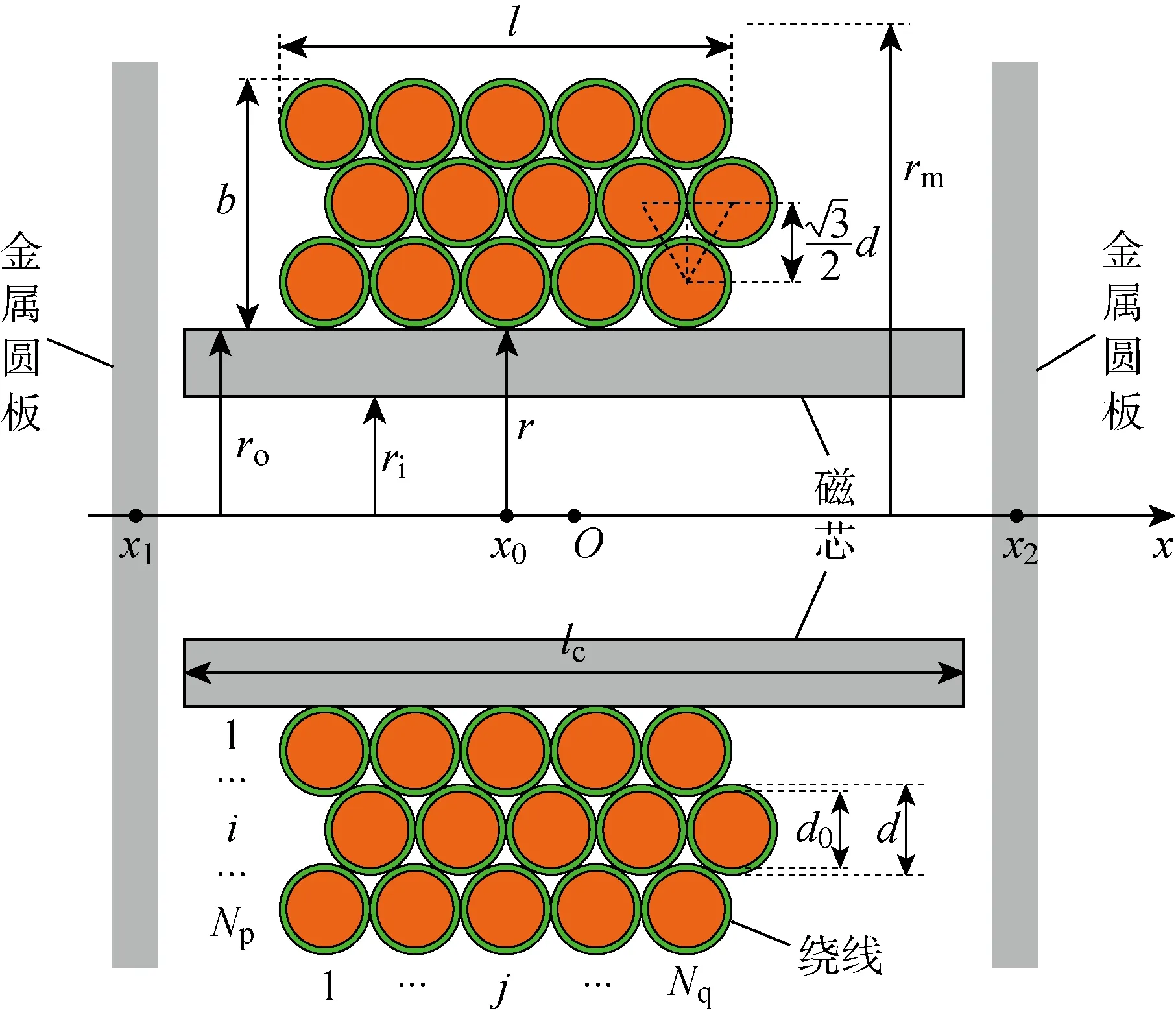
图3 机载供能线圈集成环境剖视图Fig.3 Section view of the simplified integrated environment of the powering coil

表1 机载供能线圈设计参数定义Tab.1 Design parameters definition of powering coil
2.1 圆环形绕组几何建模
本研究重点对圆环形绕组进行优化,优化对象包括x0、Np、Nt(或Nq)和d0,为此需明确绕组中各匝绕线的几何参数,即对各匝绕线进行几何建模.若某匝绕线在绕组中的第i层,第j匝(见图3),则该匝绕线的轴向位置xij和半径rij可表示为
xij=x0-l/2+jd
(5)
(6)
2.2 圆环形磁芯参数测定
磁芯在机载供能线圈中使用时,退磁效应严重,导致其实际磁导率远低于初始磁导率.此外,由于圆环形磁芯几何形状的特殊性,目前尚无关于其退磁因子的解析计算式.因此需通过实验测定圆环形磁芯的相对磁导率,表示如下:
(7)

(8)
0.013
(9)
由式(5)、(6)和(8)可计算缠绕于磁芯上的任意一匝绕线围成区域的有效磁导率为
(10)
式中:μ0为空气磁导率.
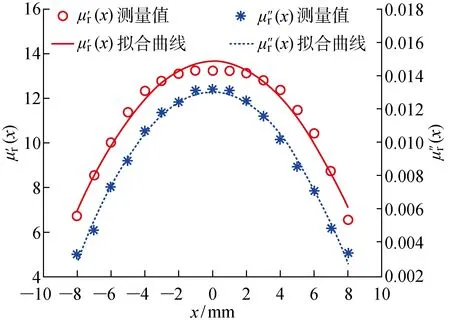
图4 圆环形磁芯相对磁导率测量结果和拟合曲线Fig.4 Measuring results and fitted curves of the ring-shaped ferrite core
2.3 金属圆板涡流效应影响分析
机载供能线圈感应交变磁场产生感应电动势后,激发二次交变磁场,使两侧金属圆板中产生涡流效应.为分析涡流效应对机载供能线圈的影响,将两侧金属圆板等效为两个短路圆线圈.显然,短路圆线圈与机载供能线圈同轴且对齐,由互感理论可知短路圆线圈将增加RS[16],增加量Rm近似计算如下:
Rm≈
(11)
式(11)中等号右侧两项分别表示位于x1,x2处的金属圆板造成的电阻增量.Re1、re1、Re2和re2为等效参数,由式(11)对多组Rm测量值进行最小二乘拟合确定.测量Rm时同样采用上节所用测试绕组和LCR测试仪,磁芯两侧有无金属零件时测试绕组的电阻差值即为Rm.对于图2所示的仿尺蠖式机器人,前侧零件组等效的金属圆板轴向位置为x1=-9.3 mm,等效参数拟合为:Re1=0.390 1 Ω;re1=6.7 mm.后侧零件组等效的金属圆板轴向位置设为x2=9.3 mm,等效参数拟合为:Re2=0.320 6 Ω;re2=6.7 mm.通过对比发现,后侧零件组的涡流效应较前侧零件组更为显著.
3 机载供能线圈电参数计算
由式(3)和(4)可知,对于特定的发射线圈和负载,确定M和RS关于机载供能线圈设计参数的表达式,即可分析机载供能线圈设计参数对PL和PS的影响,由此实现对机载供能线圈设计参数的优化.
3.1 互感计算
图5所示为双层螺线管对发射线圈和机载供能线圈的相对位置.其中,双层螺线管对发射线圈简化为两个圆环O1和O2,且环半径和两环轴向间距均为rt=20 cm;机载供能线圈以一匝半径为rij的圆环表示.双层螺线管对发射线圈可在其内部区域产生均匀磁场,因此可将机载供能线圈置于其中心位置进行分析,当二者同轴对齐时,由诺曼公式得到二者间的互感为[17]
(12)
式中:Mij为机载供能线圈绕组中第i层、第j匝绕线与发射线圈的互感;N0为发射线圈的匝数,N0=25.

图5 双层螺线管对发射线圈和机载供能线圈相对位置Fig.5 Relative position between the transmitting coil of the double-layer solenoid pair type and the onboard powering coil
3.2 等效串联电阻计算
由上文对机载供能线圈集成环境的分析可知,机载供能线圈的Rr不仅包括自身绕线铜损R1,还包括磁芯损耗R2和金属圆板涡流效应造成的电阻增加量R3.由式(2)可知,Rs≈Rr,故有
RS≈R1+R2+Rm
(13)
绕线铜损R1可由Dowell公式计算[18]:
(14)
式中:Rdc为绕线直流电阻;Z1为与绕线线径,趋肤深度及孔隙因子等有关的参数,详细计算见文献[18].式(14)等号右边第一项表示趋肤效应损耗,第二项表示邻近效应损耗.

(15)
4 机载供能线圈优化
机载供能线圈的优化以最大化输出功率为目标,同时还应对其绕组滞留功率进行限制,确保其温度低于42.5 ℃的安全限值:
(16)
式中:PS/l表示绕组单位长度的滞留功率.实验测量发现:当PS/l≤70 mW/mm时,可确保绕组温度不超过42.5 ℃[13].由式(3)可知,f、Im及RL给定时,PL仅与M和RS有关;再由式(11)~(15)可知,M和Rs与机载供能线圈设计参数(包括绕组轴向位置、层数、匝数及线径)有关.因此,通过优化机载供能线圈设计参数可使PL的值达到最大.
4.1 绕组轴向位置优化
由图4可知,绕组在磁芯不同轴向位置时的磁导率不同,导致M和R2不同.此外,由式(11)可知,绕组在磁芯不同轴向位置时,金属圆板涡流效应造成的Rm也不同.因此,需在式(16)的要求下,对绕组轴向位置进行优化.优化时选用的示例绕组的设计参数为:d0=0.15 mm;Np=4;Nq=10;RL=30 Ω.图6所示为绕组在磁芯不同轴向位置输出功率的测量装置.机载供能线圈整体安装在仿尺蠖式机器人上,且绕组可沿磁芯轴向滑动.机器人置于发射线圈中心位置,绕组感应发射线圈激发的交变磁场产生感应电动势,感应电动势经整流后,由双绞线加载到负载电阻两端.万用表测量负载电阻两端电压,以获得输出功率.

图6 绕组在磁芯不同轴向位置输出功率的测量装置Fig.6 Experimental setup for measuring the output power of the ring-shaped winding at different axial locations
图7(a) 所示为由式(3)~(15)所计算绕组在磁芯不同轴向位置时PL、PS/l的值以及PL的测量值.可以发现:① -5 mm≤x0≤5 mm时,PL的计算值和测量值基本吻合;在该范围之外,即绕组靠近两侧金属圆板零件时,PL计算值和测量值偏差逐渐增大.②x0=-0.2 mm时,PL最大,x0=1.3 mm时,PS/l最大,这表明当两侧金属圆板零件造成的涡流效应不同时,绕组应由磁芯中心向涡流效应小的金属圆板零件偏移.由于此处偏移仅为0.2 mm,在下文优化中可认为磁芯中心位置为绕组最优轴向位置.
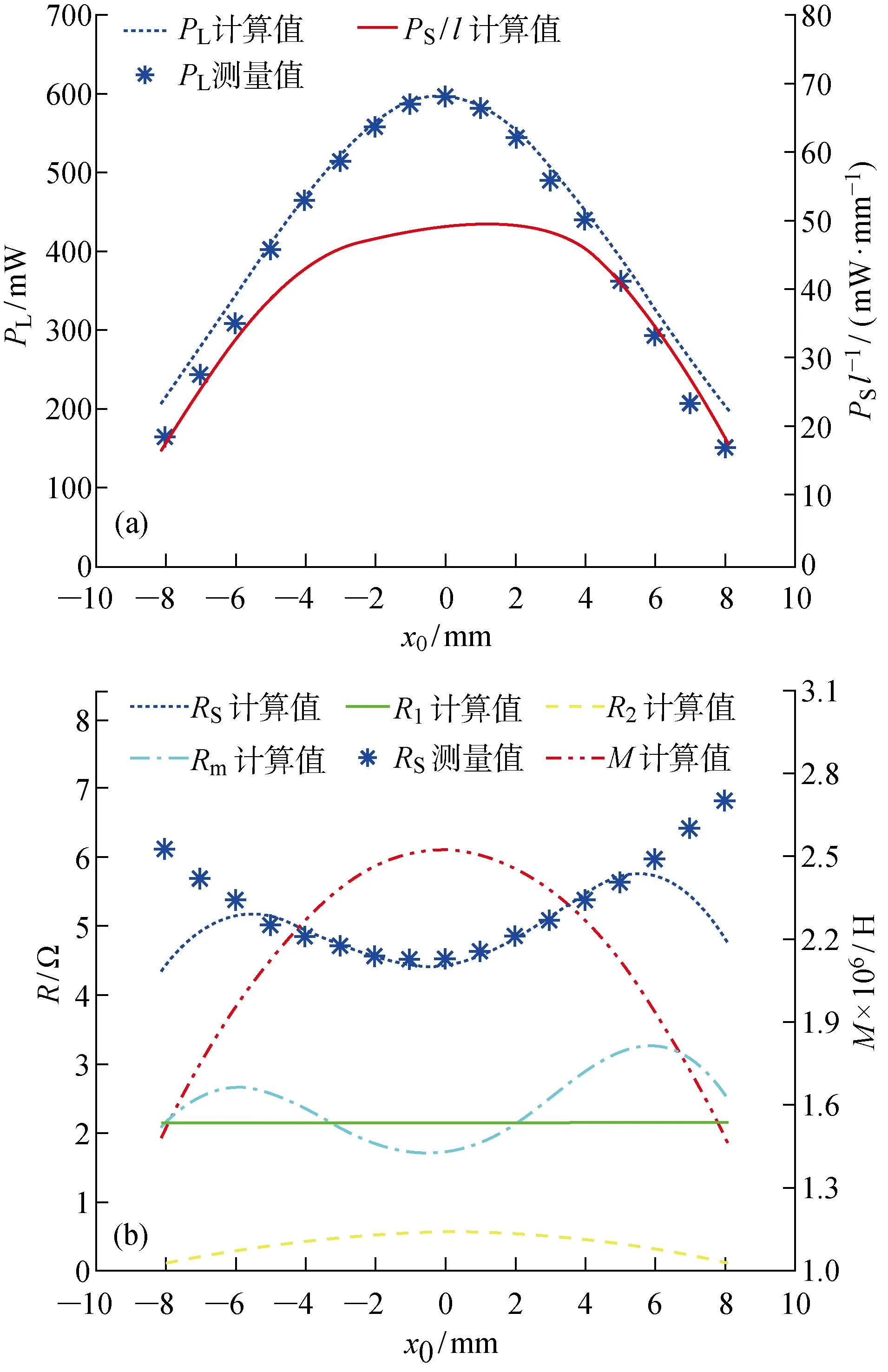
图7 绕组在磁芯不同轴向位置时各参数的计算值和测量值Fig.7 Calculated and measured results of key parameters of the ring-shaped winding at different axial locations
图7(b) 所示为绕组在磁芯不同轴向位置时,RS的计算值和测量值以及R1、R2、Rm、M的计算值.可以发现:① -5 mm≤x0≤5 mm时,RS的计算值和测量值基本吻合;在该范围之外,当RS的计算值减小时,其测量值反而增加, 原因在于Rm的计算式(11)在导出过程中进行了简化,导致其不能准确计算绕组靠近两侧金属圆板时涡流效应造成的电阻增加量,式(11)的这一局限性也解释了图7(a)中绕组靠近两侧金属圆板零件时,PL计算值和测量值偏差逐渐增大的现象.由于绕组在靠近两侧金属圆板零件时PL急剧减小,因此实际设计时,绕组应尽量置于磁芯中间位置,这时式(11)仍适用.②相较于R1(定值)和Rm,R2的值较小,使得RS和Rm呈现基本相同的变化规律.③RS和M呈现相反的变化规律,两者在x0=0附近分别取得最小和最大值,因此使得PL的值达到最大.
4.2 绕组层数优化
由上节对绕组轴向位置优化可知,绕组在磁芯中心位置附近时,输出功率可达到最大值.为简化分析,本节对绕组层数优化时,假定绕组轴向位置为x0=0.绕组层数优化还需满足几何约束:

(17)
设立绕组长度约束l≤10 mm的原因为确保式(11)对Rm的计算准确性,绕组厚度约束b≤1 mm确保绕组直径不超过机器人直径.表2所示为d0=0.15 mm、Nt分别为40、50、60、70以及80时,PL和PS/l在不同Np下的计算结果.可以发现:①Nt一定时,PS/l随Np的增加而增加;Np一定时,PS/l随Nt的增加而增加,即Np和Nt的增加均会加剧绕组温升;反之,温升安全性将限制Np和Nt取值上限.②Nt分别为40、50、60及70时,满足设计要求的最优层数(Np-o)均为2,相应的最大输出功率(PL-o)分别为594.1、839.0、1 079.7及 1 300.2 mW,即PL-o随Nt的增加而增大;然而,Nt的增加会加剧绕组温升,当Nt=80时,PS/l已超过70 mW/mm的安全限值.

表2 Nt和Np取不同值时,PL和PS/l的计算结果Tab.2 Calculated results of PL and PS/l when Nt and Np take different values
注:① “—”表示Nt不能被Np整除,即单层匝数Nq不能取整的情形;
② “”表示绕组长度l超过10 mm的情形;
③ 灰色填充区域表示单位长度滞留功率PS/l>70 mW/mm的情形.
4.3 绕组匝数和线径优化
在式(16)和(17)的约束下,对绕组匝数及线径进行优化.Nt的考察范围为0~100,d0选取工程中的常用线径0.10、0.12、0.15、0.18、0.20以及0.25 mm,并假定绕组轴向位置为x0=0.优化时,基于上节层数优化方法,确定各d0下,与不同Nt对应的Np-o和相应的PL-o,通过比较PL-o的优化结果,实现Nt和d0优化.图8所示为不同d0时,PL-o和Np-o随Nt增加而变化的曲线.可以看出:① 由于式(16)对PS/l的限制,Nt的取值上限均未达到考察范围上限100.② 随着Nt增加,PL-o基本呈增加趋势,直至达到Nt的取值上限;而Np-o基本呈减小趋势(d0=0.25 mm除外),这主要是由于Nt的增加会加剧绕组温升,而减小Np是减缓绕组温升的有效途径.③ 当Nt≤30时,d0对PL-o的影响很小;当Nt>30时,随着Nt增加,线径d0=0.15,0.18,0.20,0.25 mm对应的PL-o曲线基本重合,且显著大于d0=0.10,0.12 mm对应的PL-o曲线,表明d0≥0.15 mm时有利于提高PL-o.依据图8的计算结果,确定绕组各设计参数的优化值为:d0=0.20,Nt=84;Np-o=2,相应PL-o=1 586.2 mW.

图8 不同d0时PL-o及Np-o随Nt的变化曲线Fig.8 Changing of PL-o and Np-o with Nt under different d0
按上述设计参数制作了尺寸为∅(12.0~12.4) mm×9.9 mm的绕组,并采用图6所示实验装置测得其集成到仿尺蠖式机器人的输出功率为 1 478.3 mW,与计算值偏差约为108 mW,考虑手工绕线及测量误差,这一偏差在可接受范围之内,表明本文提供的分析方法可有效指导机载供能线圈的设计优化;此外,文献[13]中通过优化绕组匝数和线径使最大输出功率达到 1 130 mW,本文所得输出功率值较文献[13]提高近340 mW,表明在优化绕组匝数和线径的同时,优化绕组层数可进一步显著提高机载供能线圈的输出功率.
5 结语
本文对机载一维供能线圈进行了设计优化.首先,考虑仿尺蠖式机器人内部集成环境的特殊性,建立了机载供能线圈集成环境模型,量化了集成环境对线圈电参数的影响.然后,给出了特殊集成环境中线圈的互感和等效串联电阻的计算方法.接着对机载供能线圈的绕组轴向位置、层数、匝数和线径进行优化,获得了各设计参数选取的一般性结论.最后,基于参数优化结果制作了机载一维供能线圈,其绕组尺寸仅为∅(12.0~12.4) mm×9.9 mm,当位于磁芯轴向中心位置时,输出功率高达 1 478.3 mW.本文将为仿尺蠖式机器人机载供能线圈的快速设计优化提供理论和方法依据.
