基于网络最大流的作者同名区分算法
2020-03-09全锦琪傅洛伊甘小莺王新兵
全锦琪, 傅洛伊, 甘小莺, 王新兵
(上海交通大学 电子信息与电气工程学院, 上海 200240)
随着互联网技术的快速发展,大量学术论文以电子文档的方式保存在各出版社的电子数据库中,如ACM电子数据库(DL)、IEEE DL、Springer数据库等.为了方便研究人员对不同数据库中的论文进行统一检索,很多学术搜索引擎也随之产生,如谷歌学术、微软学术、DBLP、Acemap等.通过这些学术搜索引擎,研究人员可以快速精准地检索出自己想要的论文,不仅可以通过标题进行精确检索,也可通过关键词进行模糊检索,还可以按照学者姓名检索出该学者发表的所有论文.
然而,由于许多学者可能拥有完全一样的名字,即学者的名字具有歧义性,给学术搜索引擎在数据整合及检索上带来很大的困扰.在学术论文数据整合过程中,若不能很好地对同名学者进行区分的话,那么当用户想检索某一位学者发表的所有论文时,往往得不到精确的结果.另外,目前也有许多研究人员从事针对学者的数据挖掘研究,例如学者师承关系挖掘、学者未来影响力预测等.这些研究都需要以能够精准获得某位学者发表过的所有论文为前提.因此,对同名学者的区分具有很重要的研究意义.
目前,已有许多国内外的研究人员对学者同名区分问题展开了研究.Yin等[1]提出了同名区分框架DISTINCT,该框架结合Jaccard系数及随机游走来计算集合的相似度,利用支持向量机(SVM)训练出各特征的权重,再进行层次聚类.Tang等[2]提出一种基于隐马尔科夫随机场的模型,模型每次迭代分配标签,寻找出最大化后验概率的分配方案.Fan等[3]提出了基于图论的GHOST框架,该框架首先取得两点间k跳内的所有简单路径,然后按照规则剔除无效边,再采用仿射传播算法进行聚类.另外,网络嵌入(Network Embedding)[4]研究领域近年来备受关注,学者们相继提出了DeepWalk[5]、LINE[6]和node2Vec[7]算法.Zhang等[8]将Network Embedding的思想用于同名区分,通过最大化有边相连的节点间的向量内积训练出论文的向量化表示,再采用K-Means算法进行聚类.
尽管目前已存在一些针对学者同名区分的研究成果,但对非常大众化的学者名(如Wei Wang),特别是在同一个机构存在多个同名不同人的学者,或是同名不同人的学者在同一会议发表过文章等复杂情况下,现有方法不能很好地进行同名区分,会造成精准率偏高但召回率偏低,或是召回率偏高但精准率偏低等问题.本文提出基于网络最大流的同名区分(MFND)算法,能够有效地降低不同学者实体之间的共享特征(机构、发表会议等)给同名区分带来的影响,从而达到更好的同名区分效果.
1 问题定义
本文研究的是如何解决学者同名的区分问题.学者同名区分指的是对包含同一个学者人名的论文进行区分,根据人名指代的真实实体不同将论文集合划分成若干子集合.形式上,即给定一个学者人名,以及作者列表中包含该人名的论文集合P={P1,P2,…,PI},求P的划分方式Dk={D1,D2,…,DK},使得P为同名但不同人的真实学者实体所发表的论文集合.某作者与论文关系图示例如图1所示.其中,A1、A2、A3是同名不同人的3位真实作者.
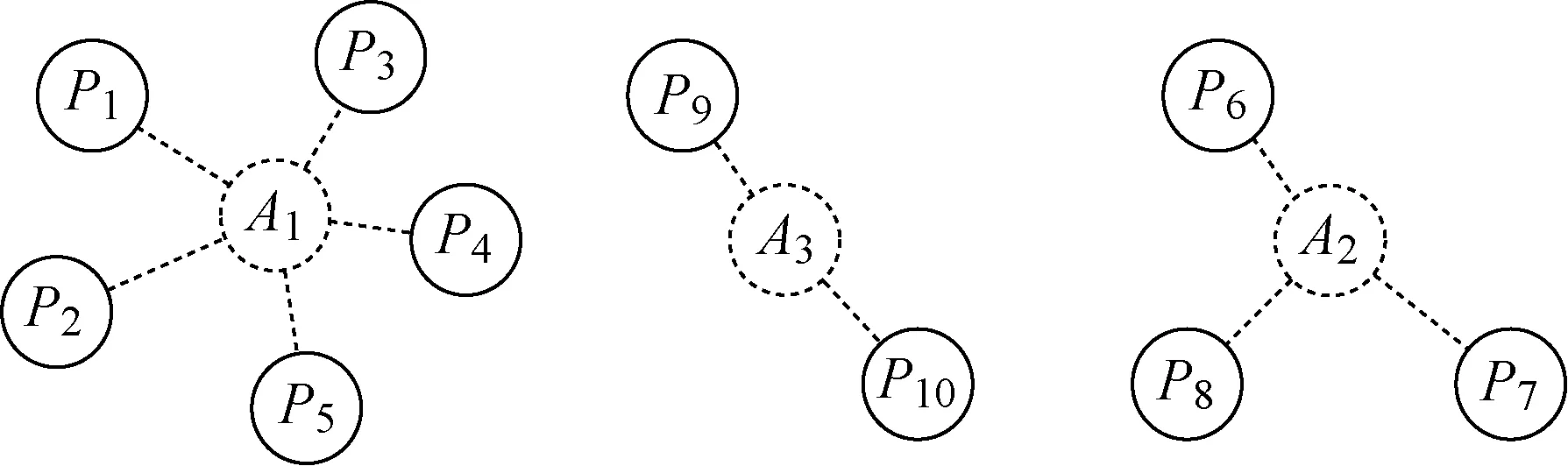
图1 作者与论文关系图Fig.1 The relationship between authors and papers
图1中Pi(i=1,2,…,10)与Am(m=1,2,3)的对应关系是真实正确的.然而在进行同名区分之前,无法得知有多少个同名的作者实体Am,更无法知道Pi与Am的真实对应关系,故图中采用虚线表示.那么,同名区分的目标在于将论文节点Pi进行聚类,使得同一位作者所写的论文尽可能地聚到同一类中,每一类代表一个真实作者实体Am所写的论文集合.
2 MFND算法
2.1 基本思路
首先,可以把同名区分问题转化为异构网络图[9]中的聚类问题.异构网络图即为拥有多种不同类型节点和边的网络图.若将待区分的学者名字对应的所有论文,以及论文的合作者、所属机构等特征提取出来融合在同一网络中,可形成一张异构网络图.例如,将图1中的论文及其特征融入一张图中,可形成如图2所示的异构网络图.其中:Cq(q=1,2,3,4)表示合作者;Op(p=1,2,3)表示机构;Vr(r=1,2,3)表示论文发表所在的会议/期刊.在真实的聚类情况中,(P1,P2,P3,P4,P5),(P6,P7,P8),(P9,P10)分别同属于一个类.而同名区分的目标在于,在不知道真实类的情况下,如何将论文节点Pi进行聚类.
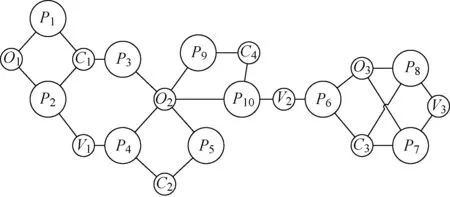
图2 学术异构网络关系图Fig.2 Academic heterogeneous relationship network
聚类的关键之一在于如何计算Pi和Pj的相似度sim(Pi,Pj).由图2可知,P3-P5和P9-P10都拥有一个共同特征O2.而这种不同真实类之间共享的特征,会给相似度的计算带来很大的困扰.例如,若采用随机游走的方式,则从源节点到目的节点产生的随机游走路径越多,两节点间的相似度就越高.从P4出发,可产生许多随机游走路径到达P2,同样也可以产生几乎等量多的路径到达P9(见图2).这就导致基于随机游走的相似度计算方式无法很好地区分开sim(P4,P2)和sim(P4,P9)的大小差异.
基于此观察,采用基于网络最大流的方式计算相似度,可降低不同真实类之间的共享特征带来的影响.具体而言,为了避免特征节点(Cq/Op/Vr)被重复用于提高相似度,给每个特征节点设定容量(初始化容量均为1,后续步骤会采取策略更新),再计算论文节点Pi两两之间的最大流量.例如在图2中,特征节点设定容量为1后,可通过计算获得P4-P2的最大流量为2,而P4-P9的最大流量为1,两者具有较明显的大小差异.
2.2 计算所有论文节点对的最大流
采用基于网络最大流的方式计算相似度,需计算论文节点Pi两两之间的最大流.而常用的最大流算法,如Edmonds-Karp[10]等算法,仅用于边有容量的网络.因此,需要将节点容量转换成边容量.将所有带有容量限制的特征节点Xs(Cq/Op/Vr),拆分成Xs_in和Xs_out两个节点,并添加有向边(Xs_in,Xs_out),使边容量c(Xs_in,Xs_out)等于原始节点容量c(Xs).对于原本与Xs相连的每个论文节点Pi,添加(Pi,Xs_in)和(Xs_out,Pi)两条有向边.将图2中的C2节点展开为如图3所示的形式.
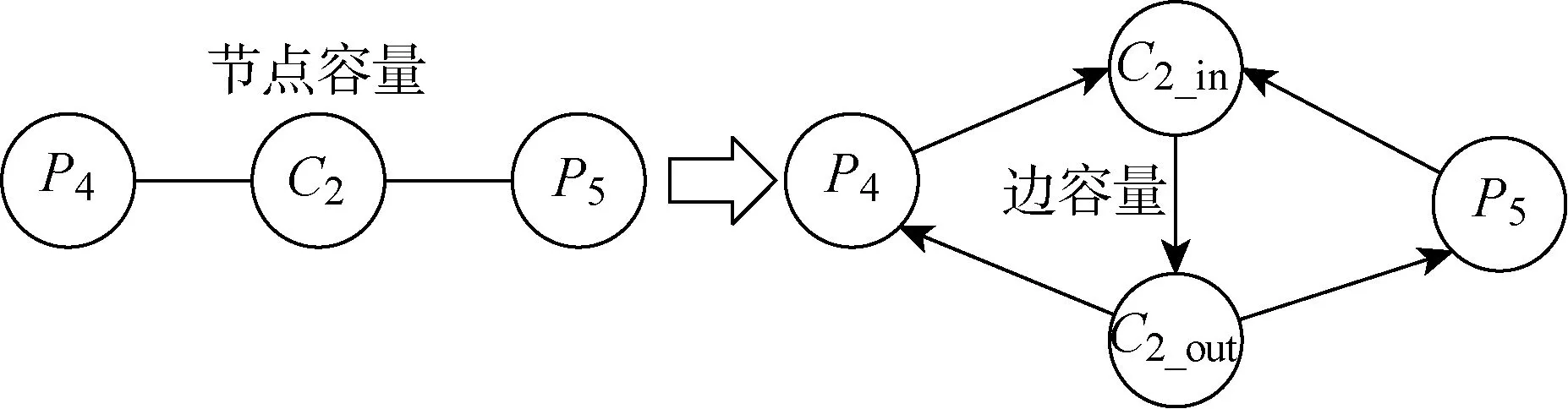
图3 节点容量转化为边容量示意图Fig.3 Diagram of changing vertex capacity to edge capacity
虽然将节点容量转换成边容量后,整个网络从无向图变成了有向图,但只从Pi节点来看,整个网络图依然是对称的,即Pi到Pj的最大流等于Pj到Pi的最大流.因此,可采用Gomory-Hu算法[11]计算所有Pi节点对的最大流.
若是每两个节点都计算1遍最大流,则需要计算I(I-1)/2次最大流.而Gomory-Hu算法通过求解Gomory-Hu 树就可以获得所有节点对之间的最大流,只需要计算I-1次最大流,大大地降低了时间复杂度.Gusfield[12]提出了一种更容易实现的 Gomory-Hu树求解方式.基于文献[12] 的算法思想,计算所有论文节点对的最大流.具体算法如下.

算法1求解所有论文节点对的最大流
输入G(V,E),论文节点集合Pi∥G为一个图;V为图G中的顶点集合;E为图G的中边集合
输出论文节点两两之间的最大流
(1) Initial Visited←{}
(2)r←rand(P) ∥随机选取一个论文节点设为星型树的中心r
(3) for eachi∈P-{r} do
(4) Tree[i]←r∥将其他论文节点与r相连
(5) for eachi∈P-{r} do ∥论文节点i为源节点
(6)j←Tree[i] ∥j为在星型树中与论文节点i相邻的节点,并将j作为目的节点
(7) cut, partition←MinimumCut(i,j) ∥计算最小割cut及割集partition
(8) Flows[i,j]←cut, Flows[j,i]←cut ∥记录论文节点i与j之间的最大流
(9) for eachkin the same partition asido ∥对于与论文节点i在同一割集的每个节点k
(10) ifk∈Pandk∉Visited and Tree[k]=j∥若k是未访问过的论文节点且与j相连
(11) Tree[k]←i∥在星型树中将k与论文节点i相连
(12) for eachm∈Visited-{j} do
(13) if cut < Flows[i,m]
(14) Flows[i,m]←cut, Flows[m,i]←cut
(15) Visited←Visited∪i∥论文节点i标为已访问
(16) return Flows
2.3 更新特征节点容量
为了更进一步限制不同真实类之间的共享特征(见图2中的O2和V2)带来的影响,可以为不同特征节点赋予不同的容量.直观来看,若一个特征节点被越多越大的真实类所共享,其容量应该越小.基于此想法,所设计的容量更新策略为:在得到基于初始化容量(均为1)的两两论文节点间的最大流后,计算特征节点的所有邻居可组成多少个内部(两两节点之间)流量大于1的连通子图.将连通子图内的节点个数记录为Sl,将所有l个连通子图内的节点个数s记录为序列[Sl],再基于序列[Sl]按照下式进行容量更新:
(1)
例如在图2中,O2的邻居有P3,P4,P5,P9,P10.经过初始化容量1的最大流计算之后,这些邻居可组成(P1,P2,P3,P4,P5),(P9,P10)两个内部流量大于1的连通子图,则[Sl]序列为[3,2].根据式(1),O2的容量将被更新为 0.069 7.同样,O3的容量将被更新为0.25,远大于O2的容量.下面给出更新特征节点容量的具体算法描述.

算法2更新特征节点容量
输入G(V,E),特征节点x, 论文节点间的最大流Flows
输出更新后的特征节点容量
(1) Initial Visited←{}, cap←1
(2)Z←neighbors(x) ∥获取节点i的邻居集合
(3) for eachz∈Zdo
(4) ifz∉Visited
(5)s←1, Visited←Visited∪z
(6) for eachy∈V-Visited do
(7) if Flows[z,y]>1
(8)s←s+1
(9) cap←cap/[2+lb(1+s)]
(10) return cap

2.4 聚类策略
在获得论文节点间的最大流后,可将最大流量作为节点相似度进行层次聚类(HAC)[13].将每个论文节点当成不同的单个类簇,然后重复合并相似度最高的两个类簇.基于节点间的相似度衡量类簇间的相似度有单连接(SL)、全连接(CL)以及平连接(AL)3种方式,分别是将两个类簇的相似度定义为两个类簇中节点间相似度的最大值、最小值和平均值.
由于采用最大流量作为相似度的衡量方式,两个类簇之间的最大、最小和平均节点间最大流均相等,即采用SL、CL、AL 3种方式均等价.因此,本文采用易于实现且时间复杂度更低的SL方式,每次合并相似度最大的两个论文节点所在的类簇,直到类簇的数量小于等于用户设定的聚类个数(K),合并结束后每个类簇就代表一个同名不同人的真实学者所发表的论文集合.在实验中将采用真实数据中的同名不同人的作者数作为聚类个数.
2.5 MFND算法
综上所述,下面给出MFND算法的步骤总结.
(1) 提取论文特征,将特征节点与论文节点融合成一张网络关系图;
(2) 为每个特征节点设定初始化容量(均为1);
(3) 根据算法1计算论文节点两两之间的最大流量;
(4) 根据算法2更新特征节点容量,并再一次计算论文节点间的最大流量;
(5) 根据最大流量对论文节点进行层次聚类.
3 实验与结果分析
3.1 实验数据集
由于同名区分解决的是论文与真实作者之间的匹配问题,为了验证该算法的有效性,需要论文与作者真实匹配的数据集.此前,Aminer发布了一个同名区分数据集[2],包含论文与作者的真实匹配关系.由于该数据集中机构名与会议/期刊名未归一化,所以通过将其中的论文标题和作者名与MAG(Microsoft Academic Graph)[14]进行匹配来构造一个新的数据集,即采用Aminer数据集所提供的论文与作者的匹配关系,而论文特征则用MAG所提供的特征.选取匹配后的10个对应文章数最多的作者姓名进行实验,统计数据如表1所示.
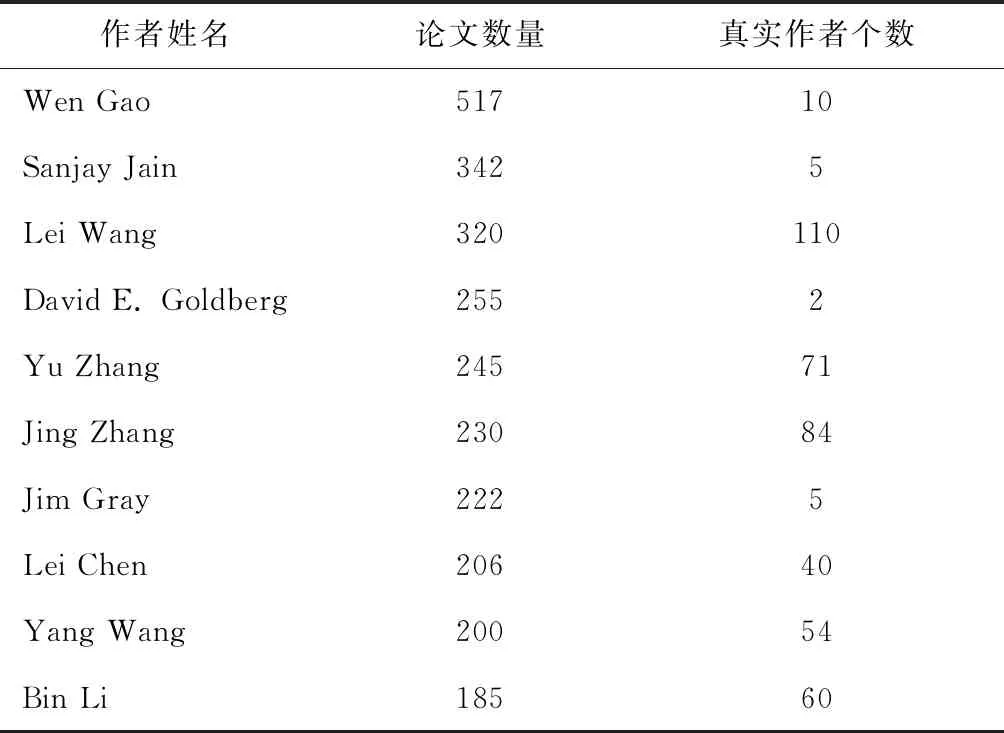
表1 数据集统计数据Tab.1 The statistics of dataset
3.2 实验设置
实验采用PairwisePrecision,PairwiseRecall和PairwiseF1作为评价指标,
PairwisePrecision=TP/(TP+FP)
(2)
PairwiseRecall=TP/(TP+FN)
(3)
PairwiseF1=
(4)
式中:TP表示真实属于同一类且预测分配到同一类的对数;FP表示真实不属于同一类但预测分配到同一类的对数;FN表示真实属于同一类但预测分配到不同类的对数.PairwisePrecision越高代表越多同一个类中的文章是真实属于同一人的,PairwiseRecall越高则代表越多同一人写的文章聚到同一个类中.PairwiseF1为PairwisePrecision和PairwiseRecall的调和平均数,PairwiseF1越高代表综合性能越好.
为了有效验证MFND算法的性能,选择以下3种方法进行对比.
(1) 将整个网络当成同构网络,使用Node2Vec算法[7]训练得到节点的向量化表示,再分别采用Single-Link和Average-Link两种方式的层次聚类进行聚类.
(2) 采用文献[8]中公开的源码实现.由于文献[8]中只使用了合作者的特征,为了公平起见,本文进行了两组对比实验,其中一组只使用合作者特征,而另外一组则使用合作者、机构和论文发表所在的会议/期刊3种特征.
(3) 获取Aminer官网中同名区分后的论文与作者对应关系并进行对比.该网址的同名区分是根据文献[2]中的算法实现的.
3.3 实验结果
算法对比实验结果如表2和3所示.表2为只使用合作者特征的实验结果,表3为使用了合作者、机构和论文发表所在的会议/期刊3种特征的实验结果.其中:“Node2Vec-SL”和“Node2Vec-AL”均表示采用Node2Vec算法,“-SL”表示采用单连接层次聚类,“-AL”表示采用平连接层次聚类;“MFND”表示所提出的完整算法;“MFND-R”表示去掉第4步骤后的算法.σ为精准率;ε为召回率;F1为精确率和召回率的调和平均数;AVG为平均数;A2为文献[2]中所提算法;A4为文献[4]中所提算法.
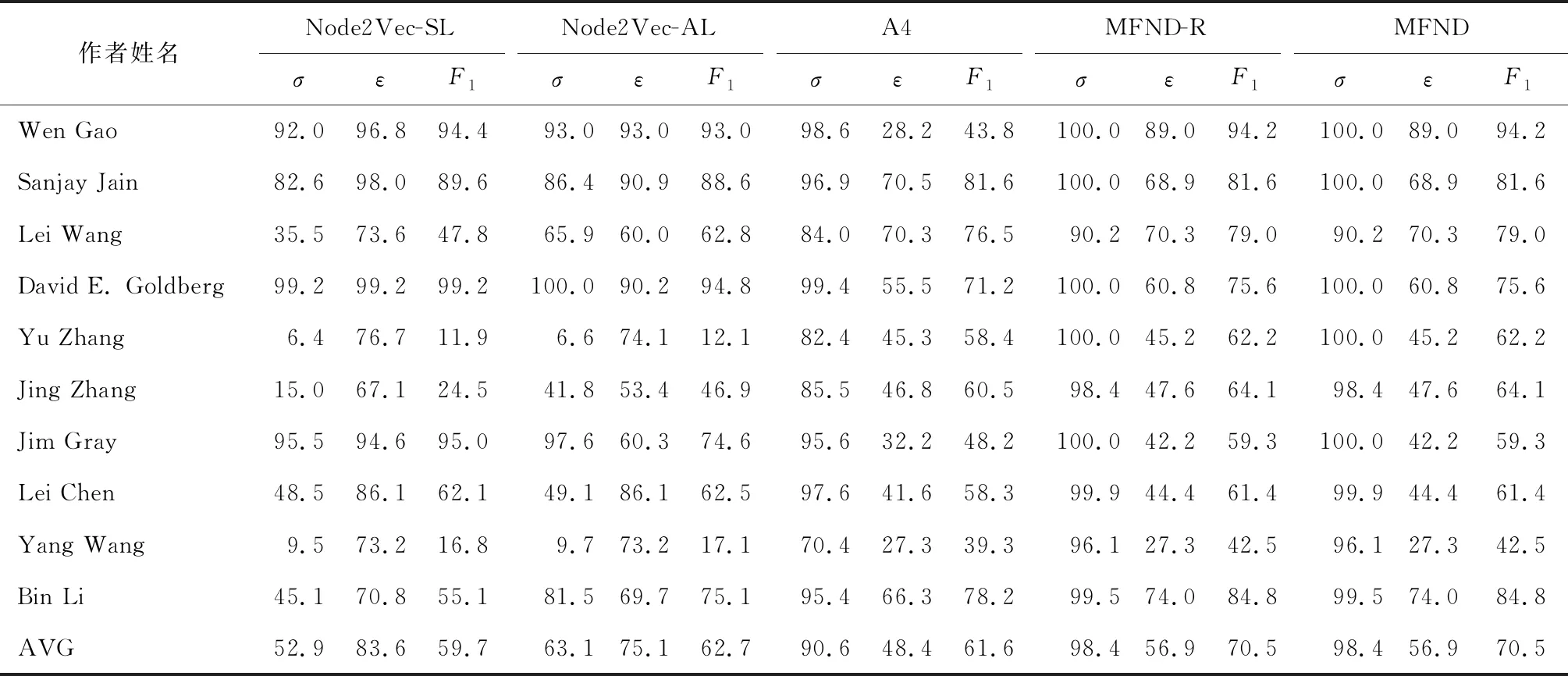
表2 使用合作者特征的同名区分结果Tab.2 Result of name disambiguation using co-author feature
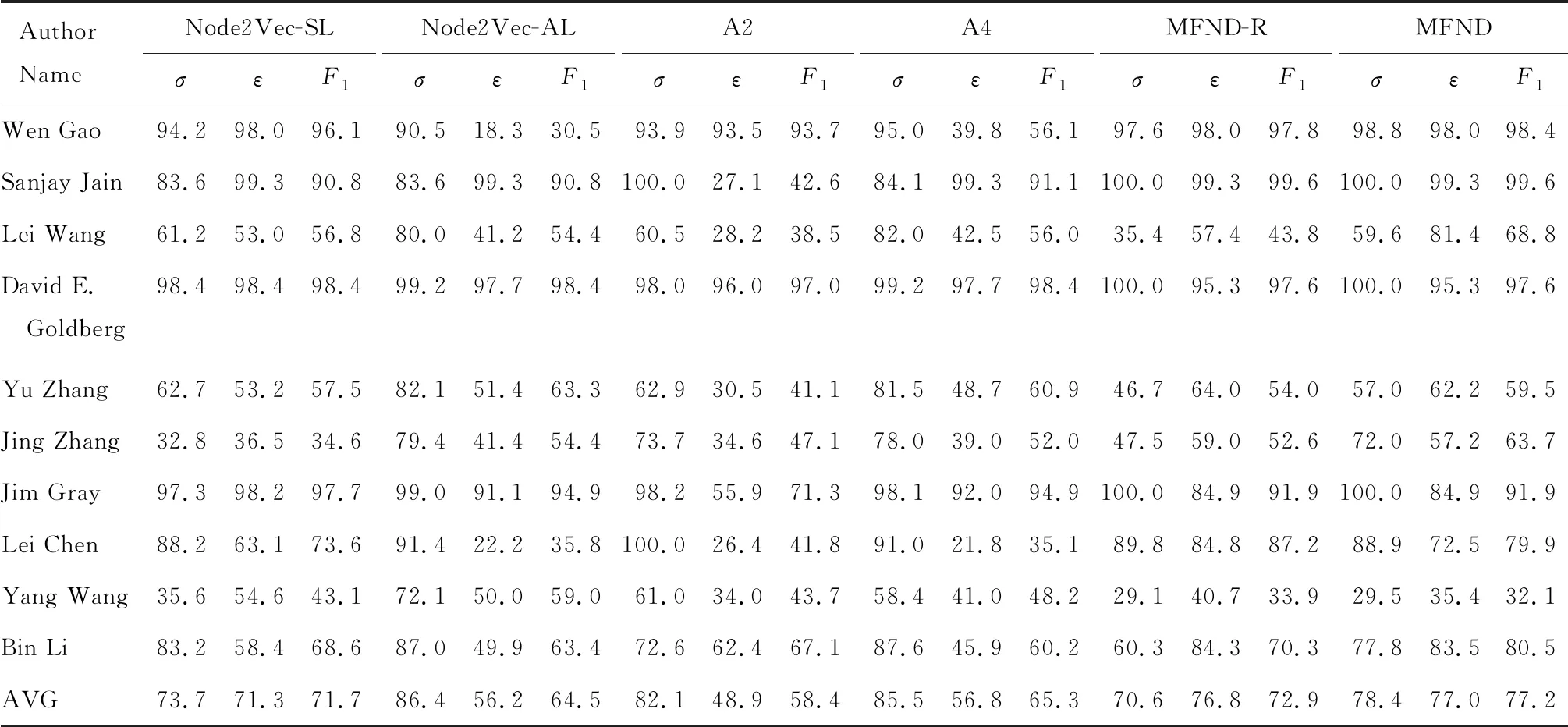
表3 使用合作者、机构、论文发表所在的会议/期刊3种特征的同名区分结果Tab.3 Result of name disambiguation using features of co-author & organization & venue of publication
由表2可知,去掉第4步骤后的MFND-R算法与采用完整步骤的MFND算法效果相同,均要优于其他算法,并且精准率高达98.4%.这说明“合作者”这一特征能够很好地区分不同作者所写的文章,是否采用第4步骤更新容量对算法结果影响不大,但MFND-R和MFND算法的召回率偏低,说明仅使用“合作者”这一特征很难将同一个人所写的文章全部聚在一起.
将表2和表3对比来看,使用3种特征的同名区分效果优于只使用合作者一种特征.由表3可知,Node2Vec-AL、Aminer以及ZHANG的算法取得了较高的精准率,但召回率较低,这说明同一个人所写的文章可能分散成多个类.采用Single-Link层次聚类的Node2Vec-SL则拥有较为均衡的精准率和召回率.而MFND算法同样在精准率和召回率上较为均衡,且综合性能更好.另外,对比MFND-R和MFND算法可以发现,加入“机构”和“论文发表所在的会议/期刊”特征后,采用第4步骤更新容量能够有效提高精准率,进而提升综合性能.
4 结语
本文提出一种基于网络最大流的同名区分(MFND)算法.该算法将论文及其特征(合作者、机构等)融合成一张网络图,根据特征节点的被共享程度设定不同的容量,再计算论文节点间的最大流量,并基于最大流量进行聚类.实验结果表明:与现有的同名区分算法相比,MFND算法在精准率和召回率上有较为均衡的表现,综合性能更好.
