自动存取系统多载量轨道小车避碰调度方法
2020-03-09马昌谱周炳海
马昌谱, 周炳海
(1. 同济大学 机械与能源工程学院, 上海 201804; 2. 桂林航天工业学院 管理学院, 广西 桂林 541004)
轨道小车(RGV)被广泛应用于自动化存取系统(AS/RS)[1].作为AS/RS的主要存取部件,一次能够搬运多个物品的RGV,即多载量RGV能提高系统的作业能力,其作业效率直接影响系统的吞吐率,因此,RGV的合理调度对系统性能有着非常重要的影响.在多车AS/RS中,RGV的调度不仅要考虑多货物同时载运的装卸顺序约束,还须考虑多车之间的碰撞问题,这是RGV调度的难点.
目前,关于RGV的研究主要聚焦于其设计、控制、派遣规则及路径选择等方面.Zheng等[2]设计了环形共轨RGV,并将其应用于分载系统.Lee等[3]构建了AS/RS仿真模型,确定了RGV的最优数量和导出系统吞吐率最大化策略.Lee和Chen等[4-5]研究了RGV的调度和系统控制问题,设定RGV的分派规则,并用仿真实验对其规则做了评价.Dotoli 等[6]应用着色Petri网,分析货物搬运系统并建立模型,提出控制策略,解除环轨RGV的死锁问题.Liu等[7]使用仿真实验,提出双RGV系统的两种作业策略,并分析了两者的优劣.RGV的调度方面,Kung等[8]将订单分为不同的集群,按照规则将订单集群序列分配给同轨运行的RGV.Gao等[9]构建了在线调度算法,用于调度同轨RGV,以实例证明其可行性.
纵观上述文献,系统中的RGV无论是一辆还是多辆,每次只能搬运单个物品,属于单载量RGV.针对多载量RGV的调度问题,目前仅有Hu等[10]对其作了研究,并考虑了货物装卸顺序约束,应用滚动时域法对RGV作了最优路径规划.
但是,目前尚未发现其他关于同时考虑货物装卸顺序约束和同轨双车避碰调度问题的研究.为此,本文将创新引入 I 类和 II 类冲突的概念,研究多载量RGV货物装卸顺序与同轨双车路径规划相结合的问题,以货物搬运总时间最小为优化目标,建立解除双冲突的决策模型.针对小规模问题,应用CPLEX求其最优解,并构造改进型和声搜索算法获取中大规模的全局满意解.
1 问题描述
如图1所示,AS/RS由两辆RGV(V1,V2)共享同一直线轨道,RGV和货架都安装了滚轮滑道,方便货物的自动存取.系统由RGV按生产计划载运货物至对应货架,以满足生产需求.调度开始前,V1和V2分别位于系统的最左端和最右端,调度开始时,两辆RGV分别从各自的端点启程,完成所分配的任务后,返回至各自的出发点.在此,重点需要解决两个问题:① RGV装卸货物的先后顺序问题,即解决多件货物在RGV内部的死锁问题,此死锁是指已经装载在RGV上的货物,相互阻挡了对方的卸载通道,以致货物被迫处于停滞等待状态;② RGV之间的碰撞问题,即确定避碰情况下的最佳取送路径.
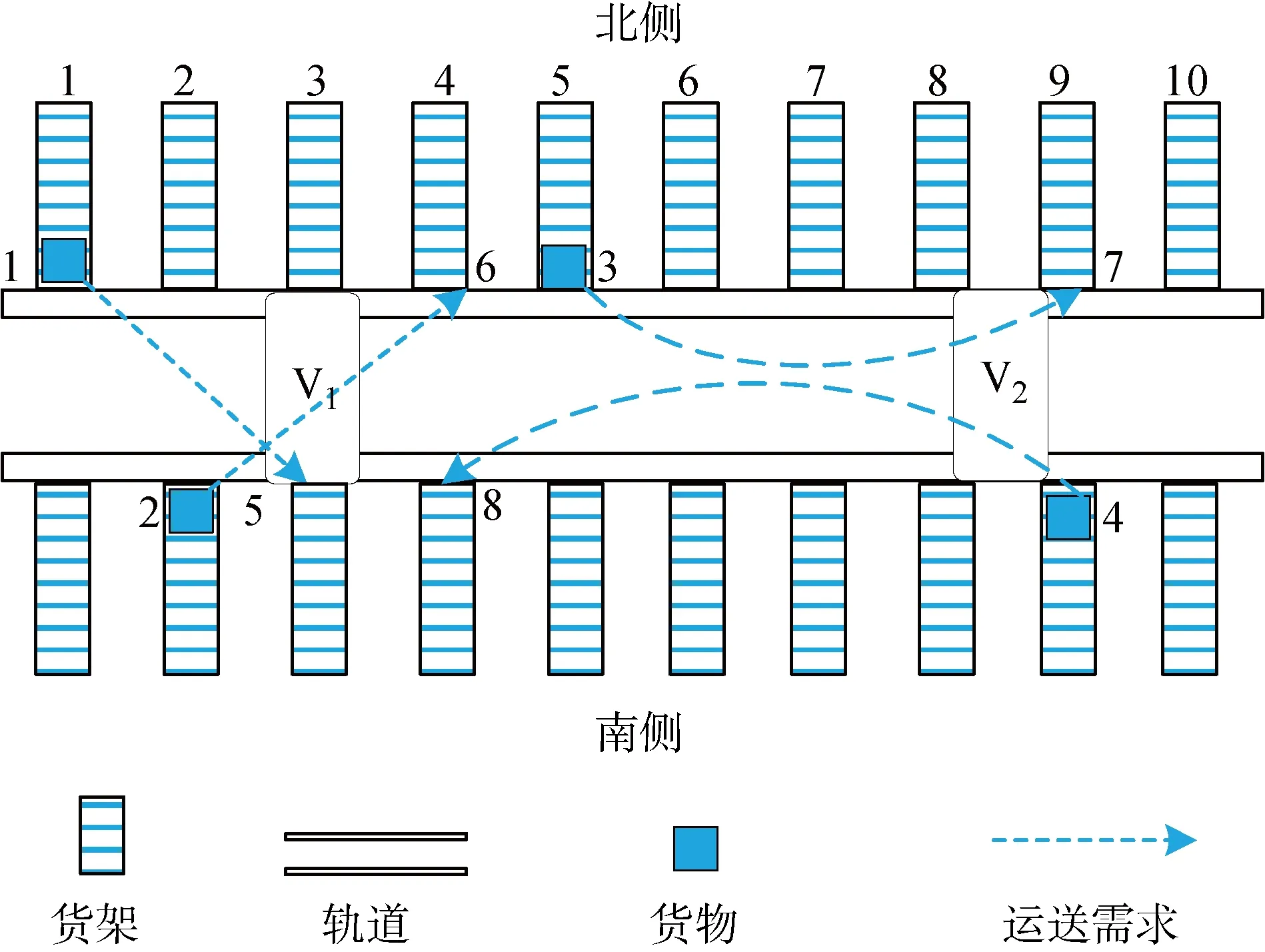
图1 以RGV为存取部件的AS/RSFig.1 Configuration of AS/RS with RGV as storage and retrieval component
为有效描述该存取系统,进行如下基本假设:① RGV可同时搬运多个货物,且车上货物只能顺序装卸;② RGV装载和卸载单位货物的时间相等且为常数;③ RGV不能相互跨越,也不能发生碰撞;④ RGV速度恒定,且两辆RGV型号相同;⑤ 同一轨道位置对应的两对称货架同时只能被一辆RGV访问;⑥ 每个货物的源点和终点已知;⑦ RGV一旦装载了某件货物,到达终点之前,一件货物只能由此辆RGV完成整个搬运过程.



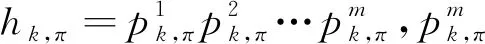
定理1∀t∈T,当Vk同时取送货物组合j∈E3和l∈E4或j∈E4和l∈E3时,发生 I 类冲突.
证明对j∈E3,Vk将rj装载后在车内的移动方向是1→2,若再装载rl,l∈E4,其移动方向为2→1,若将rj,rl形成组合搬运,根据定义1,rj和rl彼此阻碍了对方的目的去向,形成死锁, I 类冲突发生.
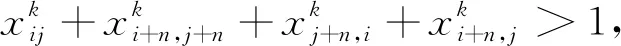


原理与i∈E1,j∈E1/{i}类似,证明略.
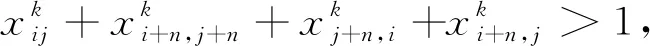
2 数学模型




建立数学模型如下:
minM=
(1)
s.t.
(2)
∀j∈E1/{l},l∈E1,k∈K
∀j∈E2/{l},l∈E2,k∈K
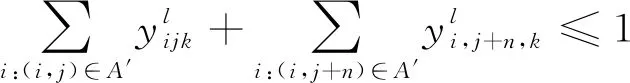
(3)
∀j∈E3/{l},l∈E3,k∈K
∀j∈E4/{l},l∈E4,k∈K
(4)
∀(i,j)∈A′
∀j∈E3/{l},l∈E3,k∈K
∀j∈E4/{l},l∈E4,k∈K
(5)
∀(i,j+n)∈A′
∀j∈E4,l∈E1,k∈K
∀j∈E3,l∈E2,k∈K
(6)
∀(i,j)∈A′
∀j∈E4,l∈E3,k∈K
∀j∈E3,l∈E4,k∈K
(7)

(8)
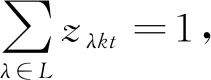
(9)

(10)
z0k0=1,k=1
(11)
z|W|+1k0=1,k=2
(12)
(13)
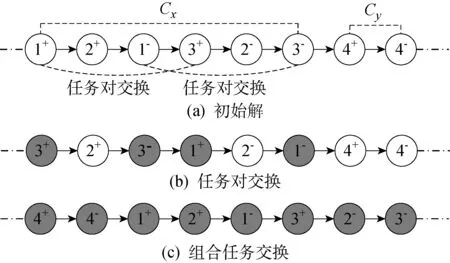
∀i,j∈A,pi (14) (15) (16) (17) (18) (19) zλkt∈{0,1} (20) λ∈{0}∪W∪{2n+1},k∈K 式(1)为Vk在消除两类冲突中最后完成所有任务的最少时间;式(2)~(5)为消除 I 类冲突约束,其中,式(2)为后进先出(LIFO)策略,式(3)为先进先出(FIFO)策略,式(4)为交叉任务先入(CFI)策略,式(5)为交叉任务后出(CLO)策略式;式(6)为 I 类冲突消除;式(7)和(8)表示每个任务只能被服务一次;式(9)~(13)为消除 II 类冲突约束,式(9)~(10)为同一时刻一个位置只能被一辆RGV访问,式(11)~(12)为初始时刻两辆RGV的位置,式(13)表示避免两辆RGV碰撞;式(14)表示每个取货任务必须在对应送货任务之前完成;式(15)表明同一货架有多项任务需要装载,则按照FIFO原则装载,“i⊕1”表示紧接着任务ri的后一个任务;式(16)为Vk的容量约束式;式(17)表示局部取送任务和全局取送任务关系;式(18)~(20)为决策变量的取值范围. 和声搜索算法(HS)最早由Geem等[11]受音乐即兴创作过程的启发而提出,具有原理简单、控制参数少、收敛速度快等优点.然而,该算法仍存在一些缺陷,如搜索后期收敛缓慢、局部搜索能力欠缺、易陷入局部最优,故本文提出改进型和声搜索算法(MHS)求解中大规模问题,以获取较高质量的解.基本步骤如下. 步骤1问题参数初始化.包括和声记忆库大小HMS、最大迭代次数NI、和声记忆库取值概率HMCR、音调微调概率PAR、微调幅度BW以及精度ε. 步骤2和声记忆库初始化.结合式(2)~(6),随机生成HMS个和声向量,存入HM. 步骤3划分和声片段.将每个和声向量按照 I 类约束关系,分解为若干和声片段. 步骤4新和声即兴创作.对于每个和声片段,基于HMCR、PAR进行即兴创作,形成新的和声. 步骤5更新和声记忆库.将新形成的和声和当前最差和声进行对比,若优于当前最差和声,则替代当前和声. 步骤6判断终止准则.若当前迭代次数N大于最大迭代次数NI,则合并所有和声片段形成新的和声记忆库,否则重复步骤 4和5. 步骤7变邻域搜索操作.随机选取一个和声向量进行变邻域搜索操作,并更新HM. 步骤8判断终止准则:若任两个和声对应目标值之差均小于ε,则算法终止,否则重复执行步骤3~7. 用Si(i=1,2,…,HMS)表示和声向量元素,采用3层变长编码方式:第1层表示图G顶点层,代表RGV访问的线路节点;第2层为位置层,代表顶点对应的源点位置p或终点位置d;第3层为执行任务的RGV编号层.以图1为例,若将r1,r2指派给V1,将r3,r4指派给V2,则其中一个可行解可表示为图2.其中顶点层的数字9为2×4+1,位置层中间的“11”表示初始时刻,V2的位置为 |W|+1. 图2 和声编码图解Fig.2 Encoding mode for harmony 给定任务n,根据有向图G的定义以及两辆RGV的起讫点位置,可得和声的最大长度Lmax=2n+4.当n=1时,可知Lmin=5,即一辆RGV的初始点和执行一个完整任务的源点和终点.因此和声Si的长度范围为[Lmin,Lmax]. 编码方案对应的解如图3所示,横线部分表示RGV进行装或卸操作.初始时刻,V1从0位置出发,完成搬运任务后返回至原位置;V2从 |W|+ 1出发,完成分配的任务后返回至出发点.V1对应的路径为0→2→4→1→3→0,执行的任务顺序为②→①;RGV2对应的路径为11→9→4→5→9→11,执行的任务顺序为④→③. 图3 编码方案对应的解Fig.3 Corresponding solution of coding mode 为生产初始可行解,本文采用贪婪随机自适应搜索算法(GRASP)初始化和声记忆库.具体步骤如下. 步骤1随机生成任务矩阵Rn=[r1r2…rn]T,rn=(αn,Pn,βn,Dn),αn=rand(1,2),Pn=rand(1,|W|),βn=rand(1,2),Dn=rand(1,|W|). 如文中提到的山南基金小镇、余杭梦想小镇等对特色小镇产业发展规划进行科学论证,按照主导产业特色鲜明、相关产业按需配套的原则,合理确定特色小镇产业功能布局。一些个别特色小镇用地规模过大,产业定位不够清晰等问题,将不符合土地利用总体规划的建设用地划出规划区范围,在此基础上提出明确的用地需求菜单,落实到城市控规和土地利用总体规划上,科学划分相关功能区块,确定用地类型为特色小镇建设提供科学指引[6]。 (4) 根据定理1及式(2)~(6)判定终点,若终点为di-1,则将di-1设置为新源点,di为新终点,返回(1).若终点为di,则设di为新源点,di-1为新终点,转至(1). 步骤6将h1和h2转化成在[Lmin,Lmax]上的编码,一并存入HM,实现和声记忆库的初始化. 针对每个Sub_HM,新和声Snew以HMCR概率继承现有Sub_HM中和声,并以PAR概率进行微调.同时,对Snew进行邻域搜索,新和声Snew以(1-HMCR)的概率应用GRASP算法进行创作.具体流程如下. r1,r2,r3=rand( ) forj=2 to 2n+2 do ifr1 Snew←Sαwhereα∈(1,2,…,HMS) ifr2 Snew←Snew±r3BW end if else Snew←Sub_HM+GRASP iff(Snew) Sworst←Snew∥*更新HM end if end for 图4 任务对和组合任务的重置操作Fig.4 Re-located operations of couple and component (3) 任务对交换.随机选取两个任务对,交换对应的位置,如图5(b)所示,交换了初始解(图5(a))中r1和r3的位置. (4) 组合任务交换.随机选取两个组合任务,并交换对应的位置,如图5(c)所示,交换了初始解(如图5(a))中Cx和Cy的位置. (5) 变异操作.设原变量Sold经移动操作后得到Smv,若f(Smv) 图5 任务对和组合任务的交换操作Fig.5 Swap operations of couple and component 图6 和声向量变异操作Fig.6 Mutation operation of harmony vecor 重置任务对(ope1)、重置组合任务(ope2)、交换任务对(ope3)和交换组合任务(ope4)4个操作的执行控制为 (21) 式中:q为[0,1]之间的随机数. 经以上操作得到的新向量有可能不可行,为保证解的多样性,允许一定数量不可行解的存在.为此,本文引入罚函数法,通过惩罚函数,所有的不可行解向量都倾向于朝着可行解的方向搜索,从而完成不可行解向可行解的转化. 令 I 类约束式(2)~(6)分别用g1,g2,…,g5表示,II 类约束式(13)用u表示.则罚函数可构建为 (22) 式中:γ>0为违反 I 类约束和 II 类约束的惩罚系数. 基于以上分析,给出MHS的核心流程. 参数初始化:HMS,HMCR,PAR,NI,Sbest 按照GRASP算法,初始化和声记忆库 按rn的数量,规划Sub_HM fori=1 to HMS do iff(Si) Sbest←Si end if end for 新和声创作Snew(见3.3) 更新和声记忆库(见3.4) ifSnew不可行) then end if iff(Snew) Sbest←Snew end if until 达到终止标准 returnSbest 为评价本文提出的MHS算法的有效性,结合文献[10]生成如下参数:Vk(k={1,2})速度v=1 m/s;最大容量Ck=2;装卸时间tu=1 s;货架间距为0.1 m,货架宽为1 m.分别取不同的n和 |W| 的组合,做仿真实验,并进行统计分析. 算法采用MATLAB(R2014a)编程实现,仿真环境是主频为2.60 GHz,内存为16 GB的便携式计算机. 为验证MHS的有效性,将问题规模 |W| 设定为5和10;n设为8、10、12、14、16,且均匀分布于W,进行小规模问题求解.将运行结果与CPLEX12.6进行比较,针对每个 |W| 和n的组合,CPLEX的最大求解时限设为2 h,MHS算法运行10次取其平均值,统计结果如表1所示.其中,最优解是CPLEX求解所得,可以看出,MHS运行得出的结果与最优解的最大偏差为4.68%,小于5%,验证了算法的有效性.另外,“*”表示CPLEX无法在规定的时限内获得最优解,只能获得最优解的下界,因此,有必要构建智能优化算法求解中、大规模的满意解. 令问题规模 |W|∈{15,20},n∈{20,50,80,110}进行中、大规模问题的仿真,以验证MHS的有效性.由于本文研究的问题没有标准的算例库,考虑到本调度问题与同时取送(SPD)问题有一定的相似性,而文献[13]的混合遗传算法(HGA)和文献[14]的粒子群算法(PSO)在求解取送问题(PDP)上具有较好性能,故将其用于本文的中、大规模问题求解.为了让文献的算法更好地求解该问题,初始种群同样由GRASP算法产生,编码方案做了细微的修改,并加入了3.4节的变邻域搜索操作,以彰显与目标算法(MHS)的可比性.表2所示为将MHS获得的结果和HGA、PSO 得到的结果进行了对比统计.从表中可以看出:随着问题的扩大,MHS的寻优能力明显比HGA和PSO突出;当n=110时,最大相对偏差达到11.02%和9.92%,一定程度上验证了MHS求解中、大规模问题的有效性. 表1 小规模问题实验结果Tab.1 Results of small scale instances 表2 MHS、HGA和PSO的实验结果统计Tab.2 Experimental results of MHS, HGA and PSO 为进一步验证MHS的收敛性能,令问题规模 |W|=15,n=50以及 |W|=20,n=110,绘制两种组合的收敛曲线,将其与HS常见的两种改进型算法,即改进型和声搜索算法(IHS)和全局最优和声搜索算法(GHS)进行对比,结果如图7所示. 由图7可见,3条曲线的收敛趋势大抵一致,主要原因在于都是在基本HS的基础上对其后期收敛速度慢进行改进.中小规模下,3种算法都能在较短时间内搜索到最优解,随着规模的增大,本文融入的变邻域搜索机制使得MHS能够在搜索深度上更胜一筹,如图7(b)所示.实验结果表明,MHS具备良好的收敛性能. 为评估本文调度方法对系统效率的影响情况,引入AHT和ART两个参数作为衡量基准.AHT表示任务的平均搬运时间,其值越小,表示系统的运行效率越高;ART表示为了避免 II 类冲突,RGV之间相互避让,导致货物在车上的滞留时间,其值越小,说明调度越有效. 令 |W| 分别为6,8,10,12,14,16,18,20,任务n=50,仿真实验结果如图8所示,其中,t′为任务所需平均时间. 由图8可见:当 |W| 从6增加到16时,AHT呈逐渐下降的趋势,主要原因可能是空间狭窄,任务都集中在较少的货架上,两辆RGV相互干扰,大部分的时间花费在等待上;而 |W|>16时,AHT开始逐渐增加,空间问题逐步得到缓解,两辆RGV基本可以按照各自的预定线路进行搬运;ART则是逐渐下降,当 |W| 从6增加到16时下降缓慢;当 |W|>16时,其值下降趋势明显;同AHT变化的原因一致,RGV之间的干扰降低,货物的滞留时间也随之减少,货物在小车上的滞留时间几乎等于货物的搬运时间.从上述结果来看,两辆RGV同时作业,货架数量 |W|>16比较合适.当货架数量比较少(少于16)时,不太适合采用多RGV同时作业. 本文研究了自动存取系统多载量RGV避碰调度问题,在对问题描述的基础上建立了混合整数规划模型.在算法部分,提出改进型和声搜索算法,在局部搜索部分融入了变邻域搜索机制,以提高基本和声搜索算法后期的收敛速度和解的质量.同时,引入AHT和ART两个参数作为系统搬运效率的评价指标,当货架数量大于16时平均搬运时间呈缓慢递增趋势,货物在RGV内的平均滞留时间呈持续下降趋势,说明了调度的有效性.3 改进型和声搜索算法
3.1 和声编码方案


3.2 和声记忆库初始化



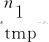



3.3 即兴创作产生新和声

3.4 变邻域搜索操作






3.5 MHS的核心流程


4 仿真实验及分析
4.1 算法有效性验证
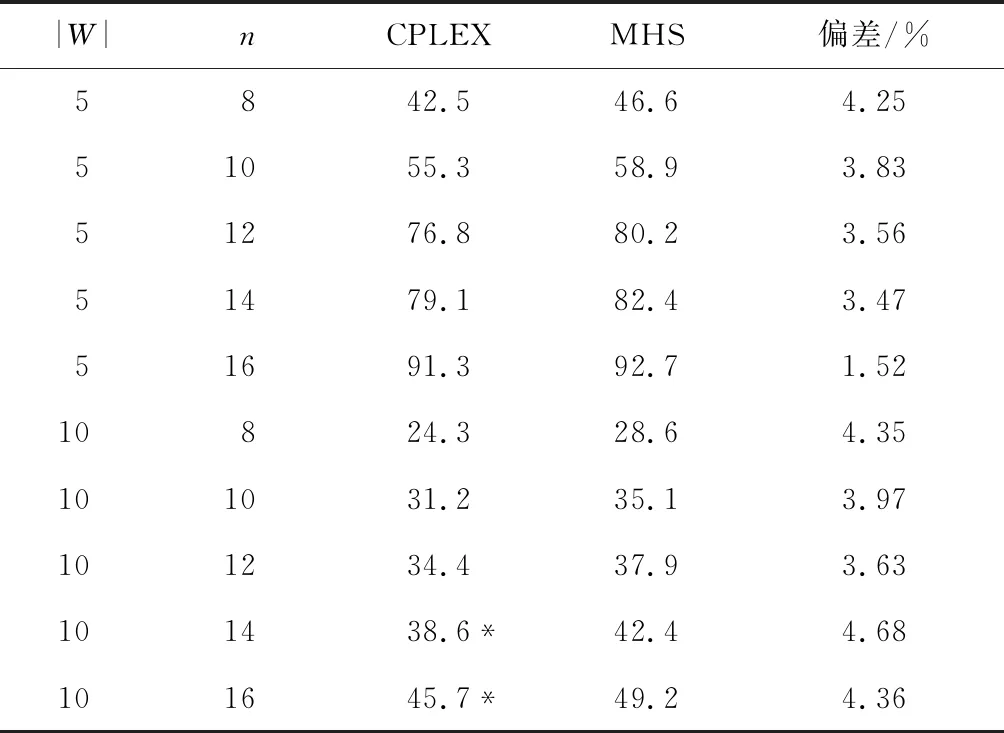

4.2 MHS收敛性验证
4.3 系统搬运效率分析
5 结语
