叶片摩擦系数对液压凸轮转子伺服马达转矩性能影响
2020-03-09陶建峰陈良深王旭永
谭 顿, 陶建峰, 陈良深, 王旭永
(上海交通大学 机械与动力工程学院, 上海 200240)
凸轮转子叶片马达具有体积小、结构工艺简单、输出转矩小、瞬时流量脉动小、工作寿命长、转动惯量小以及动作灵敏等特点,在全液压三轴无磁转台等领域凸轮转子叶片马达得到了广泛应用[1-4].
文献[5]建立了凸轮转子叶片马达阻力矩的数学模型,为马达在控制策略上的摩擦补偿等措施提供了一定的参考.文献[6]研究了叶片端面对叶片与凸轮转子之间正压力和阻力矩的影响.文献[7]讨论了凸轮转子叶片马达干扰力矩与过渡曲线中心角的关系.文献[8]证明了干扰力矩是基于凸轮转子叶片马达工作原理的脉动转矩,可减小叶片厚度以及减压油路压力,从而减小干扰转矩.在保证加工以及润滑良好的情况下,叶片与凸轮转子之间正压力和摩擦力是马达低速特性的决定性因素[9].叶片与叶片槽之间的摩擦系数会影响凸轮转子施加于叶片的正压力以及叶片施加于凸轮转子的阻力矩,从而影响马达转矩特性.
目前,对于马达转矩特性的研究大多集中在马达结构设计方面,例如设计不同的叶片端面、叶片厚度和过渡曲线中心角.此外,已有的研究对凸轮转子叶片马达干扰力矩的数学模型进行仿真时,马达叶片与叶片槽之间的摩擦系数被设置为定值,忽略摩擦系数对马达转矩特性的影响.本文建立了基于凸轮转子连续回转电液伺服叶片马达的转矩力学模型,推导了凸轮转子阻力矩与叶片和叶片槽之间摩擦系数的关系式,并进行了仿真与实验.本研究可为马达叶片材料的选择提供一定的理论依据.
1 凸轮转子叶片马达结构原理
凸轮转子叶片马达的结构如图1所示.互相垂直的左、右凸轮转子与主轴通过键联接,凸轮转子长径和定子内孔系滑动配合.凸轮转子将作用在凸轮外表面的高压油产生的驱动力矩传递至主轴,从而驱动连接至主轴的负载.

图1 凸轮转子叶片马达的结构原理图Fig.1 Structural schematic diagram of cam-rotor vane motor
马达腔内两个定子和两个凸轮转子被定子之间的隔板隔开,形成封闭腔.凸轮转子马达运转时,叶片在定子上的叶片槽内径向运动.叶片根部的减压油对叶片施加压力,使叶片与凸轮转子保持贴合.因此叶片隔离了吸、压油腔.凸轮转子每转一圈就完成吸压油各两次.两个凸轮在空间上呈90°,使得马达在 360° 内始终等效作用有1个恒值驱动力矩,该力矩由凸轮转子在吸、压油腔压差作用下产生.若凸轮转子施加于叶片的正压力过小,将会影响到凸轮转子与叶片的紧密贴合,甚至造成两者脱离,引起马达故障.若叶片施加于凸轮转子的阻力矩相对于对马达输出力矩的影响已经不能忽略,将造成马达输出力矩波动明显,严重影响马达的低速特性.
2 叶片受力分析
2.1 凸轮转子过渡曲线
凸轮转子的轮廓如图2所示.图中,叶片11与叶片12为左凸轮上的一对叶片;叶片21与叶片22为右凸轮上的一对凸轮;φ为凸轮转子转角;ω为凸轮转子角速度;R和r分别为大、小圆弧的半径;ρ1和ρ2分别为叶片11、21处的凸轮曲率半径.两段大圆弧和两段小圆弧以及4个过渡曲线组成了凸轮转子的轮廓曲线.大圆弧和小圆弧所对应的中心角相等,记为β.过渡曲线的中心角相等,记为α,满足α+β=90°.为了简化分析过程,将两个凸轮转子上的两对叶片及其相对位置叠加在一个凸轮转子上.
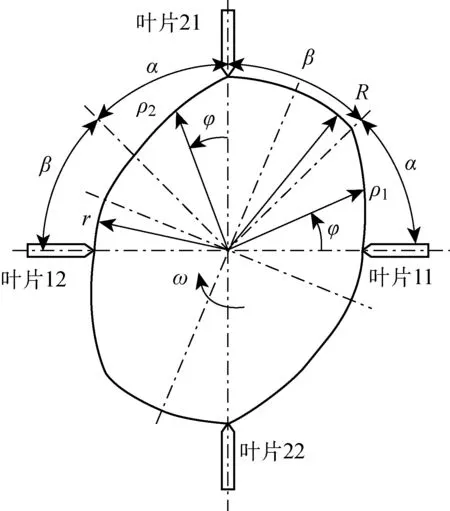
图2 凸轮转子轮廓示意图Fig.2 Outline of the cam-rator
本文中凸轮转子过渡曲线选用二次余弦曲线:
(1)
0≤φ≤α
2.2 叶片受力分析
叶片运动时的加速度不大,且其质量较轻,因此惯性力可以忽略.设定马达顺时针旋转.当叶片处于凸轮转子圆弧段时受力情况比较简单,本文仅对叶片处于过渡曲线段(0≤φ≤α)的受力情况进行分析.
当叶片处于过渡曲线段时,其受力情况如图3所示.图中Fi1和Fi8分别为叶片上、下端面所受的压力(i=1代表左凸轮,i=2代表右凸轮,下同);Fi3和Fi4为叶片槽表面对叶片的正压力;Fi2和Fi5为叶片槽表面对叶片产生的摩擦力;Fi6和Fi7分别为凸轮转子对叶片的摩擦力和正压力;Fi9为叶片处于油腔段侧面所受液压力;γ1和γ2分别为左、右凸轮上的压力角.
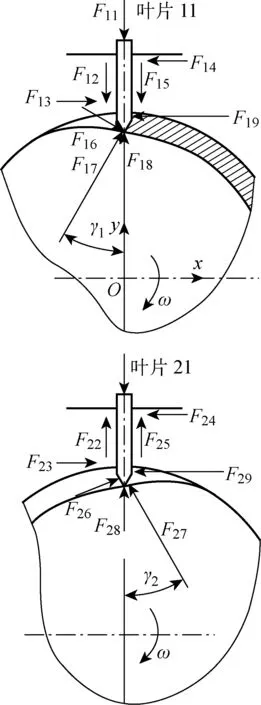
图3 叶片受力分析示意图Fig.3 Schematic diagram of force analysis of the vane
由图3可知:
式中:s为叶片厚度;b为叶片宽度;pa、pb以及pc分别为进油口油压、减压阀出口油压以及回油口油压.
首先对左凸轮进行分析,建立图中所示的直角坐标系,由受力平衡条件可以得到x方向上力的平衡条件为
F14+F19=F13+F16cosγ1+F17sinγ1
(5)
y方向上力的平衡条件为
F11+F12+F15+F16sinγ1=F18+F17cosγ1
(6)
以叶片和凸轮之间的接触点作为中心点建立转矩平衡方程:
(7)
式中:h为叶片槽长度.联立式(2)~(7)可得:
F17=[F19(R+h-ρ1)f+h(F11-F18)]/
[(2fcosγ1+2sinγ1)(R-ρ1)f+
h(f2+1)cosγ1]
(8)
式中:f为材料摩擦系数.
对右凸轮进行类似的分析,同理可得:
F27=[F29(R+h-ρ2)f-h(F21-F28)]/
[(2fcosγ2-2sinγ2)(R-ρ2)f+
h(f2cosγ2-cosγ2-2fsinγ2)]
(9)
叶片对凸轮转子的阻力矩主要来自正压力和摩擦力,左、右凸轮转子对叶片的正压力产生的阻力矩分别为
摩擦力产生的阻力矩分别为
M12=-fF17ρ1cosγ1
(12)
M22=-fF27ρ2cosγ2
(13)
由于每个凸轮有两个叶片,所以叶片对凸轮转子的总干扰阻力矩为
Ms=2(M11+M12+M21+M22)
(14)
联立式(10)~(14)可以得到:
Ms=2F17r1(sinγ1-fcosγ1)-
2F27r2(sinγ2+fcosγ2)
(15)
3 仿真与结果分析
马达的相关参数为:R=45 mm,r=39 mm,s=3 mm,b=25 mm,h=15 mm,油源压力ps=5 MPa,并设定pa=5 MPa,pc=0.
改变材料的摩擦系数的值,利用第2节中的叶片受力分析结果,通过MATLAB仿真得到不同f下叶片受到凸轮转子的正压力和凸轮转子受到叶片的阻力矩的变化情况分别如下:
(1)f对叶片所受正压力的影响(取pb=5 MPa)
图4为不同f条件下凸轮转子对叶片正压力的变化曲线图.可以看出,叶片处于不同的曲线段时,f对正压力的影响情况不同.当φ为0°~45° 时,随着f的增大,凸轮转子对叶片的正压力不断增大;当φ为45°~90° 和135°~180° 时,f对正压力影响比较小;当φ为 90°~135° 时,随着f的增大,凸轮转子对叶片的正压力不断减小.

图4 不同f条件下凸轮转子对叶片正压力变化Fig.4 Positive pressure curve of cam-rotor applied to vane under different friction coefficients

图5 F17的平均值和最小值与f关系曲线Fig.5 The relationship between the average value and minimum value of F17 and friction coefficient
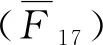
(2)f对阻力矩的影响(取pb=5 MPa)
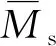

图6 不同f时叶片对凸轮转子总阻力矩变化Fig.6 The variation of resistance torque applied by vane to the cam-rotor under different friction coefficients

图7 马达理论转矩和合成转矩比较(f=0.1)Fig.7 Comparison of motor theoretical torque and combined torque (f=0.1)
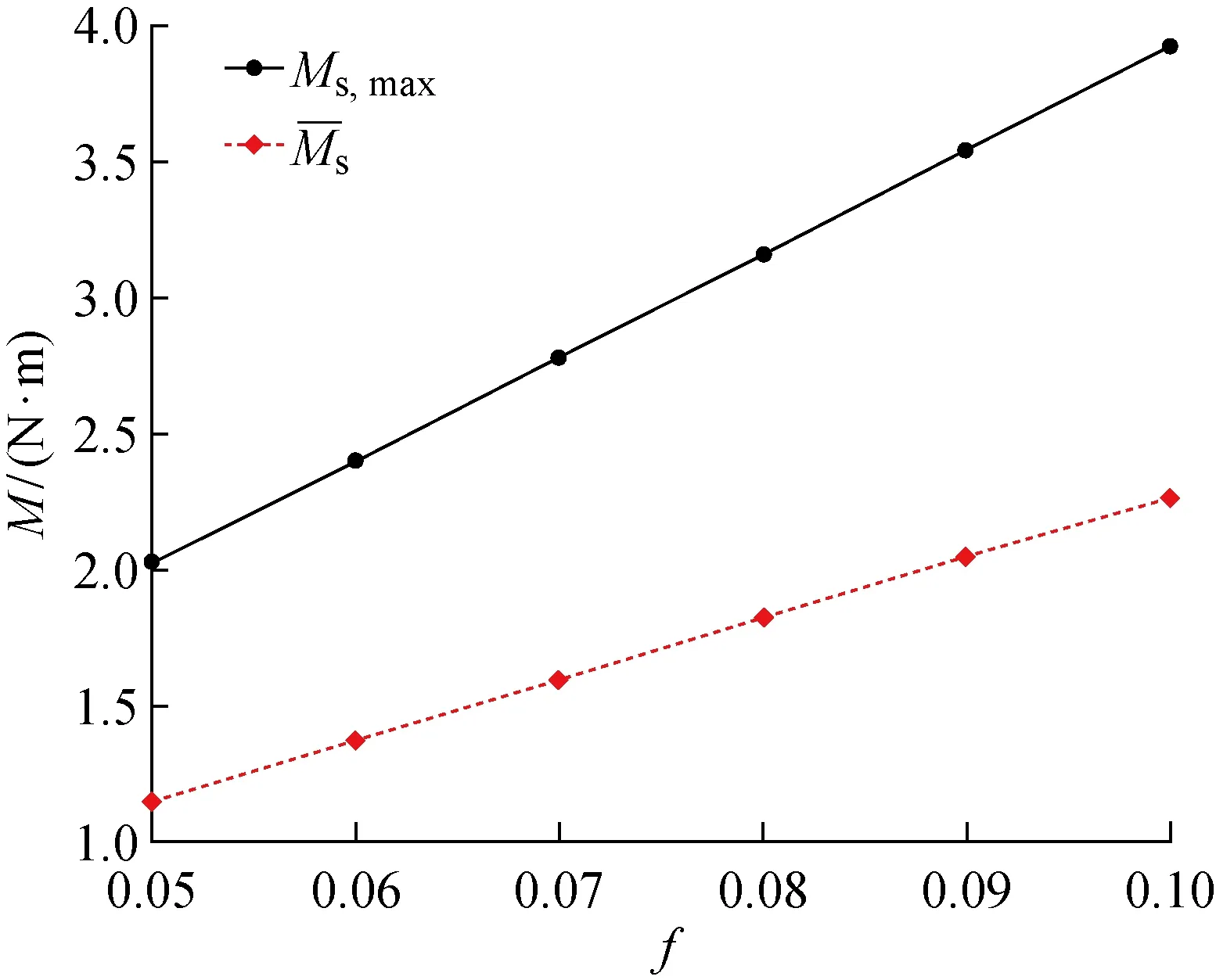
图8 Ms,max和与f关系曲线Fig.8 The relationship between Ms,max, and f
因此,在加工条件允许的情况下,应该尽量提高叶片和叶片槽的形位公差和表面粗糙度,减小其材料摩擦系数,从而达到改善伺服马达性能的目的.
4 试验结果
基于上述马达叶片摩擦系数对马达阻力矩的分析,本文对试制的凸轮转子液压伺服马达的叶片和叶片槽加工质量进行了有针对性的控制,并进行了该马达的低速实验测试.凸轮转子马达驱动负载,用22位光栅编码器作角位置反馈传感器.马达实验系统的外观和马达叶片的侧面分别见图9和10.

图9 带负载的凸轮转子马达伺服系统Fig.9 Cam-rotor motor servo system with load

图10 叶片和叶片槽实物图Fig.10 Physical picture of vanes and vane slots
对马达叶片和叶片槽进行配合研磨以降低摩擦系数.马达伺服控制系统的采样频率为1 kHz.输入信号为0.001 °/s的低速斜坡信号,得到马达叶片和叶片槽配合研磨之前、之后马达实时位置跟随曲线,如图11及12所示.
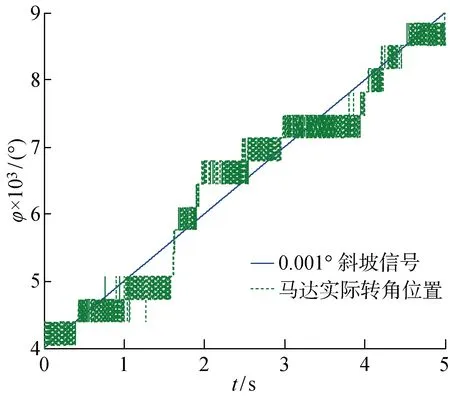
图11 研磨前输入为0.001°/s的斜坡信号时系统响应曲线Fig.11 Response curve of the system when the input is a ramp signal of 0.001°/s before being ground

图12 研磨后输入为0.001°/s的斜坡信号时系统响应曲线Fig.12 Response curve of the system when the input is a ramp signal of 0.001°/s after being ground
实验表明,经过叶片和叶片槽研磨后的凸轮转子伺服马达低速性能有所改善.图13和14分别为对马达叶片和叶片槽进行配合研磨之前、之后马达低速跟随时的角位置误差(E).图13中位置误差在±0.001°.图14中位置误差控制在 ±0.000 5°.这表明,经过叶片和叶片槽精磨后的凸轮转子伺服马达阻力矩波动较小,马达输出力矩波动也较小,有助于改善马达的低速性能.

图13 研磨前输入为0.001°/s的斜坡信号时系统跟踪误差曲线Fig.13 System tracking error curve when the input is a ramp signal of 0.001°/s before being ground
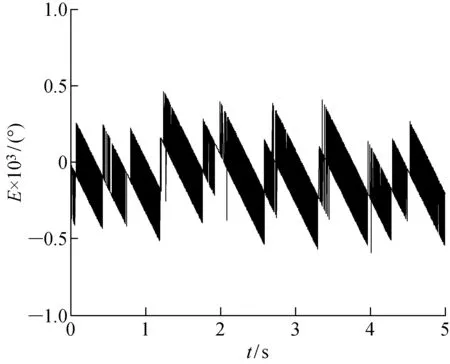
图14 研磨后输入为0.001°/s的斜坡信号时系统跟踪误差曲线Fig.14 System tracking error curve when the input is a ramp signal of 0.001°/s after being ground
5 结论
(1) 材料摩擦系数会影响凸轮转子和叶片之间的正压力.当叶片处于凸轮转子的不同位置时,材料摩擦系数对其影响程度不同.随着材料摩擦系数的增大,凸轮转子和叶片之间正压力的最小值不断减小.当材料摩擦系数达到一定数值,凸轮转角为 90°~135° 时,正压力最小值出现负值,马达高压腔和低压腔串通,马达因吸、压油腔无法建立起压差而丧失驱动能力.
(2) 随着材料摩擦系数增大,叶片对凸轮转子的阻力矩的平均值和最大值均增大,导致马达输出力矩出现明显波动.摩擦系数的增大不利于马达低速性能的改善.
(3) 仿真计算表明,叶片与叶片槽之间的摩擦系数与凸轮转子马达阻力矩基本呈线性正相关.
(4) 实验结果表明,对叶片和叶片槽采取研磨等措施降低摩擦阻力,有利于改善对马达的低速性能.
