双向部分透明供应链的大数据投资决策与激励
2020-03-09周茂森张庆宇
周茂森,张庆宇
(1.深圳大学管理学院,广州 深圳 518060;2.深圳大学商业分析与供应链研究所,广州 深圳 518060)
1 引言
互联网、物联网和智能技术的发展加剧了供应链环境的复杂性和不确定性,而大数据的开发和应用有利于企业更好地感知和应对环境的变化[1]。然而,大数据开发需要在数据采集、存储和处理等方面持续投入高成本的硬件、软件和人力,会给企业造成巨大的财务预算压力[2]。并且,Mc Kinsey 的调查表明,企业已耗费大量的大数据投资,但对这些投资的回报却不得而知,事实上,这些投资在过去几年中对收益和成本的改进只是微乎其微[3]。由此表明,高投入和不明朗的投资回报是制约大数据可持续开发的瓶颈问题。另一方面,在供应链中,传统需求预测较多依赖于下游企业通过POS系统、销售服务、市场调查等方式采集预测数据,然而现今,上游企业也能利用大数据技术采集预测数据,例如,美的公司投资构建“开普勒数据云”采集和分析1.67亿用户数据,使制造效率提升15%。并且,上下游企业同时采集预测数据也较为普遍,如宝洁公司(P&G)与沃尔玛(Walmart)、麦德龙(Metro)、特易购(Tesco)等下游企业彼此交换数据并实现协同需求预测[4]。可见,供应链上下游企业均可通过大数据投资预测市场需求。当前,信息共享是缓解大数据投资压力的重要途径,已有大量文献论证了其战略作用和价值[5]。然而,随着数据资源在容量、维度和更新速度上的爆发式增长,要实现信息共享不仅要解决企业的策略性共享动机问题,还要在实施中面对难以逾越的技术障碍,如不同企业信息系统难以兼容、数据传输和同步能力有限、共享平台构建受到预算约束等[6]。这又表明,大数据的投资分散与难以完全共享已是不可忽视的现实。鉴于此,如何衡量大数据价值与投资回报、供应链的不完全透明如何影响大数据投资决策、分散的大数据投资存在怎样的相互作用、如何解决潜在的大数据投资激励失调问题等,是促进大数据在供应链中的可持续开发和应用有待解决的重要问题。
目前,尚未发现直接针对供应链中大数据投资问题的理论研究,而本文与供应链管理领域涉及上下游纵向透明与信息获取两方面的研究相关。一方面,较多文献考虑信息获取行为外生,研究纵向透明的价值与信息共享激励问题,常见于四种供应链类型。第一种是双边垄断的供应链,如Chu等[7]研究制造商同时决策产能和批发价格对于信息共享的激励作用,卢继周等[8]研究供应链透明对于牛鞭效应的抑制作用;第二种是上游垄断而下游竞争的供应链,如Shamir[9]考察下游零售商可能同时存在纵向信息共享与横向信息共享情形,戴宾等[10]考察制造商向零售商共享生产成本信息的三种策略对竞争环境的适应性;第三种是两条双边垄断的竞争性供应链,如Shamir和Shin[11]研究下游零售商向制造商和竞争对手同时公开需求信息对所有企业和消费者利益的影响,Ha等[12]研究各条供应链中的制造商存在成本节约努力时下游零售商的纵向信息共享激励问题。第四种是上游竞争而下游垄断的供应链,如Shang等[13]考察非线性制造成本下零售商向上游制造商共享需求信息的激励问题,罗春林等[14]考察制造商的制造成本结构和信息精度如何影响销售平台的信息共享激励。上述文献考虑单向透明情形,也有少量文献考虑上下游存在双向透明的情形,如Bian等[15]考虑上下游企业的私有信息存在双向完全透明和完全不透明两种情形。然而,现有文献大多考虑完全透明和不透明两种离散情形,且尚未研究双向且部分透明的情形。
另一方面,也有文献考虑信息获取行为内生,研究供应链中的信息获取价值与决策问题,主要文献可分为三类。第一类文献考察纵向完全透明时下游企业的单边信息获取问题。例如,Taylor 和Xiao[16]针对双边垄断的供应链,基于固定的信息获取成本对比考察销售返点和剩余补偿契约对下游零售商信息获取行为的激励作用;Fu Qi和Zhu Kaijie[17]针对双边垄断的供应链,考虑线性的信息获取成本,综合考察数量折扣、数量柔性、回购和收益共享等不同契约对下游零售商信息获取行为的协调能力;Shin和Tunca[18]针对上游垄断而下游竞争的供应链,考虑凸性信息获取成本,为下游零售商的信息投资提供基于市场价值指数契约协调方案;肖群和马士华[19-20]进一步研究零售商的风险厌恶对其信息获取投资的影响,并先后基于收益共享、预测成本分担和回购等机制提出契约协调方案。第二类文献通过比较完全透明和完全不透明两种情形,考察纵向完全透明对单边信息获取行为的影响。例如,Guo Liang[21]考虑两种常数状态的信息获取成本,研究批发价格契约下的信息投资与共享对供应链绩效的影响;Chen Fangruo等[22]考虑凸性信息获取成本,研究同时协调下游销售商信息投资和销售努力的契约方案;Huang Song和Yang Jun[23]研究零售商如何通过契约机制应对上游供应商的生产成本信息获取与信息质量披露行为;Guan Xu 和Chen Yingju[24]研究下游零售商存在理性推断时制造商的产品质量信息获取与披露行为的交互影响;Tang和Girotra[25]研究批发商如何采用提前采购折扣契约激励零售商的需求信息获取与共享行为。此类研究近期较活跃,但尚未考察供应链中存在部分透明的影响。第三类文献考察上下游企业均存在的双边信息获取行为,此类文献并不多见,主要包括:Zhu等[26]研究制造商和零售商均存在线性信息获取成本时纵向透明对于各参与者信息获取激励的影响;Kurtulus 等[4]认 为 有 关 协 同 预 测 (collaborative forecasting)的研究大多假定信息精度外生,且忽视信息获取行为之间的交互作用,因而考虑上下游企业同时存在信息获取决策,对协同预测的价值与激励问题展开新的研究;进而,Galbreth 等[27]的研究还发现协同预测可能降低需求预测精度。现有文献尚未考察供应链的部分透明或双向透明对信息获取行为的影响,而针对双边均存在信息获取行为的研究也较为缺乏。
本文基于现有研究,将针对单个供应商和制造商组成的供应链,考虑上下游企业间可能存在“自下而上、自上而下”的双向部分透明,并且均能通过大数据投资获取需求预测信息,基于理论分析模型揭示大数据的增值路径和投资激励失调问题,并提出契约解决方案。与现有研究的区别在于:(1)考虑上下游企业均能获取需求信息,能够反映供应链中大数据存在分散投资的现实,并采用一般性的投资成本函数,提高研究结论对不同成本函数的普适性;(2)允许供应链中存在部分透明,实现对“完全透明、完全不透明”两种情形的连续化处理,不仅能应对供应链中普遍存在的部分透明问题,还能提高研究结论的可靠性;(3)允许供应链中存在双向透明,可适用于上下游企业间存在大数据交换的情形,也能揭示双向透明的交互影响。本文工作虽不足以完全揭示和解决大数据的可持续开发与应用问题,但可从战略分析视角为供应链中大数据的研究与实践提供可以借鉴的理论和方法。
2 问题和模型描述
需求不确定环境下,由一个部件供应商(s)和一个产品制造商(m)组成的供应链系统。考虑单个产品销售周期,在销售季来临前,制造商向供应商采购部件并完成产品生产;在销售季来临时,制造商按出清价格销售产品,其逆需求函数可表达为:

其中:q为产品数量;a+ε为顾客最大支付意愿,ε是均值为0和标准差为σ的随机变量,表示不确定性因素的影响,a≫σ。供应商和制造商的边际成本为常数cs和c m。模型主要构成与假设如下。
2.1 大数据投资
面对不确定需求,各参与者(i=s,m)均可通过投资获取需求大数据的采集和分析能力,增强需求预测的及时和准确性,从而提升其运营决策对需求变化的敏捷性。因此,考虑各参与者i在大数据投资后,能够在销售季来临前及时观测市场变化、采集并分析多源、海量数据,最终形成规模为ni的标准化数据集合,设为 (ri1,…,rin),满足rik=ε+uik,∀uik∈ {uik|i=1,2;k=1,…,n}。假设数据噪音uik服从均值为0、标准差为σu的独立同分布,且与ε独立。用均值表示各参与者i的观测信息,满足E[Y i|ε]=ε,且Y1和Y2服从ε条件下的独立分布。考虑真实需求不能被完美观测,故设E[Var(Y i|ε)]>0。将Yi的信息精度定义为ti=Var(ε)/E[Var(Y i|ε)]。由E[Var[Yi|ε]]=/ni可知,ni越大或σu越小,则ti越大。
一般地,大数据投资越大,对需求大数据的采集(增大ni)和分析(减小σu)能力越强。因此,用信息精度ti表征大数据投资水平。考虑各参与者的大数据投资均取决于大数据技术的社会发展水平,成本结构相同。并且,在不同应用场景,大数据投资可能存在不同成本结构,如各种线性或非线性的成本函数。不失一般性,类似文献[17],将投资成本结构用二阶可微凸函数I(ti)表示,满足I″(ti)≥0,I′(ti)>0和I(0)=0。
大数据技术发展水平越高,进一步提升大数据能力的投资压力越小,也就是说,大数据开发的边际成本取决于大数据技术水平。因此,可用I′(ti)表征大数据技术水平,I′(ti)越小,表示大数据技术水平越高。此外,考虑大数据投资相关信息可公开获取,如通过新闻公告、财务报告、项目信息等,故假定各参与者确定的投资水平为共同知识。
2.2 供应链透明与信息结构
考虑各参与者的大数据为私有信息,但彼此可进行交换,因而供应链中大数据存在两种纵向共享方式:一种是上游供应商向下游制造商共享,即自上而下的正向大数据共享;另一种是下游制造商向上游供应商共享,即自下而上的逆向大数据共享。大数据共享能促进私有信息在供应链中的透明化,从而改变各参与者的信息状态。为明确大数据共享与供应链透明度的关系,给出如下定义。
定义1对于由上下游两个参与者 (i=s,m)组成的供应链,考虑各参与者i从其规模为n i的私有数据集中随机抽取n′i份数据与另一参与者共享。此时,可将λi=n′i/ni定义为参与者i的大数据共享水平,满足0≤λi≤1,并用(λs,λm)表示供应链在正向和逆向的双向透明度。
依据定义1,当 (λs,λm)= (0,0)时,表示双向完全不透明,当 (λs,λm)= (1,1)时,表示双向完全透明,而其它情形,则表示双向部分透明。并且,不同的双向透明度会对各参与者的信息状态存在不同影响。将各参与者的原始观测信息重新表达为:
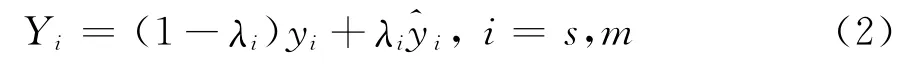
其中:y i和分别表示参与者i保留和共享的观测信息。借鉴Li[28]的研究,在透明度(λs,λm)的影响下,参与者i的信息状态可表示为:
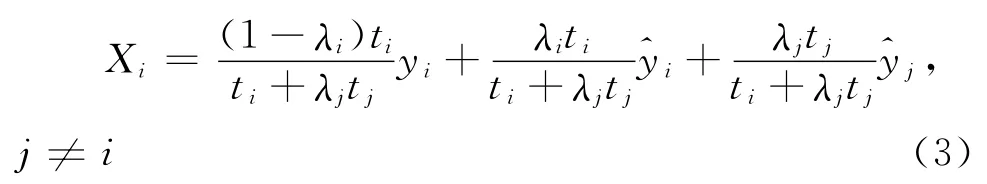
在需求预测方面,类似较多相关研究,如文献[10-14],采用线性的贝叶斯推断模型。因此,由统计学原理可得如下信息结构:

2.3 事件顺序
跨企业数据共享可能受技术、法律等多种因素限制,且技术平台构建复杂,短期内不易改变,而数据也可能由非官方途径间接扩散,未必按照企业意愿。因此,将供应链透明度(λs,λm)视为影响大数据投资决策的外生环境因素。大数据共享决策虽不属本文研究范畴,但也可基于本研究进一步探索其均衡与激励问题。如图1,事件与决策顺序如下:
(1)依据长期给定的供应链透明度(λs,λm),供应商和制造商同时决策大数据投资水平ts和t m。
(2)依据投资开发的大数据能力,各参与者通过观测获取需求大数据,并且,在既定的供应链透明度下,供应商和制造商实现大数据交换,信息状态更新为X s和X m。
(4)依据大数据Xs,供应商确定批发价格w。
(5)依据大数据X m和w,制造商确定产量q,并向供应商采购等量部件完成产品生产。
(6)实际需求发生,制造商以价格p销售产品,供应商和制造商分别实现利润πs和πm。其中:

可以看到,大数据投资绩效受两阶段影响:首先是大数据开发阶段,即各参与者在需求观测前同时决策大数据投资水平;其次是大数据应用阶段,即各参与者在需求观测后利用大数据分别决策批发价格和产品数量。因此,大数据的价值创造取决于其投资水平及其对生产运营决策的影响。
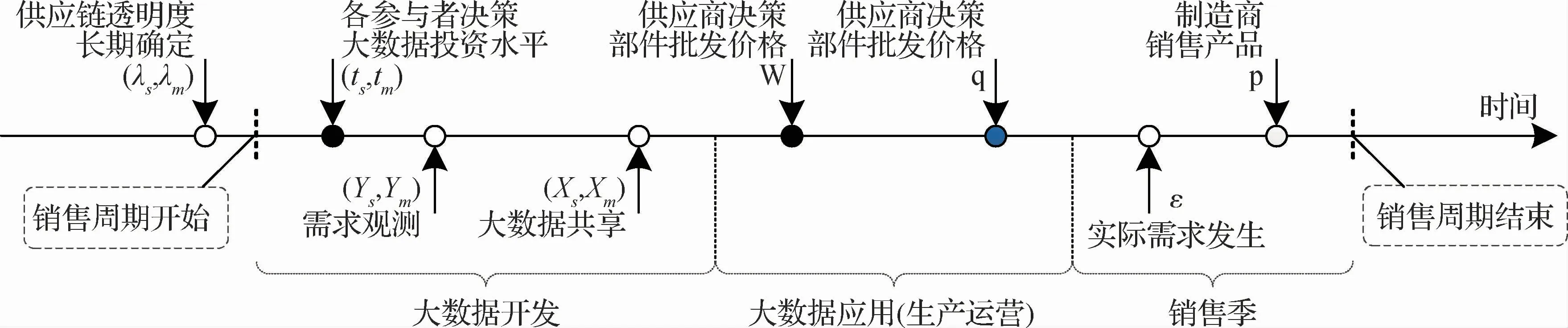
图1 事件时序图
3 大数据应用阶段
在大数据驱动下,生产运营决策能更好适应需求变化,从而获取敏捷性绩效。大数据的投资激励取决于其对敏捷性绩效的影响。采用逆向归纳法,先分析大数据应用阶段的生产运营决策,进而在下节研究大数据开发阶段的投资决策与激励问题。
3.1 生产运营决策
大数据应用阶段的均衡问题为:
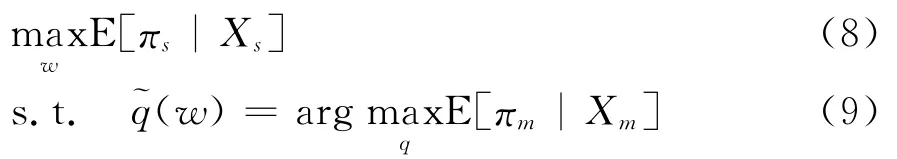
求解(9)式可得制造商关于q的最优反应函数:
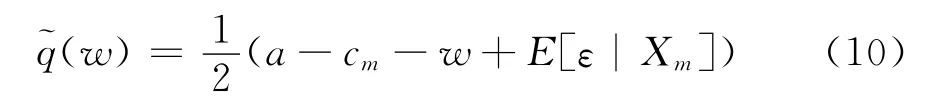
再将(10)代入(8),由一阶条件可得均衡解w。
定理1在大数据应用阶段,存在唯一的子博弈精炼均衡,且各参与者均衡策略分别为:

依据定理1,制造商和供应商的大数据分别通过E[ε|X m]和E[E[ε|X m]|Xs]影响均衡决策,为便于阐释大数据对生产运营决策与绩效的作用路径,本文提出大数据的两种效应。一种是用E[ε|X m]表征的预测效应,对产量具有正影响,表示制造商依靠大数据预测能更好地捕捉市场需求变化,从而提高产量决策对需求变化的适应能力,即提高产量敏捷性。该效应取决于市场需求的不确定性和制造商的大数据预测行为,需求波动越大、制造商的大数据越充足,该效应越显著。
另一种是用E[E[ε|Xm]|Xs]表征的策略效应,对批发价格和产量分别有正影响和负影响。在分散式供应链中,各成员均为边际利润的追逐者,供应商会利用批发价格策略攫取制造商的边际利润,从而形成“双重边际效应”,对制造商产量造成负面影响,见(10)式。在需求不确定时,制造商利用大数据能更好预测需求变化,提高产量敏捷性,从而增加边际利润。鉴于此,供应商为进一步攫取制造商新增的边际利润,也会利用大数据更好地预期制造商的产量反应趋势,从而提高批发价格策略对产量趋势的适应能力,即提高批发价格的敏捷性。由此可见,供应商的大数据能通过提高批发价格敏捷性进一步攫取制造商的边际利润,即加剧双重边际效应,最终对产量造成更大的负面影响,即抑制产量的敏捷性。因此,该效应的根源为供应商攫取制造商边际利润的策略性行为,同时取决于需求不确定性、上下游的大数据预测行为。并且,预测效应是策略效应的存在前提,产量敏捷性越大、供应商的大数据越充足,该效应越显著。
大数据的上述两种效应对产量敏捷性的影响均取决于两方面:一方面是对需求ε的预测,E[ε|X m]比E[E[ε|X m]|X s]更准确,因而能更好捕捉需求的变化;另一方面是对产量的影响系数,比较E[ε|X m]和E[E[ε|Xm]|Xs]的影响系数,可知前者的正影响是两倍于后者的负影响。由此可见,预测效应不仅能更准确地捕捉需求变化,还能对产量有更大影响。因此,预测效应对产量敏捷性的正影响总是比策略效应的负影响更加显著。
供应链的双向透明通过调节预测效应和策略效应而作用于产量敏捷性。一方面,正向透明能同时调节这两种效应。如前所述,本文中批发价格是存在双重边际效应的充要条件,也是存在策略效应的必要条件,为揭示正向透明对两种效应的不同调节作用,可基于批发价格进行剥离分析。先假定w=0(即不存在双重边际效应),则仅存在预测效应。此时,依据(10)式,正向透明能通过增强预测效应而提高产量敏捷性,特别地,当λs=1时,产量敏捷性可达最优。再还原为w>0的情形(即存在双重边际效应),则同时还存在策略效应。此时,正向透明不仅会增强预测效应,也会因提高产量敏捷性而加剧策略效应,因而在λs=1时并不能使产量敏捷性达到最优,然而,由于前者更显著,正向透明对产量敏捷性仍有显著的正影响。另一方面,逆向透明只会影响策略效应,但可能在供应商的大数据不足时为其补充大数据而加剧策略效应,也可能在供应商的大数据充足时限制其对自身大数据的使用而抑制策略效应。例如,若λm=1,则E[E[ε|Xm]|Xs]=E[ε|X m],即策略效应只取决于制造商的大数据,表明逆向透明可能帮助供应商获得制造商的大数据优势,但也可能限制其利用自身的大数据优势。因此,在双向透明的交互作用下,可能因显著加剧策略效应而降低产量敏捷性,也可能因显著加强预测效应而提高产量敏捷性。
3.2 敏捷性绩效分析
大数据的应用价值体现在其为各参与者创造的敏捷性绩效。为进行量化分析,依据定理1,并由(3)-(6)式求解出各参与者的先验利润。设L=16(tm+λst s+1)2(ts+λmt m+1),可得供应商的先验利润为:
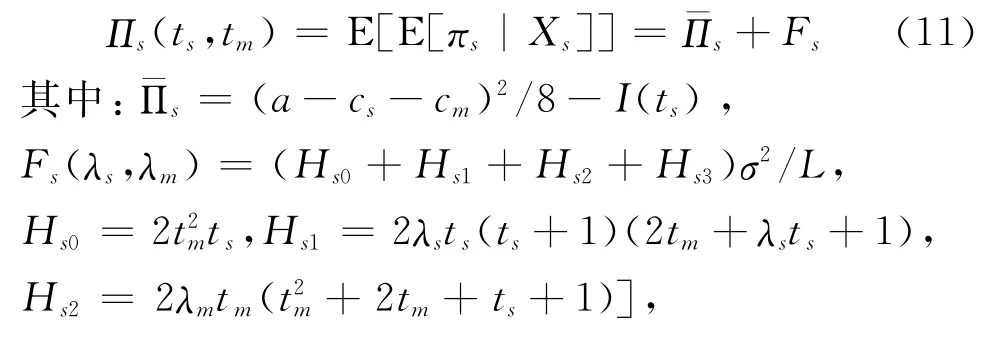

制造商的先验利润为:
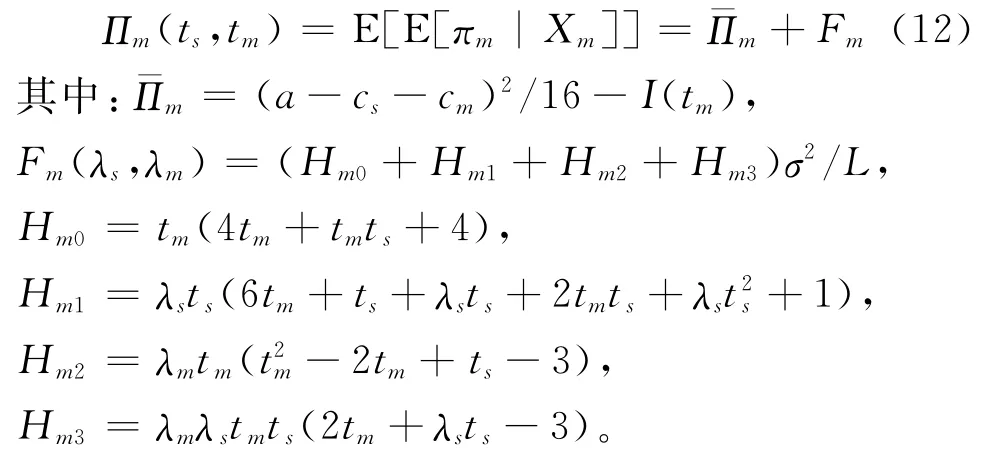
在(11)和(12)式中,和F i分别表示参与者i的确定性和敏捷性绩效。可以验证,Fi>0且与σ2成正比,表明大数据投资总能为各参与者创造敏捷性绩效,且敏捷性绩效随需求波动增大而提高。此外,当tm=λs=0时,Fs=F m=0,可得:
命题1tm+λs≠0,即制造商拥有需求大数据,是供应链获取敏捷性绩效的必要条件。
命题1表明,当tm=λs=0,即制造商不能获取任何大数据时,各参与者的决策均不受大数据影响,从而失去敏捷性。换句话说,下游企业拥有大数据并预测需求,能同时提升自身和整个供应链的敏捷性,因此,自下而上的大数据能力开发对于实现供应链敏捷性具有重要意义。
各参与者的敏捷性绩效不仅取决于需求波动和大数据投资水平,还会受到双向透明的影响。用Fi0=Fi(0,0)表示参与者i在完全不透明时的敏捷性绩效,并用Fi1=Fi(λs,0)-Fi0,Fi2=F i(0,λm)-Fi0和Fi3=Fi(λs,λm)-Fi0-Fi1-Fi2分别表示正向透明、逆向透明和双向同时透明而新增的敏捷性绩效。因此,可用Fi0刻画大数据投资产生的基本收益,Fi1和Fi2刻画正向和逆向透明的独立增值能力,而Fi3则刻画正向和逆向透明的协同增值能力。接下来,分析存在双向部分透明、即λmt mλst s>0时,双向透明对敏捷性绩效的作用路径,从而揭示双向透明对大数据投资决策激励的影响。
命题2双向透明对Fs的影响:
(a)∂Fs1/∂λs>0,∂Fs3/∂λs<0,∂Fs/∂λs>0;
(b)∂Fs2/∂λm>0,∂Fs3/∂λm<0,∂Fs/∂λm>0。
证明求导并由符号分析易得,略。
双向透明能够通过增大产量和批发价格敏捷性而提升供应商的敏捷性绩效。命题2表明,当不存在逆向透明时,正向透明通过增强预测效应和加剧策略效应能同时提高产量和批发价格敏捷性,因而能提高供应商的敏捷性绩效;当不存在正向透明时,逆向透明可能通过抑制策略效应显著提高产量敏捷性,也可能通过加剧策略效应而显著提高批发价格敏捷性,故也可能提升供应商的敏捷性绩效。此外,双向透明同时存在时,彼此间还存在相互抑制作用,从而产生负向溢出效应,如图2的阴影所示。然而,双向透明的独立影响更为显著,因而总体上均有利于供应商的敏捷性绩效。

图2 双向透明对供应商利润的影响路径(ts =3,tm =1,λm =1)
再分析双向透明对Fm的影响。先定义阈值:
(1)ts1=(2tm-1)(tm+1)/(3tm+1),ts2=2tm-1,ts3=4tm-1,ts4=tm+1,ts5=2tm+2,ts6=3tm+3。
(2)λs1= (3tm+1)(ts1-ts)/[ts(ts-ts3)],λs2=2(tm+1)(ts-ts4)/[ts(ts6-ts)],λs3= (ts-ts4)/(2ts),λs4= (ts-ts6)/(4ts),λs5=tm(2ts-ts6)(λm-λm1)/[ts(5λmt m+ts-ts3)],λm1= (3tm+1)(ts-ts1)/[(2ts-ts6)tm],λm2= (ts2-ts)/(3tm)。
引理1(1)0≤λs1≤1⇔ts1≤ts≤ts2,0≤λs2≤1⇔ts4≤ts≤ts5,0≤λs3<1⇔ts≥ts4,0≤λs4<1⇔ts≥ts6,当且仅当ts≤ts1且λm1≤λm≤λm2,或ts1<ts≤ts2且λm≤λm2时,0≤λs5≤1。(2)ts1≤ts2<ts3<ts6,ts1<ts4<ts5<ts6,ts2<ts5,并且,∂tsk/∂tm>0,k=1,2,…,6。
证明依据阈值定义容易直接证得,略。
依据上述阈值定义和引理1,可得命题3。
命题3双向透明对F m的影响:
(a)当且仅当ts≤ts2且λs≥λs1时,∂Fm1/∂λs≤0;当且仅当ts≥ts4且λs≤λs3时,∂Fm3/∂λs≤0;当且仅当ts≤ts2,λm≤λm2且λs≥λs5时,∂Fm/∂λs≤0。
(b)当且仅当ts≤ts6时,∂Fm2/∂λm≤0;当且仅当ts≤ts5且λs≥λs2时,∂Fm3/∂λm≥0;当且仅当ts>ts6且λs≤λs4时,∂Fm/∂λm≥0。
证明见附录。
双向透明能够通过增大产量敏捷性、减小批发价格敏捷性而对制造商的敏捷性绩效产生有利影响。然而,依据命题3,双向透明对制造商的敏捷性绩效并没有确定的影响,取决于各参者的大数据投资水平差异,且彼此间也会产生溢出效应,如图3的阴影所示。命题3a揭示了正向透明的影响规律。可以看到,当ts>max{ts2,ts4},即当供应商的大数据投资水平足够高时,正向透明在独立作用时对产量敏捷性有显著正影响,因而能提升制造商的敏捷性绩效。虽然逆向透明可能在λs<λs3时对正向透明产生负向溢出效应,但正向透明的独立影响更为显著,因而总体上仍能提高制造商的敏捷性绩效。反之,当ts<min{ts2,ts4}时,正向透明在独立作用时既可能在透明度较低时显著增大产量敏捷性,也可能在透明度较高时显著加剧批发价格敏捷性,因而对制造商敏捷性绩效的独立影响呈单峰变化。同时,逆向透明总会对正向透明产生正向溢出效应。由λm≤λm2可得λs1<λs5,故存在λs∈ (λs1,λs5),使得∂Fm1/∂λs<0且∂Fm/∂λs>0。由此表明,即使正向透明有不利的独立影响,但逆向透明产生的正向溢出效应也可能更为显著,因而正向透明仍可能在总体上提升制造商的敏捷性绩效。此外,如图3所示,当供应商的大数据投资水平和逆向透明度都足够低时,制造商的敏捷性绩效可能随正向透明度的提高呈单峰变化,并在λs=λs5达到峰值。也就是说,存在正向部分透明对制造商最有利的情形。值得注意的是,现有文献大多考察完全透明或不透明两种极端情形,因此未能发现部分透明占优的情形。
命题3b揭示了逆向透明对制造商敏捷性绩效的影响规律。可以看到,当ts>ts6时,由∂Fm2/∂λm>0且∂Fm3/∂λm<0可知,逆向透明在独立作用时能显著抑制批发价格敏捷性,因而对敏捷性绩效产生正影响。然而,正向透明也会对逆向透明产生负向溢出效应。因此,当正向透明度较高时,正向透明的溢出效应更显著,导致逆向透明在总体上会降低制造商的敏捷性绩效,而当正向透明度较低时,则逆向透明的独立影响更显著,因而在总体上能提高制造商的敏捷性绩效。反之,当ts<ts5<ts6时,由∂Fm2/∂λm<0且∂F m/∂λm<0可知,虽然正向透明在透明度较高时能对逆向透明产生正向溢出效应,但逆向透明的单独作用对批发价格敏捷性的加剧作用更显著,因而总体上仍会降低制造商的敏捷性绩效。命题3b还表明,制造商的敏捷性绩效总是随逆向透明度的变化而呈现单调变化,而当供应商的大数据投资水平足够高(ts>ts6>tm)且正向透明度足够低时,逆向完全透明也可能对制造商最有利。值得注意的是,现有文献大多假定ts=0或ts=tm,即研究ts≤tm的情形,因而只能得出传统批发价格契约下逆向不透明对下游企业最有利的结论。
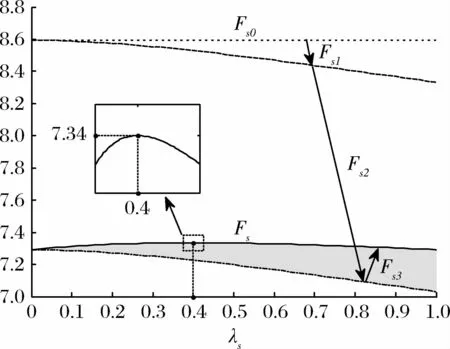
图3 双向透明对制造商利润的影响路径(ts =2,tm =1,λm =0.2)
综上,促进双向透明可能对所有参与者有利。
命题4Fs和F m在λm>λm2或λs<λs5时随λs递增,且在ts>ts6且λs≤λs4时同时随λs和λm递增。
证明由命题2和3可直接得到,略。
命题4表明,当逆向透明度较高或正向透明度较低时,提高正向透明度有利于同时提升各参与者的敏捷性绩效。并且,当供应商的大数据投资水平相对于制造商足够高、且正向透明度足够低时,提高逆向透明度,甚至同时提高双向透明度,均有利于各参与者的敏捷性绩效实现帕累托改进。
4 大数据开发阶段
4.1 大数据投资决策
预期到大数据能产生的应用价值,供应商和制造商同时决策大数据投资水平。依据(11)和(12)式,用V i=Fi-I(ti)表示参与者i的大数据投资利润,则各参与者(i=s,m)的大数据投资均衡 (,)满足:

由∂Πi/∂ti=∂V i/∂ti可知,大数据投资决策取决于其产生的边际利润。显然,只有当大数据投资产生的边际收益大于边际成本时,各参与者才会进行大数据投资。容易验证,故有并 非 总 成 立。 对 于的 情 形,由可知,制造商的最优大数据投资水平总是不会受到成本制约,这显然不符合一般现实,予以排除。因此,仅考虑的情形。该情形下,所有参与者的大数据投资均会受到成本制约,且存在唯一的最优反应函数,因而也能确保(13)式存在纯策略纳什均衡。
定理2设ψ=max{λsσ2/8,(4-3λm)σ2/16},则有ψ∈ [σ2/16,σ2/4]。当I′(0)≥ψ时,各参与者均会放弃大数据投资。并且,当时,存在大数据投资均衡且满足如下条件:

证明见附录。
定理2提供了不同供应链透明度下大数据投资的纳什均衡解算法,并对供应链中的大数据投资可行性进行了判定。由于I′(0)越小、ψ越大,可行性越高,因此,大数据投资可行性取决于三方面因素。首先是大数据技术发展水平,当技术水平较低时,大数据投资的边际成本较高,各参与者的大数据投资收益难以平衡成本投入,因而不会参与大数据投资。其次是需求波动,当需求波动较小时,大数据投资不能获取显著的敏捷性绩效,因而各参与者也会失去投资动机。最后是双向透明度。当正向不够透明时,可能因削弱预测效应而降低供应链的敏捷性绩效;同样,当逆向足够透明时,也可能因加剧策略效应而降低供应链的敏捷性绩效。显然,这两方面都可能因敏捷性绩效不足以弥补成本而阻碍大数据投资。因此,促进正向透明、抑制逆向透明均有利于提高供应链中的大数据投资可行性。
出于对成本函数和供应链透明度的一般性考虑,定理2只限定均衡解的存在条件,而未限定均衡解的唯一性。因此,具体求解中可能出现多重均衡,可从两方面考虑适用性。一方面,直接适用于存在唯一均衡的情形,如满足∂2V i/∂ti∂tj<0,则能够确保均衡解的唯一存在。另一方面,适用于供应链中核心成员可以通过协调机制实现多重均衡精炼的情形。例如,供应商可简单采取“空谈(cheap talk)”等非正式沟通锁定对自己最有利的均衡。特别地,命题5给出了部分适用情形。
命题5(a)当I″(tm)≥σ2/8 时,或当λm≥0.75时,或当λm=0且λs≥0.2时,(b)当λm>2/3且时,∂2V i/∂ti∂tj<0,j≠i,i=s,m。
证明见附录。
命题5表明,当边际成本的增速足够大、逆向透明度足够大、或逆向不透明而正向透明度足够大时,∂2V s/∂t2s<0和∂2V m/∂t2m<0能同时满足,故各参与者的大数据投资存在纯策略纳什均衡。并且,当均衡存在时,双向足够透明有利于确保均衡的唯一性。特别地,当逆向完全透明时,各参与者的大数据投资决策存在唯一的纯策略纳什均衡。
由σ2/16≤ψ≤σ2/4可知,对于任意透明度,供应链在I′(0)≥σ2/4 时不存在大数据投资,而在I′(0)<σ2/16时存在大数据投资。接下来结合特例考察供应链透明度对大数据投资行为的影响。
引理2当I′(0)<ψ时,对于两参与者i和j,j≠i,i=s,m,若∂Fi/∂ti>∂Fj/∂tj,则
证明见附录。
引理2表明,各参与者的大数据投资水平差异取决于其能产生的边际收益。
命题6各参与者的大数据投资决策比较:
当 (λs,λm)= (0,0)时,
当 (λs,λm)= (1,0)时,ψ=σ2/4,且 仅 当
当 (λs,λm)=(0,1)时,
当 (λs,λm)= (1,1)时,
证明见附录。
命题6针对现有研究中较为常见的四种透明度情形,揭示了双向透明对供应链中大数据投资的影响。一方面,当正向不透明(λs=0)时,制造商的大数据投资水平高于供应商,并且,若存在逆向完全透明(λm=1),则ψ值由σ2/4减小为σ2/16,表明逆向透明可能降低投资可行性。另一方面,当正向完全透明(λs=1)时,只有逆向不透明且边际成本足够大时,制造商的大数据投资水平才可能高于供应商,并且,逆向完全透明使ψ值由σ2/4 减小为σ2/8,同样表明逆向透明可能降低投资可行性。此外,当λm=0时,正向是否透明不会改变投资可行性,而当λm=1时,正向透明能提高投资可行性。
命题7双向透明对各参与者投资的影响:当供应商投资大数据时,总有和当制造商投资大数据时,若λm≥2/3,则,若λs≥1/4,则
证明见附录。
命题7表明,供应商通过大数据投资所得边际利润会因正向透明而增加,也会因逆向透明而减少,因此,正向透明或逆向不透明能增大其大数据投资。然而,双向透明对制造商的大数据投资边际利润有着不确定的交互影响。例如,逆向足够透明时,正向透明可能减少制造商的边际利润,因而减少其大数据投资;正向足够透明时,逆向透明也会减少制造商的边际利润,因而减少其大数据投资。因此,针对命题6的四种情形,供应商的投资水平分别在(λs,λm)=(1,0)和 (λs,λm)= (0,1)时达到最高和最低,而制造商的投资水平在 (λs,λm)= (1,1)时达到最低。上述也表明,当正向透明度足够高时,逆向透明可能降低所有参与者的大数据投资水平。
4.2 基于投资补偿契约的大数据开发合作
供应链中各参与者对大数据的分散投资可能会忽视彼此产生的外部性,从而导致决策激励失调。为此,用Fsc=Fs+Fm表示应用大数据实现的系统价值,并用V sc=V s+V m=Fsc-I(ts)-I(tm)表示大数据投资的系统利润。为揭示激励问题,先考察大数据投资可集中决策的基准情形。该情形下,最优大数据投资()可由Kuhn-Tucker条件得到:

比较(15)与(14)式易知,分散与集中决策的本质区别在于各参与者在分散决策时不会考虑其大数据投资对其它参与者可能产生的外部性,即∂F j/∂ti。当∂F j/∂ti>0时,参与者i的大数据投资会对参与者j产生正向外部性,而当∂F j/∂ti<0时,则会产生负向外部性。这种外部性会受到供应链透明度的影响。
命题8当tmt s≠0时,总有∂Fs/∂tm≥0,且仅当 (λs,λm)= (1,0)时取等号。并且,当 (λs,λm)=(0,0)时,∂Fm/∂ts<0;当 (λs,λm)= (1,0)时,当且仅当时,∂Fm/∂ts<0;当 (λs,λm)=(0,1)时,∂Fm/∂ts=0;当 (λs,λm)=(1,1)时,∂F m/∂ts>0。
证明见附录。
命题8表明,大数据投资产生的外部性会受到供应链透明度的影响。可以看到,制造商的大数据投资只会在正向完全透明而逆向完全不透明时不产生外部性,而在其它情形下总是会产生正向外部性。供应商的大数据投资产生的外部性则不确定,可能在双向完全不透明时产生负向外部性,也可能在双向完全透明时产生正向外部性,而在仅有逆向透明时,则不会产生外部性。并且,这种外部性还受到大数据投资水平的影响,例如,当仅存在正向透明时,供应商的大数据投资会在制造商的大数据投资水平足够高时产生负向外部性,也可能在制造商的大数据投资水平较低时产生正向外部性。
供应链中各参与者在大数据投资决策时不能内化潜在的外部性,是导致大数据投资激励失调的根本原因。依据命题8,制造商不会因忽视外部性而导致大数据投资激励过度,而供应商忽视外部性则既可能在双向完全透明时导致大数据投资激励不足,也可能在双向完全不透明时导致大数据投资激励过度。并且,各参与者的大数据投资还存在相互影响,容易看到,在满足∂2V i/∂ti∂tj<0,即彼此存在相互抑制作用时,即使制造商的大数据投资不存在外部性,但供应商的大数据投资却可能因忽视潜在的负向外部性而存在投资激励过度,因而也可能降低制造商的投资边际利润,导致制造商的投资水平低于集中决策时的最优水平。由此可见,只有当所有参与者的大数据投资都不存在外部性时,供应链中才不会出现大数据投资激励失调。然而,只有(λs,λm)=(1,0)且满足时(取决于成本函数,且可验证,线性成本函数不能满足),∂Fs/∂tm和∂Fm/∂ts才可能同时为零,否则,供应链中大数据的分散投资,总会存在激励失调问题。为解决该问题,考虑各参与者基于大数据投资补偿契约进行合作。该契约下,制造商和供应商的目标支付由投资利润和转移支付组成,设T(ts,tm)为转移支付,则分别为V m+T和V s-T。具体契约设计通过求解如下优化问题完成:
上式中,参与约束条件(IR)确保各参与者通过大数据合作均能实现帕累托改善,激励相容条件(IC)实现各参与者按系统最优目标(OBJ)进行决策,即内化大数据投资产生的外部性。
命题9设即采用线性投资补偿契约时,
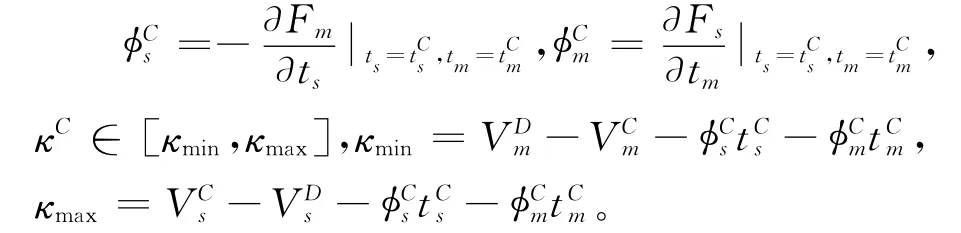
证明见附录。
命题9 给出了大数据投资补偿契约的设计方案,该契约能够协调各参与者的大数据投资激励,也就是说,不仅能使大数据投资达到集中决策时的最优水平,还能实现各参与者在大数据投资利润上的帕累托改善。主要通过两方面实现:一方面,和为大数据投资补偿系数,用以调节各参与者的投资激励,即内化大数据投资的外部性。例如,当∂Fs/∂tm>0时,制造商因忽视正向外部性而存在大数据投资激励不足,因而需要通过设置增加其预期利润,使其有足够的投资激励。由于∂Fs/∂tm≥0,故总有当∂Fm/∂ts<0时,供应商因忽视负向外部性而存在大数据投资激励过度,因而需要设置以降低其投资激励。另一方面,κC为固定转移支付,用以实现系统剩余利润在供应商和制造商之间任意分配,并确保二者均不会因合作而遭受损失,如图4所示。当κC=κmin时,可表示制造商在合作中足够强势,因而能获得全部因合作增加的系统利润,而供应商也不会因合作而遭受损失;反之,当κC=κmax时,同样可表示供应商足够强势,因而能获得全部由合作产生的系统剩余。现实中,两种极端之间的分配情形更为常见,一般基于合作双方的谈判能力而最终确定。
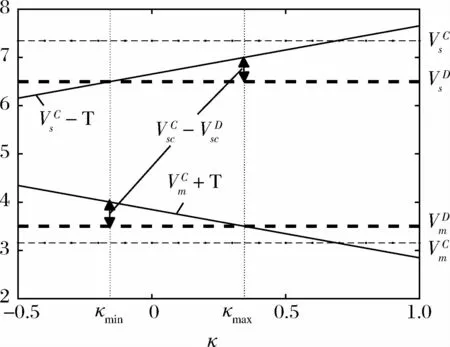
图4 契约合作下各参与者对系统剩余的分配(λs =1,λm =1)
面向共同的产品市场和大数据服务产业,供应链中的上下游企业对大数据的应用价值和成本结构容易形成共识,即存在一致的先验信息,如通过长期的业务合作与技术交流、依据相同的调查报告、采用第三方评估机构等。并且,契约中转移支付函数的三部分设置也有现实可操作性,例如,可表示供应商向制造商直接提供的技术支持与帮助,其中:可表示供应商向制造商分享的大数据能力,而κC则可表示制造商为获得供应商的支持和分享而付出的合作启动费或服务采购费。因此,该契约具有可实施性。另一方面,大数据预测不仅能提高产量敏捷性,还可能在更多方面创造敏捷性绩效,如产品创新、减少供需不匹配等,并且,采用其它预测方法预期到的敏捷性绩效也可能存在差异。为此,命题9提供的契约框架并不受敏捷性绩效和成本结构具体形式的影响,实际上,仅取决于大数据投资产生的边际价值。因此,该契约框架还具有较好的普适性。下节将用数值方法展示双向透明度的全面影响,以强化和扩展管理学启示。
5 数值分析
上文理论结论不受大数据投资成本结构的影响,为构建算例,不妨将投资成本函数设为非线性形式,即I(t)=t2,并且,由于大数据投资利润与确定性需求(a)无关,故对需求波动(σ)的大小设置不会影响算例结果的适用性,不妨设σ2=100。由(14)和(15)式给定优化算法,运用MATLAB 软件编程求解,并依据命题9计算契约参数。为更好趋近理论结果,选取较小的0.01作为双向透明度的步距,共产生10201组算例结果,均存在唯一均衡解。由此绘制图5-7,可直观考察双向透明对于大数据投资决策与利润、以及合作契约设计的影响规律。
图5为双向透明对合作前后大数据投资决策的影响趋势图,观察发现:
1)对于无合作情形,依据图5a-c,提高逆向透明度会同时降低各参与者的大数据投资水平;而提高正向透明度虽有利于提升供应商的大数据投资水平,但却会降低制造商的大数据投资水平。并且,供应商的大数据投资水平仅在正向与逆向透明度足够高时高于制造商,表明促进双向透明能使供应商产生比制造商更强的大数据投资激励。
2)对于有合作情形,依据图5d-f,当双向透明度较低时,供应商退出大数据投资对系统更有利,此时制造商的大数据投资水平主要受到逆向透明度的负影响;而当双向透明度较高时,双向透明仍然有利于供应商提高大数据投资水平,但却会降低制造商的大数据投资水平。并且,由于制造商参与大数据投资总是对系统更加有利,因而在合作情形下制造商的大数据投资水平高于供应商。

图5 双向透明对大数据投资水平的影响

图6 双向透明对大数据投资利润的影响
3)对比两种情形,由图5g-i可见,不合作时,制造商总存在大数据投资不足,而供应商仅在双向透明度足够高时出现大数据投资不足,而更多情形下会出现大数据投资过度。因此,当双向透明度足够高时,二者均可能存在大数据投资不足。并且,整个供应链中的大数据投资会在逆向透明较高时出现不足,而在逆向透明度较低时出现过度。
图6为双向透明对合作前后大数据投资利润的影响趋势图,观察发现:
1)对于无合作情形,依据图6a-c,加强双向透明均有利于提升供应商的投资利润。然而,制造商的投资利润会受逆向透明度的负影响,并且可能在逆向透明度较高时受到正向透明度的正影响,也可能在逆向透明度较低时受到正向透明度的负影响。此外,供应商的投资利润在逆向透明度或双向透明度足够高时大于制造商,而在双向透明度较低时小于制造商。数值结果表明,供应商的 投 资 利 润 占 比,,分 别 在 (λs,λm)=(0,1)和 (λs,λm)= (0,0)时达到最高值73.14%和最低值15.21%。
2)对于有合作情形,依据图6d-f,逆向透明度增加会提高供应商的投资利润,但却会降低制造商的投资利润。正向透明在逆向透明度较小时不会影响各参与者的投资利润,而在逆向透明度较高时能提高制造商的投资利润。供应商的投资利润在 (λs,λm)= (0,1)时达最高。并且,类似不合作情形,供应商的投资利润在逆向或双向透明度足够高时也能大于制造商。数值结果还表明,供应商的投资利润占比能在 (λs,λm)=(0,1)时最高达83.33%,但制造商却能在λm=0时获得全部系统投资利润。
3)对比两种情形,由图6g-i可见,合作在逆向透明度较低时会降低供应商投资利润而提高制造商投资利润,但在逆向透明度较高时则有相反影响。然而,合作总能提升系统投资利润,且在双向透明度较低时,新增系统利润会更加显著。数值结果还表明,系统投资利润改进率,最低在(λs,λm)=(1,1)时达5.01%,而最高可在 (λs,λm)=(0.09,0)时达49.31%。由此可见,双向透明度越低,促进大数据开发合作的效果越显著。
图7为双向透明对合作契约设计参数的影响趋势图,观察发现:
1)依据图7a,总是受逆向透明度的负影响,且在逆向透明度较低时,会受正向透明度的正影响,而反之则会受正向透明度的负影响,因此在(λs,λm)=(1,1)时最小且为负值,而在 (λs,λm)= (1,0)时取最大值。结合图5g可知,当双向透明度足够高时,供应商的大数据投资存在不足,应设<0以增大其投资激励,而在其它更多情形,则应设>0以削减其过度的投资激励。
2)依据图7b,在逆向不透明时,总有=0。虽然图5h表明制造商存在大数据投资不足,但供应商在此时退出后不会拥有任何大数据,使得制造商的大数据投资不会产生外部性,因而不存在投资不足,不需要进行补偿激励。当逆向存在透明时,由于供应商退出大数据投资也会因逆向透明而拥有大数据,使得制造商的大数据投资仍存在正向外部性,因此,需要设计>0以弥补制造商的大数据投资激励不足。此外,(λs,λm)=(0,1)时制造商的投资不足最显著,故设为最大值。
3)依据图7c-d,当双向透明度或逆向透明度足够高时,总有T>0。结合图6g-h可知,此时合作会减少制造商的投资利润而增加供应商的投资利润,因而需要供应商用转移支付弥补制造商的损失。反之,则需要制造商弥补供应商的损失。此外,当κ增大时,T>0的范围缩小,表明供应商的谈判力增强会减小其向制造商提供补偿的可能性,或增大其向制造商索取补偿的可能性,但这并不影响对大数据投资的协调。数值结果表明,κmax-κmin的值随逆向透明而递减,且在双向透明度低时达到最大值,表明逆向不透明或双向不透明有利于增大利润分配空间,从而使契约合作更容易实施。

图7 双向透明对大数据投资激励与合作的影响
6 结语
如何实现供应链中大数据的可持续开发和应用,是有待研究和解决的重要难题。为此,从双向部分透明的供应链视角,构建大数据开发与应用的两阶段决策模型,揭示双向透明对于大数据应用价值与投资激励的影响,并基于契约设计解决大数据投资的激励失调问题。主要结果表明:
1)双向透明对敏捷性绩效的影响。各参与者均能通过大数据投资获得敏捷性绩效,双向透明总是有利于提升供应商的敏捷性绩效,但对制造商敏捷性绩效的影响并不确定。特别地,当供应商的大数据投资水平和逆向透明度均足够低时,制造商的敏捷性绩效可能随正向透明度呈单峰变化。并且,当供应商的大数据投资水平足够高且正向透明度足够低时,逆向透明能提升制造商的敏捷性绩效。此外,若供应商的大数据投资水平足够高且正向透明度足够低,促进双向透明对所有参与者均有利。
2)双向透明对大数据投资决策的影响。大数据技术水平降低、需求波动减小、逆向透明度提高或正向透明度降低均会降低供应链中大数据投资的可行性。并且,供应商的大数据投资会受到正向透明度的正影响,但会受到逆向透明度的负影响,而制造商的大数据投资则可能同时受到双向透明度的负影响。因此,供应商的大数据投资水平能在正向透明度较高时高于制造商,而在正向透明度较低时低于制造商。
3)双向透明对大数据投资激励的影响。制造商的大数据投资不存在负向外部性,因而只会因忽视正向外部性而存在激励不足,而供应商的大数据投资会在双向完全不透明(完全透明)时加剧(减小)制造商的投资激励不足。供应商的大数据投资可能在双向透明度足够高时因忽视正向外部性而存在激励不足,也可能在双向透明度较低时因忽视负向外部性而存在激励过度,并且,制造商的大数据投资会削弱其正向外部性或增强其负向外部性,因而总是会减小(加剧)供应商的大数据投资激励不足(过度)。进一步地,提出的基于大数据投资补偿的契约合作方案,不仅能使大数据投资达到集中决策时的最优水平,还能实现各参与者的帕累托改进。数值分析表明,供应链的大数据投资利润可在该契约合作方案下提升5.01-49.31%。
附录:
(1)命题3的证明:(a)设z0=ts+3tmt s-tm-2t2m+1,z1=ts-4tm+1,则z0≥0⇔ts≥ts1,z1≥0⇔ts≥ts3.
求解∂Fm1/∂λs得sign(∂Fm1/∂λs)=sign(z0+z1λst s),其中,z0=ts+3tmt s-tm-2t2m+1≥0⇔ts≥ts1,z1=ts-4tm+1≥0⇔ts≥ts3.分析可得:当ts≥ts3>ts1时,由z0>0和z1≥0,可得z0+z1λst s>0;当ts<ts3时,z1<0,则z0+z1λst s≥0⇔λst s≤-z0/z1=λs1ts,且当ts2<ts<ts3时,总有z0+z1λst s≥z0+z1ts>0.因此,当且仅当ts≤ts2且λs≥λs1时,z0+z1λsts≤0.
求解∂Fm3/∂λs得sign(∂Fm3/∂λs)=sign(λs-λs3),故有∂Fm3/∂λs≤0⇔λs≤λs3,且当ts<ts4时,λs3<0,故总有∂Fm3/∂λs>0.
求解∂Fm/∂λs得sign(∂Fm/∂λs)=sign(B0+B1λst s),其中,B0=(3tm+3-2ts)λmt m+z0,B1=z1+5λmt m≥0⇔λmt m≥-z1/5.分析可得:当λmt m>-z1/5时,由B1≥0和B0>0可得B0+B1λst s>0;当λmt m≤-z1/5时,B1<0,B0+B1λst s≤0⇔λst s≥-B0/B1=λs5ts.并且,有λs5<1⇔λm≤λm2,而仅当ts≤ts2时,存在λm2≥0.因此,当且仅当ts≤ts2时,存在λm≤λm2且λs≥λs5,使得B0+B1λst s≤0.
(b)求解∂Fm2/∂λm得sign(∂Fm2/∂λm)=sign(ts-ts6),故∂Fm2/∂λm≤0⇔ts≤ts6.
求解∂Fm3/∂λm得sign(∂Fm3/∂λm)=sign(z0+z1λst s),其中,z0= (2tm+2)(tm-ts+1)≥0⇔ts≤ts4,z1=3tmts+3≥0⇔ts≤ts6.分析可得:当ts≥ts6时,由z0<0和z1≤0,可得z0+z1λst s<0;当ts<ts6时,z1>0,则z0+z1λst s≥0⇔λst s≥-z0/z1=λs2ts,且当ts5<ts<ts6时,总有z0+z1λst s≤z0+z1ts<0.因此,当且仅当ts≤ts5且λs≥λs2时,z0+z1λst s≥0.
求解∂Fm/∂λm得sign(∂Fm/∂λm)=sign(λs4-λs),且仅当ts>ts6时,存在λs4>0,使得∂Fm/∂λm≥0⇔λs≤λs4.
(2)定理2的证明:由Kuhn-Tucker条件可得(14)式.由于大数据投资的边际价值递减,若初始投资不能产生正的边际价值,则各参与者不存在进行大数据投资的动机.由和可 得,当I′(0)≥ψ时,均不会大于零.反之,当I′(0)<ψ时,则总存在i=s,m,满足使得∂V i/∂ti=0存在唯一正实数解.
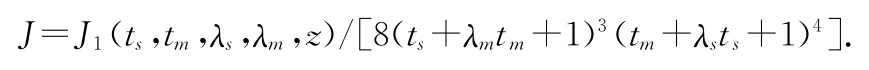
将J1关于ts和t m进行多项式展开,即J1=逐项分析可得仅存在三项可能大于零的系数,即C3,0,C4,0和C0,4.由于C3,0≤0⇒z≥z1,C4,0≤0⇒z≥z2且C0,4≤0⇒z≥z3,故当z≥max{z1,z2,z3}=1/8时,总有J1<0.此外,当λm=0且λs≥0.2时,或当λm≥0.75 时,总 有即
(b) 求 得 ∂2V m/∂tm∂ts= ∂2Fm/∂tm∂ts且sign(∂2Fm/∂tm∂ts) = sign(Jm), 其 中,Jm=,逐项分析Ai,j可知仅有A0,2,A0,3,A0,4,A1,2,A1,3和A2,2等6项可能大于零,且在A0,4=时,均非正.求解A0,4≤0可得,λm=0,或λm>2/3且
类 似 地,易 知 ∂2V s/∂tm∂ts= ∂2Fs/∂tm∂ts, 求 解∂2Fs/∂tm∂ts得sign(∂2Fs/∂tm∂ts)=sign(Js),其 中,Js=逐 项 分 析Bi,j可 知 仅 有B0,1,B0,2,B1,1和B1,2等4项可能大于零,且在B0,1=(λm-1)2-时,均不会大于零.求解B0,1≤0可得,综上,由于λ′s>λ″,故当λm>2/3且λs≥λ′s时,A0,4≤0和B0,1≤0均能满足,因此,总有∂2Fm/∂tm∂ts<0和∂2Fs/∂tm∂ts<0.
(4)引理2的证明:参与者i进行大数据投资时,t Di须满足一阶条件,即依据假定I″(t)≥0,可分两种情形.当I″(t)=0、即为线性成本时,则由I′(t Di)=I′(t Dj) 且 ∂Fi/∂ti> ∂Fj/∂tj可 得,Mi=Mj,因此,仅存在Mi=0>M j的均衡状态,故;当I″(t)>0、即为非线性成本时,由.
(5)命题6的证明:依据定理2直接可得ψ值.再依据引理2,比较∂Fs/∂ts和∂Fm/∂tm的可得的关系.只证明(λs,λm)= (1,0)的情形.比较得∂Fs/∂ts≤∂Fm/∂tm⇔tm≤又 依 据 引 理2,∂Fs/∂ts≤因此,当且仅当满足时,存在
(6)命题7的证明:当参与者i的大数据投资在均衡时必然满足∂V i/∂ti=0,由于,故参与者在不同透明度下的∂V i/∂ti越大,则也越大.并且,同参与者在不同透明度下的成本函数相同,因而,∂Fi/∂ti越大,也越大.因此,只需比较∂Fi/∂ti在不同透明度下的大小即可证得.
(7)命题8的证明:求解∂Fs/∂tm可得,sign(∂Fs/∂tm)=sign(J2),其中逐 项 分析可知所有Ci,j非负,且仅在 (λs,λm)= (1,0)时同时为零,当tmts≠0且 (λs,λm)≠ (1,0)时,总有∂Fs/∂tm>0.求解∂Fm/∂ts,当 (λs,λm)= (1,0)时,可 得sign(∂Fm/∂ts)=sign(z),其中,且仅当tm.其余情形易判断,略.
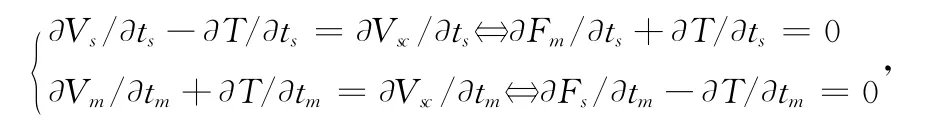
设T=φsts+φmt m-κ,并将其代入上述微分方程组并联立求解,可得和.同时,再代入不等式方程组-T≥和+T≥,联立求解可得κmin≤κ≤κmax,且κmax-κmin=-≥0.
