面向突发事件的应急指挥控制敏捷性度量及仿真*
2016-05-04陶九阳刘方鑫
康 凯,陶九阳,2,刘方鑫
(1.解放军理工大学,江苏南京 210007;2.国防大学,北京 100091)
面向突发事件的应急指挥控制敏捷性度量及仿真*
康凯1,陶九阳1,2,刘方鑫1
(1.解放军理工大学,江苏南京210007;2.国防大学,北京100091)
摘要:现阶段,国内外应急事件时有发生,如何快速有效地实施应急指挥控制是处置社会公共安全突发事件的核心要求之一。因此,以OODA模型为基础提出了一种基于敏捷性指标的应急指挥控制过程模型和一种基于Lotka-Volterra模型的度量指挥控制敏捷性的数学计算方法,并以地铁突发爆炸事故为背景,对应急指挥控制的敏捷性与指挥控制效果进行了仿真分析和对比。
关键词:指挥控制;敏捷性;应急突发事件
发生在人员密集区域的突发事件具有突然性、动态性,这给突发事件的应急处置带来了巨大挑战。探索和研究突发灾难性事件的处置方法、机制、流程等已经成为研究热点。在应急处置过程中,如何才能实现快速有效地应急指挥直接关系到能否妥善高效地处置应急事件,最终减少事件带来的影响和损失。
指挥是军队指挥员及其指挥机关对所属军事力量实施军事行动的特殊组织领导活动[1]。应急事件指挥,与军队指挥属于高度相似的同一活动。由于指挥和控制在实际实施过程中联系紧密,美军一般将指挥与控制合称为指挥控制(C2,Command and Control)[2]。随着信息化、高精度、高速度的武器装备的大量使用,常规的基于作战计划的指挥控制方式面临严峻的挑战,通俗地说就是“计划赶不上变化”。
2008年起,美军指挥控制前沿理论研究计划CCRP(The Command and Control Research Program)开始研究应对复杂、高度动态变化战场的新型指挥控制理论,并于2010年后提出了指挥控制敏捷性(Agility)的概念[3]。指挥控制敏捷性目前已经成为指挥控制领域的一个研究热点。
社会公共安全领域突发事件应急指挥控制,通常都有时间紧迫、情况复杂、形式多变的决策环境特点,这与现代战场态势复杂多变的环境具有相似性。本文通过借鉴军事领域的指挥控制敏捷性的理论成果,立足于公共安全突发事件的应用背景,研究社会公共安全应对复杂突发事件的指挥控制方法和技术,建立一套面向突发事件的应急指挥控制敏捷性的度量方法。
1应急指挥控制过程模型
指挥控制的目的是为了更好地完成任务和应对危机,高效流畅的指挥控制过程是遂行作战活动的有力保证,是各作战单元有效协同的基础。通常,军队指挥控制的过程可以分为态势感知与情况判断、定下行动决心、计划组织作战、协调控制行动和评估战场态势等几个步骤[1]。
在所有指挥控制过程的概念模型中,OODA(Observe—Orient—Decide—Act:观察-调整判断-决策-行动)模型是使用最为广泛的一个模型[4],如图1所示。1987年John R. Boyd在研究战斗机飞行员决策过程时提出了该模型,随后又有大量的改进版本。
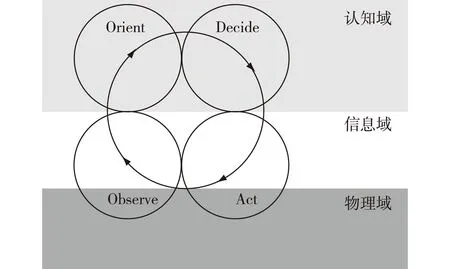
图1 C2过程的OODA环模型
应急指挥控制与普通的军队指挥控制存在着一系列区别,主要表现在:第一,在面临突发事件的应急状态下,时间通常更为紧迫,留给决策者的反应时间更少。反映在OODA模型中,就是指挥控制人员应对OODA环的时间周期更短;第二,在突发情况下,受天气、作业环境等各种自然和社会因素影响,能够用来支撑指挥控制的装备、手段和力量等都可能受到巨大的限制,导致信息的获取、传输、处理受到影响,其直接结果就是决策者会面临更为浓重的“迷雾”,这使得决策者更容易误判形势,制定出不恰当的行动方案,从而造成更大的损失;第三,决策者面临的环境可能高度动态变化,增加其控制局势的难度和复杂度。一方面,突发事件的发生,往往超出决策者的意料,甚至在决策者制定行动方案的过程中,形势又有了新的变化。另一方面,行动的执行者同样面临动态复杂的作业环境,例如火场救火,由于风向经常会突然变化,这可能会导致先前决策者制定的计划瞬间失效。
由此可见,应急指挥控制过程面临时间紧迫、手段受限、环境动态变化等诸多不利因素,如何在有限的时间和资源约束下,使得各项决策的制定科学合理,各项行动的实施及时有效,是有效应对应急突发事件的关键。经过认真分析,我们认为,应急指挥控制模型的建立,应以敏捷性为基本原则,即在有限的时间和资源约束下,制定最为有效的行动方案。这是一个目标优化问题,其关键是设计指标度量体系,建立合适的目标函数,其中,可以根据需要,利用敏捷性作为目标函数或者作为其重要的指标。如何度量应急指挥控制的敏捷性,至关重要。
2应急指挥控制敏捷性度量
当前指挥控制敏捷性的度量普遍采用指标体系法,其主要指标项有响应性、多能性、鲁棒性、创新性、弹性、灵活性、适应性等[5]。这些指标间还会有相互作用,例如实体具备的响应性可以直接对敏捷性的其他指标产生影响。事实上,不同的应用背景和领域,对众多敏捷性指标所造成的影响侧重程度不同,反映在数学上就是指标项的权重不同。在实际应用中,为了简化敏捷性的度量,有时可以只采用几个关键指标进行度量。通过分析可以发现,响应性(responsiveness)和适应性(adaptability)是应急指挥控制敏捷性关注的重点。因为在处理紧急情况时,首先强调的是响应性,即响应时间,在有效的时间内做出恰当的响应是应急指挥控制的核心内容。此外,由于突发事件的复杂性以及态势变化的迅捷性,决定了适应性也是一个重要的考虑方面。在现实中,突发事件的出现,往往不是单一事件的发生,更多地会是一个事件伴随着其他事件的发生而同时或相继发生,例如2015年天津812事件,爆炸引起火灾,消防员进去抢救时,还有爆炸的持续发生,这种突发事件态势发展的高度不确定性要求应急指挥控制需具备较强的适应性。
从宏观来看,应急指挥控制的响应性和适应性具有相关性,并非相互独立。不妨假设,两者在一定程度上存在竞争关系(非严格竞争),其共同消耗有限的资源,这在现实中很常见。例如在应急救援中,投入搜救的人力资源有限,要想增强适应能力,可能需要有冗余的人员待命,遇到再出现其他危机的情况下可以迅速将预备队投入现场;而要想增强响应性,可能需要的搜救人员越多越好,搜救投入人员越多,响应时间越短,于是人员数量对于适应性和响应性就是一种共用的竞争性资源。其他如通信资源、搜救物资、运输资源等都存在这样类似的问题。


(1)
其中δ1表示相对于N2个单位的种群乙,消耗的资源是相对于N1个单位种群甲所消耗资源的δ1倍。
类似地,种群乙的增长方程为
(2)
根据式(1)、(2),可以对响应性和适应性相互竞争的结果进行分析。分析此方程,可以发现它存在平衡点。由此根据Lotka-Volterra模型方法,对式(1)、(2)求导,得到系数矩阵A,根据|A-λE|=0 求解特征方程的根,就可以得到4个平衡点及得到该平衡点的条件,如表1所示。

表1 响应性和适应性均衡解
根据表1可知,其中P1,P2的存在会导致只有一种属性的存在,即要么适应性指标占用全部资源,要么响应性指标占用全部资源,而现实中往往需要综合考虑适应性和响应性,因此P1,P2不符合客观现实,P4相对于实际同样不符合客观现实,只有P3与客观现实相符,可以达到理论上的响应性和适应性均衡。
针对响应性、适应性等影响因素对其进行条件概率的计算,因为面对突发事件的情况下,在满足各属性要求的情况下求得最快事件的概率:
(3)
由于本文是针对响应性和适应性进行分析,其他特性的影响未考虑,所以上述公式可以写为
(4)
基于以上的适应性和响应性指标计算,根据表1的结果,采用加权平均法可以得到应急指挥控制的敏捷性Agl的度量公式:
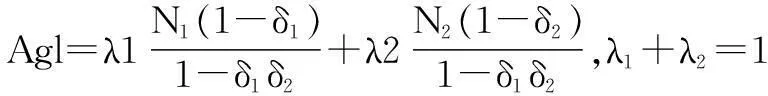
(5)
3案例仿真与分析
为了检验模型与方法的有效性,本文以地铁突发事件的应急指挥控制为例,进行仿真检验计算。
地铁一般都处在半封闭空间里,具有人流基数大、设备密度高的特点,一旦发生突发事件,人员疏散和救援非常困难。
仿真案例想定设定假设地铁发生突发事件(例如:爆炸)需要进行人员疏散。
仿真模型基于Lotka-Volterra模型对敏捷性度量中的适应性和响应性进行仿真实验,采用R语言进行仿真实验和数据可视化展示。
仿真参数和过程设定假设当前地铁内需要疏散的人数为300。设定三种人员疏散策略:1)第一种方案是每个人自由疏散,这里设定每个人朝距离最近的出口处移动;2)第二种方案是在地铁中有人指挥,进行人员疏散,这里主要是指挥人员间的协调配合。例如如果存在一个出口1疏散人流较小,这时指挥人员A给予该区域人员指示“朝出口1进行移动”。同时,如果指挥人员B也发现出口1疏散人流较小,也对B区域人员发送疏散指令“朝出口1移动”,就会由于过度指挥造成出口1人流瞬间增大,出现拥挤甚至可能会引发踩踏问题;3)第三种方案,就是每个人有一台移动终端,发生突发事件后,每个人根据移动终端的提示进行最优路线的撤离。在想定中考虑到爆炸发生后,可能会有爆炸的情况发生。本仿真实验假定最多发生两次爆炸,爆炸位置随机选取。三种移动方案的仿真参数测量中,以在某一时刻人口疏散的数目作为敏捷性指标中响应性的度量;以出现二次事故时,安全区域的人员数目(成功疏散人员数目)作为敏捷性指标中适应性的度量。本文做了两个实验,实验1主要对响应性指标进行了仿真计算度量,其中曲线斜率的变化可以在一定程度上表征适应性。实验2主要针对敏捷性度量指标中的适应性进行了仿真计算检验。仿真参数设定如表2所示。实验结束后,统计人员疏散情况(即人员到达出口位置),全部人员疏散时间,冲突人数及人员密度的实验数据,如图1、2所示。

表2 仿真参数设置
实验1响应性指标仿真分析:疏散人员数目随时间的变化。
如图1所示,横坐标代表仿真时间,纵坐标表示疏散人数。其中绿色曲线代表第一种疏散策略、红色曲线代表第二种疏散策略、蓝色曲线代表第三种疏散策略,对图中曲线进行比较可知,如果每个人都根据手持移动设备的引导进行移动,效果最优,疏散人数最多,在设定的场景下,能够成功疏散的人数约占总人数的87.3%;通过疏散指挥人员进行调度指挥的,疏散人流数目也远优于人群盲目移动的效果,但是在1920s到1950s之间出现单位时间内疏散人流数目下降的情况,分析是由于上面提到的指挥人员的协调不够,出现多处人流引入一个疏散方向导致人流拥挤的现象。
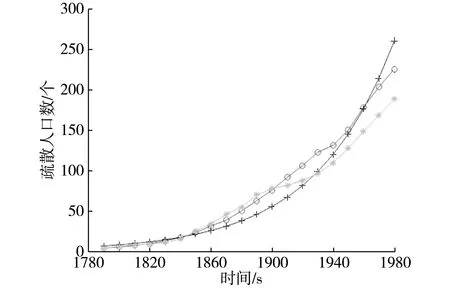
图1 疏散人口时间图
实验2适应性指标仿真分析:二次爆炸时成功疏散的人员密度。
设定二次爆炸的发生,对其中一处出口处的人流百分比进行统计。图2中(a)表示第一种策略、(b)表示第二种策略、(c)表示第三种策略,可以看出相同人员密度范围内越平滑的曲线疏散的效果越好,可知第二种有指挥人员的策略优于自由逃离的情况,第三种根据手持设备的策略不仅平滑变化,并且人口密度概率低,可知这种策略是最理想的情况。

图2 二次爆炸出口处人员密度图
4结束语
本文基于Lotka-Volterra模型分析了敏捷性度量中的两种重要指标响应性和适应性,并分析了二者的均衡情况,最后以地铁爆炸疏散为背景进行了案例分析。本文的研究主要侧重于敏捷性度量指标中的响应性和适应性之间常见的竞争平衡。事实上,敏捷性度量指标还有很多,如鲁棒性、灵活性等,而且各类指标之间也存在多种相互关系,系统的研究各类指标在应急指挥控制敏捷性度量方面的表现形式及计算方法,是需要进一步研究的重点。另外,如何运用敏捷性的度量体系改善指挥控制的敏捷性,也是需要研究的内容。
参考文献:
[1]任海泉. 军队指挥学[M].北京:国防大学出版,2007.
[2]Alexander Kalloniatis, Iain Macleod, Formalization and Agility in Military Headquarters Planning[J]. The International C2 Journal:CCRP, 2010.
[3]Alberts, David S., Agility,Focus and Convergence:Adapting C2 to the 21st Century[J]. TheInternational C2 Journal, 2007.
[4]李敏勇, 张建昌. 新指挥控制原理[J]. 情报指挥控制系统与仿真技术,2004,6(2):10-16.
[5]David S. Alberts.敏捷性优势[M]. 闫红伟,宋荣,译. 北京:兵器工业出版社,2012.
[6]Nikolay A. Kudryashov, Analytical properties and exact solutions of the Lotka-Volterra competition system[J]. Applied Mathematics and Computation Journal,2015.
Command and Control Agility Measurement and Simulation Facing the Sudden Matters Emergency
KANG Kai1, TAO Jiu-yang1,2, LIU Fang-xin1
(1.PLA University of Sci. & Tech., Nanjing 210007;2.National Defense University PLA China, Beijing 100091, China)
Abstract:At this stage, emergency incidents occur in the domestic and international,Effective emergency command and control is the kernel of the disposal of public safety emergencies. Based on the OODA model this paper presents a new model of command and control process face the sudden matters emergency based on the index of agility, establishes a mathematical model based on Lotka-Volterra model, and simulation analysis and comparsion is carried out on the agility of command and control face the emergency and the effect of command and control in the background of the subway explosion accident.
Key words:C2; agility; sudden matters emergency
中图分类号:TP399-CB;E91
文献标志码:A
DOI:10.3969/j.issn.1673-3819.2016.02.005
作者简介:康凯(1986-),男,山东成武人,硕士研究生,研究方向为应急指挥控制。陶九阳(1984-),男,博士研究生,讲师。刘方鑫(1992-),男,硕士研究生。
*基金项目:国家自然科学基金(61174198;U1435218)
收稿日期:2015-12-16
文章编号:1673-3819(2016)02-0020-04
修回日期: 2015-12-22
