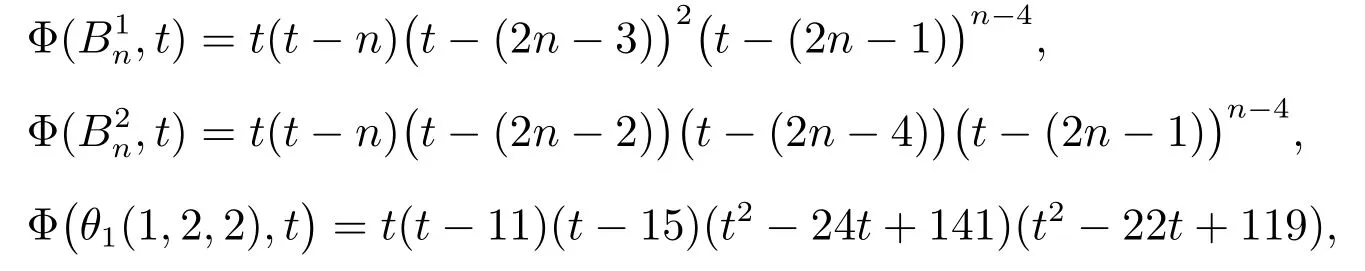The Bicyclic Graph with the Minimum Distance Laplacian Spectral Radius

FAN Dan-dan, NIU Ai-hong, WANG Guo-ping,

(1- College of Mathematical and Physical Sciences, Xinjiang Agricultural University, Urumqi 830052;2- School of Mathematical Sciences, Xinjiang Normal University, Urumqi 830054)

Abstract: The largest eigenvalue of the distance Laplacian matrix of a connected graph G is called the distance Laplacian spectral radius of the graph G.In this paper we obtain a sharp lower bound of distance Laplacian spectral radius,and then using the bound we determine the unique graph which has the minimum distance Laplacian spectral radius among all unicyclic graphs.Finally,by using the bound again as well as the characteristics polynomial of a distance Laplacian matrix, we characterize the unique graph with the minimum distance Laplacian spectral radius among all bicyclic graphs.

Keywords: distance Laplacian spectral radius; unicyclic graph; bicyclic graph

1 Introduction

The distance spectral radius of a connected graph has been studied extensively.Bose et al[1]obtained the graph with the maximum distance spectral radius in the class of graphs without a pendant vertex.Yu et al[2,3]determined the graphs having maximum and minimum distance spectral radius among graphs with a given number of pendant vertices and among unicyclic graphs, respectively.Ili[4]determined the graph with the minimum distance spectral radius among the trees with given matching number.Nath and Paul[5]characterized the graphs with the minimum distance spectral radius among all connected bipartite graphs with a given matching number and a given vertex connectivity, respectively.Stevanoviand Ili[6]determined the graph with the maximum distance spectral radius among the trees with fixed maximum degree.

Aouchiche and Hansen[7]introduced the distance Laplacian and distance signless Laplacian spectral of graphs, respectively.Xing and Zhou[8]gave the graphs with the minimum distance and distance signless Laplacian spectral radius among bicyclic graphs with fixed number of vertices.Xing et al[9]determined the graphs with the minimum distance signless Laplacian spectral radius among the trees,unicyclic graphs,bipartite graphs and the connected graphs with fixed pendant vertices and fixed connectivity, respectively.Aouchiche and Hansen[10]proved that the star Snattains the minimum distance Laplacian spectral radius among all trees of order n.Lin and Zhou[11]determined the graphs with the minimum distance Laplacian spectral radius among the connected graphs with fixed number of pendant vertices and the fixed connectivity, respectively.

In this paper, we determine the graphs with minimum distance Laplacian spectral radius among unicyclic and bicyclic graphs, respectively.

2 Main results

If x = (x1,x2,··· ,xn)Tthen it can be viewed as a function defined on V(G) ={v1,v2,··· ,vn} which maps the vertex vito xi, i.e., x(vi)=xi.Thus we have

which shows that LD(G) is positive semidefinite.

Suppose that x is an eigenvector of LD(G) with respect to the eigenvalue µ.Then

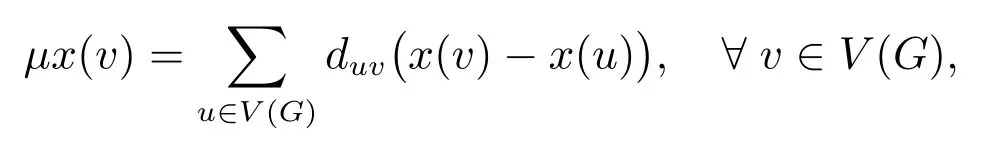
and we call x an eigenvector of G with respect to µ.Throughout the paper, we denote by ∂(G) the distance Laplacian spectral radius of G.

Let tracemax(G) be the maximum transmission of vertices of G.Then we have:

Lemma 1[12]Let G be a connected graph.Then ∂(G)>tracemax(G)+1.

Suppose that G and H are two graphs.Then we write GH if G and H are isomorphic, and GH otherwise.

Let Snbe the star on n vertices, andbe the unicyclic graph on n vertices obtained by joining two pendant vertices in Sn.Aouchiche and Hansen[13]conjectured thatattains the minimum distance Laplacian spectral radius among all unicyclic graphs.This has been verified by Tian et al[14].Here we again verify it by the direct computation which is more simple.

Theorem 1Let G be a connected unicyclic graph on n ≥6 vertices.Then∂(G) ≥=2n − 1 with equality if and only if

ProofBy a simple computation we can obtain=2n − 1.

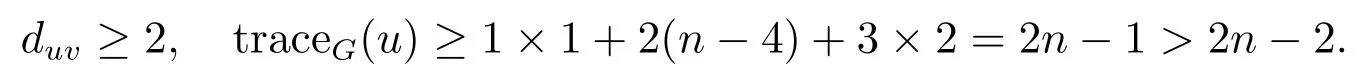
So we next assume that G ∈ Ck,n−k.

Case 1k =3.Suppose that G is isomorphic to the graph H1which is shown in Figure 1,where 1 ≤ n1≤ n2, n3=0 or 1 ≤ n1≤ n2≤ n3.Note that n=n1+n2+n3+3.In this case we can choose a pendant vertex v, and by a simple computation we obtain that traceG(v)=(2n − 2)+(n2+n3− 1) ≥ 2n − 2.

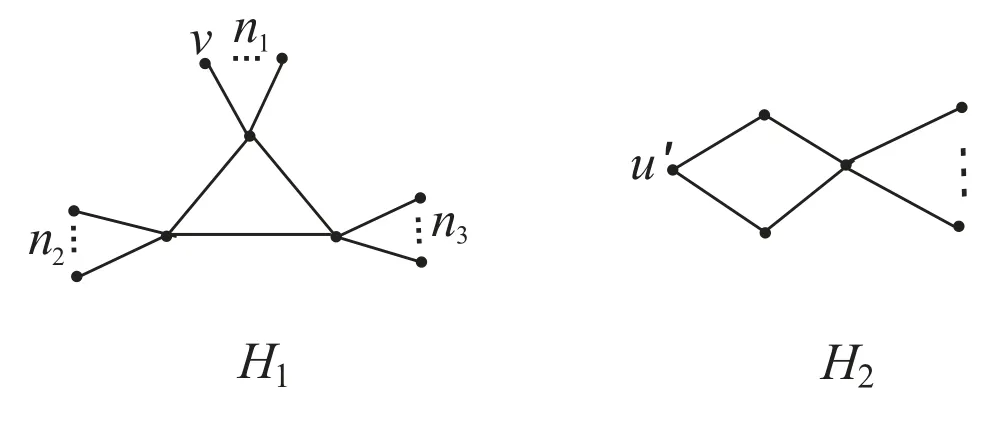
Figure 1: The graphs H1 and H2

Case 2k =4 or 5.Suppose that k =4.If G is isomorphic to the graph H2which is shown in Figure 1,then since n ≥ 6,we easily obtain that traceG(u′)=3n−8 ≥ 2n−2,and otherwise we can choose a pendant vertex v′such that

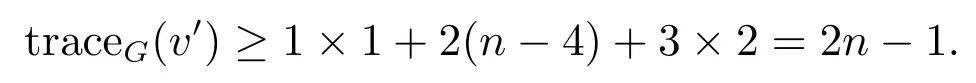
Therefore,tracemax(G)≥ 2n−2.When k =5 we can similarly prove that tracemax(G)≥2n −2.

Case 36 ≤ k ≤ n−1.We denote bythe graph of Ck,n−kwhere Ckcontains only one attached vertex.It is easy to know that if `v and u′′are respectively pendant vertices of G andthenNote that

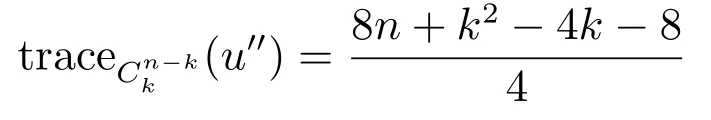
if k is even, and otherwise

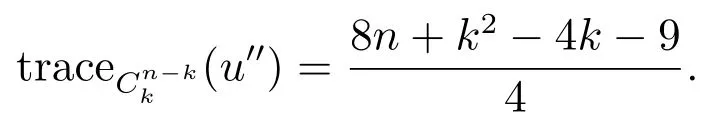
Therefore, tracemax(G)>2n −2.

Case 4GCn.Then tracemax(Cn)=if n is even,and otherwise tracemax(Cn)Thus, tracemax(Cn) ≥ 2n − 2 if n ≥ 7.

By a simple computation we can obtain that ∂(C6) = 13 and so by Lemma 1 we know the result is true.

Connected graphs in which the number of edges equals the number of vertices plus one are called bicyclic graphs.Define a b-graph to be a graph consisting either of two vertex-disjoint cycles C1and C2and a path P joining them having only its end-verticesandin common with the cycles, or two cycles C1and C2with exactly one vertexin common.The former is called b1-graph and the latter b2-graph.Define a θ-graph to be a graph consisting of two given vertices u0and v0joined by three paths P1, P2and P3with any two of these paths having only the given vertices in common.Obviously,a bicyclic graph is a b-graph or a θ-graph with trees attached.

Denote by θ1(n1,n2,n3)the θ-graph where the path Piis of length ni+1(i=1,2,3)and n3≥ n2≥ n1.Φ(G,t) = det(tIn− LD(G)) is called the distance Laplacian characteristic polynomial of graph G.

Lemma 2Let G be a connected bicyclic graph on 6 vertices.Then ∂(G) ≥∂(θ1(1,1,2)) with equality if and only if Gθ1(1,1,2).

ProofAll bicyclic graphs on 6 vertices are shown in Figure 2.By a simple computation we can obtain that traceGi(w)≥ 10,and so by Lemma 1,we know ∂(Gi)>11 for 1 ≤ i ≤ 11.By direct calculation, we have

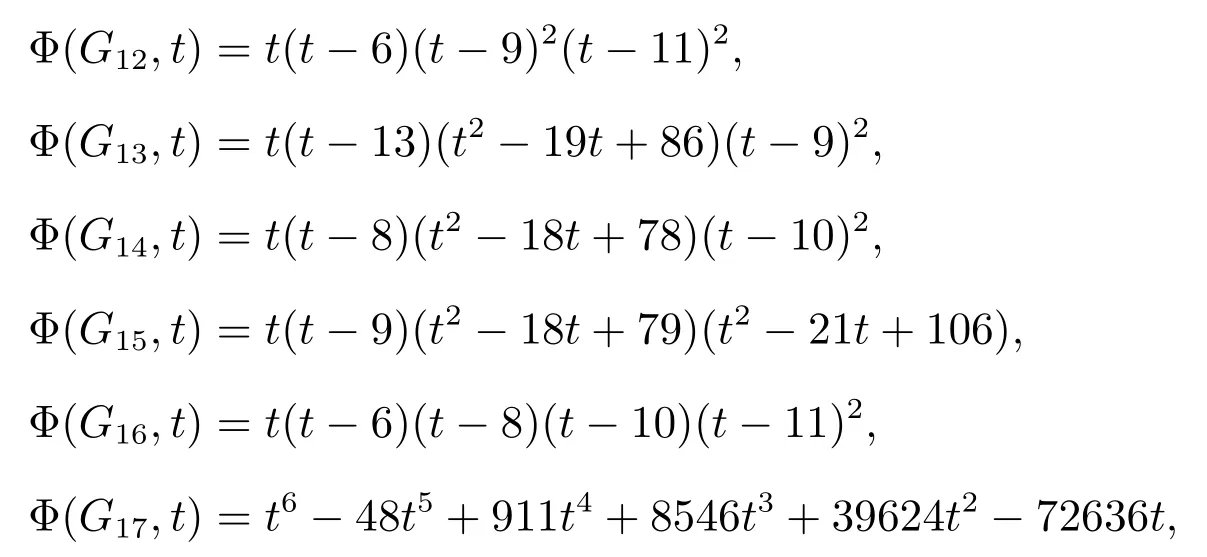
from which we have

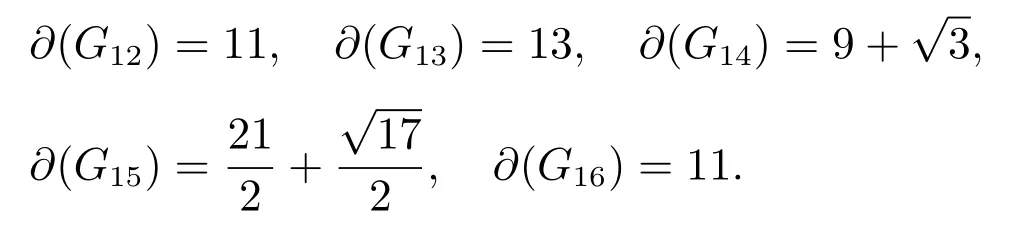
Note that Φ(G17,12) = −720 < 0, and so ∂(G17) > 12.We see G14θ1(1,1,2), and so the result is true.

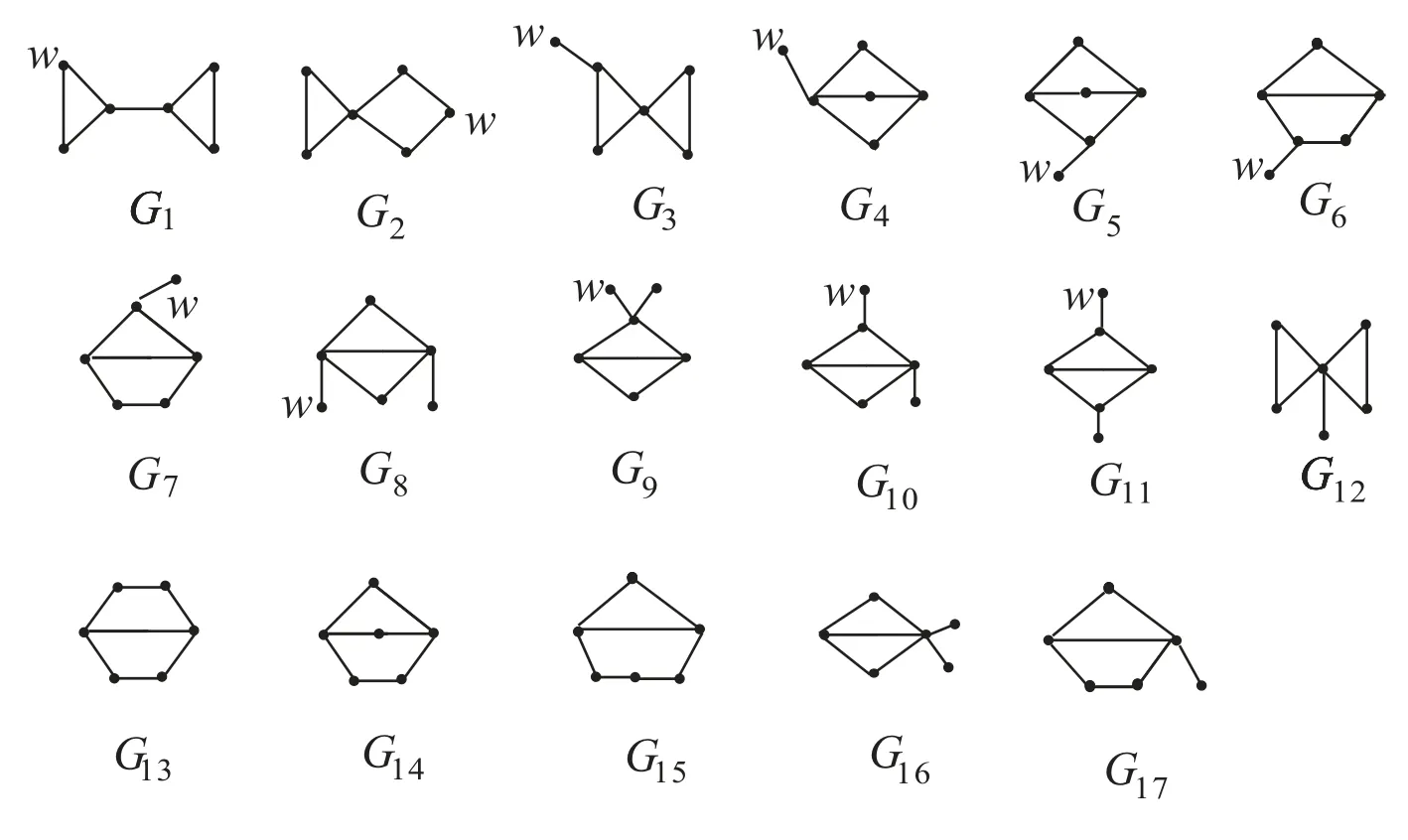
Figure 2: All bicyclic graphs on 6 vertices

Lemma 3Suppose n ≥7.Then we have:

(i) tracemax(G)≥if G is a b-graph on n vertices;

(ii) tracemax(G) ≥ 2n − 2 if G is a θ-graph on n vertices but

(iii) tracemax(G) ≥ 2n − 2 if G is a bicyclic graph with pendant vertices but

Proof(i) Let H3and H4be shown in Figure 3, where w is the vertex which is farthest fromin Ca+1.We easily verify that

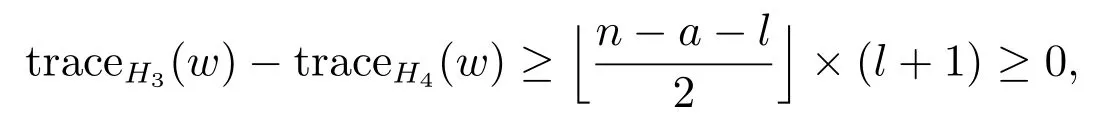
and so traceH3(w)≥traceH4(w).

Figure 3: The graphs H3 and H4

Suppose without loss of generality that a+1 ≤ n − a.Then we haveNow we distinguish two cases to discuss.

Case 1.1If n is odd, thenThus

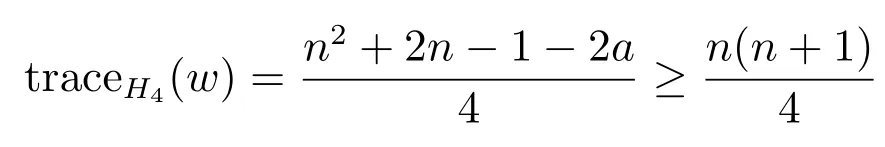
if a is odd, and otherwise traceH4(w)=

Case 1.2If n is even, thenThus

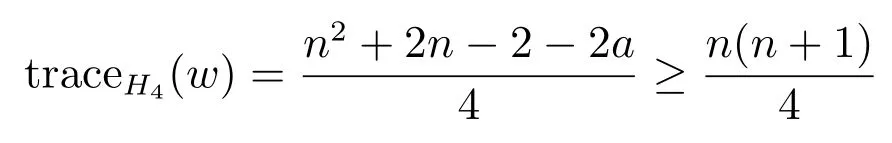
if a is odd, and otherwise traceH4(w)=

These show that (i) is true.

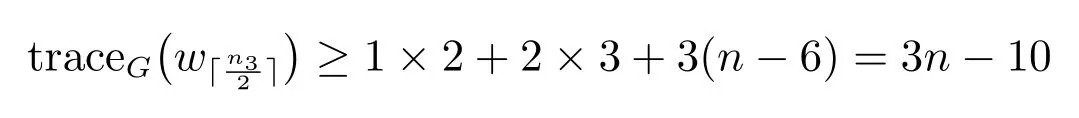
if n ≥8.This shows that (ii) is true.

(iii) Suppose that G is b1-graph with trees attached.If w is a pendant vertex of G, then there must be two vertices u1and u2such that dwu1≥ 3 and dwu2≥ 3, from which we can obtain that

So we assume G is a b2-graph with trees attached.

Denote by Bm1,m2the set of the bicyclic graphs on n vertices which are b2-graphs with trees attached,where Ciis of length mi(i=1,2).Let Cm1,m2consist of the graphs of Bm1,m2which are b2-graphs with edges attached.

Let G ∈ Bm1,m2Cm1,m2.Suppose that Tu∗is a tree attached at u∗∈ Ciand that w∗∈ Tu∗is one of the pendant vertices which is farthest from u∗.Then

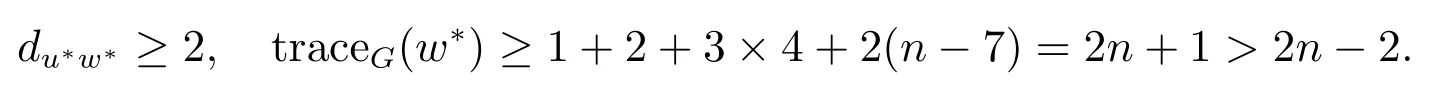
So we next assume that G ∈Cm1,m2.If m1> 3 and m2> 3 then we can choose a pendant vertex w such that

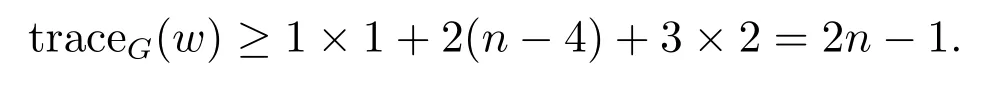
So we can assume without loss of generality that G ∈Cm1,3.Next we distinguish three cases to discuss.

Case 2.1m1=3.Suppose that G is isomorphic to the graph H5which is shown in Figure 4, where n1≥1.

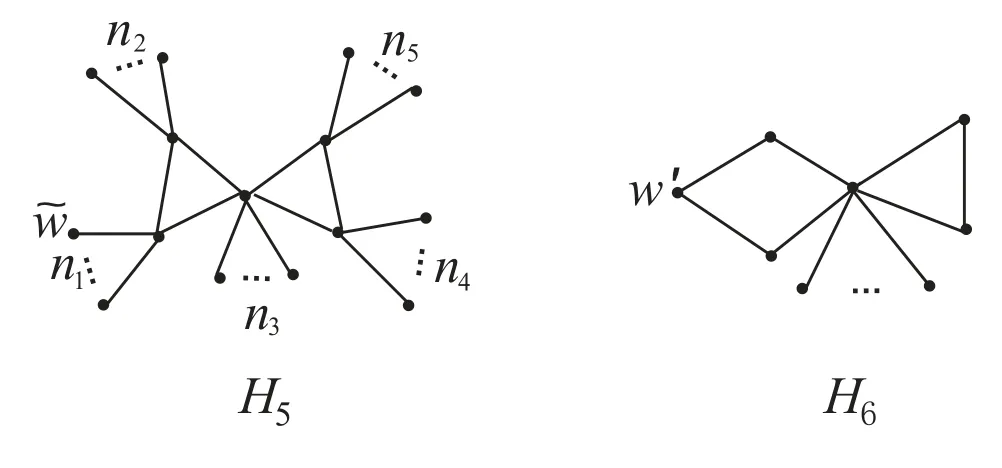
Figure 4: The graphs H5 and H6

Note that n ≥7.Therefore, if nj= 0(j = 2,3,4,5) then we obtain traceG() =2n −1, and otherwise

Case 2.2m1=4 or 5.Suppose that m1=4.If G is isomorphic to the graph H6which is shown in Figure 4 then we easily obtain that traceG(w′) = 3n − 8 > 2n − 2,and otherwise we can choose a pendant vertex w′′such that

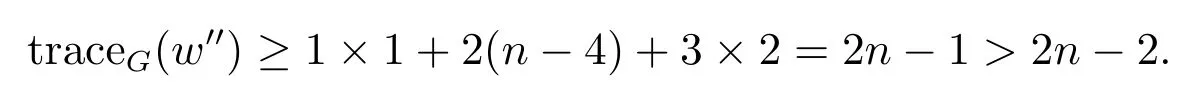
Therefore,tracemax(G)>2n−2.When m1=5,we can similarly prove that tracemax(G)>2n −2.

Case 2.3m1≥ 6.We denote bythe graph of Cm1,3in which only the vertexis attached by edges.It is easy to know that ifand v′′are respectively pendant vertices of G andthenNote that

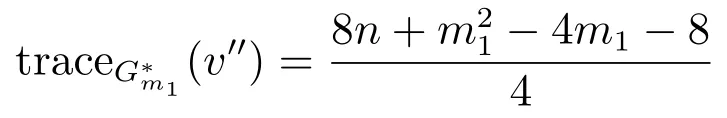
if m1is even, and otherwise

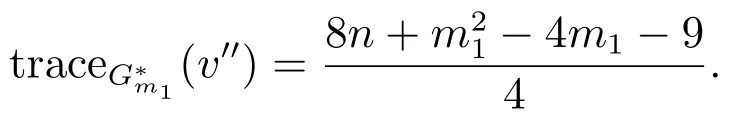
Therefore, tracemax(G)>2n −2.

Denote by P(n1,n2,n3) the set of the bicyclic graphs on n vertices which are θgraphs with trees attached, where Piis of length ni+1(i = 1,2,3).Let(n1,n2,n3)consist of the graphs of P(n1,n2,n3) which are Pni+2with edges attached.

Let G ∈ P(n1,n2,n3)(n1,n2,n3).Suppose that Tv∗is a tree attached at v∗∈Pni+2and that∈Tv∗is one of the pendant vertices which is farthest from v∗.Then dv∗≥2 and so

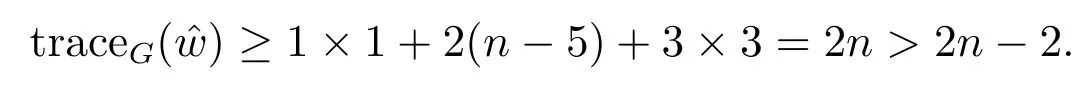
If n3≥n2≥n1≥1 then we can choose a pendant vertexand find another one vertex z such that≥3.Thus

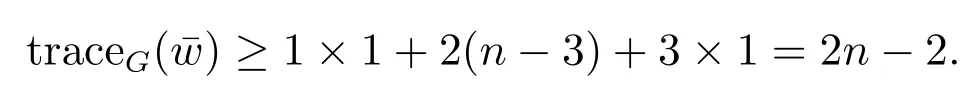
If n3≥n2≥2 and n1= 0, then we can also choose a pendant vertexand find two vertices u1and u2such that≥3(i=1,2).Thus

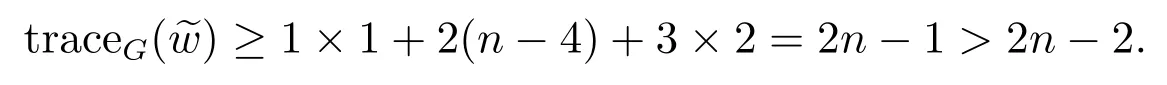
Case 3.1n3= 1.Suppose G is isomorphic to the graph H7which is shown in Figure 5.

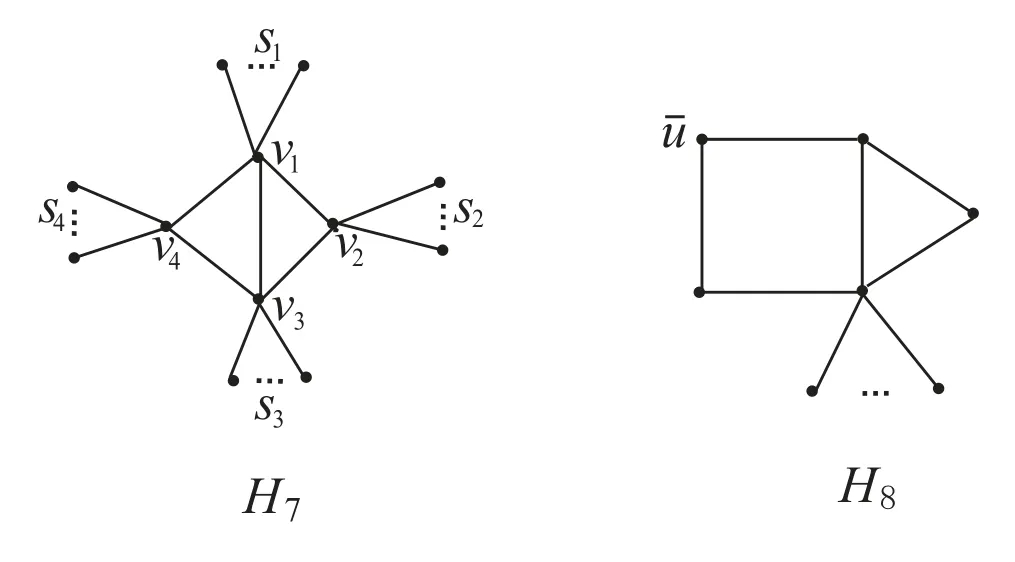
Figure 5: The graphs H7 and H8

If s2= s4= 0, then sincewe have s1≥1 and s3≥1.Suppose thatv1is a pendant edge.Then

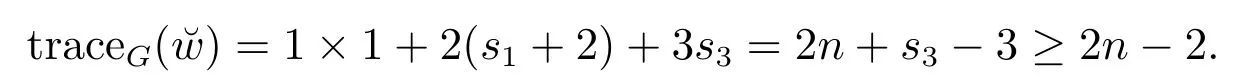
If s20 andis a pendant edge then

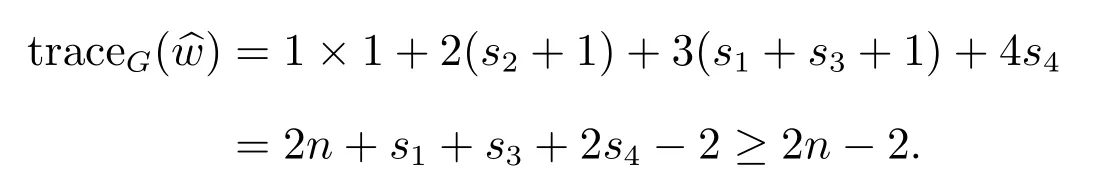
Therefore, tracemax(G) ≥ 2n − 2.If s40, we can similarly prove that tracemax(G) ≥2n −2.

Case 3.2n3=2 or 3.Suppose that n3=2.Note that n ≥7.If G is isomorphic to the graph H8which is shown in Figure 5, then we easily obtain that traceG() =3n−9 ≥2n−2,and otherwise we can choose a pendant vertexsuch that traceG()>2n − 2.Therefore, tracemax(G) ≥ 2n − 2.When n3= 3, we can similarly prove that tracemax(G)>2n −2.

Denote by θ(n1,n2,n3) the graph of(n1,n2,n3) in which only the vertex u0is attached by edges.

Case 3.3n3≥4.It is easy to know that ifandare respectively pendant vertices of G and θ(0,1,n3) then traceG()≥traceθ(0,1,n3)().Note that

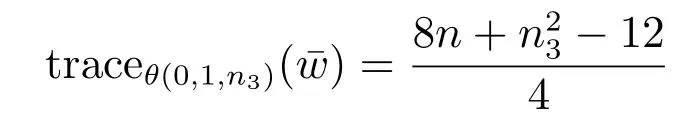
if n3is even, and otherwise

Therefore, tracemax(G)>2n −2.

Theorem 2Suppose that G is a bicyclic graph on n ≥6 vertices.Then we have:

(i) If n=6, then ∂(G) ≥ θ1(1,1,2) with equality if and only if Gθ1(1,1,2);

ProofBy a simple computation we know