方程φe(n) =2tω(n) 的可解性
2020-03-07邓桂林廖群英
邓桂林, 廖群英
(四川师范大学 数学科学学院,四川 成都610066)
1 引言及主要结果
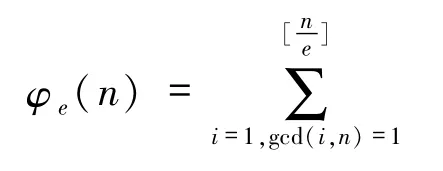
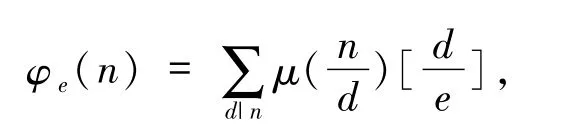
其中,[·]是高斯函数,μ(n)是麦比乌斯函数,即
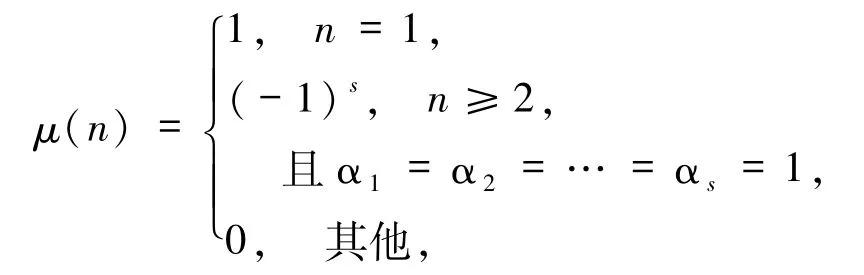
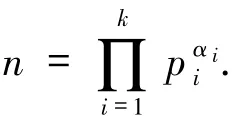
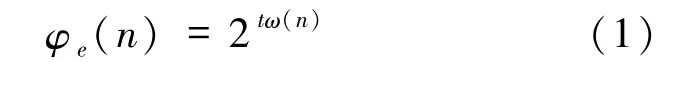
的可解性.
本文给出了e=2 时方程(1)的全部正整数解(即本文定理1.1),以及e=3,4,6 时方程(1)的部分正整数解(本文定理1.2 ~1.4).
定理1.1设t∈Z+,e =2,则方程(1)的全部解为
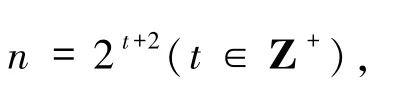
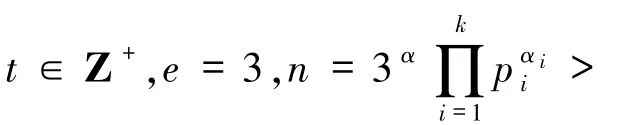
1)若αi=0(1≤i≤k),则方程(1)的解为(n,t)=(9,1).
2)若α∈{0,1}且任意pi≡2(mod 3)(1≤i≤k,mod表示取模),则方程(1)无解.
3)若α=0 且存在pi≡1(mod 3)(1≤i≤k),则方程(1)的解为
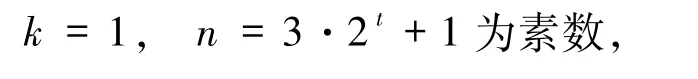
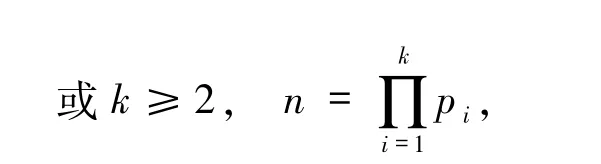
其中,p1=3·2a+1 为素数,pi(2≤i≤k)为费马素数.
4)若α=1 且存在pi≡1(mod 3)(1≤i≤k),则方程(1)的解为
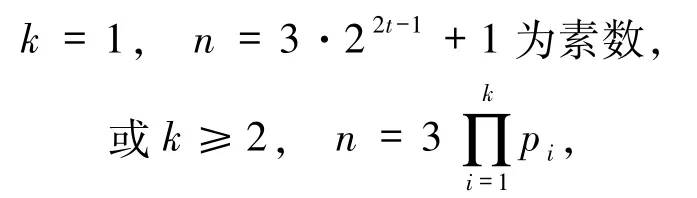
其中,p1=3·2a+1 为素数,pi(2≤i≤k)为费马素数.
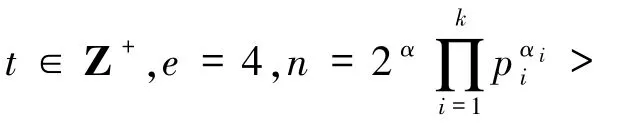
1)若αi=0(1 ≤i≤k),则方程(1)的解为
2)若α=0 且任意pi≡3(mod 4)(1≤i≤k),则方程(1)的解为
(n,t)=(9,1), 或n = 4·2t+3 为素数.
3)若α∈{0,1}且存在pi≡1(mod 4)或α≥2,则方程(1)的解为
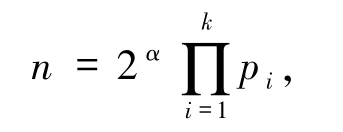
其中pi(1≤i≤k)为费马素数.
定理1.4设t∈Z+,e=6,
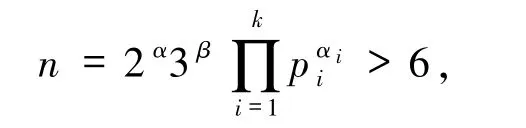
其中,整数α,β,αi≥0,pi为不同的奇素数且gcd(pi,6)=1(1≤i≤k).
1)若αi=0(1≤i≤k),则方程(1)的解为n =9·22t+1.
2)若α=0,β≥2,则方程(1)的解为
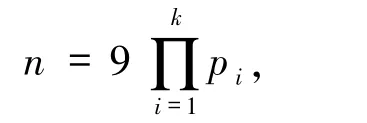
其中pi(1≤i≤k)为费马素数.
3)若α=1,β≥2,则方程(1)的解为
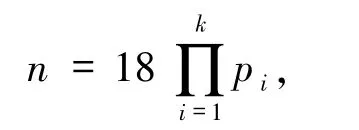
其中pi(1≤i≤k)为费马素数.
4)若α=β=0 且存在pi≡1(mod 6),则方程(1)的解为
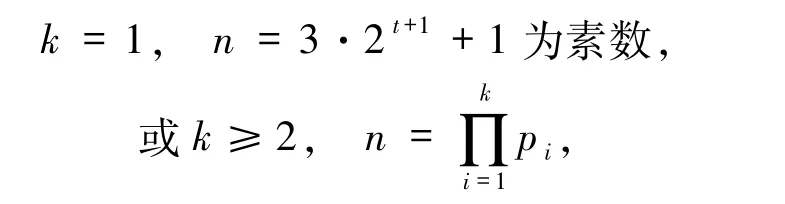
其中,p1=3·2a+1 为素数,pi(2≤i≤k)为费马素数.
5)若α=0,β=1 且存在pi≡1(mod 6),则方程(1)的解为

其中,m =3·22t+1,p1=3·2a+1 均为素数,pi(2≤i≤k)为费马素数.
6)若α=1,β=0 且存在pi≡1(mod 6),则方程(1)的解为
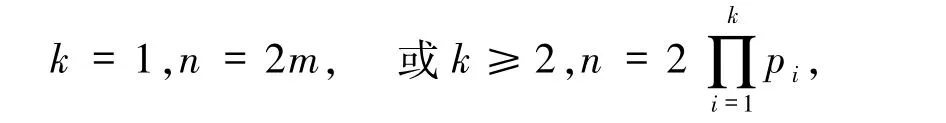
其中,m=3·22t+1+1,p1=3·2a+1 均为素数,pi(2≤i≤k)为费马素数.
7)若α=β=1 且存在pi≡1(mod 6),则方程(1)的解为
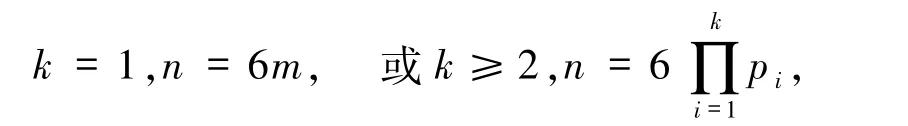
其中,m =3·23t+1,p1=3·2a+1 均为素数,pi(2≤i≤k)为费马素数.
8)若α≥2,β=0 且存在pi≡1(mod 6),则方程(1)的解为
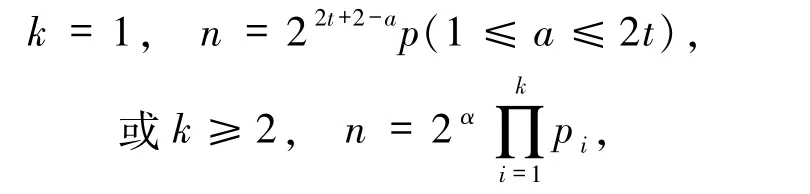
其中,p=p1=3·2a+1 为素数,pi(2≤i≤k)为费马素数.
9)若α≥2,β=1 且存在pi≡1(mod 6),则方程(1)的解为

其中,p=p1=3·2a+1 为素数,pi(2≤i≤k)为费马素数.
定理1.5设t∈Z+,e=6,
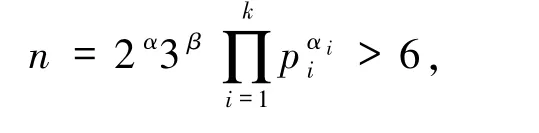
其中,整数k,α,β,αi≥0,pi为不同的奇素数且gcd(pi,6)=1(1≤i≤k),则如下条件之一成立时,方程(1)无解.
1)α=β≥2 且存在pi≡1(mod 6).
2)α=β=1 且任意pi≡5(mod 6)(1≤i≤k)或α≥2 且β=1.
注1.6迄今为止,已知的费马素数只有5个[6]:F0,F1,F2,F3,F4.在1≤k≤5 的情况下,定理1.1 ~1.5 的解见附录.
2 一些引理
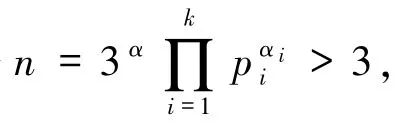

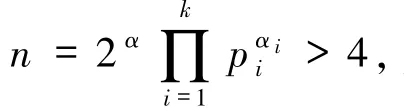

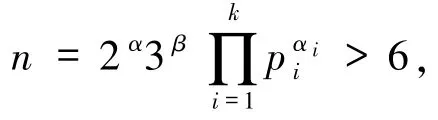
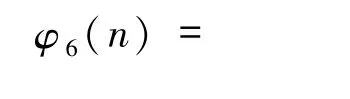
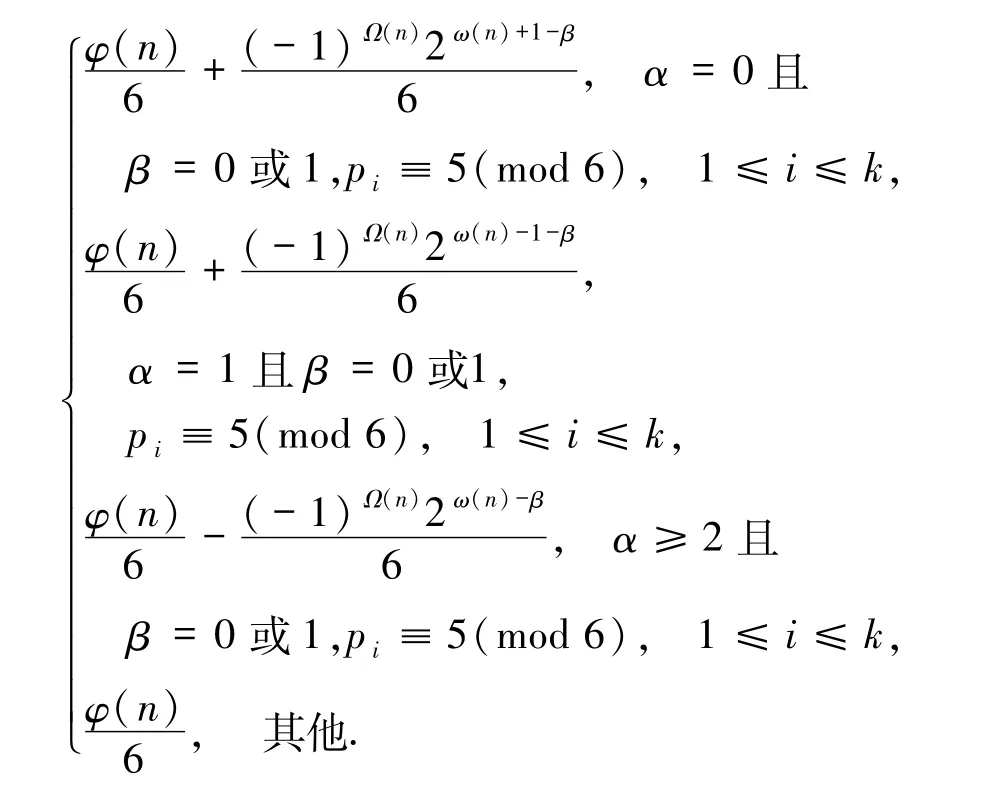
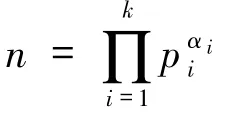
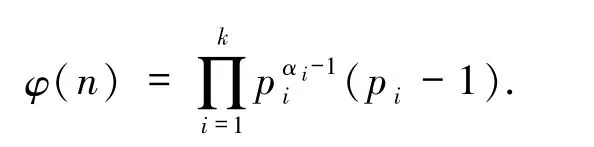
引理2.5[10]丢番图方程x2+7 =2y仅有正整数解
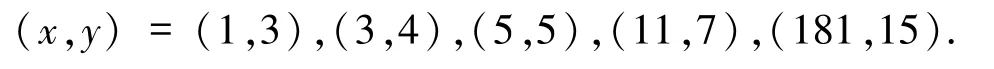
在引理2.1 ~2.3 中要求k≥1.在引理2.1 中,当k = 0 时,即n = 3α>3,根据φ3(n)的定义,φ3(3α)等于序列1,2,…,3α-1中与3 互素的数的个数,故
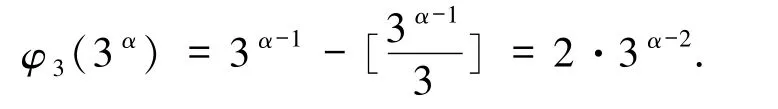
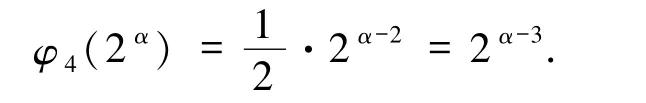

引理2.6若n=2α3β>6,则
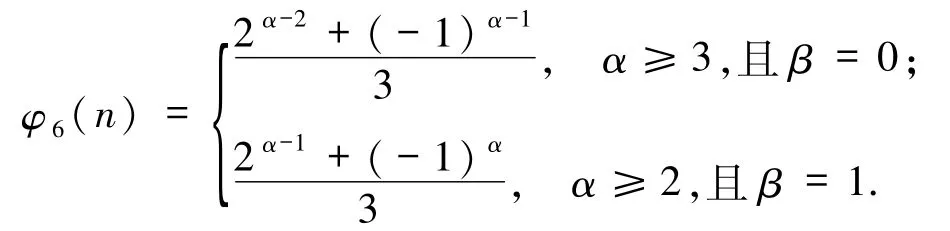
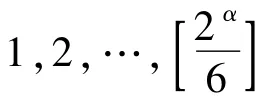
(i)若α -1 为奇数,则2α-1≡2(mod 3),故
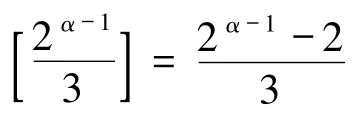
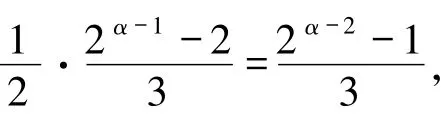
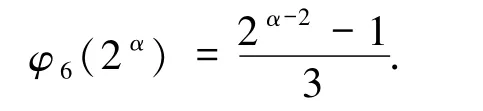
(ii)若α -1 为偶数,则2α-1≡1(mod 3),
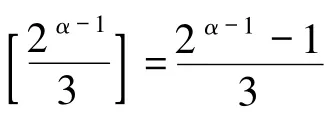
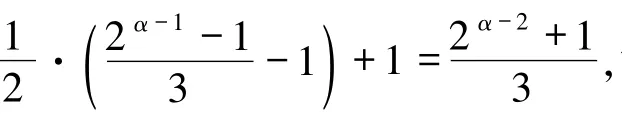
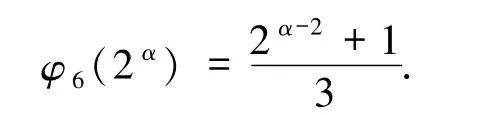
综上,当α≥3 时,
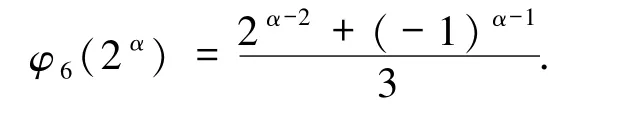
2)若n=3·2α,其中α≥2,根据广义欧拉函数的定义,φ6(3·2α)等于序列中与3·2α互素的数的个数,即序列1,2,…,2α-1中既与2 互素又与3 互素的数的个数.易知序列1,2,…,2α-1中2 的倍数的数的个数为的倍数的数的个数为,因6 的倍数的数的个数为,故由容斥原理得
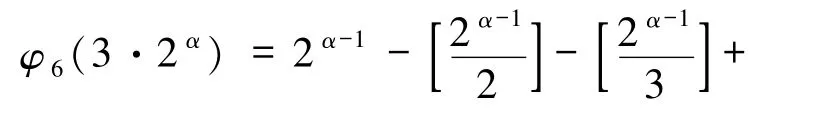
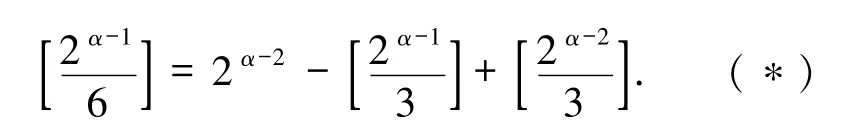
(i)若α -1 为奇数,则2α-1≡2(mod 3),2α-2≡1(mod 3),故
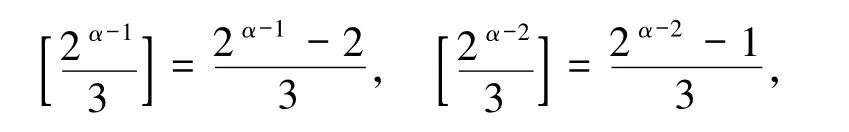
从而由(*)式得
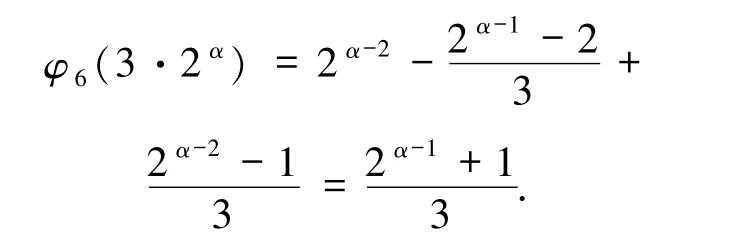
2)若α - 1 为偶数,则2α-1≡1(mod 3),2α-2≡2(mod 3),故
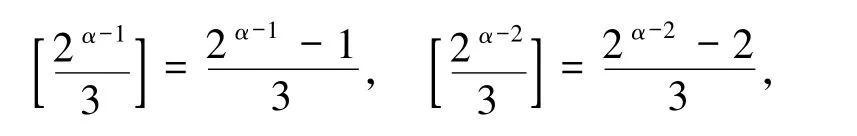
从而由(*)式得
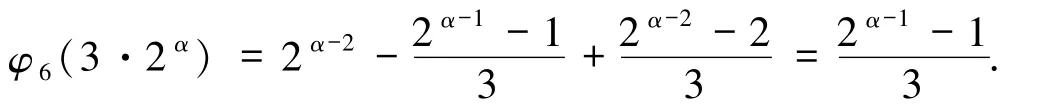
综上,当α≥2 时,
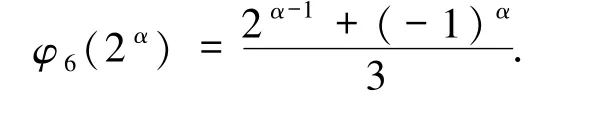
这就完成了引理2.6 的证明.
3 主要结果的证明
定理1.1 的证明e =2 时方程(1)等价于φ(n)=21+tω(n).
当n=1 时,φ(n)= φ(1)=1,但由ω(n)=ω(1)= 0 知21+tω(n)= 21,矛 盾.当n = 2 时,φ(n)=φ(2)=1,但由ω(n)=ω(2)=1 知

综上,完成了定理1.1 的证明.
定理1.2 的证明e=3 时.
2)若任意pi≡2(mod 3).当α =0 时,即n =
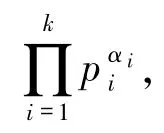
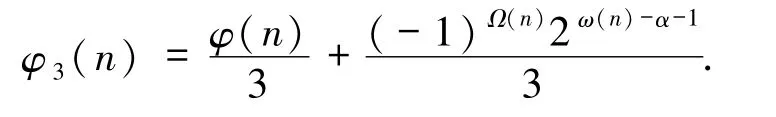
于是由方程(1)得
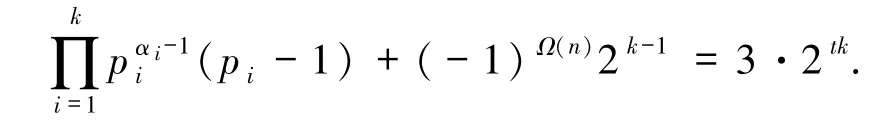
又t∈Z+,故两边同时除以2k-1得
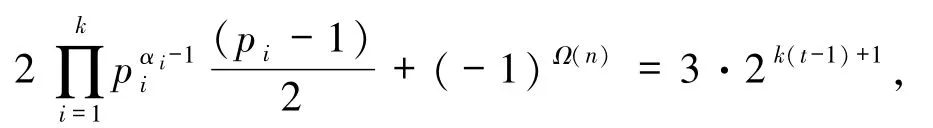
等式两边奇偶性不同,矛盾,故方程(1)无解.又由已知α=0,1 可知必有α=1,即且
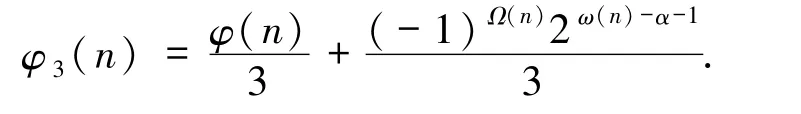
于是由方程(1)得
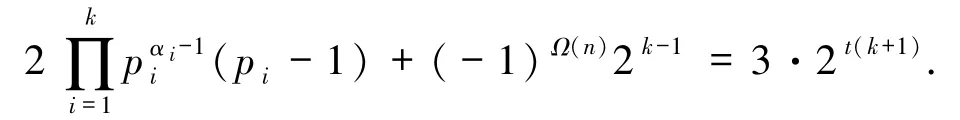
又t∈Z+,故等式两边同时除以2k-1得
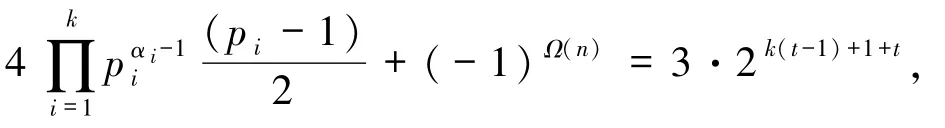
等式两边奇偶性不同,故方程(1)无解.
3)当α=0 且存在pi≡1(mod 3)时,即n =,故ω(n)=k,从而由引理2.1 知φ3(n)=则由方程(1)可得
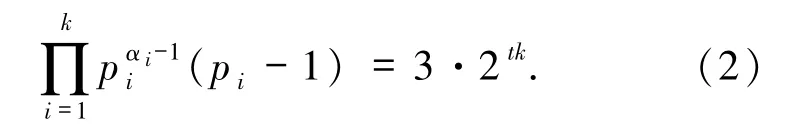
4)证明类似3).
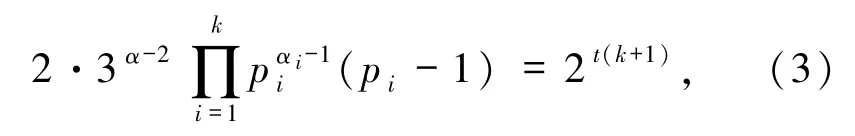
由gcd(pi,3)=1,比较等式两边2 的个数,可得α=且,故其中pi(1≤i≤k)为费马素数.
综上,完成了定理1.2 的证明.
定理1.3 的证明若e=4.
2)当α=0 且任意pi≡3(mod 4)时,即n =,故ω(n)=k,从而由引理2.2 可知
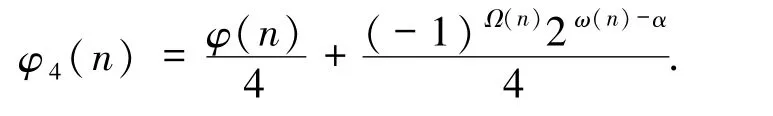
于是由方程(1)可得
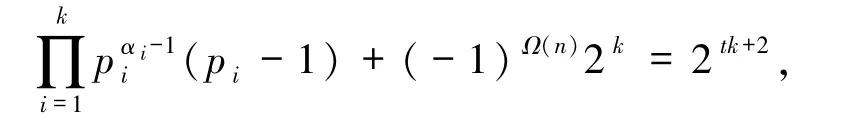
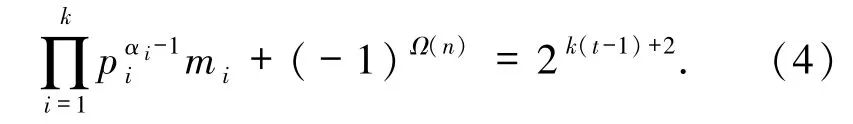
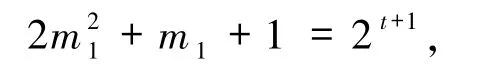
3)设奇数n的标准分解式为
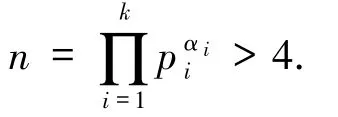
(i)若α =0 且存在pi≡1(mod 4),即n =
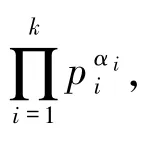
(ii)若α=1 且存在pi≡1(mod 4),证明类似于(i).
(iii)若α≥2,类似定理1.1 中的2).
综上,完成了定理1.3 的证明.
定理1.4 的证明e=6 时.
当α≥3,β =0 时,即n =2α,由引理2.6 可知2α-2+(-1)α-1=3·2t,矛盾,故方程(1)无解.
当α=β=1 时,即n=6,故φ6(n)=122t,此与t∈Z+矛盾.
当α≥2,β=1 时,即n =3·2α,由引理2.6 可知2α-1+(-1)α=3·22t,矛盾,故方程(1)无解.
当α=0 且β≥2 时,即n =3β,由引理2.3 知φ6(n)=3β-2.故由方程(1)得3β-2=2t,即β =2,t=0,与t∈Z+矛盾.
当α=1 且β≥2,即n =2·3β,由引理2.3 知φ6(n)=3β-2.故由方程(1)得3β-2=22t,即β =2,t=0,与t∈Z+矛盾.
当α = β ≥2 时,n = 2α3β,由 引 理2.3 知φ6(n)=2α-13β-2.故由方程(1)得2α-13β-2=22t,即α=2t+1,β=2,从而n=9·22t+1(t∈Z+).
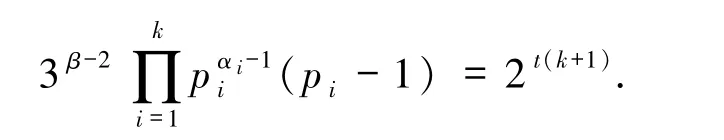
又pi是与6 互素的奇素数,故,β =2,即n =
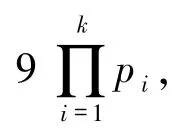
3)证明类似于2).
4)若α=β=0 且存在pi≡1(mod 6),即n =
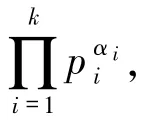
于是由方程(1)知
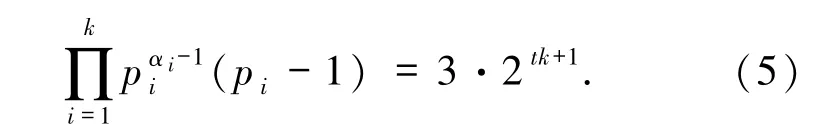
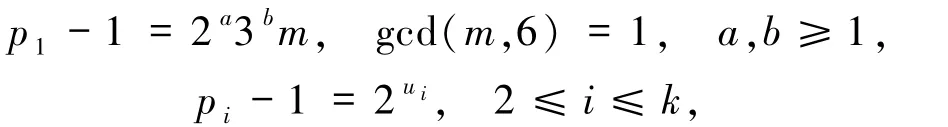
即pi(2≤i≤k)为费马素数.
5)~7)的证明类似于4).
8)若α≥2,β =0 且存在pi≡1(mod 6),即
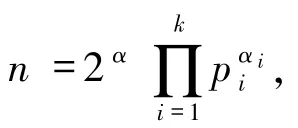
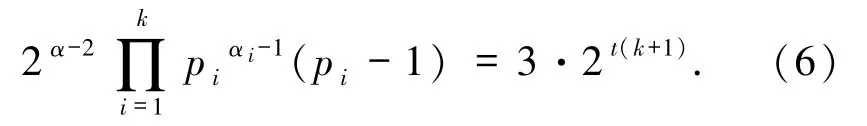
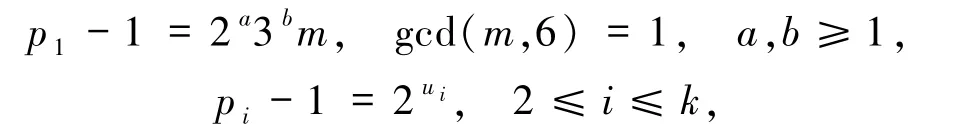
故pi(2≤i≤k)为费马素数.
9)证明类似于8).
综上,完成了定理1.4 的证明.

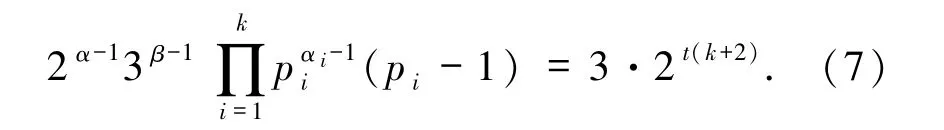
k=1 时,由(7)式可知
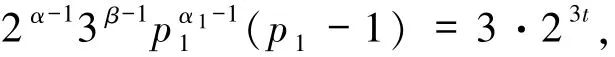
又由p1≡1(mod 6),从而且m(gcd(m,6)=1,a,b≥1),注意到gcd(m,6)=1,故m=1,β+b=2.又β≥2,故b =0,从而p1为费马素数且p1≢1(mod 6),故方程(1)无解.若k≥2,不妨设p1≡1(mod 6),此时由(7)式可知对任意的i=1,2,…,k,均有且
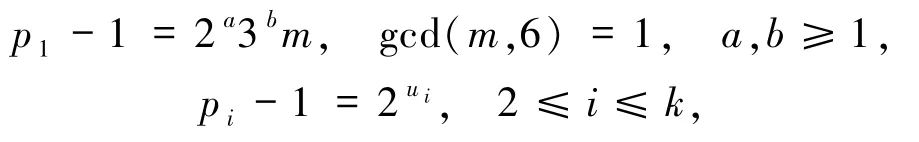
此与存在pi≡1(mod 6)矛盾.
2)若pi≡5(mod 6)且α=β=1,即
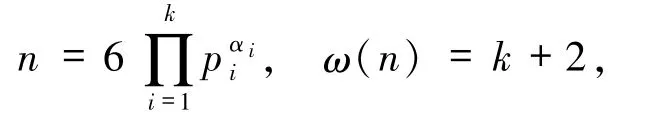
由引理2.3 可得
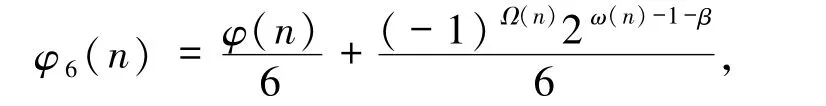
故由方程(1)得
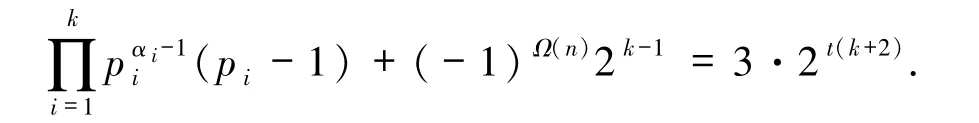
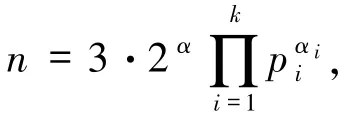
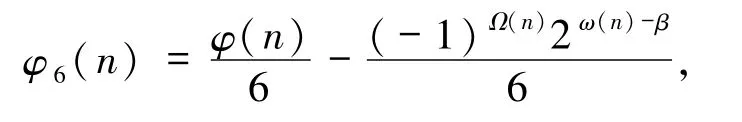
再由方程(1)得
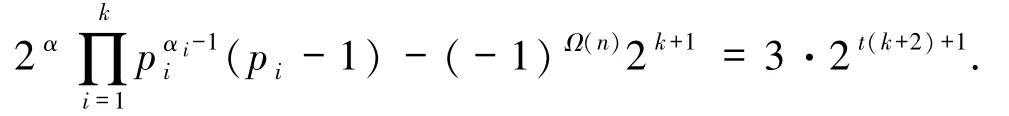
注意到t∈Z+,α≥2,在等式两边同时除以2k+1,比较等式两边因子2 的个数知等式两边奇偶性不同,故方程(1)无解.
综上,完成了定理1.5 的证明.
4 补充说明
若1≤k≤5,利用已知的费马素数,可求出对定理1.1 ~1.4 的具体解.为节约篇幅,此处只给出定理1.1 和定理1.2 的具体求解过程,定理1.3 和定理1.4 的具体求解过程留给有兴趣的读者,对应结果请参见文末的附录.
4.1 定理1.1 证明的1)和2)1)若α =0,则
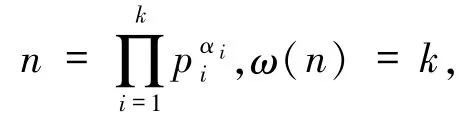
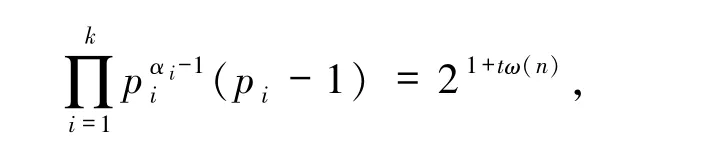
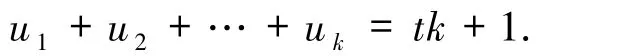
类似可得:
(t,n)=(1,F0F1),(2,F0F2),(4,F0F3),(8,F0F4).
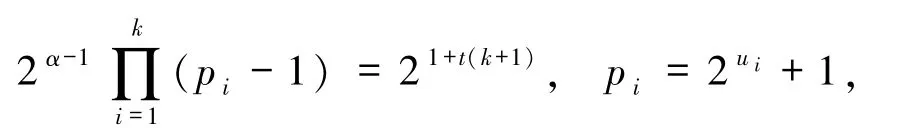
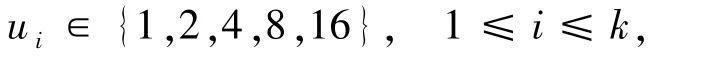
且
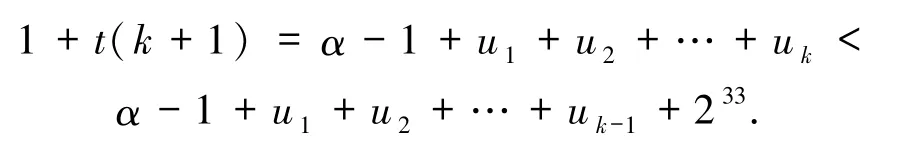
依次取k=1,2,3,4,5 计算,得到t≤230+1.下面在t≤230+1 的假设下讨论方程(1)的可解性及其解.
当k=1 时,1 +2t=α-1 +u1,又由u1∈{1,2,4,8,16}知α∈{2t,2t +1,2t -2,2t -6,2t -14},从而
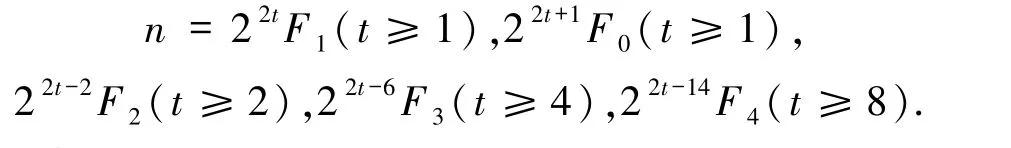
类似可得:
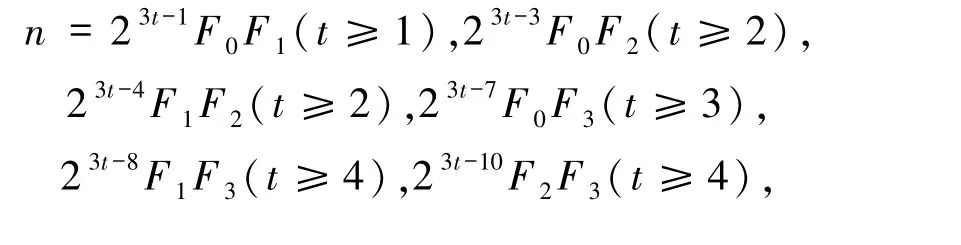
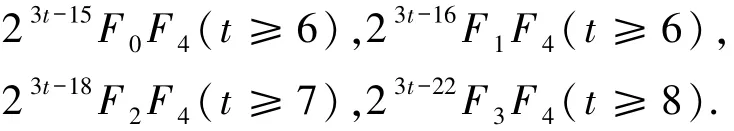
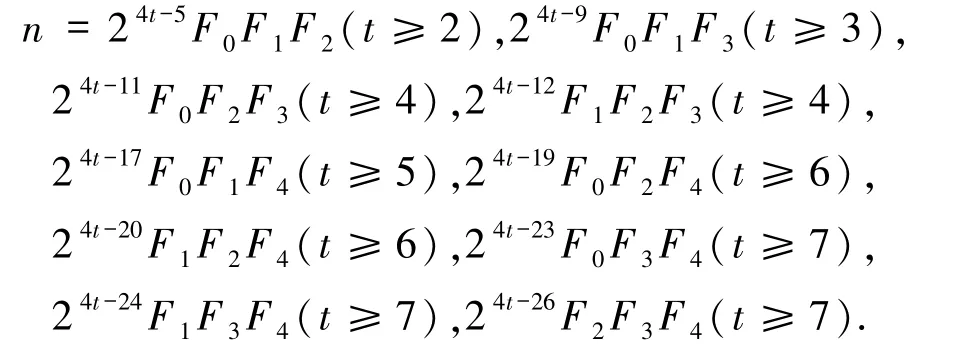
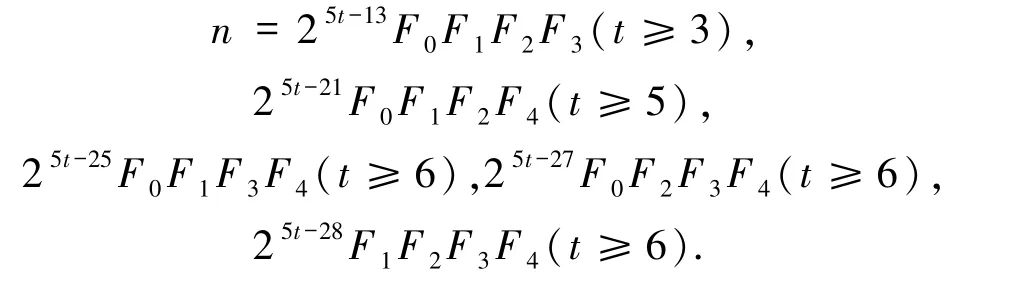
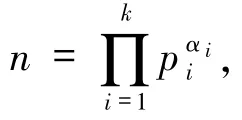
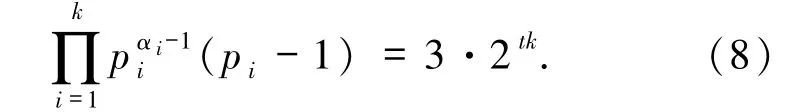
不妨设p1≡1(mod 3),则由(8)式知1 =2ui(2≤i≤k)且,故pi(2≤i≤k)为费马素数,p1为奇素数.由gcd(pi,3)=1 知pi∈{F1,F2,F3,F4}(2≤i≤k)且ui∈{2,4,8,16}(2≤i≤k),故
当k=1 时,n=p1,由(8)式知3·2a=3·2t,故a=t,从而
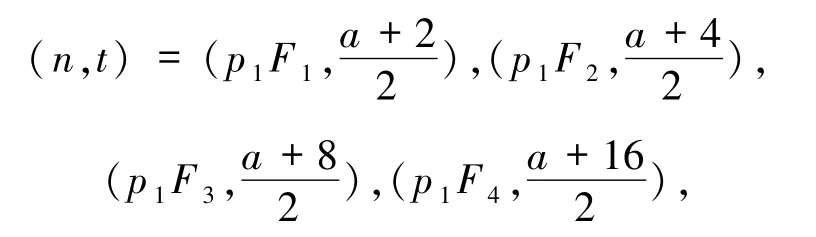
其中a≡0(mod 2).
类似可得k=3,4,5 时的方程(1)的解,证明过程类似k=2 的情形.
4)的证明类似3).
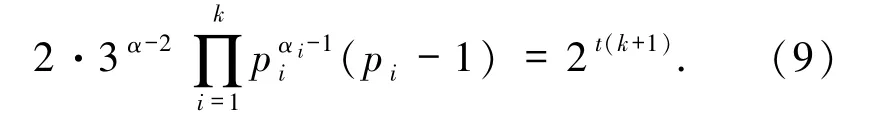
又由pi为奇素数且gcd(pi,3)=1,从而比较等式(9)两边2 的个数,可得α=2且(1≤i≤k),故,其中pi(1≤i≤k)为费马素数.又gcd(pi,3)=1,故F4},从而可得k≤4,且ui∈{2,4,8,16}(1≤i≤k),故由(9)式可得即
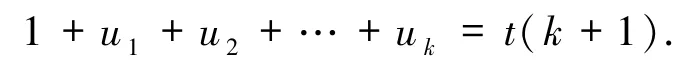
当k =1 时,n =9p1,且,故由u1∈{2,4,8,16}知2t∈{3,5,9,17},再由t∈Z+知方程(1)无解.
类似可得:
当k=2 时,n=9p1p2且,故(n,t)=(9F2F4,7).
当k=3 时,n =9p1p2p3且4t,故由t∈Z+知方程(1)无解.
当k=4 时,n=9p1p2p3p4且故由t∈Z+知方程(1)无解.
5 小结
本文基于φe(n)(e =2,3,4,6)的准确计算公式,利用初等的方法和技巧,对n进行分类讨论,研究了φe(n)=2tω(n)(e=2,3,4,6)时的正整数解.对e=3,4,6 时n的其他分类情况,在解决高次丢番图方程的基础上可进一步研究e =3,4,6 时n 的其他分类情况,例如:定理1.3 中对于方程(4),当k≥2时,方程
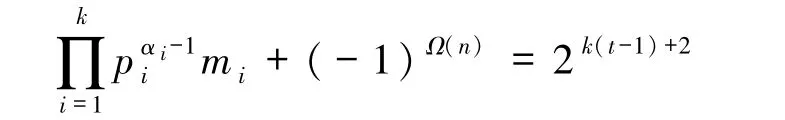
可解,本文其他未讨论的情况都可进一步研究.
附录

表1 定理1.1 的解(1≤k≤5)Tab.1 The solutions of Theorem 1.1(1≤k≤5)

表1 (续)
其中,
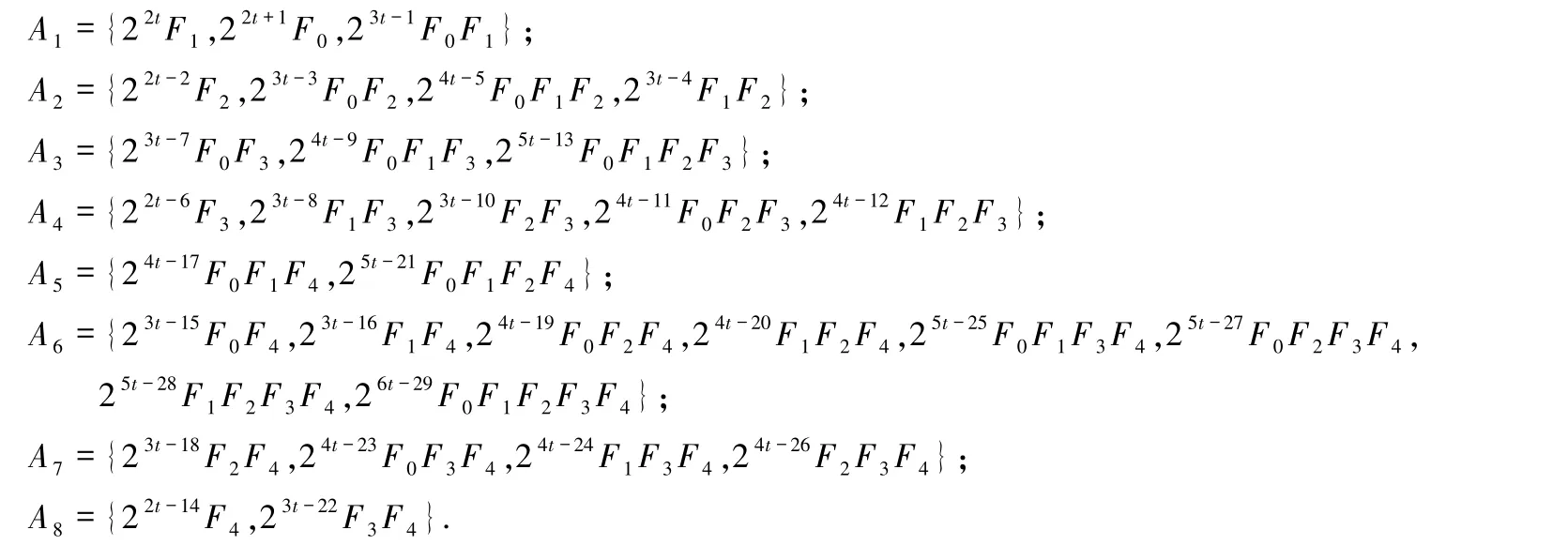

表2 定理1.2 的解(1≤k≤5)Tab.2 The solutions of Theorem 1.2(1≤k≤5)

表2 (续)

表3 定理1.3 的解(1≤k≤5)Tab.3 The solutions of Theorem 1.3(1≤k≤5)

表3 (续)
其中,
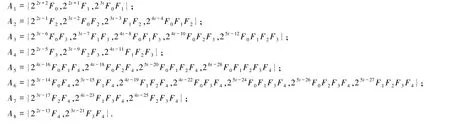

表4 定理1.4 的解(1≤k≤5)Tab.4 The solutions of Theorem 1.4(1≤k≤5)

表4 (续)

表4 (续)

表4 (续)
