基于模糊神经网络PID控制的粉体包装计量控制系统
2020-03-06王志山李昆祥徐雪萌
王 艳 陈 静 王志山 李昆祥 徐 芸 徐雪萌
(河南工业大学,河南 郑州 450001)
在包装计量过程中,计量精度一直是备受关注的关键因素,控制系统响应速度的快慢,超调量的大小,还有系统的稳定性直接影响着计量包装精度是否精确,因此对于控制系统的研究是目前提高包装计量精度的重要研究领域。就当前情况而言,中国的定量称重技术相较于国外还存在着一定的差距,虽然近20年中国定量称重包装设备的自动化程度有了很大的提升,但是由于中国研究起步晚,技术储备不足等因素导致设备开发相对较少,计量精度也不高[1-2]。
目前粉体包装计量控制通常采用PID控制,PID控制是一种采样控制,先通过对偏差值进行采样后再对控制量进行控制。PID控制由于结构简单、使用方便等优点,在各种控制生产中被广泛应用[3-5]。传统的PID控制是根据经验预先设定3个参数来实现闭环反馈控制[6]45,所以传统的PID控制只能用于线性的、静态的和控制精度要求不高的场合。而包装计量控制具有非线性、动态特性等[7-8]特点,传统的PID控制就不能满足其动态计量包装的要求。
BP算法是利用输出层得到误差估计出前一层(隐含层)的误差,再用此误差估计出更前层的误差,以此类推,可以获得隐含层中各层的误差,而且在由后向前的估算中也对权系数进行调整,使误差信号趋于最小[9]227。模糊神经网络PID能实现3个参数的实时在线调整,克服控制系统中的非线性和不稳定性[9]227-228,从而优化定量计量系统。
为了改善现有包装计量控制系统的不足,实现包装计量控制系统的实时在线控制,解决传统PID控制中不能改善的非线性和生产中系统动态与静态之间的矛盾[6]1-2的问题,试验拟设计基于模糊神经PID控制的粉体包装计量控制系统。
1 粉体计量包装控制的传统PID控制
研究的粉体计量规格为25 kg/袋,允许误差为±0.2%,主要装置如图1所示。粉体包装计量秤的工作原理是粉体物料进入加料仓即缓冲料仓后进行螺旋加料,当物料到达称重装置上的包装袋,称重装置会将称量值反馈给控制系统,控制根据传回的称量值来实时调节伺服电机的转速来改变加料速度,从而保证动态包装的精度[10]。传统的PID控制是根据粉体包装计量过程中实际称量值与设定称量值之间的偏差,来整定控制器中的P、I和D3个控制参数,从而调整螺杆喂料器的转速,传统的包装计量PID控制系统数学表达式为[2]:
(1)
式中:
U(t)——控制器的输出值;
S——控制器的比例系数;
I——积分时间,s;
D——微分时间,s。
其拉普拉斯变换后函数形式为:
(2)
式中:
G(s)——传递函数;
K——放大系数;
S——时间常数,s。
理想状况下,系统会将实际的称量值与设定的称量值比较从而得出偏差,利用偏差的大小来控制螺杆喂料电机的转速,理论上是一个线性控制过程。但在实际动态包装计量中由于零点漂移、落料冲击等干扰的存在,其控制系统是典型的非线性的系统。传统的PID控制,参数需提前设置,当系统误差发生变化时,参数不能根据误差的变化进行实时调整,不能很好地解决计量系统动态和静态性能之间的矛盾[6]1-3。因此采取模糊神经网络和PID控制结合的方法进行动态计量系统控制器的设计。

1. 托袋装置 2. 称重装置 3. 涨袋装置 4. 螺杆 5. 伺服电机 6. 呼吸帽 7. 蝶阀 8. 缓冲仓图1 粉体包装计量秤Figure 1 Powder packaging weighing scale
2 模糊神经网络PID控制系统
粉体包装计量控制系统不是一个线性的控制系统,且易受其他因素的影响。而模糊控制能较好地适应系统的非线性和时变性[11]。神经网络对环境的变化具有很强的自学习能力,而模糊神经网络控制器将模糊理论表达知识的能力与神经网络的自学习能力相结合,能提高系统的整体控制能力[9]228,且控制系统能够得到优化。
目前,BP神经网络的应用最为广泛,且是采用误差反向传播学习算法的多层前馈神经网络,多应用在系统辨识、自适应控制等领域[9]227。试验采用BP神经网络控制器,控制系统框图如图2所示。

图2 模糊神经网络PID控制框图Figure 2 Fuzzy neural PID control block diagram
2.1 模糊化模块设计
将实际值对比给定值得到偏差。模糊化得到模糊语言集合e。由模糊规则对e和模糊控制规则R根据进行模糊决策,得出模糊控制量U。
试验设计的是一个2输入、3输出的模糊神经网络PID控制器。输入为偏差与偏差变化率,利用模糊规则对P,I,D参数在线调整。以修正量△Kp,△Ki,△Kd作为输出,以应对PID参数在偏差和偏差变化率发生实时改变的情况下达到实时参数整定的需求,从而实现对包装计量的实时控制。
其中设定e,ec=[-6、-4、-2、0,2、4、6]。设其模糊子集为[NB、NM、NS、ZO、PS、PM、PB]。在选择隶属度函数时,由于三角形隶属度函数较为简单且运算方便,因此试验采用三角形隶属度函数,具体见图3。
基于PID参数经验,总结计量系统中的实际变化规律,得出模糊PID控制器Kp,Ki,Kd3个参数的控制规则表,见表1。
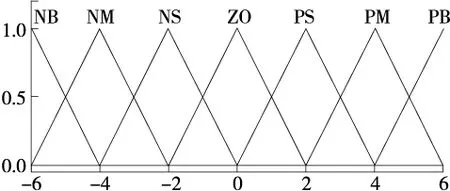
图3 e,ec隶属度函数图Figure 3 e, ec Membership function graph

表1 Kp,Ki,Kd的模糊控制规则表Table 1 Kp, Ki, Kd fuzzy control rules
2.2 粉体动态计量模糊神经网络PID控制器的设计
优良的动态包装系统包装精度误差值很小,与BP神经网络方法的训练目的是一致的。试验选取BP神经网络为学习算法。在BP神经网络中:第1层为两个输入即e和ec。第2层为7个神经元,分别对应输入的7个模糊子集NB,NM,NS,ZO,PS,PM,PB,第3层隐含层的神经元为49个,对应模糊PID控制器的49条规则。第4层隐含层的神经元个数为7,对应输出为相同个数的模糊子集。输出层分别是Kp,Ki,Kd。结构如图4所示。

图4 模糊神经网络系统结构图Figure 4 Structure diagram of fuzzy neural network system
网络结构中:
网络输入层的输入为:
(3)
式中:
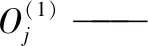
X(j)——输入层函数(j=1,2,表示两个输入e和ec)。
网络隐含层的输入、输出为:
(4)
式中:
wij——隐含层加权系数;
(1)/(2)——输入层/隐含层;
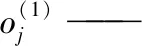
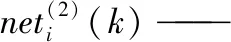

f——隐含层输出函数;
M——输入节点数。
隐含层神经元的激活函数为:
(5)
式中:
f(x)——激活函数;
x——输入值。
网络输出层的输入、输出为:
(6)
式中:
(3)——输出层;
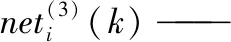
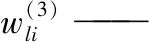

Q——隐含层节点数;
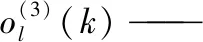
l——3个输出;
g——输出函数;

Kp/Ki/Kd——PID的3个可调参数。
由于Kp、Ki、Kd不能为负值,故输出层取正的Sigmoid函数,即
(7)
式中:
x——输入值。
性能指标函数为:
(8)
式中:
E(k)——输出层性能指标函数;
rin(k)-yout(k)——计算时刻误差;
rin(k)——给定值;
yout(k)——实际输出值。
修正权系数运用梯度下降法,附加一个惯性项为:
(9)
式中:

E(k)——输出层性能指标函数;
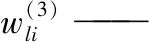
η——学习速率;
α——惯性系数。
经BP网络对模糊规则表的训练,得出输入到输出之间的非线性关系,从而获得网络各层神经元的连接权值和阈值,并确定输入与输出间的非线性函数。利用这种映射关系可以得出动态称量系统在任意e、ec的改变情况下Kp、Ki、Kd的修正值,实现实时在线控制。
3 模糊神经网络PID控制系统模拟仿真
参考文献[2]的近似数学模型:
(10)
式中:
G(s)——传递函数;
0.000 26——放大系数;
0.06/0.3/0.73——时间常数,s。
在MATLAB simulink仿真时[12-13],PID的3个初始值由临界比例度法来确定,在设置模糊神经网络PID控制参数初始值时与传统的PID初始参数一致,仿真结果如图5所示。
由图5可知,在两种PID控制系统中,模糊神经网络PID控制系统相对于传统PID系统稳定的时间提高了约45%,超调量减少了约16%。在开始时间段可以看出模糊神经网络PID控制系统也有一定的超调量。观察其传统的PID控制方法其超调量明显减小,而且系统达到稳定的时间相对较短。由此可知动态包装系统得到了优化,包装精度就会有所提升。同时,模糊神经网络PID控制器品质是否优良与初始参数、训练方法、模糊规则等因素有着至关重要的作用。试验中提到的模糊规则是借鉴前人的总结,运用的是BP神经网络,初始参数由临界比例度法得出。应该会有更适合的模糊规则、训练方法、模糊规则等因素使得系统能达到更优。
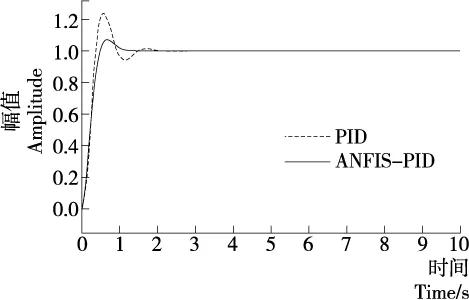
图5 系统的阶跃响应曲线Figure 5 Stepwise response curve of the system
4 结语
针对粉体包装计量控制系统受螺杆的旋转惯性、零点漂移,下料冲击力等因素的影响而造成的系统的延迟、非线性等问题,在传统PID的基础上增加了模糊神经网络智能控制方法,基于BP神经网络,PID的初始参数由临界比例度法得出,形成模糊神经网络PID控制器。由仿真系统的阶跃响应曲线图得知结果,与传统粉体动态包装计量控制系统相比,模糊神经网络PID控制系统稳定时间能缩短约45%,超调量约减少16%。这主要是因为模糊神经网络PID控制系统能实时调节PID的3个控制参数,从而使得控制系统得到优化。
