连续逆流提取黄芪多糖过程扩散返混数值模型的构建及单元化验证

毛琳璐 孙朋垚 张 霞,2 李 琳,2, 李玉婷 梁 毅 李 冰,2

(1. 华南理工大学食品科学与工程学院，广东 广州 510640；2. 广东省天然产物绿色加工与产品安全重点实验室，广东 广州 510640；3. 东莞理工学院，广东 东莞 523000；4. 广东中轻枫泰生化科技有限公司，广东 茂名 525427)

天然产物有效成分的提取过程是中成类药物制剂的核心单元之一。在多种提取方式中，连续逆流提取(CCE)技术因其独特的两相接触方式，在实现连续化生产的同时，能保证足够的浓度差推动力，因而备受关注。目前已开发出各种构型的连续逆流提取器。其中使用最广泛的是单螺旋推进型连续逆流提取器，多数研究[1-3]均在此基础上展开，包括提取空间内的结构设计、流动场布置、截面改进等。但随着现代科技尤其是分离技术的发展，对连续逆流提取过程可控性的要求也日渐提高，建立严格统一的数学理论模型，实现对连续逆流提取流程浓度分布描述，对产品质量控制和装备智能化水平提升意义重大。

目前，用于描述连续逆流提取过程的数学模型分为以下几类：① 平推流扩散模型[4]。这类模型大多将提取空间看作近似一维，在截面方向上将所有流动类型作为平推流处理，而平推流扩散模型具有很大的局限性，在径向浓度分布极差较大的高黏度溶剂提取操作中，仅仅用平均线速度代替整体流动是很难准确描述的。② 轴向扩散整体传质模型[5]。基于总传质系数和轴向扩散的整体传质模型，该模型已成功应用于许多饮料加工、液体原料包装等食品加工环节[6]，而该模型并没有直接结合物料的基本性质(如固体内部扩散性)。传热对扩散过程初始阶段结构变化的影响，尤其是在植物组织作为提取对象的情况下，植物细胞的浸润和质壁分离过程并没有考虑。③ 经验化模型[7]与特征函数模型[8]。这类建模方法的主要特点是通过具体的提取试验来减少建模的复杂性，进而估计与质量传递相关的固体特性。但无法直接与深入解释固体内部发生的扩散机制对整体传质的影响，并不适合于工艺优化，而且根据不同的研究结果总结出的经验模型差异很大。④ 弥散扩散模型[9]。此模型是目前针对生物组织提取研究开发的较为全面的模型，结合了非稳态扩散理论和稳态/非稳态反混理论，同时考虑固相内部结构不均匀性和复杂的界面条件随时间与位置的变化情况，但需要先进的计算机技术与极其密集的数值化运算对模型内的全部变量完成部署，对于模型中高动态域部分的解析与开发仍需进一步探究。

针对弥散扩散模型内变量复杂、计算量庞大的缺点，试验拟提出一种简化的扩散返混模型，用于描述实验室规模到中试规模的单流程连续逆流提取器内的浓度分布，将提取过程中浓度的变化归结为多项关键传质参数的数值变化，提升模型的普适性。建模后，在实验室规模的不同提取条件下进行单元化连续逆流提取黄芪多糖对数值模型进行验证，计算模型输出值与实际值的平均相对误差，从而验证模型的有效性及准确性，为连续逆流提取设备的设计优化提供理论依据。

1 材料与方法

1.1 材料与仪器

1.1.1 材料与试剂

蒙古黄芪干燥根(饮片)：产自甘肃省定西市陇西县；

蒙古黄芪干燥粉：实验室自制，过10目筛；

纤维素酶(绿色木酶)：>25 U/mg，上海源叶生物科技有限公司；

果胶酶：>50 U/mg，上海沪试实验室器材股份有限公司；

木瓜蛋白酶：>800 U/mg，上海源叶生物科技有限公司。

1.1.2 仪器与设备

万分之一天平：BS224S型，赛多利斯仪器系统有限公司；

高速粉碎机：BMF-6BI型，济南倍力粉技术工程有限公司；

高速冷冻离心机：30KS型，德国Sigma公司；

紫外—可见分光光度计：UV2600型，美国Varian仪器公司；

循环水式多用真空泵：SHZ-D(III) 型，上海秋佐科学仪器有限公司；

数显恒温水浴锅：HH-4型，常州澳华仪器有限公司。

1.2 连续逆流提取扩散返混数值模型的构建

数值模型中连续逆流过程的分割大致分为两类：按线性流动分割和按体积流动分割。而中试规模以上的提取空间内流体流动速度是随空间内的位置而变化的，因此采用恒定体积流动的分割方式使得计算更为准确，模型开发与分析更为简化。为了在后续研究中开发连续逆流提取扩散返混模型，对真实的提取过程作出假设：

① 溶质在固相和液相内的平衡分布系数恒定；

② 固体物质内部传质阻力均匀且尺寸恒定(可用平均尺寸替代)；

③ 提取过程达到稳态后，物料已完全浸润，表面洗涤效果忽略不计；

④ 固体物料的体积流量恒定；

⑤ 提取溶剂和被提取物料均不可压缩，当输入流量变化时，提取空间内各处液相与固相的体积流量也会瞬间发生变化。

另外，相比于上述所提到的各种建模方式，试验模型的构建过程中并没有限定溶质扩散系数或总传质系数保持恒定。在提取空间内随着位置的变化，溶质扩散返混程度随溶质浓度、流速与耦合物理场的变化而变化，更接近于真实的工业化连续逆流提取。

1.2.1 微元溶质守恒方程 对连续逆流提取空间的总体物料及所取微元内物料进行衡算，如图1所示。

在连续逆流传质过程中取与流动方向垂直的一微元dv为研究对象，dv内包含固相微元dvx和液相微元dvy，其中Dx、Dy随vx、vy而变化。

考虑微元中的固相，取固相流动方向为正方向，该微元左侧的溶质传递量T0为固相流动所引起的对流传质量与固相浓度差引起的扩散传质量(符合Fick第二定律)两部分组成，即：

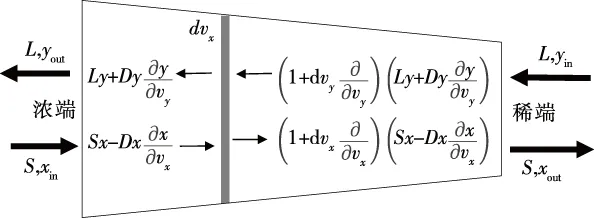
图1 连续逆流提取空间内的总体及微元物料守恒模型Figure 1 Schematic view of material balance for differential volume along the CCE unit

(1)

将该处的传质量当作vx的函数，则在vx+dvx处的传质量Tx为：

(2)

整理后做线性近似可得：

(3)

根据固相微元内的溶质质量守恒可知，溶质由固相转移到液相的溶质流速为0，即：

(4)

式中：

S——固相体积流量，m3/s；

L——液相体积流量，m3/s；

x——固相中溶质质量分数，kg/m3；

y——液相中溶质质量分数，kg/m3；

vx——从固相入口处至微元处的固相累计体积，m3；

vy——从液相入口处至微元处的液相累计体积，m3；

Dx——固相内扩散系数，m6/s；

Dy——液相内扩散系数，m6/s；

Ks——微元内固液总传质系数(随vx、vy而变化)，m6/s；

dA——微元内固液传质面积，m2；

x*——平衡时溶质在固相中平均浓度，g/g。

将式(4)整理后可得固相溶质平衡方程：

(5)

同理，对液相微元dvy进行推导，可得液相溶质平衡方程：

(6)

式(5)、(6)同时考虑了3项引起微元内溶质质量变化的因素，即流体流动引起的对流传质、同相浓度差引起的扩散传质以及两相浓度差引起的固液传质，使得后续建模过程更贴近实际工作状态，建模结果更准确。

1.2.2 边界微元溶质守恒方程 在传质过程的最左(右)侧取一微元计算，由于不存在比该微元浓度更高(低)的区域，微元左(右)侧的扩散传质项为零，仅有对流传质项；而在右(左)侧同时存在两项；由于微元处于液相或固相入口处，可认为该微元内的固相或液相浓度保持恒定，则有：

(7)

(8)

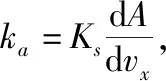
(9)

令Ts=τka，可得到固相无量纲化的固相物料平衡方程：

(10)

式中：

m——分配系数。

同理，令ν=L/S=vy/vx，表示液相与固相体积比；R=∀xL/Dy，从而使∀x、L、Dy合并为一个无量纲系数即液相中的佩克莱数，用来表示液相中的对流与扩散相对比例；令TL=TSS/L；代入液相平衡方程，得无量纲化液相物料平衡方程：

(11)

此外，将以上参数代入边界溶质平衡中，得无量纲化边界物料平衡方程：

(12)

(13)

(14)

(15)

1.2.4 方程的有限差分变形 使用一阶差商代替一阶导数项，二阶差商代替二阶导数项，即：

(16)

(17)

(18)

(19)

其中xi、yi分别表示在位置z=iΔz处的固相、液相浓度，将式(16)～(19)代入连续逆流传质过程固相微元溶质守恒方程：

E1,ixi-1+E2,ixi+E3,ixi+1+E4,iyi=0，

(20)

E1,i=2-PiΓiΔz，

(21)

E2,i=-(4+2PiTs,iΔz2)，

(22)

E3,i=2+PiΓiΔz，

(23)

(24)

将差商代入连续逆流传质过程液相微元溶质守恒方程：

E5,iyi-1+E6,iyi+E7,iyi+1+E8,ixi=0，

(25)

E5,i=2-νRiΨiΔz，

(26)

(27)

E7,i=2+νRiΨiΔz，

(28)

E8,i=2νRiTLiΔz2，

(29)

(30)

将差商代入连续逆流传质过程边界微元溶质守恒方程：

x-1=2P0Δz(xin-x0)+x1。

(31)

其中，y-1=y1；xn+2=xn。

yn+2=2νRn+1Δz(yin-yn+1)+yn。

(32)

其中，xout=xn+1；yout=y0。

1.2.5 溶质守恒矩阵形式求解 将式(20)、(25)展开成矩阵形式：

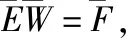
(33)

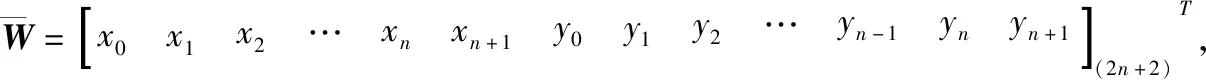
(34)

(35)

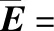
(36)

其中，G=E2,0-2E1,0P0Δz；H=E1,0+E3,0；I=E1,n+1-E3,n+1；J=E5,0+E7,0；K=E5,n+1+E7,n+1；L=E6,n+1-2νRn+1E7,n+1Δz。

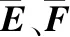
数据输入：固液比(α)，平衡分配系数(m)，固体(xin)和液相(yin)的入口溶质浓度，固相流速(S)，固相停留时间(τ)，固体(P)和液相(R)中的佩克莱数，总传质系数TL、TS，两相内扩散系数Dx、Dy，连续逆流提取的分割数(n)和单元长度(Δz)。

1.3 单元化连续逆流提取黄芪活性多糖

1.3.1 不同温度下的模拟连续逆流提取 根据谢红旗等[10-11]的方法，修改如下：搭建模拟连续逆流提取装置(图2)，提取单元依次编号1～10，水浴加热调节提取单元温度为40，50，60，70 ℃，在单元1内放入5.0 g黄芪干粗粉，单元提取时间为总提取时间的1/10，以金属滤布阻隔完成快速过滤，加入下一提取单元，完成最后一个单元的提取后，依次测量以上各单元的提取液多糖浓度并记录。保留提取后残渣并编号；舍弃单元1内提取液，将单元2～10依次向前移动至单元1～9的位置，在单元10位置补充新鲜提取溶剂(pH 9.0)，重新将单元标号1～10，重复各单元提取步骤直至完成10次移动。提取期间对各单元进行蒸馏水量补充确保固液比恒定。

图2 模拟多效连续逆流提取黄芪多糖试验装置示意图Figure 2 Simulation of multi-effect CCE of APS test device

1.3.2 不同固液比的模拟连续逆流提取 改变每个单元内的固液比为1∶6，1∶8，1∶10，1∶12，1∶14 (g/mL)，重复1.3.1的操作。

1.3.3 不同单元提取时间的模拟连续逆流提取 改变每单元提取时间为4，5，6，7 min，重复1.3.1的操作。

1.3.4 提取液中总糖及还原糖含量测定 分别按GB/T 15672—2009和GB 5009.7—2016执行。

1.3.5 数据统计与分析 所有试验均重复3次，采用SPSS 22.0软件进行统计分析，应用ANOVA进行显著性分析(P<0.05)。结果以(平均值±标准差)表示。应用Origin 2018C软件作图。

1.4 连续逆流提取扩散返混数值模型的单元化验证

1.4.1 固液比 在实际的植物根茎类天然产物提取过程中，特别是对大分子有效成分的提取，固液比大多控制在1∶6～1∶14 (g/mL)，过低的固液比会导致提取效率低下，而高于1∶14 (g/mL)的固液比会导致提取液过度稀释，增加后续浓缩成本。此时提取温度50 ℃，总提取时间50 min。

1.4.2 提取温度 提取温度虽未作为一项参数纳入模型的数值计算中，但该模型的一些主要体现传质强度的参数如Dx与Dy、P与R、TL与TS等可能会受到温度的影响，根据1.3静态提取条件优化试验(数据未显示)，较为合适的提取温度为40～80 ℃，因此将此范围的实际提取数据作为模型的验证样本。此时固液比1∶10 (g/mL)，总提取时间50 min。

1.4.3 总提取时间 根据1.3静态提取条件优化试验(数据未显示)，较为合适的提取时间为40～70 min，因此将此范围的实际提取数据作为模型的验证样本。此时提取温度50 ℃，固液比1∶10 (g/mL)。

1.4.4 模型预测浓度与实际提取样本浓度的平均相对误差 按式(37)进行计算。

(37)

式中：

ε——平均相对误差，%；

i——提取单元编号；

j——扩散返混模型微元编号；

wi——实际提取测试样本中第i单元内提取液的多糖浓度，g/m3；

由于模型中的单元分割数不一定为实际提取单元数10，所以在检验模型前先将n个提取微元映射到10个提取单元内，即j/n=i/10。

2 结果与分析

2.1 不同固液比下提取样本对模型的验证

由图3可知，随着固液比的增加，提取液中多糖浓度出现明显的浓端推移，固相中残留物与初始溶质浓度比值下降更快，出口处渐近浓度降低。这是由于固液比影响了液相本体与固相本体的浓度差即传质推动力，在前几单元多糖已基本溶出。

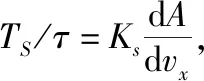
2.2 不同提取温度下提取样本对模型的验证

由图4可知，随着提取温度的升高，提取液中多糖浓度出现明显的浓端推移，液相中多糖浓度溶出速度更快，出口处渐近浓度降低更快。以单元内多糖残留量<100 mg 为提取终止浓度分界线，提取温度为40，50，60，70，80 ℃时的终止单元分别为第9，第8，第7，第6，第6单元。这是由于提取温度影响了溶质在两相内的热运动，集中降低了液膜与固膜传质阻力，导致在前几单元便完成了大部分的多糖溶出。

由表2可知，当提取温度为40，50，60，70，80 ℃时，平均相对误差分别为3.17%，4.96%，5.57%，9.16%，11.47%；TL与TS、Dx与Dy随提取温度的升高而增大，佩克莱数P与R随提取温度的升高而减小。

图3 固液比对多糖含量的影响及数值模型拟合Figure 3 Effect of solid-liquid ratios on polysaccharide content and numerical model fitting

表1 不同固液比下数值模型参数拟合结果Table 1 Numerical model parameter fitting results under different solid-liquid ratios

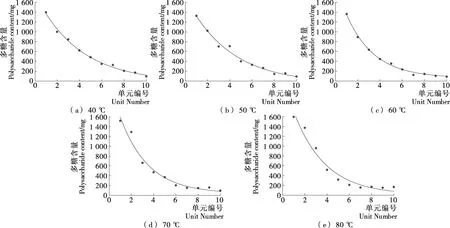
图4 提取温度对多糖含量的影响及数值模型拟合Figure 4 Effect of extraction temperature on polysaccharide content and numerical model fitting

表2 不同提取温度下数值模型参数拟合结果Table 2 Numerical model parameter fitting results under different extraction temperature

2.3 不同提取时间下提取样本对模型的验证

由图5可知，随着提取时间的延长，提取液中多糖浓度分布明显向浓端单元移动，总提取时间的延长使单元内提取时间延长，降低单元内平均浓度差推动力。

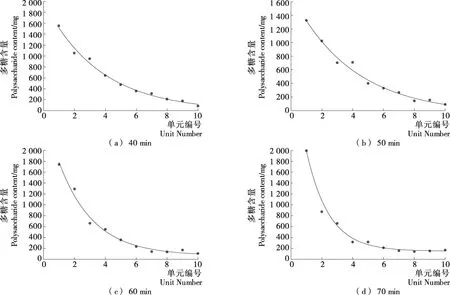
图5 提取时间对多糖含量的影响及数值模型拟合Figure 5 Effect of extraction time on polysaccharide content and numerical model fitting

表3 不同提取时间下数值模型参数拟合结果Table 3 Numerical model parameter fitting results under different extraction temperature

3 结论

试验构建了适用于单流程连续逆流提取器的稳态浓度分布数值模型，该模型同时考虑了扩散传质、对流传质以及界面传质3种效应对连续逆流提取黄芪多糖过程的贡献，并作了定量化的数学关系构建。在模型的数值求解过程中，采用具有二阶误差的中心差分公式，转化为矩阵形式，借由计算机软件Matlab R2016a编程执行计算得到预测浓度分布。此外，使用单元化连续逆流提取的试验数据验证了该模型，结果表明，在单因素的变化范围内，模型预测分布和实际提取样本浓度的相对误差均控制在15%以内，表明该模型可成功用于描述提取过程的传输现象，具有应用价值，并且是连续逆流提取达到稳态条件下的适用预测工具。

在描述多种生物原料及复配提取溶剂的提取过程时，需要充分表征两相内部和固液两相边界处的传质条件，即模型中的关键参数接口TL与TS，Dx与Dy以及P与R，分别代表两相体积总传质系数、两相扩散系数以及两相佩克莱数(用于表示扩散传质和对流传质的相对强度)。而影响这些参数变化的因素多种多样，而且没有统一的理论指导，因此并不适合放入数值模型中一并计算，而是以待定参数的形式暂时补全模型。后续可进行单独或独立的研究，以便将提取条件和溶质的表观扩散性相关联，使扩散返混模型足够灵活，满足大多数工业和研究建模需求。