拉普拉斯逼近方法在复杂函数积分中的应用∗

郑良芳，胡锡健

(新疆大学数学与系统科学学院，新疆乌鲁木齐830046)

0 引言

近年来，在人工智能，机器学习等众多领域中，贝叶斯统计方法得到了广泛的应用和快速发展，同时也面临着多方面的挑战.众所周知，贝叶斯统计应用的瓶颈在于复杂函数积分及高维积分的计算.大部分可积函数的积分无法用初等函数表示，或是无法有解析表达式.因此，对积分的近似计算就显得尤为重要.20世纪90年代，马尔科夫链蒙特卡洛(MCMC)思想被引入到贝叶斯推断中，使得(理论上)可以通过生成平稳随机数，计算任何想要得到的统计推断结果，这已成为研究大量复杂问题的主流手段[1].然而，应用MCMC方法估计模型的参数，由于其多种迭代抽样往往需要大量的时间，且精度不高，收敛速度较慢.

拉普拉斯逼近方法[2]是一种积分逼近技术，适用于被积函数存在(陡增的)最大值情形.如果被积函数满足单峰，对称性和轻尾行为等相关属性，则收敛速度更快[3].由于拉普拉斯逼近方法计算速度快，逼近精度高，使得其在积分逼近的应用中深受研究者们青睐.在贝叶斯统计中，文献[4]认为拉普拉斯逼近方法对于后验分布和边际密度的逼近都是比较精确的，在线性混合效应模型中，拉普拉斯逼近方法的使用最为广泛，也可能是唯一能在实际中使用的方法[5].许多研究者将拉普拉斯逼近方法应用于一些实际问题之中，如Lastly等[6]将拉普拉斯逼近方法用于生存分析，Ruli等[7]基于拉普拉斯逼近方法提出了一些新的算法，应用于贝叶斯统计的应用中.

本文将拉普拉斯逼近方法用于复杂函数积分的近似计算中.文章介绍了拉普拉斯逼近方法的主要应用公式以及应用思路，然后将其应用于几类复杂函数积分的计算，并通过实例分析可知拉普拉斯逼近方法近似计算的效果比较满意，逼近精度也较高.

1 拉普拉斯积分逼近方法

在被积函数为单峰时，可以使用拉普拉斯逼近方法对这类函数积分近似计算，且确保拉普拉斯逼近方法近似收敛到一个唯一的最大值[8].由于泰勒公式让我们可以通过一个点来窥视整个函数的发展，因此，拉普拉斯逼近方法通过对被积函数在众数点的泰勒展开对所求被积函数近似计算.由韦来生等[9]对后验分布的渐进正态性的证明可知对数似然函数的三阶导数项及更高阶项是可以忽略的.因此在使用泰勒展开时，我们通常只考虑展开到二阶导数项.

若有如下形式的积分:

其中函数f(θ)是θ的光滑函数且函数f(θ)存在唯一最大值点点可以认为是极大似然估计值或者是后验众数.如果f 在点有唯一的最大值，则积分I 的绝大部分的贡献都来自于的邻域上的积分.在一些具体场合下，nf(θ)可以表示对数似然函数或者没有正则化的后验密度f(x|θ)π(θ) 的对数.

一般地，对p维参数θ，可以得到：

由上述过程可知，使用拉普拉斯逼近方法的大致步骤如下:

Step1: 将被积函数写成指数次幂的形式，并写出相应的对数形式；

Step2: 对对数形式下的函数求一阶导数，并令其一阶导数为0，从而得到相应的最大值，进而可得被积函数在最大值点处的表达形式；

Step3: 对对数形式下的函数求二阶导数，并由Step2中所得的最大值，可求得(2)式中c的值；

Step4: 将上述相关量代入(2)式中，可得被积函数的拉普拉斯近似逼近结果.

2 拉普拉斯逼近方法的应用

下面本文考虑将拉普拉斯逼近方法用于一些实际计算问题之中，并从这些实例分析中验证拉普拉斯逼近方法的优势所在.

在统计应用中，需要对多元变量和的密度函数进行计算.当变量间相互独立时，和的密度函数是显然的，而当变量不相互独立时，和的密度函数不易计算或是没有解析表达式.此时，可以通过拉普拉斯逼近方法近似计算.

例 1:假设并且X和Y 不独立，Z=X+Y.此时，我们采用拉普拉斯逼近方法来近似求解. Z的密度函数为:

令x=z −y, 则积分如下:

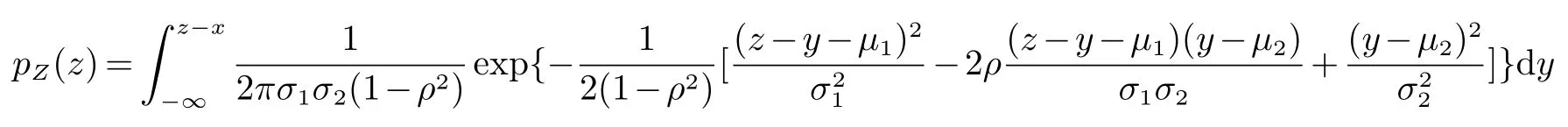
由(2)式可令

由拉普拉斯逼近步骤，令f(y)=0，得到

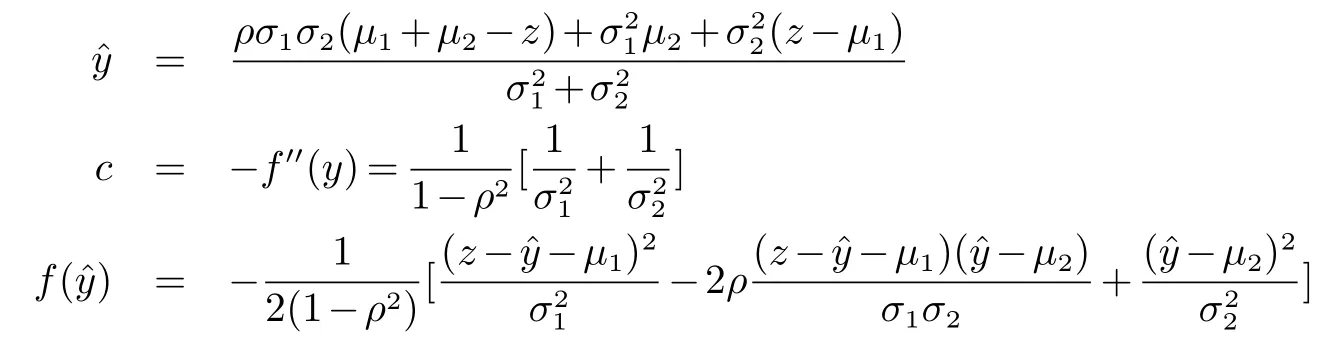
由公式(2)可得变量Z的密度函数如下:

2.1 拉普拉斯逼近方法对密度函数积分的逼近

设f(x)是随机变量X的概率密度函数(一般满足单峰性).在一些实际问题中，我们需要对其进行积分，但积分的结果往往不易求得.此时，我们可以通过拉普拉斯逼近将其转化为正态分布的形式，进而求得对一般分布积分的近似结果.类似公式(2)的推导有:

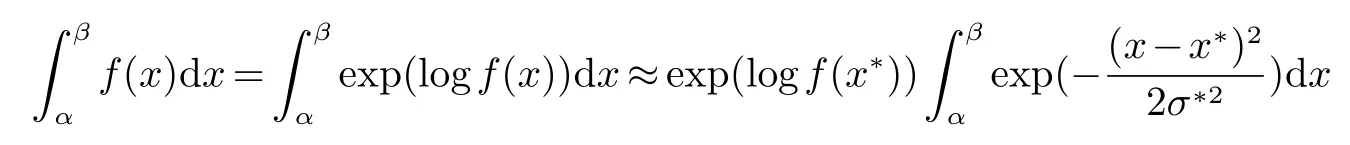
其中, σ∗2=−1/f(x∗),x∗为f(x)的极大值点.上式最右端的被积函数是正态分布N(x∗,σ∗2)的核，所以积分区域为(α,β)的积分近似为:

Ψ(·)是正态分布N(x∗,σ∗2)的分布函数.

例2:f(x)是伽马分布，求积分在不同参数(a,b)和不同积分区域(α,β)下的值.

对于该积分，常用的积分方法无法求解，而MCMC方法由于很难抽样，难以求解出近似结果.我们考虑用拉普拉斯逼近方法来近似求解.

伽马分布的密度函数:

其中x,a,b>0.对f(x)取对数为:

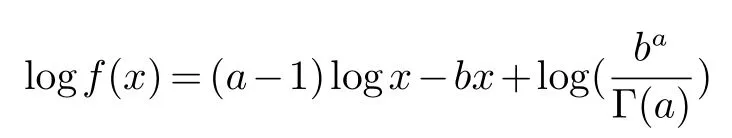
伽马分布的积分的拉普拉斯近似为:

其中Ψ(·)是正态分布N(x∗,σ∗2)的分布函数.表1给出不同参数和不同区间下的伽马分布以及相应的正态分布的积分值以及相应的均方误差（MSE），并通过R软件进行相关计算，利用R软件画出当a=5,b=1,α=1,β=10 时的伽马分布密度函数的图像以及所对应的正态分布的密度函数的图像.

表1 伽马分布在不同的参数a,b 以及不同积分区域(α,β)积分的精确值与近似值Tab 1 Gamma distribution with different parameters a,b and the exact value and approximation of the (α,β)integral for different integration regions

从表1中的数据可知，拉普拉斯逼近方法的结果与实际结果比较接近，并且当积分区域越接近众数，逼近精度也越高.图1也显示出被积函数的相应正态分布密度函数的逼近效果很好，尤其是在众数附近，正态分布的密度函数与伽马分布的密度函数非常贴近.表1和图1二者都显示出拉普拉斯逼近方法对密度函数积分计算的效果很好.因此，在对密度函数进行积分时，用拉普拉斯逼近方法近似得到结果是可行的.

2.2 拉普拉斯逼近方法对后验均值的逼近

在贝叶斯推断中常常需要计算如下形式的积分

其中f(x|θ)为似然函数，π(θ)为先验密度，g(θ)为θ的函数.后验分布的其他特征也可以表示为这种积分形式.

光滑函数g(θ)的后验均值

在贝叶斯推断中极其重要，下面我们推导它的近似计算公式.令L = logπ+logf,L∗= logπ+logf +logg,是L的后验众数，σ2= −1/L(θ).则用拉普拉斯方法得到近似为:

图1 a=5,b=1,α=1,β=10 时的伽马分布密度函数的图像以及所对应的正态分布的密度函数的图像Fig 1 An image of the gamma distribution density function at a=5,b=1,α =1,β =10 and an image of the density function of the corresponding normal distribution

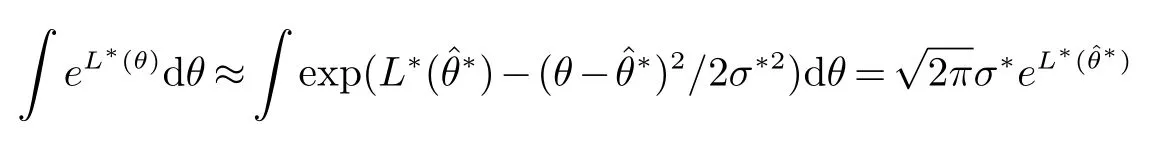
则后验分布的均值估计为:

多元变量的情形为:

2.3 拉普拉斯逼近方法对边际密度函数的近似逼近

Leonard[11]首次提出的结果中提供了一种有用的近似替代方法，而后Tierney[10]，Kass[12]以及Rue[13]都曾将拉普拉斯逼近方法广泛应用于后验密度的近似求解中.Friel和Wyse[14]综述了近似边际密度的不同方法.

对多维密度函数求解边际密度函数时，求解方法如下:

设函数p(X)为n维光滑函数且存在唯一最大值，X=(x1,x2,···,xn), 令H(X)=exp{p(X)}，则p(X) 可写为如下形式:

具体而言，边际密度p(x1)的拉普拉斯近似可由(3)式得出，其中分母的拉普拉斯近似为：

最后一个条件密度p(xn|X1:n−1)的拉普拉斯近似为:

对于(4)式中的其余边际条件密度可以此类推，从而可得在多元密度函数中，边际密度函数的拉普拉斯近似.

2.4 拉普拉斯逼近方法对卷积公式的逼近

拉普拉斯逼近方法还可用于对卷积函数的近似求解.卷积是一种积分变换的常用方法，在金融保险、信号系统、深度学习(卷积神经网络)、图像等方面有着极为广泛的应用.设函数f(x),g(x)是实数域R上的两个可积函数，作积分

可以证明关于所有的实数x，上述积分是存在的.随着x 的不同取值,上述积分定义了一个新的函数，记作h(x)=(f ∗g)(x)，称为函数f(x),g(x)的卷积.

例 3:设且X和Y 相互独立，证明

证明由题设可知，Z=X+Y 在(−∞,+∞)上取值，由卷积公式(5)可以得到：

直接使用拉普拉斯积分逼近公式(2)，此时由上面第一个等式可令

令f(y)=0, 解得

并且有

将上述部分带入到拉普拉斯积分逼近公式(2)中，则可以直接得到:

因此，使用拉普拉斯积分逼近方法可以快速得出结果.

3 结论

由上述推导过程及应用可知，使用拉普拉斯逼近方法时，被积函数f(x) 应满足拉普拉斯积分逼近方法的主要思想是对被积函数在最大值点进行泰勒展开(通常只考虑前两阶的导数)，并将被积函数转化为正态分布密度函数的形式，通过对相应的正态分布密度函数进行积分，从而求得被积函数的近似结果.

拉普拉斯方法还用于求解一些复杂问题，如高维积分的求解问题.通常这些问题都难以解决或是不容易解决，而使用拉普拉斯逼近方法通过对被积函数相应的正态分布密度函数进行积分（可查阅标准正态分布表），得到所求积分的近似结果，使得问题得以简化，计算更加快捷，同时还保持了较高的误差精度.通过上述公式推导以及实例分析可知，对满足一定条件的复杂函数积分以及在贝叶斯框架下统计量的近似计算，采用拉普拉斯逼近方法对其进行有效近似是合理的，并且也是十分有用的.

拉普拉斯逼近方法以其简洁的计算公式，快速的计算方法和其精确的近似结果，为统计推断的工作带来了极大的方便，也因此成为了统计工作者们所青睐的对象.并且作为Inte-grated Nested Laplace Approximations（INLA）[13]算法的核心，拉普拉斯逼近方法被广泛的应用于空间以及时空数据的处理，节约了大量的计算时间，大大的提高了工作效率.同时，由于INLA算法的广泛应用，拉普拉斯逼近方法也可用于如孙彬[15]对于大数据的处理之中.随着科学技术的发展进步和研究工作的深入，拉普拉斯逼近方法也将会被应用到更加广泛的领域之中.