基于GBRT模型的交通事故预测∗

杨文忠，张志豪，柴亚闯，温杰彬，杨蒙蒙，富雅玲

(新疆大学信息科学与工程学院，新疆乌鲁木齐830046)

0 引言

“到2020年，将道路交通事故造成的全球伤亡人数减半”是联合国（UN）2015年发布的可持续发展目标（SDG）之一[1].将交通事故态势预测结果应用到交通规划中，能提高交通安全水平.目前，对交通事故预测的研究方法主要有统计回归法[2]、灰色预测[3]和神经网络模型等三种.上述方法普遍存在预测精度低、鲁棒性低的问题.

回归预测的计算简单方便，但只是对数据进行了简单的线性拟合.文献[4]利用自回归综合移动平均线（ARIMA）和具有解释变量的自回归综合移动平均线（ARIMAX）建模技术，建立了尼日利亚阿南布拉州事故频率的预测模型.针对复杂的交通事故问题，回归预测可靠性低.

在样本数量少的情况下，灰色预测[5,6]可以对具有光滑的离散函数特性的数据建模进行预测.文献[7]提出了适用于具有较强指数规律的序列GM(1,1)模型对交通事故进行预测，但该模型只能描述单调的变化过程.文献[8]提出了道路交通事故灰色Verhulst预测模型，适用于非单调的摆动发展序列或具有饱和状态的S形序列.文献[9]提出了多种灰色预测方法的加权组合模型，通过加权组合的数学方法虽然能提高精度，但预测的含义变得模糊，且对中长期的预测能力不足.

神经网络预测法具有很强的自学习能力，可以构造出拟合能力很强的非线性映射.文献[10]通过使用BP 神经网络来构造交通事故预测模型.文献[11]对BP神经网络模型进行改进，结合灰色理论缩短了BP神经网络训练收敛时间.BP神经网络模型不足的是它收敛速度慢、训练时间长，训练时容易陷入鞍点，模型理论的可解释性差.

交通事故自身随机性大，一些研究方法中考虑加入数据的时序关系来提升预测精度，但是鲁棒性不高.文献[12]考虑了道路数据的时序关系，使用马尔可夫模型对交通事故建模，预测效果有所提升.但马尔可夫过程具有一些局限性，数据处理时只与上一时间步有关，与再之前的时间步无关.LSTM神经网络模型[13,14]能学习历史数据中存在的时间依赖关系进行预测.但实验结果中显示，当预测数据中出现与原来数据趋势相反的拐点数据时，预测误差会增大，LSTM模型存在鲁棒性不足的问题.针对这种情况，我们使用集成学习方法构建增强梯度回归树（GBRT）模型.GBRT模型能通过使用一些健壮的损失函数，来增强对异常值处理.各模型的对比实验结果显示，在相对少的调参情况下，GBRT预测误差最小，且训练时间比神经网络模型少很多.

1 增强梯度回归树模型

GBRT是一种boosting[15]类型的集成学习算法[16].集成学习是一种技术框架，它通过使用多个不同的基模型进行组合来完成相应的工作，以到达更加高效、准确的目的.目前常用的集成学习框架包括：bagging，boosting和stacking.其中boosting框架的训练过程为阶梯状，基模型按序训练，基模型的训练集按照汇总策略每次都进行一定的转化，随后将所有基模型的结果进行线性综合产生最终的预测结果.图1为boosting集成学习框架的示意图.

图1 boosting集成学习框架的示意图Fig 1 Diagram of the boosting ensemble learning framework

基于boosting框架的整体模型可以用线性组合来描述:

其中hi(x)为基模型与其权值的乘积.整体模型的训练目标是使预测值F(x)逼近真实值y，也就是说要让每一个基模型的预测值逼近各自要预测的部分真实值.利用训练实例对hi(x)进行测试，增加了错误分类实例的权重.研究者们想到了一个贪心的解决手段：每次只训练一个基模型，每一轮迭代中，只要集中解决一个基模型的训练问题.

通过引入任意损失函数，拟合反向梯度

GBRT是基函数使用树结构的boosting集成学习模型.对于给定的n条记录m个特征，使用K个树函数累加来预测输出.公式如下

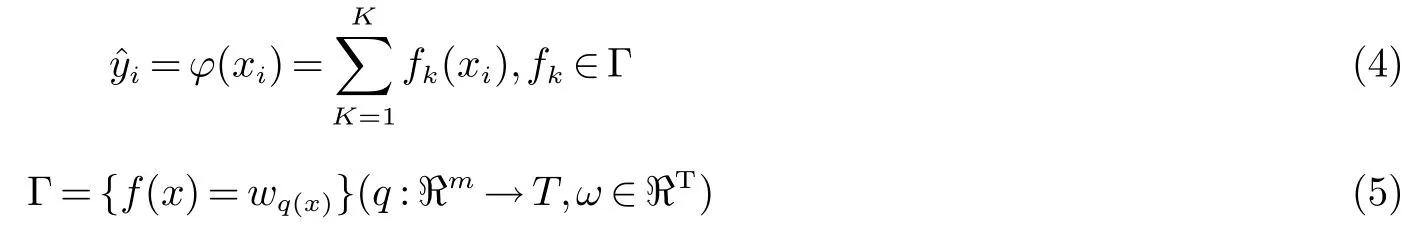
其中，q表示将记录映射到相应的叶索引的每个树的结构，T是树上的叶子数；每个f对应一个独立的树结构q和叶子权重w；用Wi表示第i个叶上的分数.利用线性搜索估计叶节点区域的值，使损失函数极小化，然后更新回归树.

2 道路安全影响因素和指标选取

2.1 道路安全影响因素数据

交通事故成因复杂、随机性强，受人、车、路、环境（自然环境和社会环境）四方面因素影响[17].本文收集到的数据包括：国民生产总值（GDP）(亿元)、人均GDP(元)、公路里程(万kM)、高速等级路公路里程(万kM)、民用汽车拥有量(万辆)、汽车驾驶员人数(万人)、旅客运输量(万人)、公路客运量(万人)、年末总人口(万人)、男性人口(万人)、女性人口(万人)、城镇人口(万人)、乡村人口(万人)、交通事故死亡人数总计(人)等信息.所使用数据均来源于中国国家统计局，表1为1997-2016年道路交通安全相关数据样例.

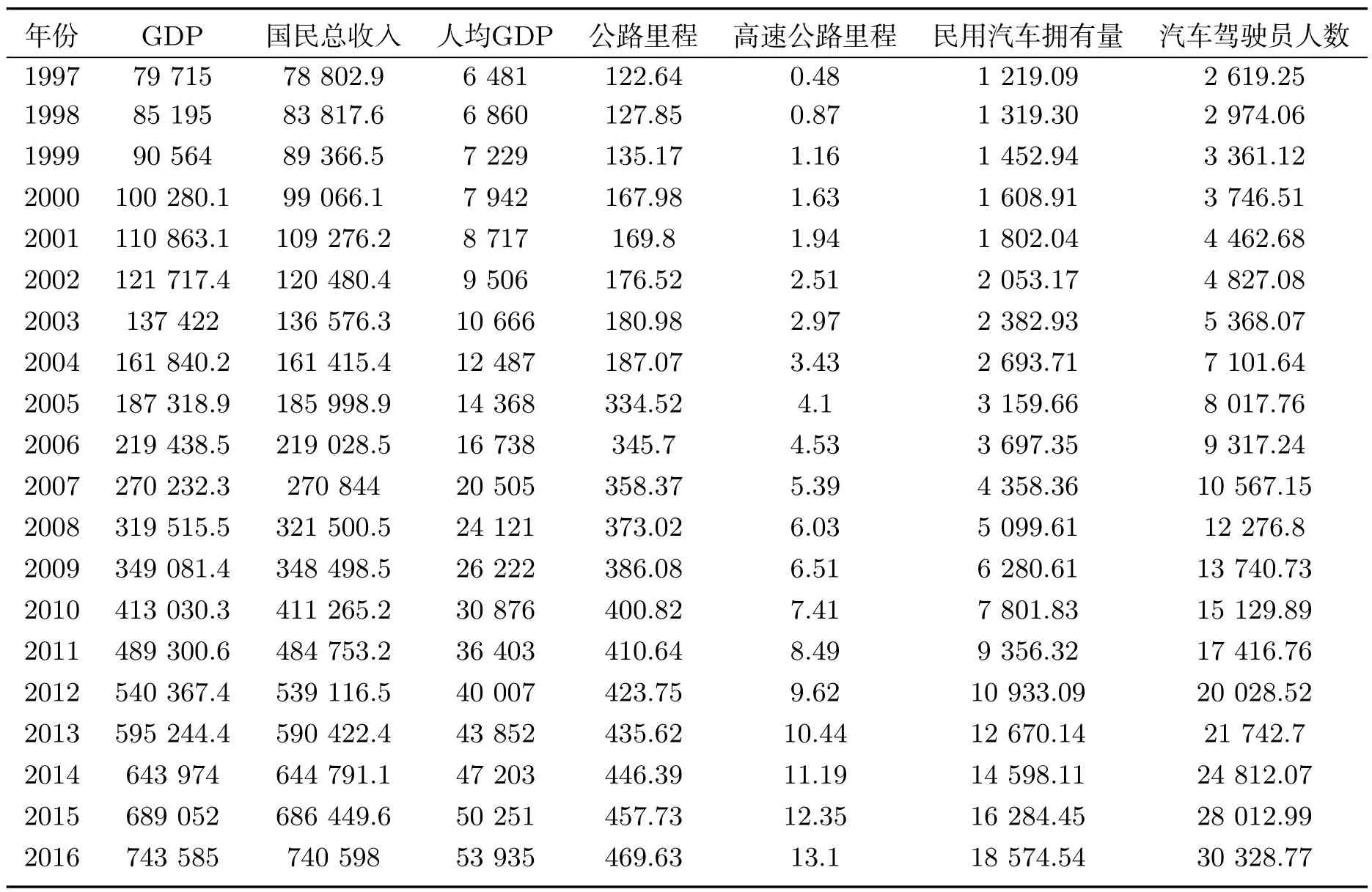
表1 1997-2016年道路交通安全原始数据样例Tab 1 Samples of original road traffic safety data for 1997-2016

续表1 1997-2016年道路交通安全原始数据样例Continued Table 1 Samples of original road traffic safety data for 1997-2016

2.2 性能评价指标

一般的回归预测模型使用均方根对数误差（RMSLE）和决定系数（R-square）来衡量模型的拟合能力.均方根对数误差和决定系数公式如下：

其中n为样本数，y0为原始值，yp为预测值，Ymean为样本均值.

2.3 变量关联分析

为了消除数据选择时的人为干扰因素，进行变量关联分析工作必不可少，否则预测结果可能会受影响[18].本文通过比较每组变量的卡方值和皮尔森相关系数来确定变量间的关联度.卡方值计算公式如下：

上式子中r代表相关变量编号，c 代表目标变量编号，d=(r−1)∗(c−1)一般表示自由度，表示第k组变量，fij表示变量Vk的频率.

下式为皮尔森相关系数：

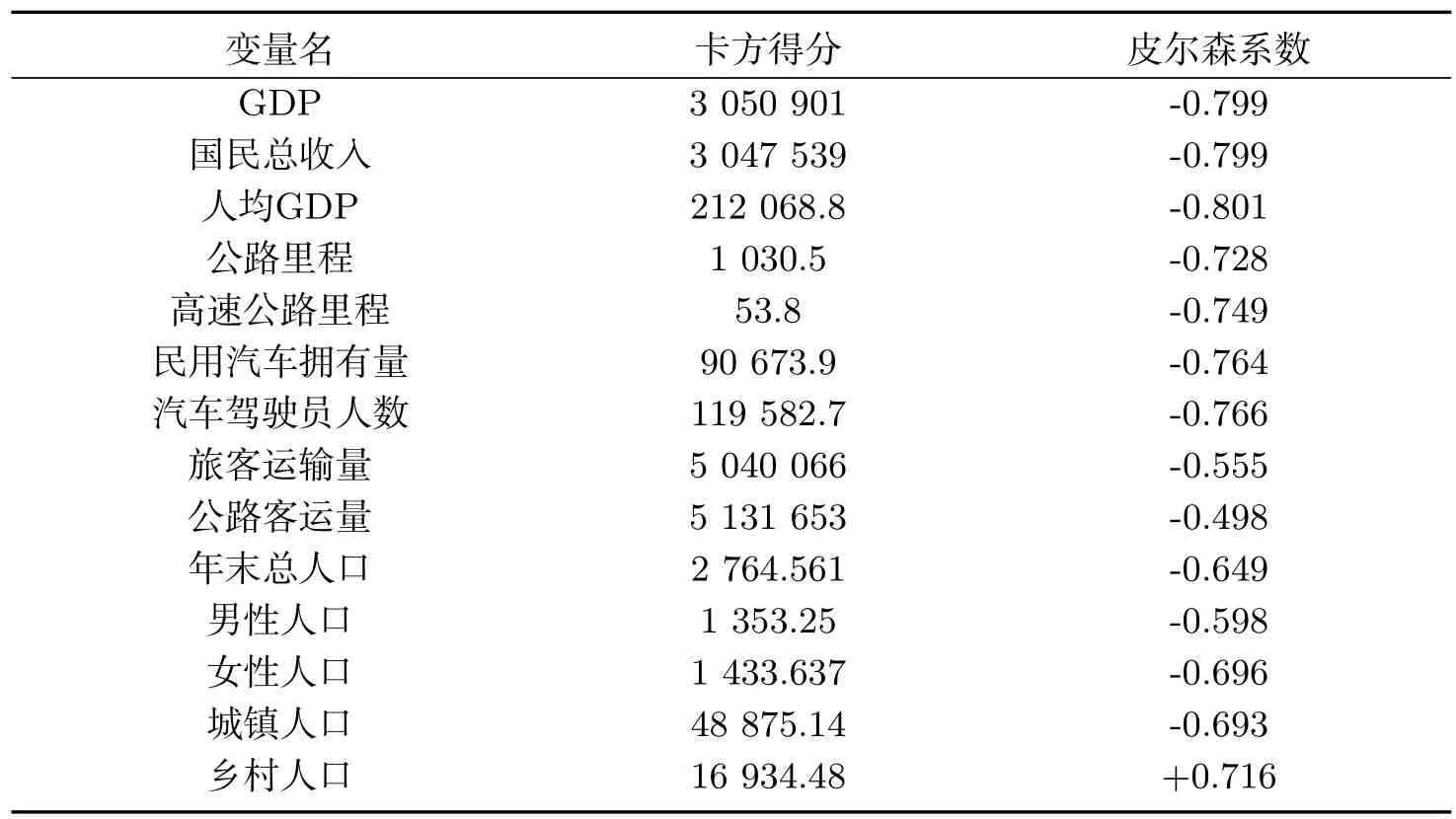
表2 卡方值与皮尔森系数值Tab 2 Chi-square value and Pearson coefficient value

根据表2结果进行特征变量的分析，卡方检验得分小表示变量关联性弱，所示剔除了高速公路里程这一特征；皮尔森相关系数的绝对值越小，则相关程度越小，所以剔除了公路客运量这一特征.最终保留了12类道路交通事故相关特征.

3 道路交通安全预测的GBRT模型

3.1 正则化

这里的I是一个可微凸损失函数，用来度量预测I和目标yi之间的差异.第二项2惩罚了模型的复杂性.平滑处理学习权重，可以避免过拟合.

3.2 超参选择

模型的超参主要包括：学习率、估计器个数、树的最大深度、叶子节点所需的最小样本.损失函数使用最小二乘法，在模型超参变量不多，控制单一变量后，根据实验测试结果来确定其他的超参.GBRT中超参个数较多，可利用GridResearchCV自动寻找最优超参.设定学习率分别为0.1、0.05、0.01.考虑到本例中数据样本少，样本内部分裂节点和叶子节点所需的最小样本都设置为1∼5之间，估计器的个数首先使用Skit-learn的默认值100.通过使用上述的参数，实验返回得一组最佳超参：学习率为0.1，样本内部分裂节点为2，叶子节点所需的最小样本为1.确定以上3个超参后，设定估计器个数为1∼500.根据训练误差和测试误差的变化图来确定最佳的估计器个数.图2为训练集测试集样本误差图.

训练误差80附近趋于稳定，不再有明显的降低，此时的测试集误差也基本趋于稳定，在一定的范围内上下波动.故最终确定估计器的个数为80.表3为模型最终超参数据表.

图2 训练集测试集样本误差图Fig 2 Diagram of sample error of training set test set

表3 模型的超参数据表Tab 3 Super-parameter data sheet of the model

4 实验对比分析

4.1 实验环境

本例实验使用了个人笔记本电脑开发语言为python，调用了Keras所提供的LSTM等神经网络模型，调用了skit-learn提供的GBRT模型.

4.2 实验设计及结果分析

实验模型包括多元非线性回归（MUL）、BP神经网络模型（BP）、长短期记忆神经网络模型（LSTM）、梯度增强回归树模型（GBRT）.数据样本构建模式根据第t-1年12组事故相关特征和t-1年道路交通事故死亡人数来预测第t年的道路交通事故死亡人数.由于最后一年数据预测结果未知，因此数据集共19条，本文以前15条为训练集，后4条数据为测试集.图3为交通事故死亡人数的真实趋势图.

图3 1998-2016年交通事故死亡人数趋势图Fig 3 Trends in deaths from traffic accidents in 1998-2016

图4 四类模型拟合效果图Fig 4 Four-class model fitting effect diagram

通过对上述4种模型分别进行的建模、训练、参数调优工作，各模型在测试集中的预测结果如表4所示.

表4 测试集预测结果Tab 4 Test set prediction results

由表4看出，BP神经网络模型和MUL回归模型预测结果偏差较大.LSTM神经网络模型在2013∼2015年预测结果很接近真实值，但在2016年预测结果偏差突然增大.GBRT模型的预测结果没有波动特别大的样本，总体预测效果保持稳定.

分析图3中的实际死亡人数的趋势图后发现，2016年为时间段内拐点年份，而前3年的趋势与训练数据集中趋势保持一致，2016年的趋势发生改变.实验结果说明LSTM模型确实学习到了数据中的时间依赖信息，但模型的鲁棒性不高，对拐点处预测误差大.而GBRT模型的基模型为回归树，所以预测结果鲁棒性高.

图4为四类模型的预测结果与真实值的拟合图.

为了更好的对模型性能进行量化分析，我们使用了均方根对数误差、决定系数、模型训练耗时三项指标来分析模型性能，表5为各项指标结果.

表5 四类模型的各项指标结果Tab 5 Results of the indicators of the four types of models

均方根对数误差结果显示，GBRT模型的预测误差最小，数值达到了0.018 9.决定系数结果显示，GBRT模型的决定系数值最接近1，达到了0.996 1.训练时间结果显示，GBRT模型的训练时间最短，耗时0.129 6 s.由于神经网络模型需构造复杂的网络进行迭代至收敛，所以耗时明显高于其他类别模型.本例中LSTM神经网络和BP神经网络的训练时间比MUL回归模型和GBRT模型高数十倍.上述三类指标GBRT模型都表现出了最佳的实验结果.

5 鲁棒性分析

基于GBRT模型的交通事故预测模型鲁棒性可以从数据集和模型特性两方面进行分析.一方面数据集时间周期为较为宏观的年周期，所以鲁棒性较高；另一方面模型使用boosting策略，通过基于泛化性能相当弱的学习器构建出很强的集成模型，可以大大降低偏差；同时，为防止过拟合，我们选择了简单的估计器和深度很浅的回归树，来降低方差、提高模型的鲁棒性.

6 结束语

集成学习类模型在各类竞赛中应用活跃，且常常表现出优异的性能，值得在更多的领域进行应用探索.本文提出的基于GBRT模型的道路交通事故预测模型就属于集成学习类模型.通过与传统的回归模型、传统的BP神经网络模型及LSTM神经网络模型对比，结果显示：GBRT模型对同数据的拟合能力最强，变量对预测值的可解释性也最佳，且比神经网络模型的训练时间更短.针对现有模型时间拐点数据预测精度差的问题，GBRT具有更高的鲁棒性来进行预测.更准确的预测结果能帮助交通管理部门提出更可靠决策方案.

后续研究中，以下几方面有待提升：（1）收集更丰富的数据.包括更多道路交通事故相关特征，更多的数据样例，更加精细的时间周期.丰富的数据能够大幅提升模型的性能.更加精细的时间周期能够更好给相关部门提供辅助决策.（2）优化改进模型.本例中只是将GBRT模型在新的领域内进行了应用，未来可以进一步改进优化模型，应用到更广阔的领域.