线性代数中向量内积及正交化几何意义的教学研究

郭冰阳 周双双

（湖南城市学院理学院 湖南益阳 413000）

线性代数主要研究有限维线性空间及线性变换代数结构的学科，它广泛应用于科学技术的各领域。运用线性代数在高维线性空间里研究问题，先要构造一组标准正交基。在向量的内积和正交化这一节中，线性代数教材都是从出发，将直角坐标系的一个常用的基， ，推广到中，通过一系列的定义和定理讲述怎样得到一组标准正交基。至于为什么要构造标准正交基，标准正交基有什么优势，教材中都没有涉及。因此，尽管教材中定义定理表述得很清楚，但学生对定义定理的本质不理解，仅仅觉得是概念和定理的堆砌，不明白其作用。为了帮助学生将抽象的代数内容转换为空间几何的形象理解，在讲授中，我们结合向量间的空间关系，通过空间几何关系的演示，讨论向量内积和正交化的几何意义，使结论具体呈现，从而学生能够理解问题本质，做到学以致用。

一、向量内积的几何意义

向量的内积也叫数量积，以三维为例，有两种定义：[1]

二、标准正交基的几何意义

线性代数教材指出，如果基向量互相垂直，就是正交基，而且每个基向量的长度等于单位长度1，这个基就叫标准正交基。为什么要得到标准正交基呢？学生对从天而降的一大堆定义疑惑不解。讲授这一内容时，我们从内积的几何意义开始引入。

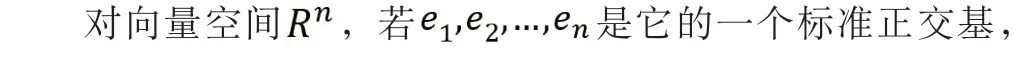
三、施密特正交化的几何意义

线性代数中向量的内积及正交性是连接几何问题和代数问题的桥梁，可以将几何代数化，代数几何化。这也是在高维空间研究问题的基础，更加是线性代数后续内容——实对称矩阵对角化的理论基础。在对这内容的教学中，我们引导学生结合几何背景来理解定义和定理，达到事半功倍的效果。