重型卡车空气滤清器前进气系统性能仿真与结构改进

时丕东， 王仁人b， 曹 芳， 孙志平

(齐鲁工业大学(山东省科学院)a. 机械与汽车工程学院， b. 电气工程与自动化学院， 山东济南250300)

前进气系统作为空气滤清器和发动机的保护屏障，在滤除空气中的大型杂质和雨水方面有极为重要的作用。车辆进气滤清系统一般分为粗滤和精滤，前进气系统又称为空气预滤器,在进气系统中发挥粗滤的作用。目前空气预滤器的结构大致可分为离心式预滤器、油浴式预滤器、静电-旋风管式预滤器，另外还有一些新式预滤器[1]，国外有唐纳森、弗列加、胡默尔、马勒等知名空气滤清器供应商。国内对于空气滤清器及其前进气系统的研究较少。尚明[2]研究了重型卡车干湿复合式空气滤清器的结构设计，探讨结合流体力学及空气动力学相关原理，数值模拟了空气滤清器内部流场，为结构优化设计以及提高过滤效率等提供了理论依据。王仁人等[3]对重型卡车前进气系统旋流式分离器进行了改进设计，得出不同排气口半径时的内部流场，分析得到了流动阻力最小值时的排气口尺寸。刘芹[4]研究了柴油机干湿复合式空气滤清器的性能，通过研究流动情况得出了一种求解其内部压力损失的方法。程家磊等[5]通过研究栅格的角度和挡雨片对空气滤清器前进气道的影响，得出了降低压力损失的结构。王洪亮[6]研究了重型卡车用空气滤清器前进气管的内部流场，通过改变几何半径获得优化方案。

综合目前的研究现状和进展， 发现对于空气滤清器及其前进气系统仍存在研究的不足。 作为重型卡车发动机空气管理系统系列研究的一部分， 本文中对重型卡车空气滤清器前进气系统进行整体流场研究、 分析， 并进行结构改进， 以解决分块研究对接边界条件不一致、 不连续导致模拟结果局限性的问题。 采用Fluent软件， 运用离散相模型(DPM)两相耦合的方法对重型卡车空气滤清器前进气系统进行仿真， 以实现结构优化。

1 计算方法与模型建立

1.1 几何模型

本文中模拟所采用的模型为某重型卡车空气滤清器前进气系统，内部结构如图1所示。由于内部结构较复杂，不易直接进行模拟，因此，利用Geomertry前处理软件提取前进气系统内部流体域，并进行简化处理，得到模拟的内部流体域模型，如图2所示。

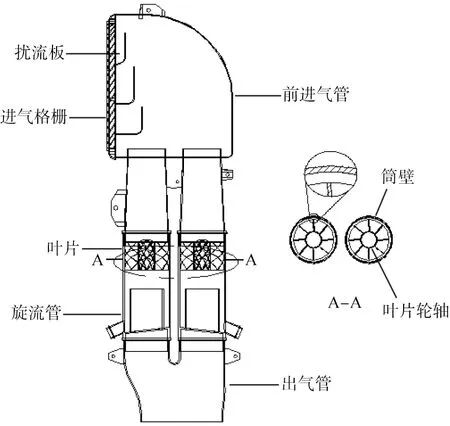
A-A—叶片部位的剖切位置。图1 重型卡车空气滤清器前进气系统内部结构示意图

图2 模拟的重型卡车空气滤清器前进气系统内部流体域模型

1.2 网格划分

本文中的网格模型采用ANSYS Fluent Meshing软件生成的多面体网格，多面体网格生成快捷，对复杂的结构外形有很高的适应性[7]， 能像四面体一样便捷生成，在计算效率方面也比非结构网格更高效。由于每个多面体单元可以有很多个相邻的单元，因此对于变形较大的区域，可以更准确地预测流动情况。对生成的网格进行质量检查，没有负体积，最小正交质量均大于0.3，光顺性较好，网格质量较高，划分的重型卡车空气滤清器前进气系统内部流体域网格如图3所示。为了精确仿真壁面附近流动情况，将壁面附近网格划分为5层，得到该空气滤清器前进气系统内部流体域的边界层网格如图4所示。

图3 重型卡车空气滤清器前进气系统内部流体域网格

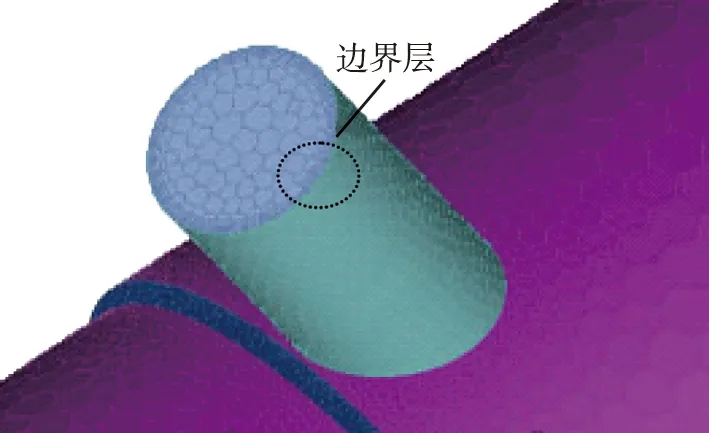
图4 重型卡车空气滤清器前进气系统内部流体域的边界层网格

1.3 边界条件设置

边界条件对流体计算结果的准确性和稳定性有很大的影响。本文中研究的连续相为空气，空气体积流量为1 800 m3/h，连续相求解的边界条件设置如表1所示。

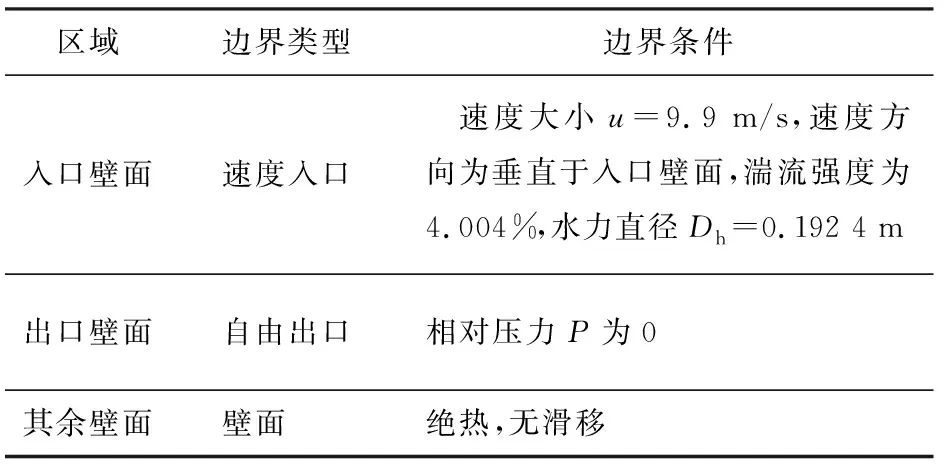
表1 连续相求解的边界条件设置

对于离散相，采用DPM两相耦合方法进行模拟。DPM模型适用于颗粒体积分数小于10%的情况，采用拉格朗日方法求解颗粒的运动轨迹方程。在连续相收敛后加入DPM，再进行耦合计算，可以精确求解颗粒的运动情况及此时的流场状态。将颗粒假设为10组粒径不同的球形颗粒，相间无作用力，分布均匀，密度为2 650 kg/m3，粒径的分布符合《道路车辆—用于滤清器评定的试验粉尘 第1部分：氧化硅试验粉尘》[8]的要求，颗粒模型粒径分布具体情况如图5所示。

图5 颗粒模型粒径分布

1.4 数学模型

将前进气系统内部复杂流场抽象为数学模型进行数值模拟，连续相采用欧拉方法进行仿真求解，流动过程假设为三维不可压缩稳态流动，颗粒相看作离散相运用拉格朗日方法进行模拟仿真，求解颗粒运动轨迹及受力的情况。

1.4.1 湍流模型

通过计算求解出模拟流体的雷诺数为0.960 5×105>10 800,因此，流体的流动状态为湍流流动[9]，湍流强度为4.004%，为充分发展流动。

采用重正化群(RNG)k-ε双方程湍流模型(其中ε为湍动能的耗散率，k为湍动能)进行求解计算，标准k-ε模型有合理的计算精度和较好的稳定性，可以更好地模拟高雷诺数的湍流计算模型,而RNGk-ε模型是标准k-ε模型的改进方案，可以更准确地模拟强旋流或者带有弯曲壁面的流动[10]。

1.4.2 连续相控制方程

仿真中气体的运动情况遵循连续相控制方程，通过计算流体动力学(CFD)方法求解计算，得出流场流动信息。

质量守恒方程为

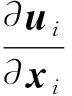
(1)

式中：ui为速度矢量；xi为位移矢量；i取值1、 2、 3。

动量守恒方程为

(2)

(3)

其中

μeff=μ1+μt，

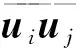
k方程为

(4)

式中：αk为k方程的Prandtl数；Gk为湍动能k的产生项。

ε方程为

(5)

其中

(6)

(7)

(8)

式中：αε为ε方程的Prandtl数；Eij为时均应变率；C1ε、C2ε、η0、β为模型常数。式(4)、(5)、(6)中模型常数的取值如表2所示。

表2 模型常数的取值

1.4.3 离散相控制方程

利用Fluent软件，通过离散相控制方程，在拉格朗日坐标中对离散相进行求解，得出颗粒的运动轨迹。 运动控制方程为

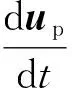
(9)

轨迹方程为

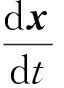
(10)

(11)

(12)

(13)

式中：Mp为颗粒质量；t为时间；u为连续相的运动速度；up为颗粒的运动速度； dx为颗粒的运动位移； ∑F为颗粒受到的所有力在运动方向上分力的代数和；Fd(u-up)为颗粒单位质量曳力；g为重力加速度；Fx为沿x轴方向的作用力；μ为空气动力黏度；Cd为曳力系数；ρp为颗粒密度；dp为颗粒粒径；Re为颗粒和连续相的速度差的雷诺数。

2 网格无关性检验

研究[11]表明，在网格数量相近的情况下，多面体网格的计算精度可以比四面体网格更精确，但是在某种程度上，网格的数量会对模拟结果的精度和计算效率产生较大的影响，只有保证一定的网格数目，才会得到更精确的计算结果[12]。为了验证研究的准确性，将模型网格划分为279 374、 843 325、 1 207 794、 1497 349、 2 546 163共5个数量等级，分别进行模拟研究，以相对出口静压为评价指标，得到出口相对静压随网格数量的变化关系，如图6所示。由图可知，当网格个数大于1.2×106时，计算结果趋于一致， 并且计算结果相对误差小于5%，本文中所有模拟计算网格个数均大于2.0×106，可以达到模拟流场精度要求。

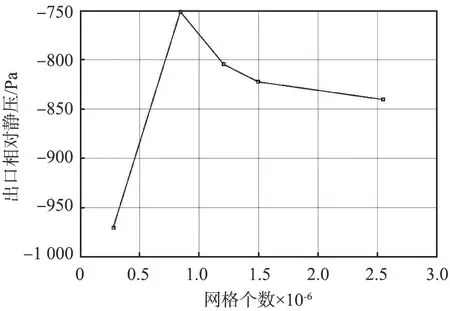
图6 出口相对静压随网格数量的变化

3 仿真结果与分析

前进气系统的主要性能包括原始压降、过滤效率和储灰能力等，压降会影响发动机的充气效率，进而影响发动机的功率，过滤效率影响空气滤清器和发动机的使用寿命。压降可以通过计算进出口的平均压力，作差求得。过滤效率为

(14)

式中：nc为被捕捉颗粒数；nf为入射颗粒数。

3.1 整体压力场和速度场分析

图7所示为重型卡车空气滤清器前进气系统原结构整体流场云图。由图7(a)可知，进气栅格处压力较大，栅格前、后存在较大压力梯度，原因是气流由入口进入栅格时，进气通道变窄，流动阻力较大，部分压力势能转变为相对动能。 叶片及其后方压力为负值， 原因是气流经过叶片的螺旋通道被加速， 压力势能减小， 动能增加，经过流通面积更小的排气管时，压力势能进一步减小，向动能转变。由图7(b)可知， 栅格处和叶片及后方排气管处气流速度较大，气流在叶片处呈现出靠近中心部位速度大，靠近边缘逐渐减小， 该速度梯度可以使灰尘颗粒获得更大的离心力，利于灰尘颗粒的过滤。

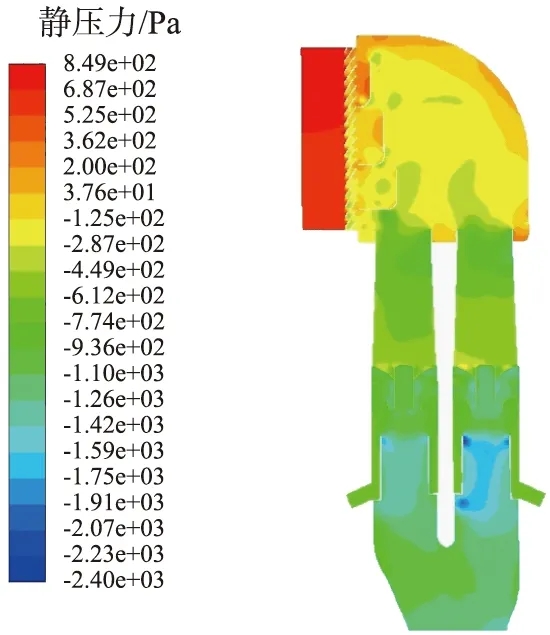
(a)压力云图

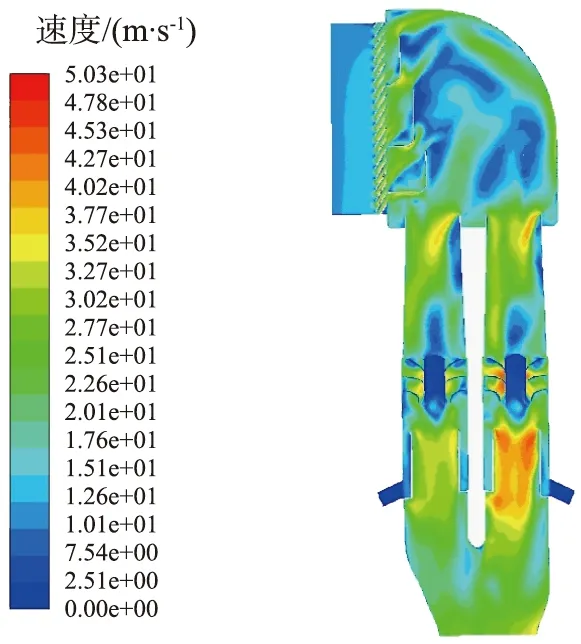
(b)速度云图图7 重型卡车空气滤清器前进气系统原结构整体流场云图

3.2 颗粒运动轨迹

采用DPM模型[13]计算重型卡车空气滤清器前进气系统内颗粒运动轨迹， 如图8所示。 由图可以看出， 大部分粒径为1～5 μm的颗粒直接进入排气管逃逸， 对于粒径大于20 μm的颗粒， 过滤效率均大于92%， 说明目前结构对于小颗粒的过滤效率较低，原结构与经试验验证的粒级效率分布，如图9所示， 其中图9(a)所示为原结构的粒级效率，图9(b)

图8 重型卡车空气滤清器前进气系统内颗粒运动轨迹

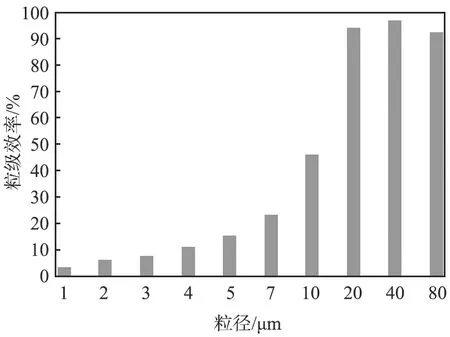
(a)原结构的粒级效率

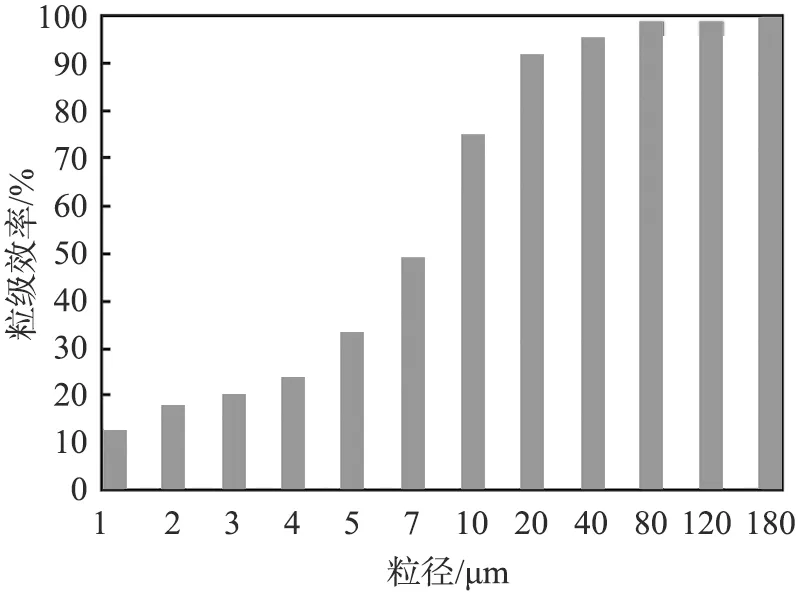
(b)经试验验证的粒级效率[14]图9 重型卡车空气滤清器前进气系统原结构与经试验验证的粒级效率分布

所示为唐莲花等[14]经过试验验证的粒级效率。通过对比发现，本仿真结果与文献[14]中流量为1 900 m3/h的粒级效率结果趋势基本一致。

3.3 仿真数据分析

通过对仿真数据统计分析得知，重型卡车空气滤清器前进气系统原结构过滤效率为39.88%，原始压降为1 838 Pa。整体结构的压力损失较大，对于细小颗粒的过滤不足，大粒径颗粒的过滤效率有待进一步提高，过滤效率偏低，叶片部位速度对于过滤效率和阻力影响较大，需要进行结构优化。

4 结构改进

根据对整体结构的仿真分析，为了降低重型卡车空气滤清器前进气系统的整体压降，改善其过滤性能，研究通过对不同叶片几何参数及筒壁参数尺寸进行仿真分析，以得到最优的结构，以压降不大于1 838 Pa以及过滤效率不小于39.88%为目标进行结构改进。

4.1 叶片轮轴改进

图10所示为重型卡车空气滤清器前进气系统压降与过滤效率随轮轴直径变化的关系。由图可以看出，压降随叶片轮轴直径的增加而增加，轮轴直径为27.78 mm时压降最小；由过滤效率情况可知，在叶轮轮轴直径为57.78 mm时，过滤效率最高，在直径为27.78 mm时，过滤效率最低。

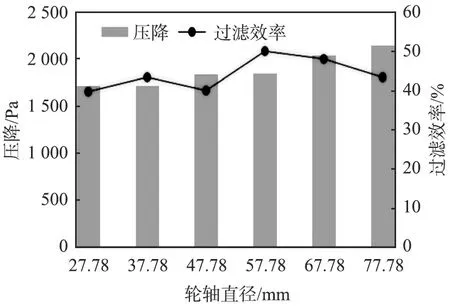
图10 重型卡车空气滤清器前进气系统压降与过滤效率随轮轴直径的变化

综合分析， 当叶片轮轴直径为57.78 mm时， 前进气系统的过滤效率比原结构轮轴直径为47.78 mm时的提高10.07%， 压降比原结构增加11 Pa， 压降增加幅度较小。

4.2 叶片边缘与筒壁间隙改进

当轮轴直径为57.78 mm时，过滤效率较高，但是压降增大，在此基础之上进行进一步优化。以叶轮轮轴直径为57.78 mm的前进气系统为优化基础，考虑叶片边缘与筒壁的间隙(以下简称间隙)对前进气系统的影响。

表3所示为压降与间隙的关系。由表可知，间隙为22.25 mm时压降最小，原因为间隙增大，流通面积增加，局部阻力减小，使总体压降减小；间隙为7.25 mm时压降最大，此时叶片部位涡流较多，因此流动阻力最大。

表3 重型卡车空气滤清器前进气系统压降与间隙的关系

图11所示为重型卡车空气滤清器前进气系统压降随间隙变化的拟合曲线。由图可以看出，随着间隙的增大，压降呈现先增大后减小的趋势，在原结构间隙4.25 mm左侧至0 mm处压降逐渐减小，在其右侧至7.25 mm处逐渐增加。

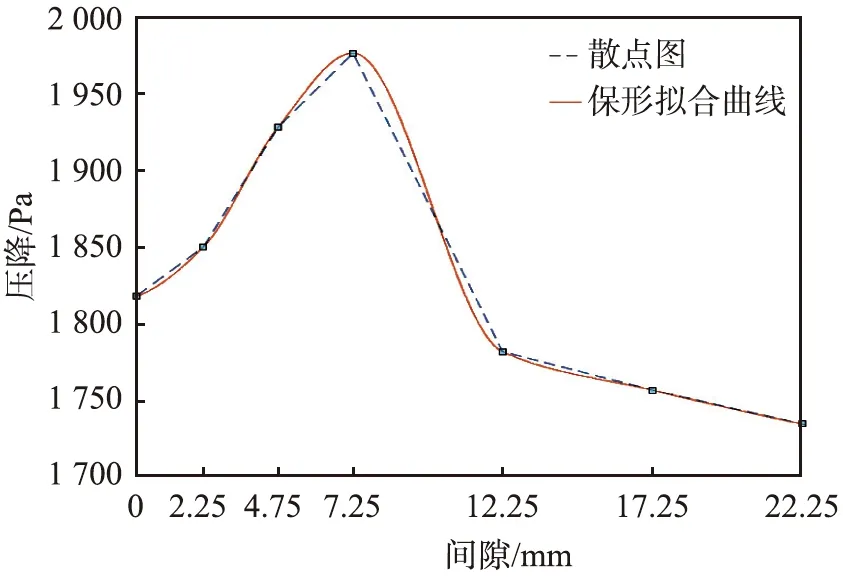
图11 重型卡车空气滤清器前进气系统压降随间隙变化的拟合曲线

重型卡车空气滤清器前进气系统的分离性能分为过滤效率和粒级效率，粒级效率反映前进气系统对小颗粒的过滤性能。表4所示为过滤效率与间隙的关系。由表可知，随着间隙的增大，叶片直径减小，使得颗粒受到的离心力减小，从而使颗粒的逃逸量增加，过滤效率降低。

表4 重型卡车空气滤清器前进气系统过滤效率与间隙的关系

过滤效率与间隙的函数关系为y=-0.000 9x3+0.11x2-3.3x+55，0≤x≤22.25，其中, 自变量x为间隙的大小，因变量y为过滤效率。经计算，最大值为x=0 mm，y=55%。

图12所示为空气滤清器前进气系统不同间隙时的粒级效率的曲线。由图可知，粒级效率随间隙的减小而呈现出增大的趋势，当间隙减小至0 mm时，粒径为1～5 μm的微小颗粒和粒径大于20 μm的大颗粒的过滤效率均处于最大值水平。

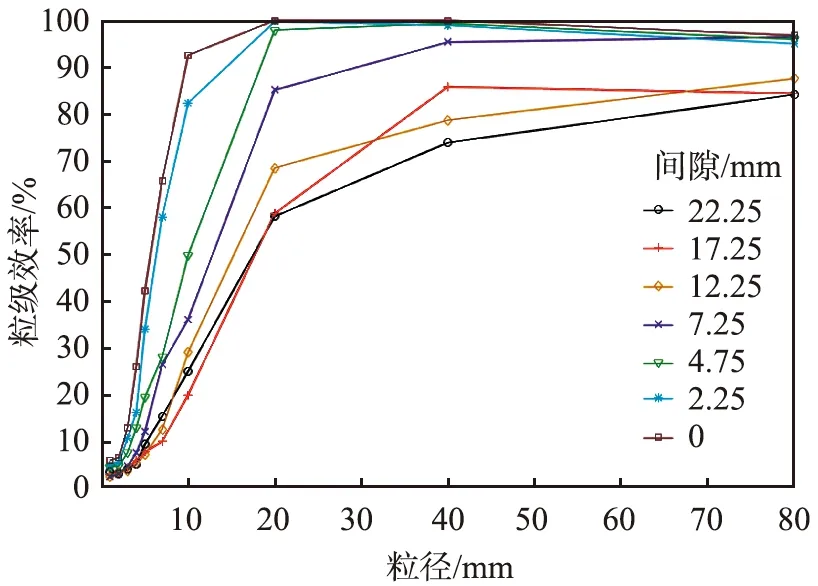
图12 重型卡车空气滤清器前进气系统不同间隙时的粒级效率

为了进一步研究叶片轮轴与间隙耦合情况下对前进气系统的压降和过滤效率的影响，采用逐步收敛法[15]对参数进行优化，即先固定一个优化参数去优化另一个参数，然后再优化第1个参数，最终循环至优化的结果不再变化。

以上分析完成了第1步优化， 下一步在间隙为0 mm时，再次对叶片轮轴直径进行优化。通过模拟分析，得到间隙为0 mm时压降、过滤效率与轮轴直径的关系，如图13所示。由图可以看出，在间隙为0 mm时，压降和过滤效率均随轮轴直径的增加而增大，当轮轴直径增大至67.78 mm时，压降超过1 900 Pa，轮轴直径为77.78 mm时过滤效率最大，压降大于2 000 Pa。 在压降不超过原结构压降的前提下，轮轴直径为57.78 mm时过滤效率最大， 因此， 可取轮轴直径57.78 mm作为优化参数。

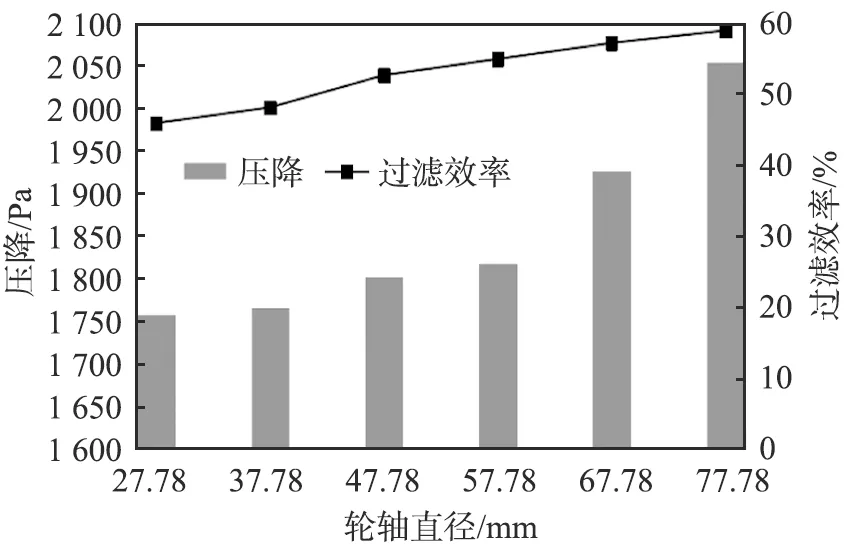
图13 重型卡车空气滤清器前进气系统间隙为0 mm时压降、过滤效率与轮轴直径的关系

综合分析叶片轮轴和间隙及其耦合情况对前进气系统的影响，确定叶片轮轴直径为57.78 mm、叶片与筒壁间隙为0 mm作为改进方案。

4.3 叶片直径与筒壁内径联合分析

为了进一步研究前进气系统的性能，对叶片与筒壁内径进行联合仿真分析，联合分析在叶片与筒壁间隙为0 mm的优化基础之上进行，即叶片直径与筒壁内径同时变化，得到压降与过滤效率随叶片直径和筒壁内径的变化规律，如图14所示。由图可知，压降随叶片直径与筒壁内径的增大而呈现出先大幅减小后逐渐增大，当叶片直径与筒壁内径为153.4 mm时取最小值；过滤效率随叶片与筒壁参数的增大而呈现出先大幅增大后逐渐减小，最大值出现在153.4 mm处。通过压降与过滤效率的变化趋势可以看出，叶片直径与筒壁的内径减小时对前进气系统性能的影响大于增大的情况，叶片与筒壁参数大于153.4 mm时，压降与过滤效率均优于小于153.4 mm时的结构参数。

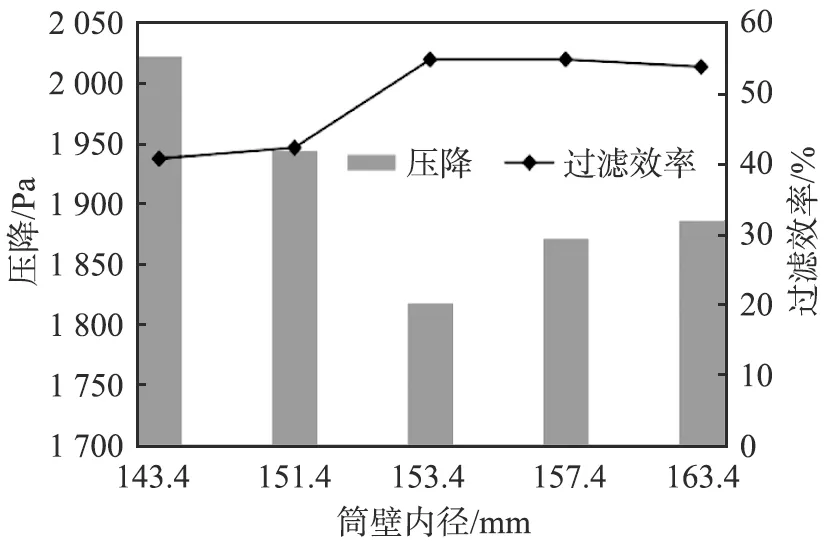
图14 重型卡车空气滤清器前进气系统压降与过滤效率随叶片直径和筒壁内径的变化

根据以上分析结果，最终确定重型卡车空气滤清器前进气系统的改进方案如下：以叶轮轮轴直径为57.78 mm，叶片边缘距筒壁的间隙为0 mm(即叶片直径增大至153.4 mm)作为最优改进方案。 叶片参数优化前、 后的参数对比如表5所示。 由表可知， 优化后的过滤效率相比原结构的提高14.9%， 进气阻力减小20 Pa。 图15(a)所示为优化前、后速度场对比。 由图15(a)可知， 改进后结构， 叶片部位速度均匀性增加，平均速度增大。图15(b)所示为优化前、后压力场对比。由图15(b)可知，叶片两端附近压力梯度变化均匀，说明涡流作用较小，流动阻力减小，达到优化改进的目标。

表5 重型卡车空气滤清器前进气系统优化前、 后参数对比

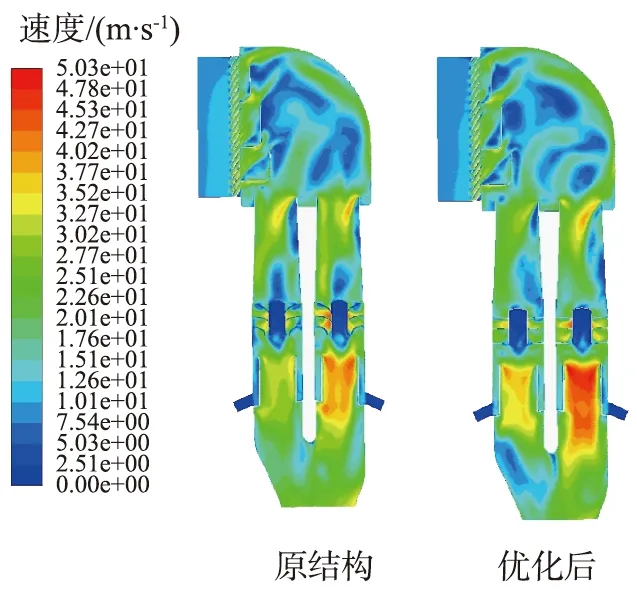
(a)速度云图

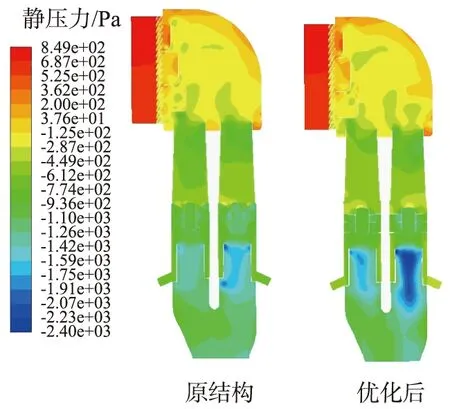
(b)压力云图图15 重型卡车空气滤清器前进气系统优化前、 后速度场与压力场对比

5 结论

本文中为了研究重型卡车空气滤清器前进气系统整体性能，基于CFD方法进行数值模拟仿真，并与经试验检验的计算数据进行对比，验证了DPM仿真模型的可行性，分析了叶片轮轴直径、叶片边缘与筒壁的间隙及叶片直径与筒壁内径参数对前进气系统压力损失和过滤效率的影响，得出以下结论：

1)通过网格无关性检验研究了网格数量对模拟结果精度的影响，当网格个数大于1.2×106时，计算结果趋于一致，验证了网格模型的可行性。

2)重型卡车空气滤清器前进气系统的压降随叶片轮轴直径的增加而增大， 随叶片边缘与筒壁的间隙的增大呈先增大后减小的趋势，随叶片直径与筒壁内径的增大呈先大幅减小后逐渐增大的趋势。

3)过滤效率随叶片边缘与筒壁间隙的增大而减小，当叶片轮轴直径为57.78 mm、叶片边缘与筒壁的间隙为0 mm时，过滤效率提高14.9%，同时对于微小颗粒的过滤效率显著提高，说明叶片几何结构参数对于前进气系统的过滤效率影响较大。

4)与原前进气系统相比，改进后的结构叶片部位的速度和压力均匀性提高，平均速度增大，流动阻力下降，整体工作性能改善。