初探初中几何辅助线的添加策略
2020-03-04樊勃
樊 勃
(黑龙江省齐齐哈尔市第二十八中学 黑龙江齐齐哈尔 161000)
几何是初中数学学习的基础模块,它可以让学生在图形的探究过程中感受到数学的魅力,产生学习兴趣,实现数学推理、想象与判断能力的提升。在解决几何问题时合理的添加辅助线可以让复杂的图形变得更加容易观察、对比,以此快速找到解题方法。但是,对于初中生来说辅助线的添加方法并不容易掌握,需要学生长期的练习与思考。下面,笔者对初中几何辅助线的添加方法进行了探讨,仅供参考。
一、中点法
如果在几何题目中给出了“中点”“中线”等条件,那么我们在解决问题时可以将思考的重点放在线段的中点处,通过中位线定理确定各线段之间的关系,或是求证三角形之间的全等关系,以此从题目中找到更多的已知条件,获得解题思路。
例1:如图,点E、点F是线段BC、AD的中点,且AB=CD,射线BA与射线EF相交于点G,射线CD与射线EF相交于点H,求证∠BGE=∠CHE。
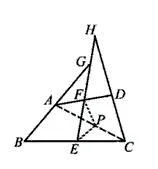
分析:因为点E、点F 是线段B C、AD的中点,所以我们可以尝试将AC连接在一起,并取其中点P,构造三角形PEF。只要证明PE=PF,便可以利用三角形中位线的性质证明∠BGE=∠CHE。
证明:连接AC,并在AC上取中点P,连接PE、PF。因为E为BC的中点,所以PE//AB,且2PE=AB,F是BC的中点,则PF//CD,2PF=CD。
已 知 线 段A B = C D , P E = P F , 等 边 对 等 角 可 得∠PEF=∠PFE,因为PE//AB,所以∠BGE=∠PEF,因为PF//CD,所以有∠CHE=∠PFE,所以∠BGE=∠CHE。
二、平行线法
平行线法,是指通过添加某一直线的平行线解决几何问题的方法[1]。这种方法可以证明图形中某些边、角的相等关系。

例2:如图所示,在直角三角形ABC中,点D为斜边AB上的中点,且DEDF,线段DE、DF分别交AC、BC于E、F,求证AE2+BF2=EF2。
分析:求证AE2+BF2=EF2也就是证明三条线段满足直角三角形的三边关系特征,所以我们不妨尝试采用平行线法将AE、BF、EF三条线段整合到同一个三角形之中,通过证明该三角形为直角三角形证明等式成立。
证明:过点A作线段AG//BC,延长线FD与AG交于点G,因为∠ADG=∠BDF,AD=BD,∠GAD=∠B,所以∆DFB与∆DGA全等,所以FB=GA,GD=DF,所以ED为FG的中垂线,EG=EF。连接EG,因为∠GAE=∠C=90°,所以∆AEG为直角三角形,AE2+BF2=GA2+AE2=EG2=EF2,所以AE2+BF2=EF2。
三、连对角线法
在四边形解题过程中,常见的添加辅助线方式就是连连对角线法,特别是在解决特殊四边形问题中,连对角线可以将四边形问题转化为三角形问题,然后再利用三角形性质求解。
例3:如图,ABCD为梯形纸片,AB//CD,AD=BC,翻折纸片ABCD,使点A与点C重合,折痕为EF,CEAB。求EF//BD。
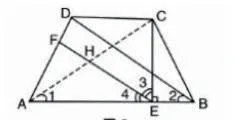
分析:求EF//BD可以从平行线性质入手,通过证明角的相等来证明平行线的相等。在本题中,可以连接AC来建辅助线,然后通过三角形全等分析角与角之间的关系,证明∠AEF=∠ABD,求得EF//BD。
解:连接AC,因为AD=BC,所以ABCD为等腰梯形,根据等腰梯形两底角相等可得∠DAB=∠CBA,所以∆ADB与∆ACB全等。因为EF是折痕,所以EF是AC的垂直平分线,因此,∠1=∠2=45°。又因为CEAB,可得EF平分直角AEC,所以∠3=∠4=45°,∠2=∠4,所以EF//BD。
四、倍长中线法
中线是初中阶段三角形学习中最重要的线段之一,在解决几何问题时常常采用倍长中线的方法来构造辅助线[2]。所谓的倍长中线法就是将图形的中线延长一倍,从而构造出全等三角形,然后再通过全等三角形解决问题,证明答案。
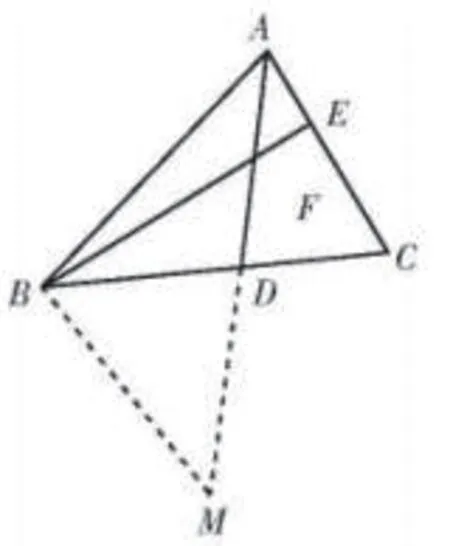
例4:在△ABC中,AD为BC的中线,E为AC上的一点,BE与AD交于F,AE=EF,请判断AC与BF的大小关系。
分析:判断AC与BF的大小关系可以通过三角形的关系来证明,而AC与BF所在并不能直接证明全等,以此便可以考虑通过等量代换的方式进行求解。
解:如图所示,延长A D 到点M,使D M=A D,连接BM。因为AD=DM,所以∠ADC=∠BDM,DC=BD,所以△ADC≌△MDB。所以AC与BM相等,∠DAC=∠M。因为AE=AF,所以∠DAC=∠AFE=∠BFD=∠M,所以BF与BM相等,BF=AC。
五、结束语
除了上述提到的几种方法外,辅助线的添加方法还有很多,例如“高线法”“旋转法”等。添加辅助线没有固定的模式和方法,也没有规律可循,学生只有在日常学习中多思考、多联系,才能够掌握添加辅助线的基本思路,提高几何学习的兴趣。也只有如此,才能让学生在一次次解决问题的过程中提升数学能力,培养数学素养。
