利用简谐运动的对称性巧解阻尼振动问题
2020-03-04
(江苏省南菁高级中学,江苏 江阴 214437)
1 引言
近几年,在江苏省高考物理试题、模拟试题中常常出现弹簧振子在摩擦力作用下运动的物理模型(阻尼振动模型),如2013年第9题、2018年第7题、2019年第8题。弹簧振子在不受摩擦力作用时做简谐运动,对此考生可熟练利用简谐运动的对称性解决相关问题。然而,当振子做阻尼振动时,弹簧振子的运动就不再呈现完美的对称性,整个过程中机械能不断减少,振幅会越来越小,最终停止。这时考生因无法在脑海中形成正确的运动图景而找不到切入点。实际上,当弹簧振子在单方向运动的过程中,弹簧振子即使存在弹簧弹力之外的恒力作用,振子仍然可视为做简谐运动。所以,我们依旧可以利用简谐运动的对称性巧解相关问题,下面对几个典型例题进行分析。
2 典型例题分析
例1:物体从与水平面成α角的斜面上端开始下滑,物体与斜面间的动摩擦因数μ随着物体到斜面上端的距离按μ=bx(b为大于零的常数)的规律变化,物体未到斜面的底部就停下来了,试求物体从开始运动到停下来所经历的时间t。
解析:物体受力如图1所示,设某一时刻物体距离斜面上端的距离为x,根据牛顿第二定律,有:mgsinα-bxmgcosα=ma,当a=0时,有mgsinα=bx0mgcosα,x0即为物体运动的平衡位置,所以:mgsinα-bxmgcosα=bmgcosα(x0-x),规定沿斜面向下为正方向,物体相对于平衡位置的位移Δx=-(x0-x),当x

图1

我们还可利用等效法,即斜面摩擦力相当于一根平行于斜面的弹簧产生的弹力,物体的下滑运动相当于弹簧振子在平行于斜面方向的重力分力作用下的简谐运动。
例2:如图2所示,一轻质弹簧左端固定,右端系一小物块,物块与水平面的最大静摩擦力和滑动摩擦力都为f,弹簧无形变时,物块位于O点。每次把物块拉到O点右侧不同位置由静止释放,释放时弹力F大于f,物块沿水平面滑动一段路程直到停止,下列说法中正确的是( )。

图2
A. 释放时的弹性势能等于全过程中克服摩擦力做的功
B. 每次释放后物块速度达到最大的位置保持不变
C. 物块能够返回到O点右侧的临界条件为F>3f
D. 物块能够返回到O点右侧的临界条件为F>4f
解析:因为有摩擦阻力的存在,物块最终停下来的位置不一定在平衡位置O,所以最终可能依然存在弹性势能,当有弹性势能存在的时候,原来的弹性势能可能只有部分用来克服摩擦力做功,A选项错误;弹簧弹力与摩擦力平衡的位置为物块速度最大的位置,根据f=F=kx,因为摩擦力不变,所以物块速度达到最大的位置保持不变,B选项正确;设物块在最左端受到的弹力是F′,物块向左运动的过程可视为一个简谐运动,物块向右运动的过程同样也可视为另一个简谐运动。根据简谐运动的对称性,在最大位移处回复力大小相等,第一次从最右边运动到最左边的过程中:F-f=F′+f,再恰好向右运动到O点:F′-f=f,联立解得:F=4f,故物块能返回到O点右侧的临界条件为:F>4f,故D选项正确。
通过与例1的类比,可知振子从一端向另一端单方向的运动可视为简谐运动,与一般简谐运动不同的是:由于运动方向的改变,振子的平衡位置不断地发生改变。所以此题我们对两个方向的运动分别运用对称性来解答。
例3:如图3所示,水平桌面上的轻质弹簧一端固定,另一端与小物块相连。弹簧处于自然长度时物块位于O点(图中未标出)。物块的质量为m,AB=a,物块与桌面间的动摩擦因数为μ。现用水平向右的力将物块从O点拉至A点,拉力做的功为W。撤去拉力后物块由静止向左运动,经O点到达B点时速度为零。重力加速度为g,则上述过程中( )。
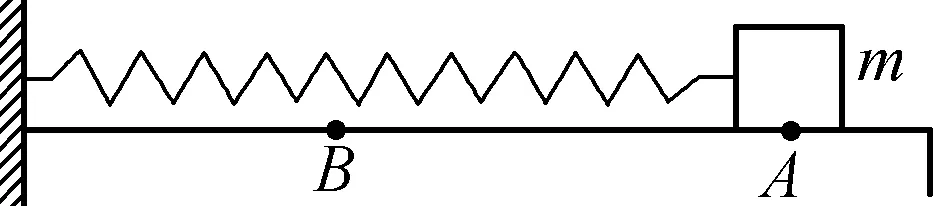
图3

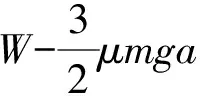
C. 经O点时,物块的动能小于W-μmga
D. 物块动能最大时弹簧的弹性势能小于物块在B点时弹簧的弹性势能

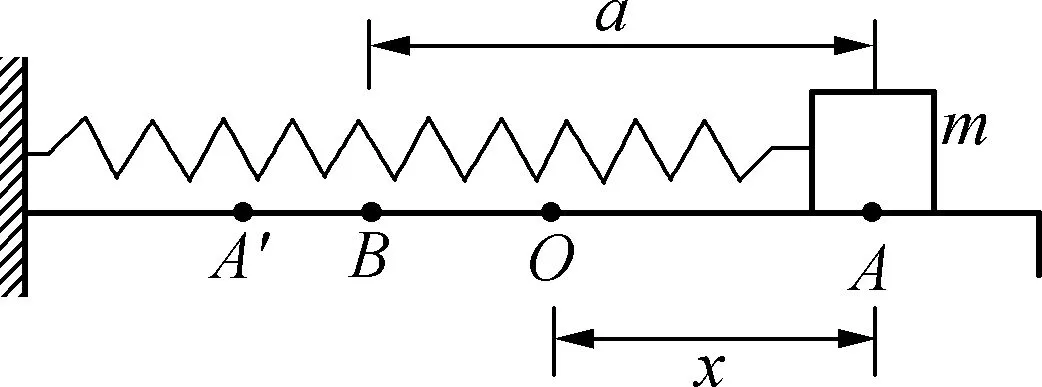
图4

3 结语
当我们在解决阻尼振动问题时可利用简谐运动的对称性,如在例1、例2中阻尼振动单方向上仍然具备简谐运动的对称性,再如在例3中我们可以假设振子不受摩擦阻力的作用,利用我们熟悉的对称性找到振子运动的对称位置,可以相对容易地了解物块运动的过程,从而容易找到解决问题的切入点。
