基于奇异值分解的组合导航可观测度计算

张 丹，裴忠海，余薛浩

（上海航天控制技术研究所，上海201109）

0 引言

高精度导航是航海器能够顺利完成任务的前提保障，航海器既要提高精度，又要确保可靠性。捷联惯性导航系统（Strapdown Inertial Navigation System，SINS）通常作为主导航系统，能够实时输出姿态、速度、位置信息，具有实时性好、短时精度高、输出信息较为全面等优点，但其长时导航误差大。多普勒计程仪（Doppler Velocity Log，DVL）是利用声波在水下传播的Doppler效应进行测速和计程的一种水声导航仪，其具有较高的测速精度[1]。利用Kalman滤波技术可以实现SINS/DVL组合导航，不仅可提高导航系统在无GPS情况下的精度，同时也增强了导航信息的容错性，具有较强的适应性和灵活性[2]。

对于SINS/DVL组合导航的Kalman滤波器[3]，由于初始协方差阵容易满足正定性条件[4]，并且系统状态转移矩阵满足满秩条件，因而系统是完全可控的[5]，则Kalman滤波器的有效性主要取决于系统的可观测性，可观测度是真正反映Kalman滤波收敛精度和速度的重要指标。目前，国内外研究系统可观测度的方法主要有以下几种:1）经典可观测矩阵法。该方法缺点明显，只适用于定常系统，并且计算量巨大；2）Ky3obkob法。该方法仅能初步找出可观测状态的维度与观测状态间的线性关系；3）状态方程解耦法。该方法只能定性分析可观测性，具有主观性[6-8]。因此，本文采用了一种可用于时变系统的分析方法——分段定常系统（Piece-wise Constant System， PWCS）。

对于时变系统，通常采用分段线性定常系统理论[9]计算系统的可观测性矩阵，通过计算可观测性矩阵的特征值或奇异值来定量分析系统状态量对应的可观测度[10-11]。但是，可观测性矩阵的阶数是随时段数量的增加而不断累积的。对于长时间的导航，实时观测变得不太可能[12-13]。因此，需要对可观测矩阵的计算进行改进。本文根据可观测性矩阵的特性，提出了一种改进的简化算法，可以在很大程度上减少系统可观测性矩阵的计算工作量。最后，通过仿真验证及湖面跑船实验，验证了该方法的可行性和合理性，并在此基础上研究了不同航迹机动方式对系统状态量可观测度的影响[14-15]，为后续提高组合导航精度及其收敛速度提供了参考[16]。

1 SINS/DVL组合导航系统状态方程与量测方程

本文研究了SINS/DVL组合导航系统的可观可控性，系统主要由捷联惯性系统、Doppler计程仪、Kalman滤波器等部分组成。组合导航系统利用DVL测量的速度信息对SINS累积误差进行修正。相比GPS测量信息，DVL测量信息中仅有速度信息，组合导航系统对速度组合效果较好[17]，其具体结构如图1所示。

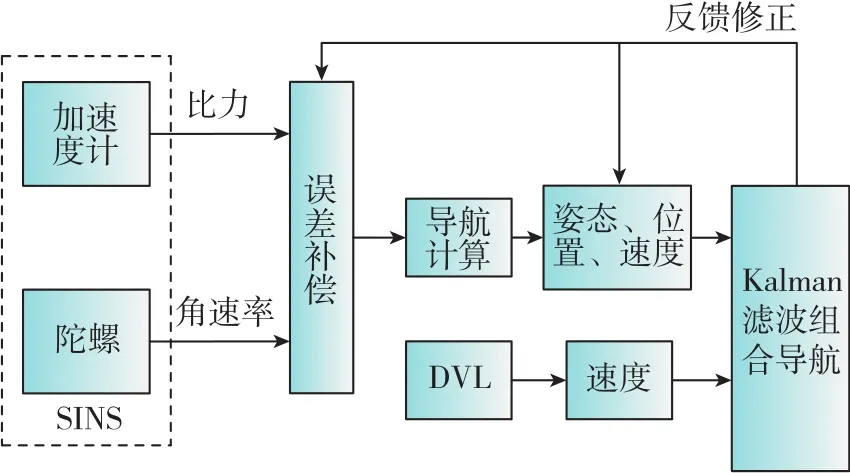
图1 SINS/DVL组合系统的基本工作原理Fig.1 Principle frame of SINS/DVL integrated navigation system

本文讨论了利用DVL速度信息进行融合的松组合系统。系统采用北天东地理坐标系，选取惯性导航系统误差及DVL相关误差项作为状态量的扩充。Kalman滤波器是针对如下线性系统建立的[18]

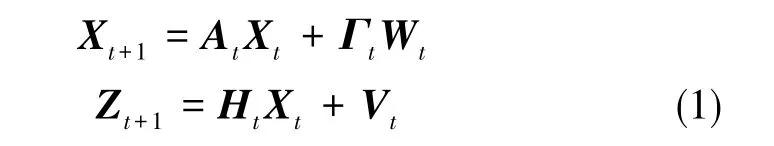
式（1）中，At为状态转移矩阵，Γt为状态量噪声转移矩阵，Wt为随机状态量噪声阵，Ht为观测转移矩阵，Vt为随机观测量噪声阵，状态量Xt为

式（2）中，δVe、 δVn分别为惯性导航系统的东向速度误差、 北向速度误差， Δφn、Δφu、 Δφe分别为北天东方位失准角，ΔL、Δλ分别为纬度误差和经度误差，εx、εy、εz为陀螺随机漂移，ΔVd为DVL速度偏移误差，δΔ为偏流角误差，δc为刻度系数误差。

r为焊点半径,取0.175 mm[13],l为代表性胞元的宽度,取0.46 mm。各材料参数如表1所示。

在SINS/DVL组合导航系统中，将惯导解算的速度与DVL测量的速度之差作为量测值

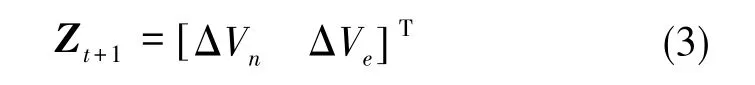
2 基于奇异值分解的系统状态可观测度分析方法

2.1 可观测性矩阵

在一个足够小的时间区间Δti（i＝1，2，…，n）内，如果线性时变系统的系数矩阵变化量可以忽略不计，那么在该段时间区间内就可以把时变系统视为定常系统并进行处理，即可以使用PWCS可观测性分析法。对于如下离散型PWCS，有

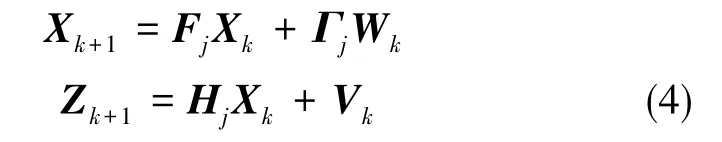
可观测性矩阵可以表示为

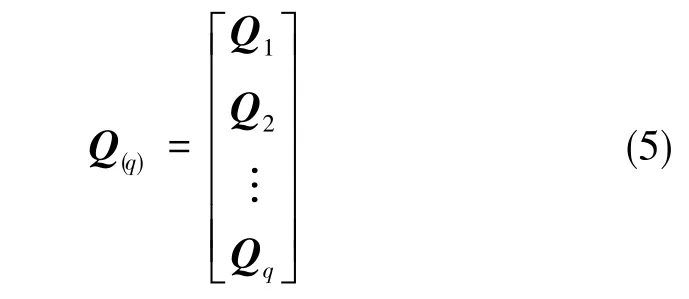
若Q（q）列满秩， 则系统完全可观测，r＝rank（Q（q））则为系统的可观测维度。

2.2 基于奇异值分解的可观测度计算

基于奇异值分解的系统状态可观测度分析方法涉及外部测量值的使用，因而采用离散系统模型较为合理。对于上述离散系统，计算第j个时间段的可观测性矩阵Q（j）， 并做奇异值分解[19]（SVD分解），即有

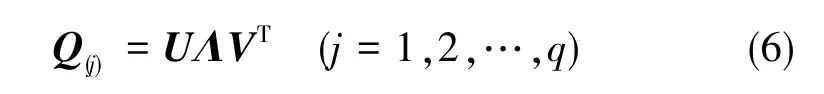
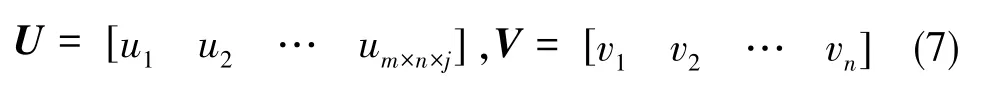
Z为整个时间段的观测值，则初始状态向量可以进一步表示为

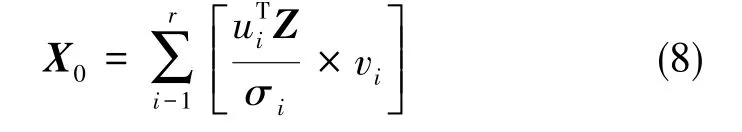
定义第k个系统状态量的可观测度为:在系统初始状态向量中使得该状态取得最大绝对值时的奇异值与具有直接外部测量值的状态量所对应的奇异值之比

式（9）中，k＝1， 2， …，n，σi为在状态向量X0，i中取得最大绝对值的状态对应的奇异值。为方便比较所有状态量在同一时刻可观测度的大小情况，本文提出了一种归一化概念:定义某一时刻所有状态量对应的奇异值中的绝对值最大者为σ0，这样就将可观测度ηk限定在了[0，1]之间，可以直观地比较各个状态量的可观测度大小。

在深入理解SVD奇异值分解的基础上，关于k的求取有如下研究结论:每一个奇异值σi都正好对应一个初始状态向量X0，i。在本文的组合导航系统中，该列向量有13个元素，取得最大绝对值的数值对应的序号下标即为k的取值，表示第k个状态量与该奇异值σi的关联度最高，可以表征第k个状态量的可观测性能。通过归一化计算，可以更直观地看出关联度的大小。

2.3 可观测性矩阵的进一步简化

由于目前的可观测性矩阵需要进行累加计算，随着可观测性矩阵维数的剧增，对其进行奇异值分解的工作量也十分巨大。因此，本文提出了一种进一步简化的可观测性矩阵的计算方法。该方法可以大大降低运算量，提高实时观测系统状态的可行性。

设分段时间间隔为q，即滤波周期每运行q拍进行一次可观测性矩阵运算，其示意图如图2所示。

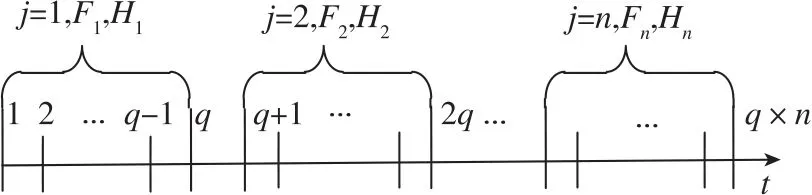
图2 可观测性分段时间示意图Fig.2 Schematic diagram of observability segmentation time

在j＝1的q拍时间段内，累加计算的可观测性矩阵为

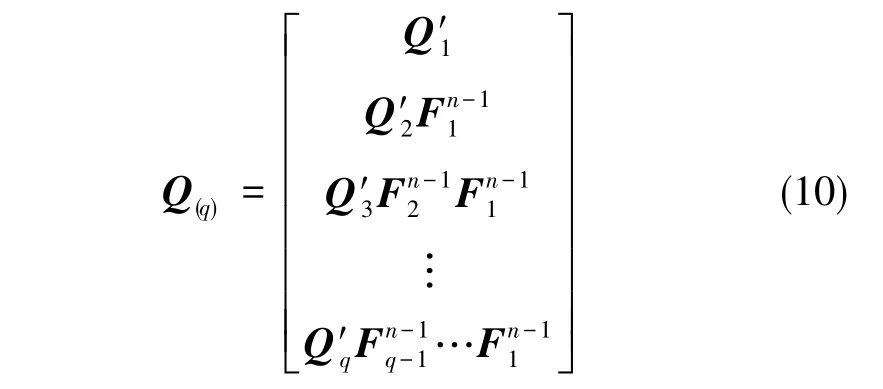
根据文献[20]提供的推导和证明可知，连续型PWCS和离散型PWCS的可观测性是等价的，离散的过程并没有损失系统的可观测度，即可以用式（11）中的替代Q（q）研究系统对应的离散系统的可观测性。

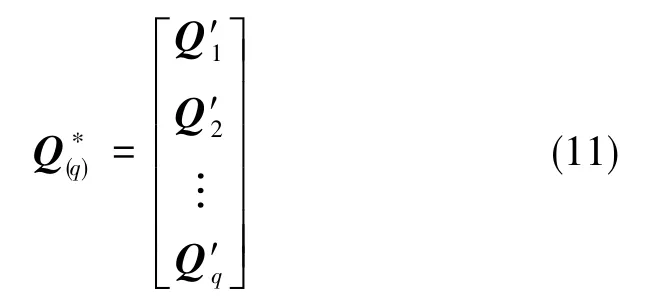
本文在的上述简化方法的基础上进一步提出了可替代的简化方法:对于在高动态状态下的运动载体而言，选取的时间段越小，越为精确。可以认为在短时间段时间q内，Fq、Hq与F1、H1相差很小，其差异可以忽略不计。因此，用Q1替代q区间上的全观测矩阵， 可以大大减少运算量，同时不会失去状态量本身的观测特性。

对于全时间段的可观测性矩阵

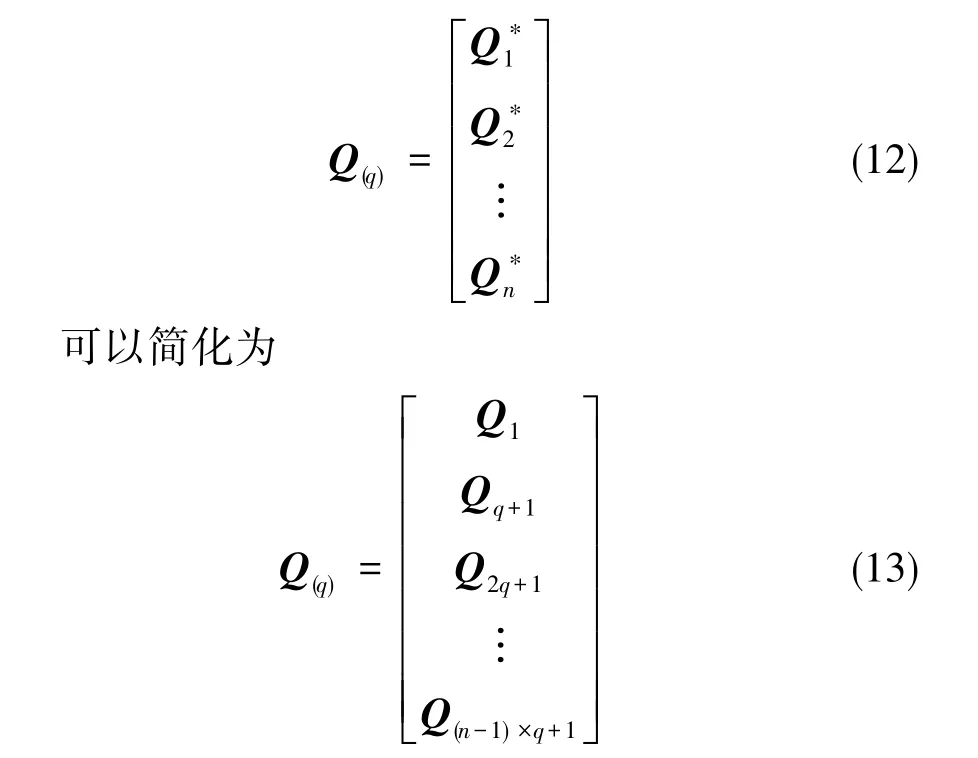
最后，根据状态矩阵的递推关系，如果每个q+1时间段的状态初始值设置为上一个q时间段的状态末值，那么随着状态矩阵的递推，可观测性矩阵仍具有累积遗传的性质。这样，Q（q）的计算便无需累加，其阶数也是恒定的，对其进行奇异值分解的运算量便大大减少了。

根据上述的简化计算，实现高动态组合导航系统长时间导航的状态可观度计算可以在工程层面实现，最后为实现全时间段每个状态量实时可观测度的比较分析，根据本文提出的归一化方法对各状态的可观测度进行了归一化处理。

3 仿真验证与分析

仿真软件为Matlab2010a，设计了一条理论无机动弹道，包含900s初始对准。设定初始姿态角为[0°0° 0°]， 初始位置为[0m 0m 0m]， 初始速度为10m/s（船头方向）， 陀螺常值漂移误差为1（°）/h，随机漂移误差为1（°）/h，加速度计零偏误差为1×10－3g， DVL 测速误差为0.001m/s（均值）， DVL 常值误差为0.0005m/s。采用上述组合导航系统，分析该系统在该单一航迹下的系统可观测度，如图3所示。在图3中，横坐标为仿真时间，纵坐标为归一化处理后的各观测参数的可观测度（是量纲为1的比值参数，0表示不可观测，1表示完全可观测）。

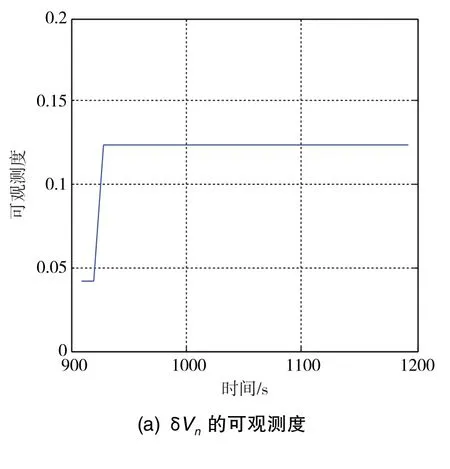
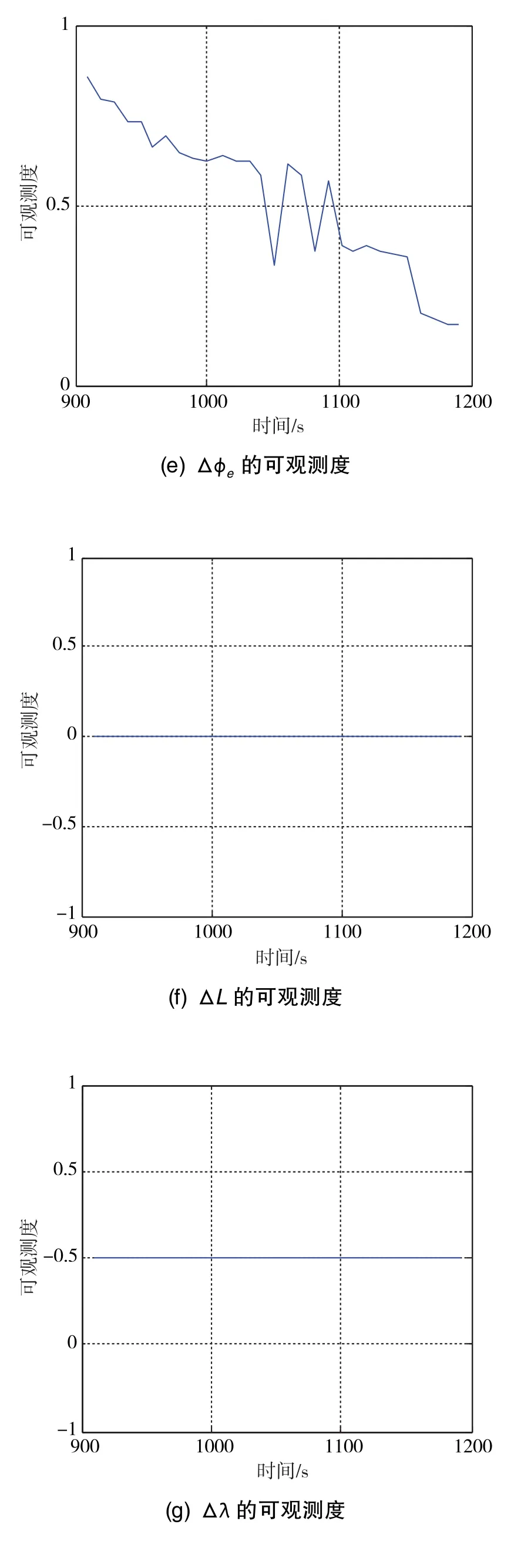
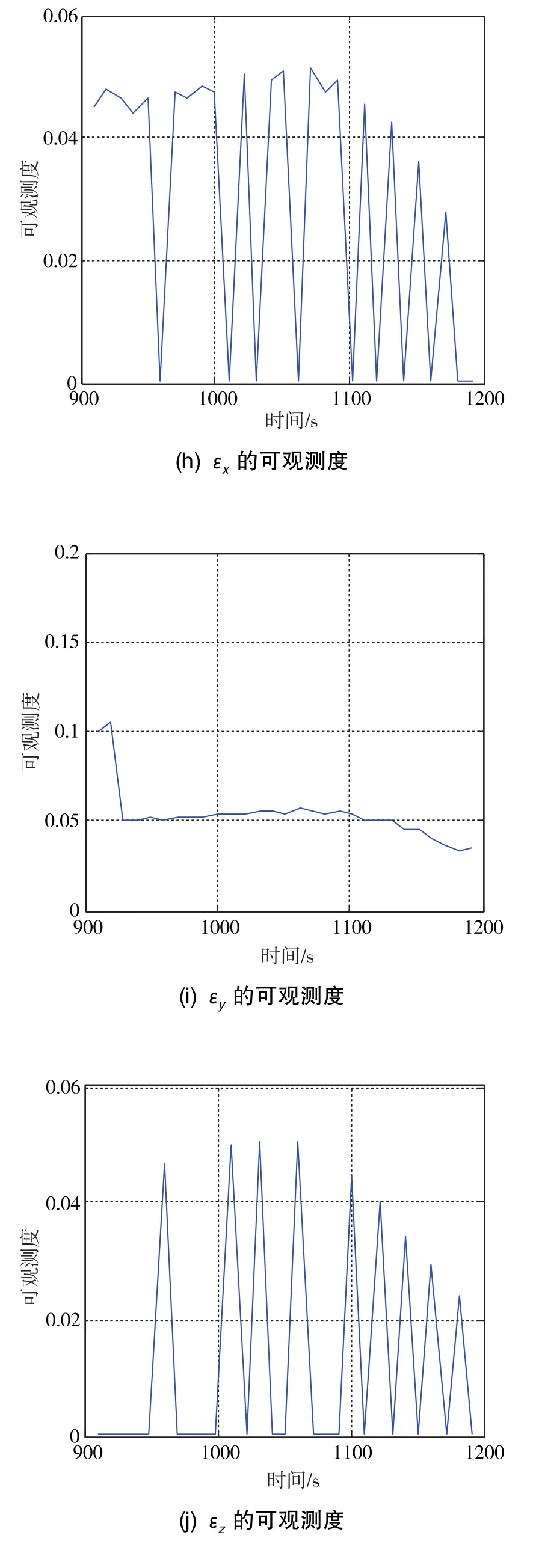
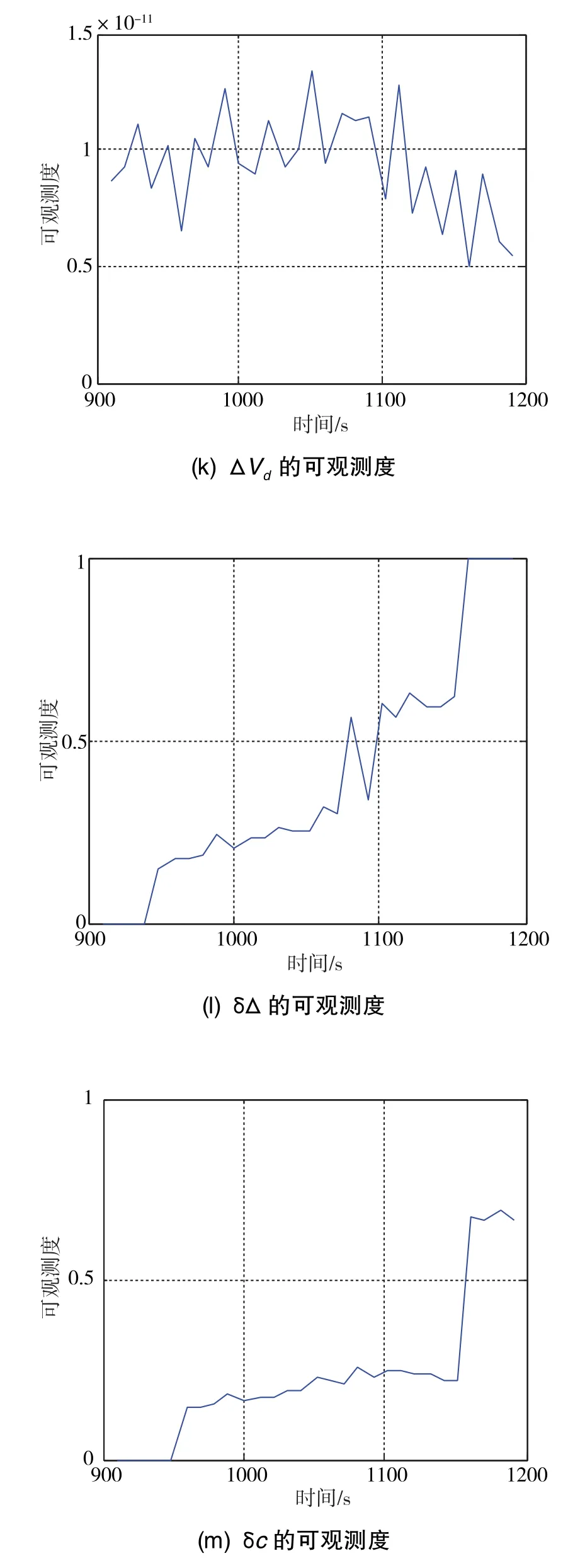
图3 各状态量的可观测度Fig.3 Observable degree of navigation states

仿真结果表明:Δφn、Δφe、δΔ的可观测度较好，具有外部观测信息的δVn、δVe具有一定的可观测度，Δφu、ΔL、Δλ、ΔVd不可观测或者几乎不可观测，εx、εy、εz的可观测度不高。

4 基于SINS/DVL组合导航系统可观测度计算的湖面实验

4.1 硬件设备

实验系统在硬件上由SINS、DVL和导航计算机构成:SINS输出陀螺测量的角速度增量累加和信息，以及由加速度计测量的视速度增量累加和信息；DVL直接输出本体速度信息，导航计算机完成数据采集、晃动基座初始对准和组合导航解算等功能。导航计算机通过1553B总线采集IMU中陀螺和加速度计的原始测量数据，数据更新频率为200Hz。DVL速度信息在导航计算机中获得提取后，与SINS的原始测量数据一起以100Hz的更新频率被送入导航计算机。最后，根据接收到的数据完成滤波的信息融合运算，同时观测各状态量的可观测度。

4.2 湖面跑船实验

本次实验在吉林松花湖上展开，将光纤惯组、DVL固联在船体上，采用不同的两组机动航迹进行解算和显示，并计算系统的可观测度。在所采用的光纤惯组中，光纤陀螺随机误差均方差为0.15（°）/h， 加速度计常值误差为 0.11mg（3σ）， 随机误差均方差为0.11mg。在图4、图5中（除航行轨迹外），横坐标为仿真时间，纵坐标为归一化处理后的各观测参数的可观测度（是量纲为1的比值参数，0表示不可观测，1表示完全可观测）。

航迹1（来回，小角度机动）的关键参数的可观测度如图4所示。

图4 航迹1的关键参数可观测度Fig.4 Observable degree of navigation key parameters based on trajectory 1

根据可观测度的计算结果分析，状态量Δφu完全不可观测；Δφn、Δφe可观测度较高，受载体机动影响，可观测度变化较大，但总体可观测性好，可以获得较高的滤波精度；δVn、δVe可观测性较好， 但小于 Δφn、Δφe， 由于载体机动的不同，可观测度也会有相应的变化，但总体可观测，并且可以获得一定的滤波精度；其余状态量的可观测度与仿真结果基本一致。

航迹2（画圈，大角度机动）的关键参数可观测 度如图5所示。

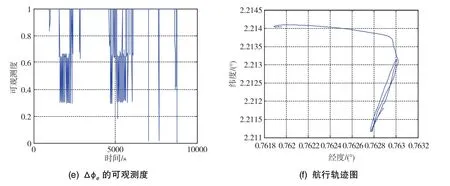
图5 航迹2的关键参数可观测度Fig.5 Observable degree of navigation key parameters based on trajectory 2

在改变了跑船机动后，对比航迹1，总体结论一致: Δφn、 Δφe可观测度较高； δVn、 δVe可观测度较好，并且相差不多，该机动方式对δVn可观测度有益；Δφu的可观测度相较航迹1变化较大，可观测度有较大提高（从几乎不可观测到在1250s～8700s之间有0.12的可观测度）；其余状态量的可观测度与仿真结果基本一致。

对比两种航迹下的位置误差（采用亚米级RTK差分导航系统作为标准弹道），如表1所示。

表1 位置误差对比Table 1 Comparison of position errors

由表1的位置精度对比可以看出，航迹2的画圈机动对组合导航的精度提高比较明显，可提高1个数量级，这与系统可观测度的分析结果完全一致，可见其对组合导航系统的指导意义。

综上所述，在实现远程导航时，可以通过不同的航迹机动来实现系统性能的提高，如本文的画圈、S机动、提速、转弯等。对飞行器而言，也可以通过抬头、加速拉升、转弯、振翼等动作提高系统的可观可控性，从而提高系统的滤波精度及收敛速度。

5 结论

本文提出了一种改进的SINS/DVL组合导航系统各状态量的可观测度计算方法，并通过数字仿真及湖面跑船实验验证了该方法可以实现滤波器状态量可观测度的实时计算。跑船实验设置了不同的航迹机动方式，验证了某些特定的机动方式可以提高系统的可观测度，从而提高了系统的滤波精度和收敛速度。在DVL的导航辅助下，组合导航的定位精度可以提高1个数量级，为后续进一步探究组合导航性能提供了参考。