北斗单点定位的误差补偿方法
2020-03-04张衡衡潘卫军殷浩然
张衡衡,潘卫军,殷浩然,刘 涛,徐 斌
(中国民航飞行学院空中交通管理学院,广汉618307)
0 引言
北斗卫星导航系统是我国独立自主研发的全球卫星导航定位系统,北斗导航系统包括空间端、地面端和用户端,可以在全世界范围内全天候地为各类用户提供高精度和高可靠的定位、导航、测量、授时等服务。1984年,我国开始筹划利用地球静止轨道卫星进行导航定位的技术方案。2018年12月,北斗卫星导航系统的服务范围扩展为全球,这标志着北斗卫星导航系统正式进入了全球时代。为了提高北斗卫星导航系统的定位精度,应尽力减小各种误差源的影响[1]。根据北斗卫星定位的工作机理,本文从影响北斗卫星定位精度的位置误差、对流层误差和电离层误差入手,提出了减少误差的修正方法。
在国内,对于精密单点定位的研究起步较晚。魏子卿[2]、葛茂荣[3]在相对定位的数学模型中也介绍了相对定位模型中非差模式的处理方法,但是这种方法和非差单点定位模式是不同的。武汉大学的叶世榕[4]对非差相位精密单点定位进行了深入研究,并且改进了模型,同时自行研制定位软件并进行了试算。目前,国际上对流层延迟现象进行改正的方法主要是模型函数法,包括Hopfield模型、Saastamoinen模型、Black模型、UNB系列模型和EGNOS模型等[5]。但是,由于对流层本身的复杂性,现存模型对于水汽在对流层空间的分布情况及其在时间上的变化规律仍然很难确切地描述。近年来,我国有学者提出组合定位的概念,利用北斗和全球卫星定位系统(Global Positioning System,GPS)共同完成伪距和载波相位组合的高精度动态定位。在对定位方法和定位系统进行研究的同时,针对北斗相关终端产品的研究也在同步进行,积极突破用户终端的解算算法,研究芯片卡板技术,制造高精度的北斗接收机,为开展北斗精确定位研究准备好前提条件[6]。
本文通过分析北斗导航系统的定位算法,对北斗导航系统的定位误差进行了研究,介绍了定位误差产生的原因,并给出了相应的减小误差的解决方案,以提高定位精度。
1 北斗导航系统的定位算法
北斗导航系统的发展经历了三代,在定位算法和误差分析上均实现了很大提升,此处介绍的是第三代北斗导航系统的定位算法。
1.1 观测方程及线性化
定义tj为卫星Sj发射测距信号的卫星钟时刻,tj(G)为卫星Sj发射测距信号的标准时刻,ti为观测站Ti接收到卫星信号的接收机钟时刻,ti(G)为观测站Ti接收到卫星信号的标准时刻,为卫星的信号传输至观测站Ti的传播时间,δti为接收机钟相对于标准时的钟差,δtj为卫星钟相对于标准时的钟差[7]。


有了线性化的观测方程,可方便地列出误差方程,进而求出观测站Ti的坐标[8]。
1.2 伪距导航原理
设在历元t时刻观测站接收机观测了n颗卫星(n>3), 相应的伪距观测量分别为, 由上述伪距观测的线性观测方程可以列出矢量表达的误差方程
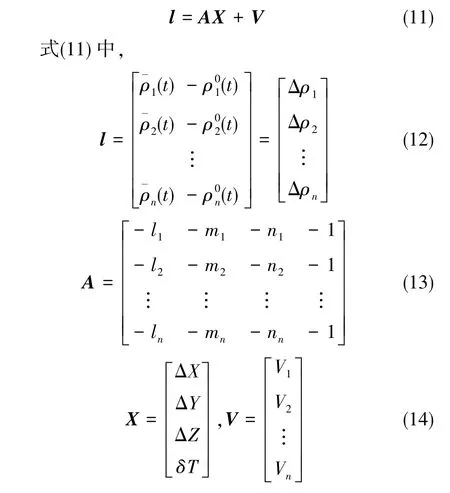
解上述方程,并且由最小二乘法可得

如果给每个观测值赋予不同的权,即对所有观测量都有权阵Q-1, 则误差方程的最小二乘解为
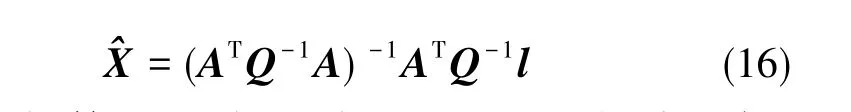
上述解算过程涉及到了观测站的概略坐标,如果观测站概略坐标与真实坐标相差较大(如相差数千米),为了获得较高的定位精度,需要一个迭代过程,直到坐标的改正量足够小[9]。
2 北斗单点定位系统误差补偿方法
对北斗系统在进行定位解算工作中的误差进行分析,其误差来源可以大致分为三个类型:1)由卫星自身相关因素引起的误差;2)由传播路径相关因素引起的误差;3)由接收机相关因素引起的误差。下面主要分析星历误差、电离层误差和对流层误差,并提出修正模型。
2.1 卫星星历误差及修正方法
卫星的理论位置和实际位置在实际情况下存在着一定的误差,即广播星历的卫星轨道误差(又称卫星轨道偏差)。GEO卫星对地球有相对静止性,在分析时很难将GEO卫星定轨时钟的卫星钟差分离开来。同时,光压对GEO卫星产生的影响较大,在其他条件相同的情况下,由GEO星历导致的测距误差约为MEO卫星的两倍。
利用改进低次曲面模型修正星历误差:利用多个差分站的星历误差在一定的服务区域内建立低次曲面模型,并将曲面模型的几个参数广播给用户。用户根据自己所处的经纬度,利用曲面模型参数计算出所在位置的星历误差,并直接改正[10]。
低次曲面模型可表征为
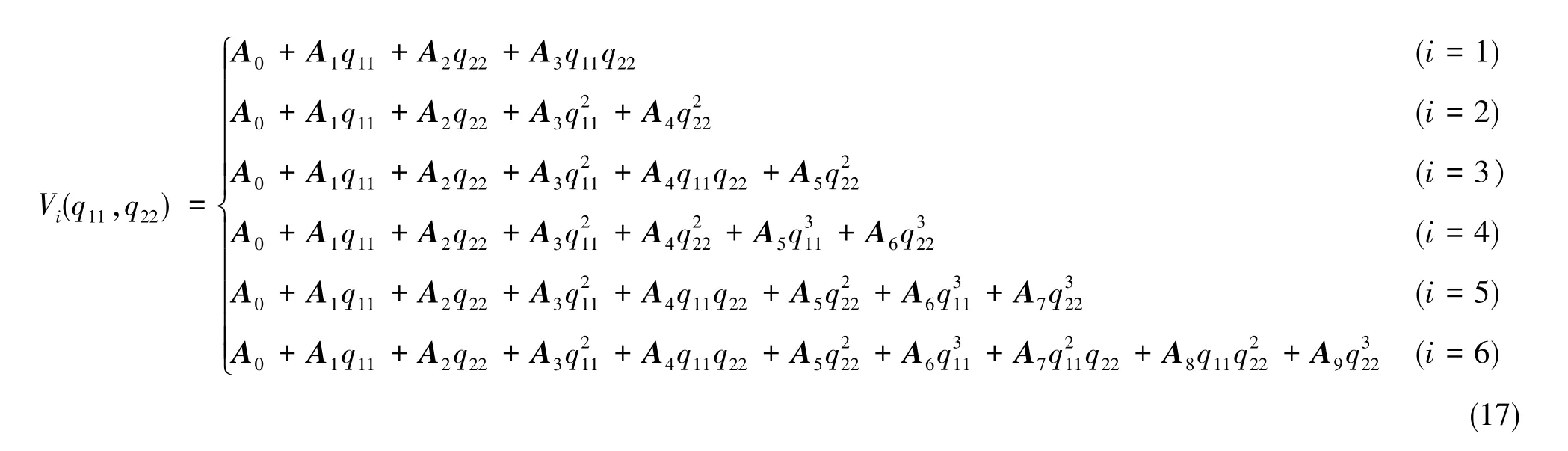
式(17)中,Vi(q11,q22)为星历误差,q11和q22分别为用户所在位置的经度和纬度,Aj(j=0,1,2,3,…,9)为第j个系数矩阵,则经过迭代后为

式(18)中,Δρ为经过修正、消除星钟差后剩余的星历误差,其模型对应的迭代矩阵D有6种形式。 式(19)以模型 2(式(17)中i=2 的情况)为例,可表示为
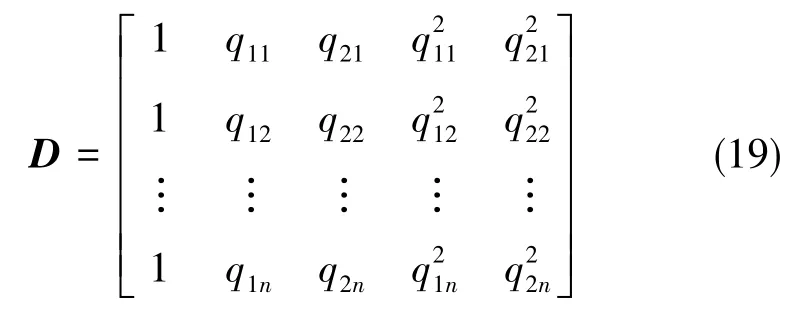
式(19)中,D的行数等于差分站数量,q1n和q2n分别为差分站n的经度和纬度。根据模型参数计算用户所在位置的星历误差

式(20)中,Du为用户所在位置对应的迭代矩阵, 其有 6 种形式。 式(21)以模型 2(式(17)中i=2的情况)为例,可表示为

式(21)中,Du的行数等于差分站数量,q1u和q2u分别为用户所在位置的经度和纬度。
改正后的残余星历误差ε=Δρ-V。
为了验证上述6种低次曲面模型的改正效果,利用6个均匀分布的差分站(位于西安、长春、上海、乌鲁木齐、三亚、拉萨)与5颗由GEO、MEO和IGSO卫星组成的混合星座进行实验。卫星1、卫星4、卫星5选用GPS中的MEO卫星,卫星2、卫星3分别选用北斗卫星导航系统中的GEO卫星和IGSO卫星,这5颗卫星在北京时间04:00~05:00对这6个差分站都是可视的,其中卫星1作为基准星,不改正[11]。在实验数据中,卫星1、卫星4、卫星5的真实星历用国际GNSS服务组织发布的精密星历代替,卫星2、卫星3的真实星历用武汉大学GNSS研究中心发布的精密星历代替,广播星历及伪距观测值来自中国科学院国家授时中心的双频接收机,采样频率为5min,通过内插让真实星历和广播星历均为1s/次。在74°E~138°E与9°N~49°N 格网范围内, 伪距误差在经过电离层误差改正、对流层误差改正、伪码噪声平滑、星钟误差一站式改正、站钟偏差消除后,剩余量为星历误差。通过曲面模型法在经度和纬度方向每隔4°计算一个改正后的残余星历误差ε,用ε的最大值εmax和最小值εmin、标准差σ和平均数εE表征模型的精度,实验结果如表1所示[12]。

表1 曲面模型改正后的残余星历误差Table 1 Residual ephemeris error after curved surface model correction
从表1可以看出:1)对GEO、MEO和IGSO这3种混合星座,曲面模型改正后的残余星历误差的均值都小于0.1m,误差的标准差都小于0.1m,这表明低次曲面模型法达到了较高的精度;2)模型3改正后,GEO、MEO和IGSO这3种混合星座卫星的残余星历误差的最大值、最小值、平均数和标准差的绝对值都是最小的,这表明模型3的改正效果最好。其中,残余星历误差小于0.15m,误差的均值小于0.06m,误差的标准差小于0.06m。
2.2 电离层延迟误差及修正方法
大气中的电离层在X射线和紫外线的强烈作用下,会导致一部分气体分子产生电离化,生成大量的自由电子。当北斗卫星的信号穿越该部分气体时,受自由电子的影响,传播速度发生改变,从而产生误差。
引用电离层修正模型Klobuchar,晚上时延为λ=5×10-9s,比较稳定;白天的电离层时延则可通过下式求得
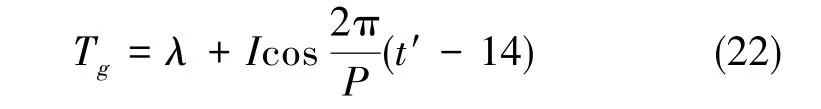
式(22)中,I为电离层时延函数振幅,单位为s;P为电离层时延函数周期,单位为s;t′为测量时刻为t时电离层穿刺点的时刻,单位为h。
对于双频接收机,由观测量组合原理可知,构造特定的双频观测量组合可以将电离层一阶误差项完全消除。伪距观测量的双频消电离层组合公式可表示为
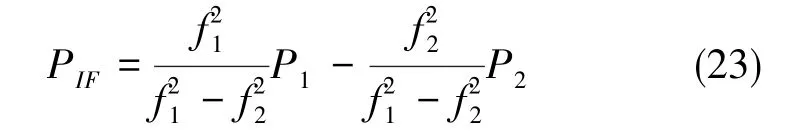
式(23)中,P1和P2分别为频点L1和L2的伪距观测量,f1和f2分别为频点L1和L2的频率。
载波相位观测量的双频消电离层组合公式可表示为
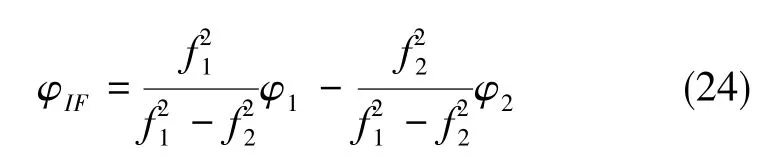
式(24)中,φ1和φ2分别为频点L1和L2的载波相位观测量。采用上述两种电离层改正方案分别对两个观测站的北斗卫星观测数据以精密单点定位模式进行解算,通过实际解算结果评估两种电离层改正方案在不同定位模式下的改正效果[13]。
通过Klobuchar模型和双频组合消电离层模型两种电离层延迟改正方法,对位于我国境内的北京和香港观测站在2019年9月9日的GPS测量数据进行分析,从而比较两种方法的修正精度[14]。表2为这两个观测站在不同电离层改正方案下不同时间的北斗卫星单点定位结果的汇总。

表2 两种电离层改正方案下的单点定位结果Table 2 Single point positioning results under twoionospheric correction schemes
利用实测GPS数据分别对Klobuchar模型和双频消电离层组合模型两种GPS电离层改正方法在定位解算时的改正效果进行评估[15],依据实验数据得到结论:在GPS精密单点定位解算时,采用双频消电离层组合模型能获得精度更高的定位结果。
2.3 对流层延迟误差修正方法
对于导航信号而言,对流层是非弥散介质,不能运用双频或三频观测来进行延迟对流层的运算工作。虽然应用差分运算可以有效减小由延迟误差造成的影响,但是差分计算只能应用于与基准站距离较近、高差较小的流动站,其在其他情况下较难获得应用[16]。
由于对流层的影响因素多,许多因素又带有较大的随机性,导致对流层延迟具有很多不规则的变化。BP神经网络通过其学习、记忆和计算等功能,可从环境信息复杂、推理规则不明确的非线性空间系统中挖掘出隐含的规律。利用BP神经网络技术可以对现有对流层延迟改正模型进行修正,进而实现对流层延迟变化的拟合。遗传算法是一种概率搜索算法,它的基本思想是通过全面模拟自然选择和遗传机制,通过对种群个体的选择、杂交和变异形成一种具有 “生成+检验”特征的搜索算法。针对BP神经网络在学习过程中容易陷入局部最小值或过度拟合的情况,可利用遗传算法的 “自适应”和 “自进化”原理,优化神经网络的初始权值和阈值,改善神经网络学习能力的可靠性和稳定性[17]。
针对目前对流层研究领域没有把遗传算法和BP神经网络技术结合应用于建立预测模型这一现象,本文在EGNOS模型基础上利用遗传算法和BP神经网络技术,消除EGNOS模型在北美洲区域的误差,建立了一种无需大量初始数据的高精度区域融合模型(GA-BPEGNOS)。
EGNOS模型是根据全球平均气象资料建立的改正模型,其纬度格网划分比较稀疏,无法准确描述小区域范围内的对流层延迟的变化规律。针对上述特点,本文通过遗传算法和BP神经网络技术,在基于EGNOS模型的基础上建立了一种高精度区域融合模型,构建融合模型的网络结构如图1所示。
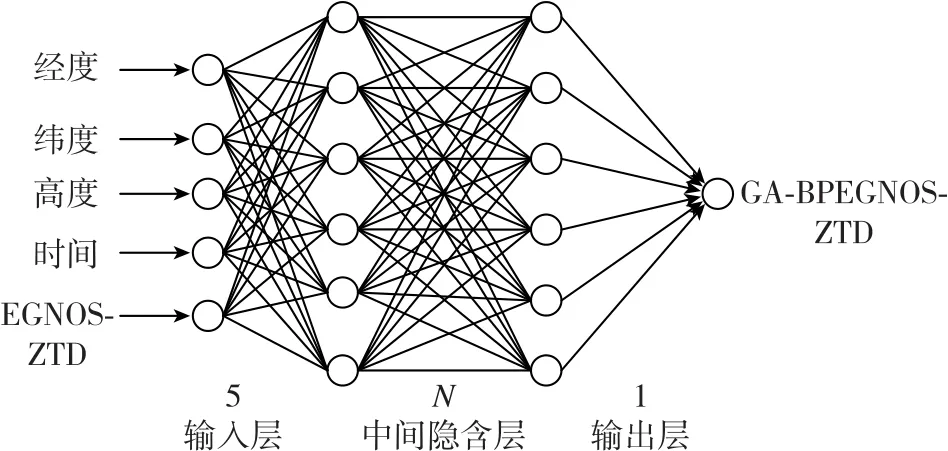
图1 融合模型的网络结构Fig.1 Network structure of fusion model
融合模型(GA-BPEGNOS)构建的具体过程如下:
1)融合模型网络的拓扑结构:构建一个5×N×1的BP神经网络模型(N为隐含层节点个数),将地面观测站的经度、纬度、高度、时间及观测站处利用EGNOS模型计算的ZTD数据EGNOS-ZTD作为输入层,输入层节点数为5;将利用遗传算法和BP神经网络技术结合模型计算出的多元线性回归延迟误差GA-BPEGNOS-ZTD作为输出层,输出层节点数为1;本文采取遗传算法和神经网络相结合的方法,将隐含层节点个数N设置为10~30,并根据每次计算输出的结果确定最佳隐含层节点个数N。
2)遗传算法:首先进行数据输入和数据预处理,然后对初始值进行编码,根据BP神经网络的适应度值。通过遗传算法中的选择操作、交叉操作和变异操作,不断优化神经网络的权值和阈值,直至满足条件。
3)BP神经网络算法:BP神经网络模型的网络参数包含学习速率η、平滑因子α、学习误差E。通过多次尝试计算,学习速率η的取值范围为[0.5,2.0],平滑因子α的取值范围为[0.4,0.9],学习误差控制E的取值范围为[0.005,0.015]。利用IGS中心提供的高精度对流层延迟产品和遗传算法得到的优化权值和阈值,对建立的BP神经网络结构进行测试。
4)融合模型对流层延迟:根据BP神经网络预测的对流层延迟残差BP-RES和EGNOS模型计算的观测站对流层延迟EGNOS-ZTD,得到融合模型的对流层延迟 GA-BPEGNOS-ZTD(GA-BPEGNOSZTD为 BP-RES和 EGNOS-ZTD之和),GA-BPEGNOS-ZTD为融合模型的ZTD,BP-RES为BP神经网络预测的对流层延迟残差[18]。
为了验证融合模型的精度,选取北美洲(10°W~160°W, 10°N~80°N)的41个观测站点, 以 IGS中心提供的2010年~2014年ZTD产品作为真值进行验证,其中包含北斗卫星定位数据。以平均偏差(BIAS)和均方根误差(RMSE)作为评价模型精度的标准,具体算式为

式(25)、 式(26)中,N为检验样本数量,为模型计算的对流层延迟值,IGS_ZTD为对流层延迟真值。EGNOS模型和融合模型计算的平均偏差(BIAS)和均方根误差(RMSE)如表 3 所示。

表3 部分检验观测站的平均偏差和均方根误差Table 3 BIAS and RMSE of some inspection stations
经上述研究,本文得出如下结论:与EGNOS模型相比,基于遗传算法和BP神经网络技术的融合模型的精度有显著提高,据所用观测站平均偏差(BIAS)和均方根误差(RMSE)的平均值计算得出的精度提高比例约为52%。
3 结论
北斗导航系统是国之重器,随着导航系统在军事领域和民用领域的广泛应用和普及,导航系统对误差精度的要求越来越高。本文首先推导了北斗卫星导航系统的定位算法,随后提出了修正星历误差的改进低次曲面模型、对比修正电离层延迟误差的Klobuchar模型和双频组合消电离层模型,以及对流层延迟误差的高精度区域融合模型,最后对北斗导航系统的定位误差进行了研究,并给出了相应的减小误差的解决方案。仿真计算的结果表明,经过修正方法修正后的定位误差明显减小,定位精度明显提高。
