嵌入式质量块对隔声门低频段隔声性能的影响∗

夏兆旺 薛 斌 许祥曦 苏战发 王宗耀 方媛媛

0 引言

伴随着人类社会的发展，低频噪声控制日益受到密切的关注。相关研究表明，长期暴露在低频噪声环境中，会对健康产生负面影响，出现心情烦躁、头晕和注意力分散等症状[1−3]。在低频段，声波波长较长，声音在传播过程中具有更强的穿透性，衰减也更缓慢。因此，低频噪声控制是声学领域的研究热点和难点[4]。噪声控制在环境声污染的治理中发挥着关键作用，在实际工程中由于房间隔墙和外墙的厚度都很大，噪声容易得到控制，而供人员出入的门口则成为噪声超标的主要场所。目前，通过安装隔声门可以很好地抑制噪声的传播。为了控制隔声门的质量、厚度和成本，隔声门采用了钢板、阻尼层和吸音棉的复合结构，通常吸音棉的厚度占有最大的比例，吸音棉的厚度影响了门的隔声有效频段。常见吸声材料的吸声能力与其厚度密切相关[5]，要在低频段达到与高频段相当的隔声效果需要更厚的吸音棉。由于隔声门整体厚度和重量的限制，隔声门在低于500 Hz 范围内的隔声效果较差。针对这个问题，研究人员提出主动控制技术来提高低频隔声效果，但是这些系统太过复杂而不适合应用在隔声门的实际使用中[6−7]。本文考虑将嵌入式质量应用于隔声门中来提高低频段的隔声性能，同时保证隔声门在高频段仍有很好的隔声效果。

嵌入式质量是一个个任意形状的质量块，将嵌入式质量加入吸音棉中可以有效改善吸音棉在低频段的隔声量[8]。在吸音棉中加入嵌入式质量后，这些质量块与吸音棉组成了多个“质量-弹簧-阻尼”系统。在这些系统中，吸音棉可视为系统的刚度和阻尼元器件，嵌入式质量可视为质量元器件，整个系统结合了高频阻尼吸收能量和低频动力吸收能量的机理。合理设计的嵌入式质量块，可以通过其低频共振来调谐系统的振动，从而用于控制低频噪声[9]。目前，一些学者已经研究了嵌入式质量的应用，Idrisi 等[10]实验探究了各参数对加入嵌入式质量后系统固有频率的影响，总结了质量块的质量、质量块间的距离和形状等参数的影响规律。Slagle[11]通过建立阻抗管的有限元模型(Finite element model, FEM)分析了质量块的材料、大小、形状和放入深度等参数对隔声量的影响。本文将嵌入式质量应用在隔声门中，建立了混响室有限元模型计算隔声门的隔声量，对各相关参数进行了参数关联性研究并对整个系统在低频段的有效隔声量进行了优化设计。

1 隔声门隔声性能优化基础

1.1 隔声量计算

如图1所示，声音从声源室经过隔声门传入接收室，声源室内平均声压级为L1，接收室内平均声压级为L2，

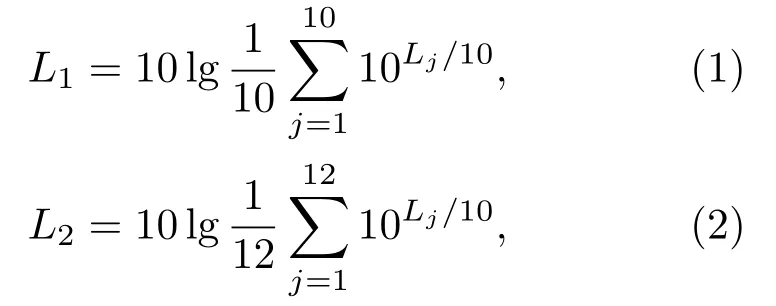
其中，L1,L2,··· ,Ln为室内不同位置测点处的声压级。

已知L1和L2后，代入式(3)求得隔声量：

式(3)中，S为隔声门的投影表面积，m2；A为接收室的有效吸声面积，m2。

为了计算有效吸声面积，本文将接收室的所有墙壁表面吸声系数设置为0.008，根据赛宾公式算出混响时间为13.057 s，然后将混响时间代入式(4)中可以计算出有效吸声面积：

式(4)中，V为接收室的体积，m3；T为混响时间，s。

图1 隔声门隔声量计算模型Fig.1 The model used to calculate the transmission loss of the soundproof door

1.2 遗传算法理论

为了得到加入嵌入式质量后隔声门隔声性能的最优值，后文使用遗传算法对此问题进行分析求解。遗传算法是基于达尔文的自然选择理论提出的优化算法，该算法在对实际问题进行优化的过程中涉及选择、交叉和变异环节[12]。以下结合后文研究内容简要介绍遗传算法的应用。

首先算法在嵌入式质量的相关参数的取值范围内进行取值，生成具有一定个体数的初始种群，种群中的个体表示各相关参数(即本文的输入参数)取值后组成的特定解，而个体组成的种群为在各输入参数范围内取不同值时组成的特定解的集合。有了初始种群，算法会根据适应度函数计算出每个解集所对应的适应度，上述适应度函数即为后文的设计目标(见3.3节)。大自然中，具有生存优势的种群或种群中的个体更容易繁衍下去。同样，遗传算法根据适应度对所有的可能解(种群中的个体)进行选择，并按照适应度越高、选择概率越大的原则，从种群中选择两个个体作为父方和母方。选择算法一般使用Roulette Wheel算法：假设有n个个体，他们所对应的适应度值分别为f1,f2,f3,··· ,fn，则第i个个体被选中的概率为

式(5)中，i=1,2,··· ,n。

选择出两个个体后就要交叉生成新个体，记这两个个体为Parent1 和Parent2，生成两个新个体为Offspring1和Offspring2：

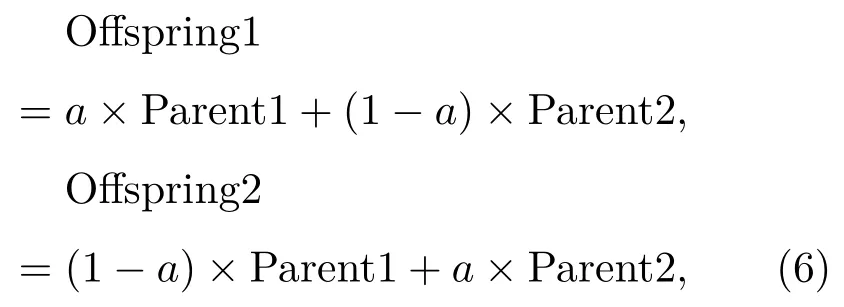
式(6)中，a为交叉概率。

生成新的个体后，继续考虑变异对该个体的影响：

式(7)中，UpperBound为取值上限，LowerBound为取值下限，C为变异后的个体，P为变异前的个体，δ为由多项式分布计算得出的小量。

对初始种群中的个体重复进行上述选择、交叉和变异过程直至生成的新个体数达到用户设置的每次迭代个体总数。再将上述生成的所有新个体组成新的种群，对这个新种群进行选择、交叉和变异生成下一个种群，重复上述过程直至生成的种群代数达到设置的种群迭代数。本文设置初始种群中的个体数为8500 个，每次迭代个体总数为5500个。

2 隔声门隔声性能分析建模

2.1 混响室建模

按照国际标准ISO 10140 的要求建立了两个相邻混响室的有限元模型以计算隔声门的隔声量。由于低频时声波的波长较长，要获得准确的结果需要具有更大空间的混响室。为了保证结果准确的同时分析模型又不至于太大，确定两个混响室的尺寸如表1所示。

表1 混响室尺寸Table 1 Dimensions of the reverberation room

为了增强室内的低频散射声场，在声源室和接收室顶部以及四面墙上随机布置了4 种不同直径的半球形体[13]。与其他形状相比，使用半球形体后室内的散射声场会更加均匀。最终的混响室模型如图1所示。

2.2 声源和测点位置的确定

按照ISO 10140-5 的附录D 提出的建议在声源室中选取合适的位置布置声源。在低频段，室内的声场并不是完全散射的，隔声量的计算结果受声源位置的影响很大，本文结合ISO 10140-5 提出的要求选取了38 个不同的声源位置来提高计算精度，各声源间距离不少于1 m，声源中心距离各墙面距离均大于0.7 m，任意两个声源确定的平面都不与墙面平行且所有声源都不在声源室的对称面上。模型中所有声源均为全向声源，单个声源如图2所示。

图2 全向声源Fig.2 Omnidirectional sound source

与声源的布置原则相似，测点的位置也要满足以下要求：测点位置应尽量分散开以便布满整个室内空间；各测点间距离均大于1.2 m；所有测点与墙面距离均大于1.2 m；测点与被测隔声门表面的距离不小于1.2 m；测点距离声源不小于1 m；声源室和接收室内的测点数不少于6 个。以上要求为最低原则，在满足条件的情况下应尽量取最大值。本文分析模型中声源室内测点数为10个，接收室内测点数为12个。

2.3 隔声门建模

声源室和接收室通过隔声门连接。实际实验室测量隔声量时构件被固定安装在测试洞口内，本文通过约束隔声门4 个侧面钢板的平动自由度来模拟实际测量的边界条件。隔声门高2100 mm，宽1000 mm，厚100 mm，从声源室一侧到接收室侧分别为2.5 mm 厚钢板、2 mm 厚阻尼板(三元乙丙橡胶)、玻璃棉、2 mm 厚阻尼板和2 mm 厚钢板，嵌入式质量被放置在玻璃棉中。为了控制变量数目和便于参数化，本文选取了12个长宽高均相同的长方体形状的质量块，按每层4 个、一共3 层放置在玻璃棉中。隔声门如图3所示。

图3 加入嵌入式质量后的隔声门示意图Fig.3 Schematic diagram of the soundproof door with embedded masses

3 影响参数的关联性研究

3.1 质量块材料的影响

分别将铝合金和铸铁作为嵌入吸音棉中质量块，分析质量块的材料对低频段隔声量的影响，结果如图4所示。

由图4可知，质量块主要在低于50 Hz 的频段内起作用，质量块的材料对低频隔声特性有较大影响，在20～250 Hz频段，铸铁材料的隔声量比铝合金材料的隔声量增加了4.1 dB。随着质量块密度的增加，隔声量曲线的低频波谷向低频移动且波谷的值变大。

图4 不同材料的质量块对隔声量的影响Fig.4 Effect of changing the material of embedded masses on the transmission loss

3.2 质量块与隔声门底部距离的影响

其他参数不变，改变第一层质量块与隔声门底部的距离(图6中的P9)，分析其对隔声门低频段隔声量的影响，结果如图5所示。

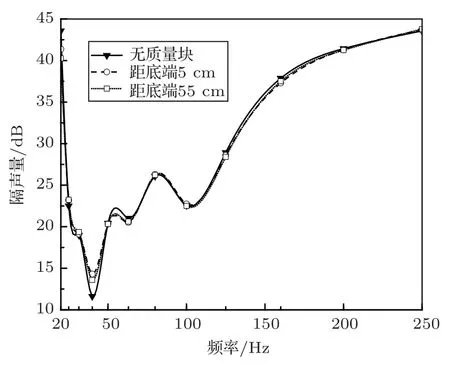
图5 质量块与隔声门底端距离对隔声量的影响Fig.5 Effect of changing the distance between embedded masses and the bottom of the soundproof door on transmission loss

由图4和图5可知：与质量块的密度相比，质量块与隔声门底部的距离对低频隔声的影响较小，因此需要找出对隔声门的低频隔声有较大影响的参数，便于后续的优化设计。

3.3 设计目标

为了找出主要影响参数，本文首先对可能影响隔声门低频段隔声性能的参数进行参数关联性分析。在进行关联性分析及后续的优化设计之前，需要首先确定设计目标。已有研究表明：评价低频成分占主导或低频声压级较高的噪声时，A 记权声压级、响度等常用指标的评价结果并不准确。因此，如何建立一个准确的低频段噪声评价方法，仍是目前学者们努力的方向。本文基于一种建筑结构低频有效隔声量评价方法(Tokita 记权有效隔声量)，对模型的计算结果进行分析和评价[14]。此方法与ASTM E413-10 中的评价方法类似，主要区别如下：(1)两者适用的频率范围不同；(2)两者使用了不同的记权值。此评价方法结合Tokita阈值提出的记权值可更好地评价结构的低频段隔声效果，Tokita 阈值考虑了低频噪声对人体的干扰特点，提出人体对不同频率下噪声的敏感度不同，已被证实可以较好地表征人对低频噪声的主观感受[15]。本文使用的记权值如表2所示，使用此记权值可得到隔声门的Tokita记权有效隔声量。

结合以上记权值和Tokita 记权有效隔声量的确定方法可以计算得到本文的设计目标，具体方法可查阅参考文献[15]。

表2 Tokita 记权值Table 2 Reference sound insulation contours for calculation of weighted sound transmission loss

3.4 输入参数与设计目标的关联性

本文考虑的参数一共有15 个，用P1 到P15 来表示所有参数。其中P1为质量块宽度；P2为质量块长度；P3 为质量块高度；P4为质量块与靠近接收室一侧阻尼板的距离；P5为质量块与侧板的距离；P6、P7 和P8 为各个质量块之间在x方向的距离；P9 为最底层质量块与玻璃棉底端的距离；P10 和P11 为各个质量块之间在y方向的距离；P12 为质量块密度；P13 为质量块杨氏模量；P14 为质量块泊松比；P15为Tokita 记权有效隔声量。其中所有质量块的尺寸都相同且第二层和第三层的质量块的位置由第一层质量块平移得到，这样可以进一步减少变量数目，上述各参数见图6。其中各输入参数的取值范围见表3，所有参数的单位均为国际单位制SI。

确定设计参数后，在ANSYS DesignModeler中参数化所有几何参数，即P1、P2、P3、P4、P5、P6、P7、P8、P9、P10 和P11；在工程数据面板中参数化材料参数，即P12、P13和P14。由于ANSYS在声学分析中只提供了一些常见声学结果的后处理工具，无法直接输出上述设计目标(Tokita 记权有效隔声量)，本文通过编程实现了Tokita 记权有效隔声量的输出和参数化。参数化完成后，首先在优化设计模块中完成参数的关联性分析。进行参数关联性分析的主要目的是剔除次要影响参数，本文的设计参数很多，采用直接有限元计算的方法进行优化设计耗时太长，因此后续进行优化设计时采用了响应面的方法。通过对所有参数的所有可能取值进行实验设计(Design of experiment, DOE)抽样，利用响应面技术对所有样本的计算结果进行拟合。为了保证拟合精度，设计参数越多就需要更多的样本数，因此进行参数关联性分析是很有意义的。

图6 用于参数关联性分析的参数示意图Fig.6 Parameters used to do the parameter correlation study

表3 各输入参数的取值范围Table 3 Ranges of input parameters

进行参数关联性分析需要的样本数必须大于设计参数的个数，本文选取了23 个样本进行计算。各输入参数(P1至P14)与输出参数(P15)的相关性如图7所示。

图7 输入参数与输出参数的相关程度Fig.7 Correlation between input parameters and output parameters

图7中相关度为1 表示关联程度最高，0 表示无关联，可以看出P6 与输出参数P15 关联度最大，P8和P12 也与P15 有较大的关联性，P10 与P15 的关联性最低，因此可以考虑在后续的优化中去除此输入参数。由于本文进行参数关联性研究时只使用了23个样本，样本数偏少可能导致关联性结果偏离实际，所以后续进行优化时仍保留了大部分的输入参数。参数P4为隔声门厚度方向的一个变量，其取值范围很小，因此去除了此参数；此外，实际物质的密度、杨氏模量和泊松比不可能随机取值，确定一种物质后其密度、杨氏模量和泊松比就确定了，因此本文去除了参数P13和P14而保留了与设计目标更有关联性的参数P12。

4 隔声门低频段隔声性能优化

如第3节所述，本文去除了参数P4、P13和P14，保留了其他参数，同时为了控制隔声门的质量，添加了单个质量块的质量用作本节优化的约束条件。参数P4取定值0.02 m(见图8)。重新对这13个参数进行排序，记为P1′, P2′, P3′,··· ,P13′。其中P1′为质量块的宽度；P2′为质量块的长度；P3′为质量块的高度；P4′为质量块与隔声门侧板的距离；P5′、P6′和P7′为各个质量块之间在x方向的距离；P8′为最底层质量块与玻璃棉底端的距离；P9′和P10′为各个质量块之间在y方向的距离；P11′为质量块的密度；P12′为单个质量块的质量；P13′为Tokita记权有效隔声量。P1′到P11′为输入参数，P12′和P13′为输出参数且P12′为约束条件。上述所有输入参数的取值范围列于表4，所有参数的单位采用国际单位制。各几何设计参数示意如图8所示。

本文设计参数多，使用直接优化方法并不现实，而使用响应面方法进行优化设计可以准确高效地找出设计空间的全局最优解。响应面技术使用DOE抽样对所有参数的设计空间进行随机取值，根据所取样本点的计算结果拟合输入和输出的函数关系，因此后续的优化并不是针对原始有限元模型的计算，而是针对拟合的函数进行计算找出最优解，这显著提高了分析模型的计算效率。使用响应面需要注意的是拟合的精度，其与下面几个因素有关：(1)分析模型的复杂程度；(2)DOE 抽样的样本数；(3)使用的响应面类型。本文共有13 个参数，在DOE 抽样时使用了151 个样本来提高响应面的拟合精度。

图8 用于优化设计的参数示意图Fig.8 Parameters used to optimize the transmission loss

表4 用于优化的各输入参数取值范围Table 4 Ranges of input parameters used for the optimization

经过计算，上述151 个样本的Tokita 记权有效隔声量的平均值为18.3 dB，得到所有样本的计算结果后需要选择合适的响应面类型进行拟合，本文选择了3 种响应面对样本进行拟合，分别为Genetic Aggregation、Full 2nd Order Polynomials 和Non-Parametric Regression。为了验证3 种响应面的精度，重新选择了两个样本进行计算，将有限元模型(FEM)的计算结果与拟合结果对比选取拟合精度最高的响应面用于优化。最终结果如图9所示，从图9中可以看出非参数回归响应面(Nonparametric regression)的拟合精度最好，而由于本分析模型较复杂，输入参数与输出参数具有明显的非线性，所以用二次函数响应面无法精确描述输入和输出的关系。

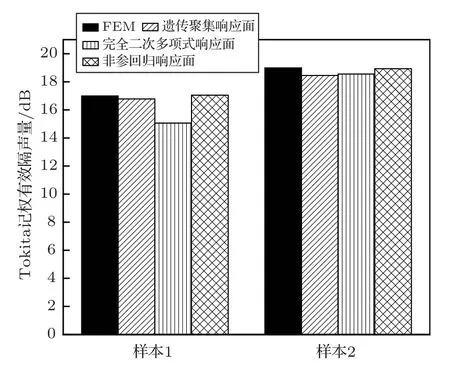
图9 响应面拟合结果与FEM 结果的对比Fig.9 Comparison of the results generated by response surface with that generated by FEM

将非参数回归响应面拟合出的输入参数和输出参数的函数关系用于最终的优化，非参数回归拟合出的某个响应面如图10所示。图10表明了参数P1′、P2′与P13′的关系，其他参数的取值如下：P3′为0.03 m，P4′为0.15 m，P5′为0.07 m，P6′为0.04 m，P7′为0.12 m，P8′为0.13 m，P9′为0.2 m，P10′为0.3 m，P11′为2300 kg/m3。

图10 非参数回归响应面Fig.10 Non-parametric regression response surface

对隔声门低频段的隔声性能进行优化，输出参数为P12′和P13′，优化目标是取P13′的最大值，约束条件是P12′ <0.4 kg，本文使用多目标遗传算法(Multi-objective genetic algorithm, MOGA)对此优化问题进行求解。多目标遗传算法对离散和连续输入参数均适用，支持对多输出问题进行优化且优化结果为全局最优，因此，选用多目标遗传算法可以很好地解决本文隔声门低频段隔声性能的优化问题。多目标遗传算法同样需要考虑精度问题，要获得准确的最优解需要合理设置算法参数，本文设置初始种群中的个体数为8500个，每次迭代时种群个体数为5500 个，初始种群中个体数越多，找到最优输入参数取值区间的概率越大。

经过优化，与未加入嵌入式质量的隔声门相比，嵌入式质量隔声门的Tokita 记权有效隔声量增加了5.0 dB。其中，未加入嵌入式质量的隔声门为16.4 dB，加入嵌入式质量后增加至21.2 dB。优化算法选取的质量块的材料为灰铸铁，其密度为6700 kg/m3，此时12 个质量块的总质量为3.5 kg。优化后各几何参数的值见表5，优化前与优化后隔声门的隔声量如图11所示。

表5 优化后各几何参数的取值Table 5 Values of geometric parameters after optimization

将优化前后隔声门的隔声量进行对比，从图11中可以看出，优化前隔声门在40 Hz 时隔声量最低，为11.6 dB，而从Tokita记权值可知人体对40 Hz处的低频噪声更敏感，因此对于本文研究的隔声门而言，对其进行低频段隔声性能的优化就是提高其在40 Hz时的隔声量。优化结果与预期一致，优化后的隔声量在40 Hz时有所改善，增加了5.5 dB。经过优化的隔声门在大于40 Hz 的较高频段内的隔声量与原隔声门相当，仍有较好的隔声效果。

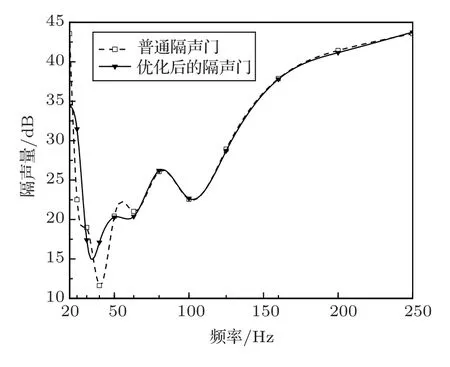
图11 普通隔声门与优化后隔声门的隔声量Fig.11 Comparison of the transmission loss between the regular soundproof door and the optimized soundproof door

5 结论

本文研究了将嵌入式质量用于提高隔声门低频段的隔声性能，建立了两个相邻混响室有限元分析模型计算隔声门的隔声量，并利用分析模型对嵌入式质量的相关参数进行了优化设计。针对低频段分析隔声量的要求，按照ISO 标准对分析模型进行了调整，选取了合适的声源和测点。通过将Tokita记权有效隔声量用作设计目标，首先对嵌入式质量的所有参数进行了参数关联性研究，结果表明各质量块在隔声门宽度方向(x方向)的距离和质量块的密度与设计目标更具有相关性。

在本文对隔声门低频段隔声性能的优化中，结合了响应面技术和多目标遗传算法对设计目标进行了优化设计，结果显示：对于所研究的玻璃棉(厚度92 mm，容重24 kg/m3)，使用灰铸铁作为质量块，并合理布置各个质量块的大小和位置可以有效提高隔声门的低频隔声性能。与普通隔声门相比，嵌入式质量隔声门的Tokita 记权有效隔声量增加了5.0 dB。