一种基于多时间尺度FFRLS-AEKF算法的动力电池SOC估计方法

宋伟　王洁　彭锦旗　张涌　张福明

摘 要：针对目前电池荷电状态（SOC）估计算法在硬件处理单元中计算量大，耗费资源多的问题，提出在SOC估算中增大参数辨识尺度，利用带遗忘因子的递推最小二乘法对电池参数进行估计。与此同时，利用自适应扩展卡尔曼（AEKF）算法对电池进行SOC估计，使算法估计结果可随噪声统计特性变化而自适应更新，实现了电池模型参数与状态的联合估计，在此基础上研究不同时间尺度对SOC估算的影响，仿真结果显示：随着辨识尺度的增大，SOC估算精度也会随之下降，计算时间减少，在权衡考虑估算精度和计算消耗时间的条件下，可找到一个最优时间尺度在既保证SOC估算精度的同时减少硬件的计算量。

关键词：锂离子电池 荷电状态 最小二乘法 自适应扩展卡尔曼滤波法

A Method of Power Battery SOC Estimation Based on Multi-time Scale FFRLS-AEKF Algorithm

Song Wei Wang Jie Peng Jinqi Zhang Yong Zhang Fuming

Abstract：Aiming at the problem that the current battery state of charge （SOC） estimation algorithm is computationally intensive and consumes a lot of resources in the hardware processing unit， it is proposed to increase the parameter identification scale in the SOC estimation， and use the recursive least squares method with forgetting factor. The battery parameters are estimated. At the same time， the adaptive extended Kalman （AEKF） algorithm is used to estimate the SOC of the battery， so that the algorithm estimation result can be adaptively updated with the change of the noise statistical characteristics， and the joint estimation of the battery model parameters and state is realized. Studying the influence of different time scales on SOC estimation， the simulation results show that as the identification scale increases， the SOC estimation accuracy will also decrease， and the calculation time will decrease. Under the conditions of weighing the estimation accuracy and the calculation time， it can be found that the optimal time scale reduces the amount of hardware calculation while ensuring the accuracy of SOC estimation.

Key words：lithium ion battery， state of charge， least square method， adaptive extended Kalman filter method

1 引言

電池模型是参数估计和SOC估算的基础，常见的电池模型为阻容等效电路模型及其改进形式。目前常见的电池模型参数估计方法包括离线辨识和在线辨识两种，离线辨识方法在电池老化或工作状态改变的情况下会导致估算精度下降，在线辨识方法可以根据实时测得的电池电流电压计算模型的参数，可针对电池老化和不同工作情况下，实现SOC准确预测[1][2]。

递推最小二乘法（RLS）是最常用的在线参数辨识方法，但递推最小二乘法的记忆长度是无限的，随着递推次数的增加，旧数据所占的比重会逐渐增多，使得新数据难以起到修正作用，造成估计效果减弱，影响对其后的参数估计效果，这种情况在时变系统中估计效果会更差。为了避免上述情况的发生，本文使用带遗忘因子的递推最小二乘法（FFRLS）来经行参数辨识。

电池模型参数辨识和电池SOC估算往往是在同一时间尺度下进行的[3]，但在SOC估算中，时间尺度较小会导致处理器运算量大，同时考虑SOC是迅速变化的量。因此，为减少处理器计算量，提出增大参数辨识时间尺度，本文基于二阶RC等效电路模型，使用FFRLS-AEKF算法探究不同辨识时间尺度对SOC估算影响。

2 等效电路模型建立

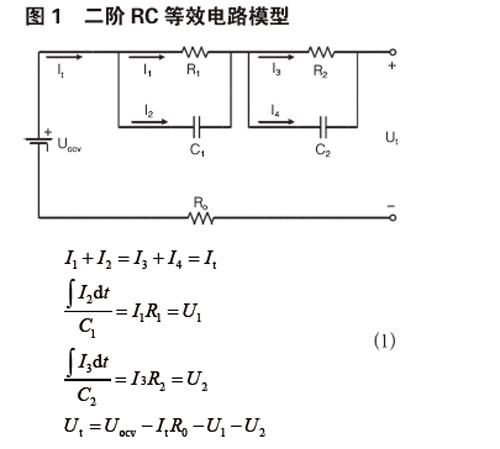
本文选用二阶RC等效电路模型来模拟锂电池动态特性，电池模型具体如图1所示。

其中，R1是电化学极化电阻，C1是电化学极化电容，R2是浓差极化电阻，C2是浓差极化电容，由基尔霍夫定律，建立电池模型数学方程。

由电路原理 KCL定律，得到关于电流的数学方程如下：

（1）

3 基于FFRLS参数在线辨识

递推最小二乘法是基于最小二乘法衍生出的递推算法，是电池模型参数辨识最常用的方法，带遗忘因子的递推最小二乘法是在递推最小二乘法中加入遗忘因子，这样可降低矩阵P（k）中的旧数据的占有量，从而防止RLS算法出现数据饱和现象，从而得到更为精确的辨识结果，FFRLS递推公式如下：

（2）

式（2）中为算法的增益矩阵，为算法的协方差矩阵，为k时刻系统的参数矩阵为FFRLS遗忘因子系数，的取值范围为0.95-0.99之间。

参数辨识的前提是获取电池的SOC-OCV曲线，通过电池充放电SOC-OCV实验，将SOC从0～100%的11个点采用6阶曲线拟合，求得平均之后SOC-OCV的关系方程为

（3）

式中：Uocv为电池开路电压。

将等效电路模型改写为离散化时间序列形式

（4）

令

式（4）整理为：

（5）

离散化后有：

（6）

其中

式中k為采样序列时刻信号，二阶RC模型中的参数可从k1-k5中推导得出。

再令

则有

（7）

进而求得：

（8）

3.1 参数辨识结果分析

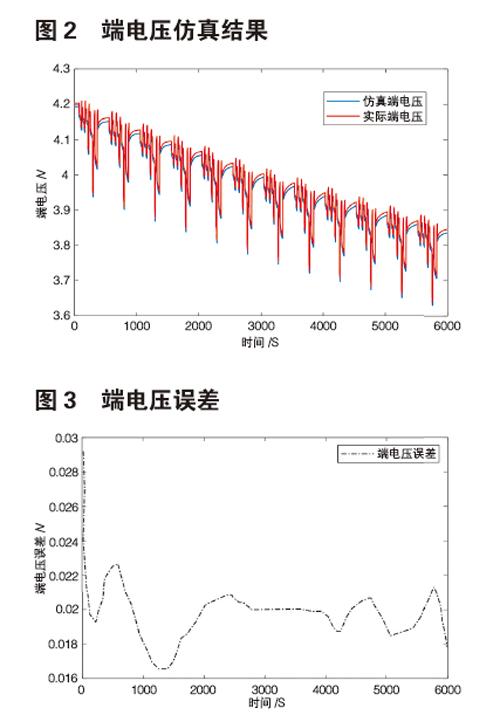
运用FFRLS进行参数辨识时，根据辨识经验，本文中遗忘因子设为0.98。选用18650电池为研究对象，其额定容量为2AH，充放电截至电压为4.2V和2.6V，取电池在DST工况下的放电结果。将参数的辨识结果的输入到二阶RC模型中，得到仿真端电压，再将其与实际的端电压对比，如图所示：

由图2和图3知，由FFRLS辨识出来的参数带入等效电路模型中得到的端电压值与真实端电压值十分接近，误差小于3mv。由图3可以看出，误差较大的时刻在仿真初始阶段，这是因为模型参数初值选取有较大偏差造成的，但在辨识中后期各参数的辨识值变得较为平缓，误差也在逐渐减小。 说明FFRLS算法在动态工况下的辨识效果是可靠的。

4 基于AEKF算法的SOC估算

传统安时积分法电池SOC计算公式（9）为

（9）

4.1 AEKF算法流程

卡尔曼滤波（Kalman filter，KF）是一种通过闭环控制来实现状态变量的最优估计方法[4]，但KF只适用于线性系统，扩展卡尔曼滤波EKF用于解决非线性系统的估计问题，然而EKF也有局限性，它将系统的噪声假设为固定不变的高斯白噪声，对于噪声统计特征未知的系统，依旧会产生误差，电池的系统噪声和观测噪声并不是正态分布的，因此噪声特性的变化对于EKF估算SOC也会造成影响，Sage和Husa建立的线性离散系统，提出了一种自适应噪声统计特性的估计方法，即AEKF[5]，流程如下：

对于电池系统，其系统方程和观测方程为

（10）

联合式（1）和（9）进行离散化处理，得到电池等效模型的状态方程：

a、初始值设置：

（12）

b、先验估计、测量矩阵更新及误差协方差矩阵更新：

（13）

c、卡尔曼增益计算：

（14）

d、当前时刻状态变量最优估计值、更新协方差矩阵：

（15）

e、自适应噪声协方差更新：

（16）

式中：代表k时刻状态变量的预测值，代表k时刻状态变量的最优估计值;Qk和Rk分别为系统噪声ωk和观测噪声νk的协方差;Pk为误差协方差矩阵;Kk代表卡尔曼增益。

5 基于FFRLS-AEKF的模型参数与状态联合估计

在确定初始值SOC（0）、P（0）、U1（0）、U2（0）、、d、θ（0）、Q（0）、R（0）后，即可根据式（2）开始实时辨识模型参数，然后将参数代入式（12）～（16）即可开始估算状态变量矩阵，由式（11）知矩阵第1行的值就是SOC。

5.1 建模仿真与分析

5.1.1 单时间尺度FFRLS-AEKF联合估计

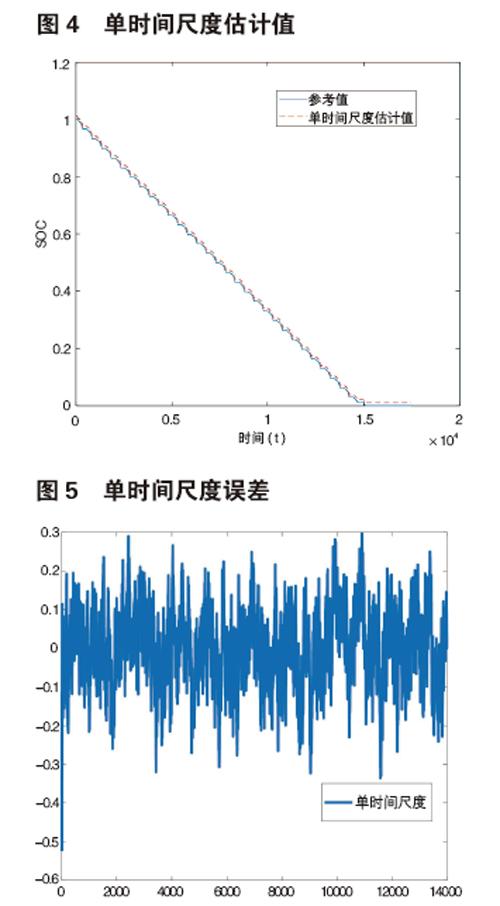
将模型参数辨识尺度和SOC估算时间尺度设为同一时间尺度L，L为1s的估计结果如图所示

图4所示为DST测试工况下单时间尺度FFRLS-AEKF算法的SOC估计值与SOC真实参考值曲线，图5为其误差曲线。

5.1.2 多时间尺度FFRLS-AEKF联合估计

将模型参数辨识尺度L从1s至30s逐渐增大，选取时间尺度L=5s，10s，20s，30s下的SOC结果表示不同时间尺度下的SOC估计结果。可得到不同时间尺度下SOC误差与估算消耗时间如图6所示：

从图中可以看出，不同时间尺度下SOC的精度是呈现非线性变化的，时间尺度在5s以内，SOC的误差几乎呈线性增长，但随着参数辨识时间尺度的增大（L>5），SOC误差有所下降，时间尺度增大代表电池在这段时间内的参数是不变的，相比较小时间尺度（L<5），参数是稳定的但是估算精度下降，这意味着在同一硬件单元中，可以减少处理器的运算时间，当时间尺度（L<5）时，计算消耗时间随时间尺度呈指数增长，当时间尺度（L>5）时，计算消耗时间随时间尺度增大下降不明显，此时的误差也较大。因此，综合计算成本和估算精度，最佳的时间尺度应选取在误差线和时间消耗线的交点处（L=2.5）。这时候的误差在可接受范围内，计算量也大幅减少。当L=2.5时，DST工况下SOC估计值、SOC真实参考值曲线及其误差曲线如图7、8所示。

由图7、8可见，当选取合适的时间尺度（L=2.5）时，算法的预测值能够很好的跟随参考值，误差在4%以内，不仅保证了估算的稳定性和精度，还节约了计算成本。因此，相比之下，多时间尺度FFRLS-AEKF对电池动态特性跟踪效果比单时间尺度更好。

6 结论

由于工作状态变化和老化会导致电池内部参数发生改变，本文利用FFRLS算法实时辨识电池模型参数，并在DST工况下验证了辨识方法。针对SOC算法在硬件处理单元中计算量大，消耗资源多问题，提出使用多时间尺度FFRLS-AEKF算法联合估计SOC，研究了不同辨识时间尺度对SOC估算的影响，结果显示，随着辨识尺度的增大，SOC估算精度也会随之下降，计算时间减少;在权衡考虑估算精度和计算消耗时间的条件下，时间尺度选取为2.5s可以既保证SOC的估算精度同时减少硬件的计算量，更加有利于SOC的估算。

基金项目：动力电池热管理及成组一体化关键技术开发  项目编号：BE2017008-1，BE2017008-4

参考文献：

[1]彭湃，程汉湘，陈杏灿，等.基于自适应卡尔曼滤波的锂电池SOC估计[J]. 电源技术，2017（11）：1541-1544.

[2]于海波，李贺龙，卢扬，等.基于混合卡尔曼滤波和H∞滤波的动力电池SOC估计[J].电力电子技术，2018，52（12）：63-66.

[3]印学浩，宋宇晨，刘旺，等.基于多时间尺度的锂离子电池状态联合估计[J]. 仪器仪表学报，2018，039（008）：118-126.

[4]魏克新，陈峭岩. 基于自适应无迹卡尔曼滤波算法的锂离子动力电池状态估计[J]. 中国电机工程学报，2014，000（003）：445-452.

[5]唐帅帅，高迪驹. 基于自适应卡尔曼滤波的磷酸铁锂电池荷电状态估计研究[J]. 电子测量技术，2018，041（014）：1-5.