核心素养下初中生几何推理能力的培养策略
2020-03-02孙向军
孙向军
(江苏省靖江市第三中学 214500)
一、探究分解图形,演绎论证推理
核心素养是思维品质、情感态度、关键能力的综合体现,学生在严谨的数学活动中,通过对数学概念本质的运算分析、理解欣赏、应用创新,逐渐形成良好的几何直观、推理能力和空间想象等素养能力.
例如,两张矩形纸片如下图方式进行放置,一张纸片的顶点在另一张的一条边上,要求学生解出1+2等于多少度?参考下图,学生可以利用平行线的性质定理进行解题,通过观察图形可以做辅助线构造内错角,求出正确结果.
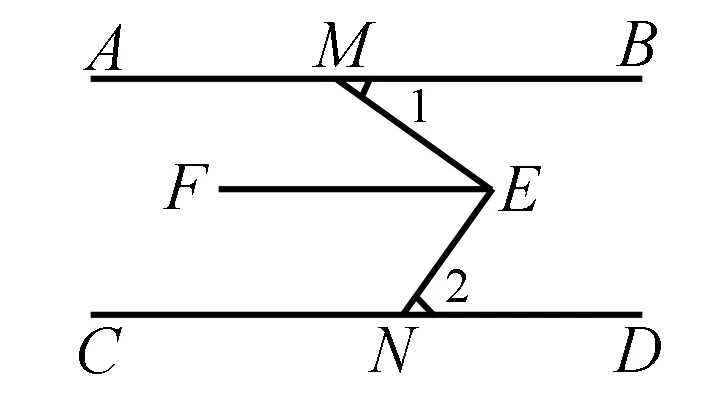
学生如图所示作辅助线构造内错角过E作EF∥AB,∵EF∥AB,∴∠1=MEF.∵AB∥CD,∵EF∥AB,∴EF∥CD,∴∠2=∠NEF.∵∠MEF+∠NEF=∠MEN=90°,∴∠1+∠2=90°.利用平行线的性质定理求解正确结果.
在梳理几何推理解题思路时,教师要为学生提供充足的时间观察识别图形,引导学生将题目中符号语言、文字、图形进行有效融合,深入思考分析“图形位置关系”并在图中进行标注,对需要作辅助线的位置作好辅助线,让学生边阅读题目边结合图形利用几何直观分析问题,在获取解题思路的过程中,有效加推理过程的严谨性,强化自身的联想思维与逻辑能力.
二、联想交流讨论,类比归纳推理
初中阶段学生处于逻辑思维和推理能力发展的关键时期,教师要突出学生的主体作用和价值,启发引导学生从个别事物所具备的本质属性出发,鼓励学生通过类比对象相似属性的归纳分析,推导出正确结论,促使学生在自主类比、猜想、观察、探究解题过程中建构新的知识概念.由于学生个体思维水平和认知领域有一定的局限性,教师在数学课程中要给予学生更多交流机会,促使学生在反复推理、分析、交流、思考的过程中发散思维,拓展解题思路,快速发现数学知识间的内在联系和共有性质.
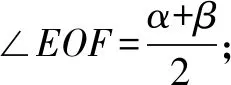
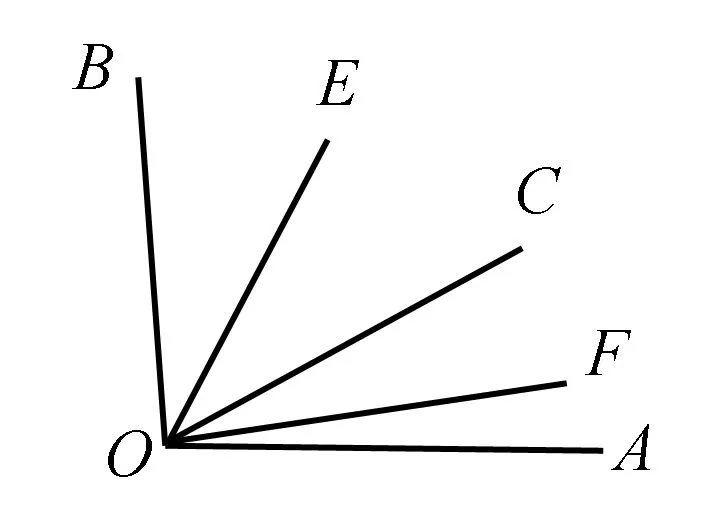
三、几何表达转换,自然描述推理
教师在数学核心素养理念下培养学生几何推理能力,应加强学生对几何相关概念、性质的理解和掌握,引导学生利用几何语言对相关问题进行描述性的论证和推理,使学生在推导解题过程中,灵活运用抽象思维和几何语言表达能力,从假设前提角度出发,在深刻掌握几何相关概念、性质的基础上,结合图形来观察、分析和解决问题.由于数学几何是高度抽象的概念性质,教师必须要有意识地引导学生理解、记忆、感受、体验几何概念的表达方式,让学生深刻掌握规范的几何语言以及各种基础知识,为了进一步提高教学效益让学生清晰体会几何表达方式,教师要学生们多感受、体验几何相关概念性质,让学生可以更好地理解几何语言,促使学生能在几何推理过程中,能将定理用规范的图形、符号、文字表达出来,并综合运用空间想象思维、数据分析能力、运算推理能力,来精准清晰地推理、解释几何概念.
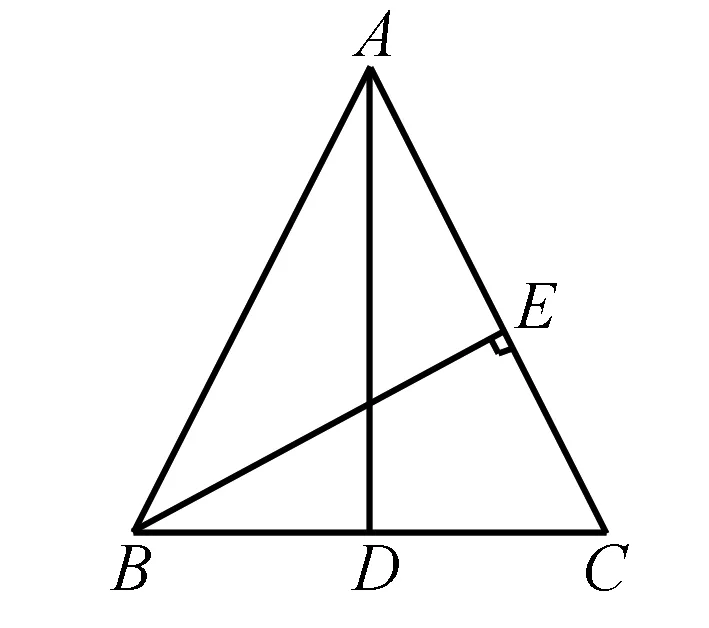
例如,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.要求学生求证:∠CBE=∠BAD.
解题过程中学生可联系“等腰三角形三线合一的性质”“角的等量代换”对几何问题进行推导.∵在△ABC中,AB=AC(已知),∴△ABC是等腰三角形,∠ABC=∠C.又∵△AD是BC边上的中线,△ABC是等腰三角形,∴AD⊥BC(三线合一),∴∠BAD+∠ABC=90°.又∵BE⊥AC(已知),∴∠CBE+∠C=90°.又∵∠ABC=∠C,∴∠CBE=∠BAD(等量代换).
在推理过程中教师要指导学生规范解题格式,使学生能在深刻理解和掌握几何相关概念、性质、定理基础上,运用几何语言对问题进行严谨表达、推导,进一步使学生的逻辑思维和推理分析能力得到有效的强化发展.
综上所述,教师在数学核心素养内涵背景下,发展和培养学生的几何推理能力,不仅可以强化学生数学逻辑思维,提高几何问题解题效率,还能有效激发学生的创新应用意识和空间想象能力.因此,教师在数学课程中,要引导学生感受和体验抽象的几何语言,发现知识之间的内在联系,使学生在解决问题时能巧妙结合几何图形、几何符号、文字信息,获取清晰直观的解题思路,促使学生在积极主动的观察、联想、探究、归纳过程中,深刻理解并掌握几何概念性质.
