浅析开放性数学问题的设计

陈 玺

(甘肃省陇南市成县城关中学 742500)

开放性数学问题的出现以及在近二十年来迅速普及，已被人们认为是最富有教育价值的一种数学题型.开放性数学问题的教学能真正地达到“教学是师生经验的展现与交流对话；教师是学生学习的合作者、促进者、组织者及引导者”，本能地体现师生互动.同时，教学还能给学生更多自主思考的空间，让学生多一份感悟，多一份理解，并提供更多的创新、发现新知识的机会.

开放性数学问题是相对于传统的封闭问题而言的，是指构成问题的背境材料、结论、解题依据和解题方法四个要素中缺少某些要素的命题.若缺少的要素是假设，则为条件型开放题；若缺少的要素是判断，则为结论型开放题；若缺少的要素是推理或解法等，则为策略型开放题.有的问题只给出一定的情境，其条件、解题策略与结论都要求主体在情境中自行设定与寻找，多方面、多角度、多层次地探索，则称为综合型开放题.

例1为使下列各式可以因式分解(在整数范围内)，a，p分别可以取哪些整数?

(1)x2+ax-18;(2)x2+7x+p.

分析第(1)小题中a的确定与-18的因数有关．

-18=1×(-18)=(-1)×18 =2×(-9)=(-2)×9 =3×(-6)=(-3)×6.

得到a可以取6种不同的数值，即±17，土7，±3．

第(2)小题中p的确定与7是哪两个整数的和有关．

7=3+4=2+5=1+6=0+7=(-1)+8=(-2)+9=(-3)+10=…， 所以p可以取无穷多个整数值，如12，10，6，0，-8，-18，-30等等.

由上例可知，在讲十字相乘法(新教材已删除)时可归纳：

(1)p是已知整数，对x2+ax+p进行分解时，因p的质因数有限，故a也有限；(2)a是已知整数，对x2+ax+p进行分解时，因a表示为两个整数的和的方法数是无穷的，故p也是无穷的.

仿照此类型，可设计出很多开放问题，旨在培养学生思维的灵活性和深刻性.

例2如图，在圆内接四边形ABCD中，AC=BD,AC、BD相交于P，根据这些条件，你能得出哪些结论?

解根据在同圆中等弧、等弦及圆内接四边形的有关性质及三角形全等或相似等性质，立即可得：

(1)弧AC=弧BD,弧AD=弧BC;(2)△APD≌△BPC;(3)DC∥AB，△PCD∽△PAB;(4)四边形ABCD是等腰梯形;(5)∠ADC+∠ABC=180°,∠DCB+∠DAB=180°.

例3今有一正方形土地，要在其上修筑两条笔直的道路，并把这块土地分成形状相同且面积相等的四部分.若道路的宽度忽略不计，请设计三种不同的修筑方案．(山东省中考题)

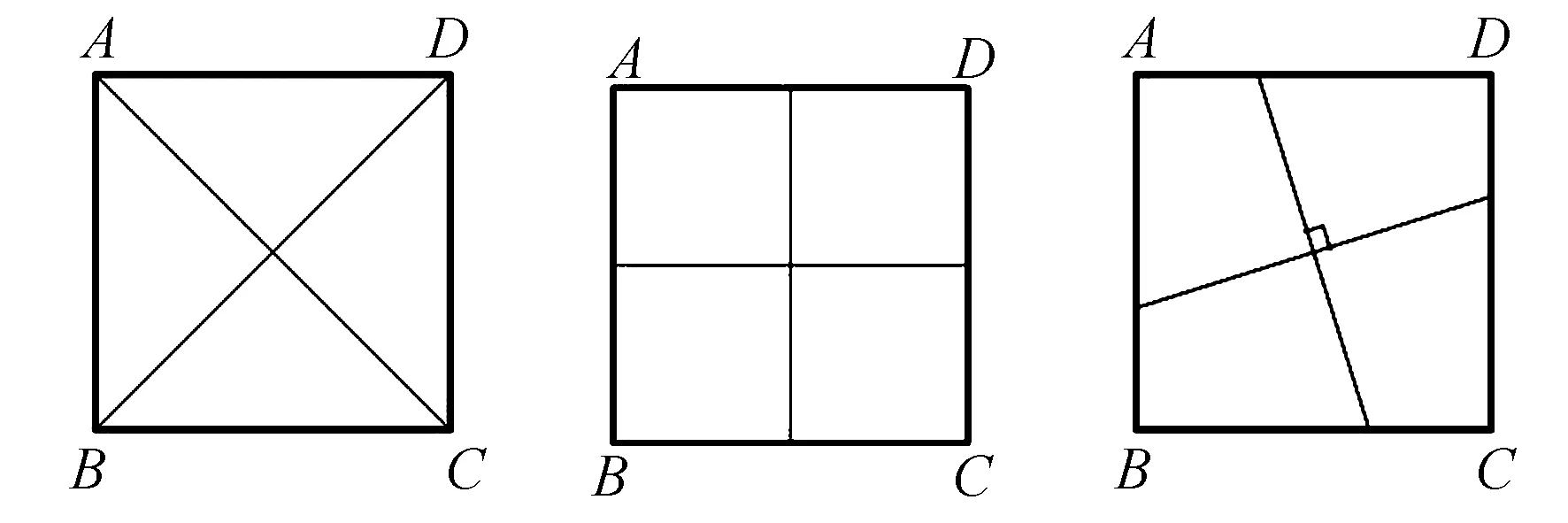
解(1)连结两条对角线；(2)连结两组对边中点；(3)过正方形对称中心任意作两条互相垂直的直线．

分析这是一道策略开放题，(1)、(2)最易想到，(3)是创新画法，显然(1)、(2)是(3)的特殊情况.

如将本题“大小相等”去掉，设计的方案是极多的．

例4如图，当△ABC≌△ADC时，显然有∠BAC=∠DAC,AB=AD,BC=DC.

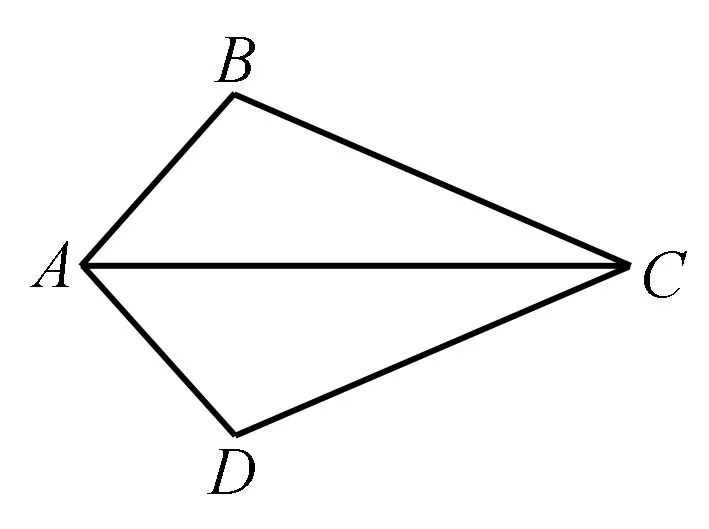
问题设计：在△ABC和△ADC中，有下列三个论断：

①AB=AD；②∠BAC=∠DAC；③BC=DC．

以其中两个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题：____.(陕西西安市中考题)

分析此题基本上是将例4中的条件与结论对调，进行设计的条件及结论均开放的题目，要求具有较高的分析能力.

三个论断中任何两个都可以作为条件，剩余一个论断则是结论，显然，可构造出3个命题：①、②⟹③；②、③⟹①；①、③⟹②．

其中2个是正确的，1个是错误的.考虑到“SSA”不能判定全等，故正确的命题是①、②⟹③或①、③⟹②．

由以上可看出，开放性数学问题的设计，必须在严格的逻辑性前提下，或是将原题条件抽象化，变通相应字母或项；或是在原题设上进行引伸；或是在原题结论上拓广；或是将题设部分与结论互调等等.既要对开放性问题进行“开放度”的把握和引导，又要对封闭题进行改造，让它适度开放.“开放”多少，“开放”多深，还要看学生的知识基础思维能力以及教材的内容等.

因此，教师在数学教学过程中，精心设计，合理、恰当地引进开放式教学，能充分体现学生的主体地位，学生的思维被全面激活，学生的概括能力和迁移能力得到提高，更好地反映学生的高层次思维，从而更有效地培养学生的逻辑思维能力和创新思维能力.同时，开放性数学问题的设计对教师的业务能力、 综合素质也是一个极大的挑战.