钢筋混凝土女儿墙对框架结构自振周期影响研究

2020-03-02王勇

铁道建筑技术 2020年12期

王勇

(中国铁建投资集团有限公司北京 100855)

1 引言

女儿墙是建筑外墙高出屋面的部分，在建筑结构中可以起到维护安全、防水收头、美化立面等作用。同时屋面女儿墙也是重要的建筑构件，与砌体结构的女儿墙相比，钢筋混凝土女儿墙提高了墙体抵抗水平荷载的能力。但是当女儿墙高度较大时，对结构的刚度会产生很大的影响，从而影响整体结构的抗震设计[1]。在框架结构的基本设计方法中，女儿墙通常被认为是非结构构件，不参与主体结构的受力分析，仅对其进行荷载统计和自身的抗弯验算[2]。白立新[3]提出将女儿墙的自重折算为线荷载作用到主体结构的设计方法。女儿墙作为建筑物檐头构造的一种形式，在地震作用中是一个薄弱环节。冯皓[4]对高度不超过1 000 mm的女儿墙抗震设计方法进行评估，指出当采用振型分解法时，突出屋面部分可作为一个质点；当采用底部剪力法时，要乘以增大系数3，并且增大部分不应再向下传递。杨秀瑞等[5]指出女儿墙在地震中的破坏虽然不会引起整个结构的破坏，但其倒塌极易造成人员伤亡，因此女儿墙的抗震锚固措施应引起足够的重视，并给出高度为600 mm女儿墙的一系列抗震锚固措施。目前针对高度较大的钢筋混凝土女儿墙对结构抗震性能影响的研究较少。

钢筋混凝土女儿墙对结构自振周期的影响主要来自两个方面:一方面女儿墙与顶层框架梁整体浇筑大幅提高了顶层框架梁的刚度，同时也提高了结构的整体抗侧刚度，可以减小结构的自振周期；另一方面女儿墙也是质量集中点，会增大结构的自振周期。规范[6]指出当采用底部剪力法分析女儿墙地震作用效应时，应考虑增大系数，但增大部分不再向下传递，只计入与该突出部分相连的构件。对嵌入抗侧力构件平面内的刚性建筑非结构构件，可采用周期调整法来考虑其刚度的影响。同时钢筋混凝土女儿墙与主体结构的框架梁等构件相连，会与其形成了深梁，增大了屋面梁的抗弯刚度，影响了主体结构的自振周期，对结构地震影响系数的取用产生影响，进一步影响了结构地震力的计算和最终配筋。因此，研究女儿墙对顶层框架梁刚度的影响以及女儿墙对整体框架结构自振周期的影响很有必要。

本文利用ANSYS软件，首先建立局部模型，研究女儿墙对与其相连的顶层框架梁刚度的影响；然后对整体框架结构进行有限元分析，得出女儿墙高度对结构自振周期的影响规律。

2 女儿墙对顶层框架梁刚度的影响分析

2.1 模型验证

规范[6]建议在结构内力和位移计算中中梁的刚度增大系数取2，边梁的刚度增大系数取1.5。为此，本研究利用ANSYS[7]软件建立独立矩形截面梁和“L”形、“T”形截面梁的有限元模型，得出其各自的刚度，并与给出的刚度放大系数进行对比，来验证所建立模型的可行性。

梁模型采用solid65单元。Amelia[8]提出可按照素混凝土构件截面刚度来计算构件的刚度，不讨论配筋率的影响，只考虑其在弹性阶段的力学性能。模型材料属性按照C30混凝土的材料标准来定义[9]。矩形截面梁和“L”形、“T”形截面梁的矩形部分宽度为250 mm，翼缘外伸长度为4 000 mm，梁跨度为8 000 mm。为研究不同梁高和板厚的比例对该刚度增大系数产生的影响，设定了3组不同的梁高和板厚，分别为600/100、650/130、600/150，梁高与板厚之比分别为 6∶1、5∶1、4∶1，而梁宽不变。沿梁的长度方向设置线荷载为10 kN/m[10]，对梁端均施加固定约束。为便于进行刚度对比分析，将矩形截面梁的刚度值设为1，见表1。网格划分及变形结果见图1～图2。

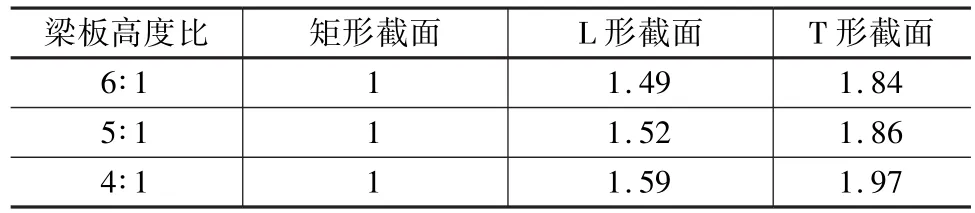
表1 考虑翼缘板作用时梁刚度增大系数

图1 框架梁网格划分

图2 框架梁变形云图

通过刚度对比分析可以看出，对于单侧翼缘，增大系数的数值在1.49～1.59之间，接近于规范的建议值1.5；对于双侧翼缘，增大系数的数值在1.84～1.97之间，略小于规范建议值2。通过比较刚度增大系数，验证了本研究中所采用的模型能够反映出框架结构的基本力学性能。

2.2 带有女儿墙顶层框架梁刚度分析

顾祥林等[11]指出钢筋混凝土梁构件开裂后刚度减小，并且减小程度受到配筋率的影响。当需要满足抗震设计要求时，计算中梁纵筋按贯通考虑，箍筋按非加密区箍筋考虑，并将其计入梁侧抗扭钢筋的影响[12]。本研究中通过改变女儿墙高与框架梁高之比，得出女儿墙高度对框架整体刚度影响，模拟结果见图3。在考虑了配筋率的影响之后，当女儿墙高度与框架梁高度之比为3时，复合构件的刚度与原框架梁－楼板刚度之比为4.26。复合构件变形图见图4。

图3 女儿墙对顶层框架梁刚度的增大效果

图4 带有女儿墙顶层框架梁变形云图

3 女儿墙对框架结构抗震性能的影响分析

本研究对照一个实际工程案例，利用ANSYS软件建立对应的结构模型，分析其动力特性和自振周期，从而考察女儿墙对框架结构抗震性能的影响。

3.1 有限元模型建立

整体框架结构模型平面布置见图5，立面布置见图6。柱截面类型有两种，中柱D-KZ-1，截面尺寸为800×700 mm；角柱 D-KZ-2，截面尺寸为 800×700 mm。基础顶面标高为－1.300 m，作为柱底嵌固部位，柱顶标高22.45 m。第一、二、三层横向主梁D-2KL2截面尺寸为350×900 mm，纵向主梁D-2KL1截面尺寸为300×700 mm。女儿墙厚度为210 mm，高度为2 100 mm。所有构件均采用C30等级混凝土。在有限元模拟分析过程中，将次梁对结构刚度的贡献折算到楼板，使得楼板更加接近刚性楼板的假定。因此，在本研究中有限元模型均不再单独建立次梁模型，通过增加楼板的厚度，以体现次梁对楼板刚度的增加。共建立三种框架结构的有限元模型:是否考虑女儿墙、将女儿墙视为增加刚度的梁以及将女儿墙视为独立的墙单元。各模型的具体参数见表2。

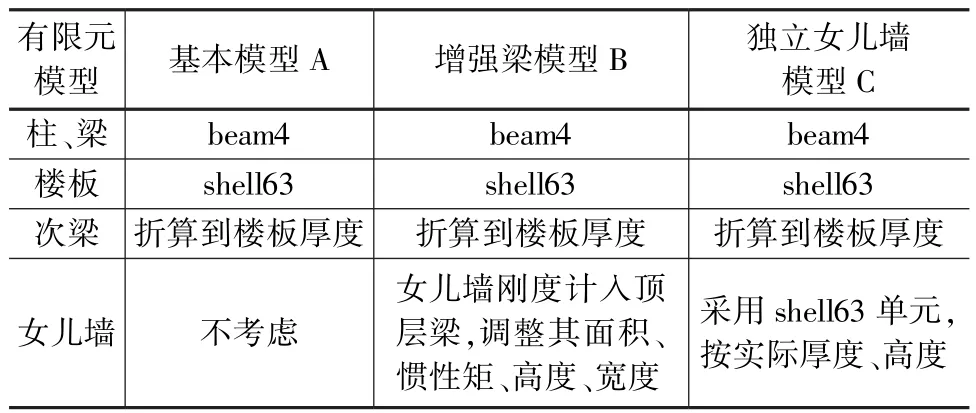
表2 结构整体刚度计算对比模型

图5 框架结构模型平面布置(单位：mm)

图6 框架结构模型立面布置(单位：mm)

在有限元模型中，梁、柱构件的主轴方向以及beam 4单元默认截面方向的y轴均平行于总体坐标系的x－y平面，对于不同方向的构件调整其θ角的数值。梁单元和楼板单元的网格划分需保证二者节点在模型中的位置保持一致。以模型C为例，结构局部和女儿墙的网格划分见图7。

图7 框架结构网格划分

三种模型中，将考虑女儿墙的模型A作为基本模型，与模型B和模型C形成对比。与模型B相比，模型C中女儿墙的布置方式更接近结构的实际布置，以下研究女儿墙对结构自振周期的影响时均采用模型C。

3.2 三种模型有限元模拟结果对比分析

分别对三种模型进行模态分析，通过分块兰索斯法进行模态提取，提取模态数目为4。表3列出了三种模型的模态分析结果及其自振周期(未考虑填充墙折减)。对比结果表明，模型B与模型C的周期非常接近，验证了模型C的可行性。图8对比了模型A与模型C得到的各阶振型周期，可以看出钢筋混凝土女儿墙对整体结构的前三阶振型的增大效果更加明显，对第四阶振型的影响较小。

表3 模型前四阶频率周期对比

图8 模型A与模型C各阶振型周期对比

3.3 女儿墙对框架结构自振周期影响分析

模型C前四阶振型见图9，其中一阶振型为短边方向的平动，二阶振型为长边方向的平动，三阶振型为扭转，四阶振型为弯扭。结构的第一、第二振型为平动，扭转周期出现在第三振型，说明结构在两个主轴方向的周期和振型相近，该结果符合规范要求。

图9 模型C前四阶振型

通过对比模拟结果得到的三种模型的自振周期，可以得出结论:对于基本结构和高度为2 100 mm的女儿墙，质量影响大于刚度的影响，因此结构的周期特别是第一振型的自振周期增大。

为研究女儿墙对结构自振周期的影响，改变女儿墙的高度，分别取300 mm、600 mm、900 mm、1 800 mm、2 100 mm。模拟结果表明女儿墙高度为600 mm时，自振周期的变化出现拐点，因此在女儿墙高度为300～900 mm之间按100 mm为增量再次改变女儿墙高度进行研究。当女儿墙高度在300～2 100 mm间变化时，与基本结构的第一振型至第四振型的周期和自振频率进行对比，见表4及图10。

表4 第一～第四振型周期及频率对比结果

图10 各阶振型周期对比

通过分析有限元模拟结果，女儿墙高度在600 mm附近时，对结构自振周期的影响最小，在第一、二、三阶振型这一结论更加明显。说明在刚度和质量影响结构自振周期的两个因素中，刚度的影响大于质量的影响，因此减小了结构的自振周期。当女儿墙高度在600 mm之外的范围时，质量的影响更加显著；当女儿墙高度为0～400 mm时，其对框架梁刚度的提高程度很小；当女儿墙高度为800～2 100 mm，女儿墙虽然使顶层框架梁和整体结构的刚度有所提高，但是质量对结构的影响更加明显，所以整体表现为结构的自振周期增大。第一阶振型中，当女儿墙高度在600 mm左右时，结构整体表现为自振周期减小，而当女儿墙高度为其他数值时，结构整体的自振周期均增大；达到第二阶振型时，无论女儿墙高度为任一数值，结构自振周期均增大，高度在600 mm时增量最小；达到第三振型时，女儿墙高度对结构自振周期的影响与第一阶振型相似；第四阶振型时结构的自振周期均小于基本结构。