双向近远场地震作用下大跨度钢桁拱桥易损性分析

刘 鸣

(中国铁建昆仑投资集团有限公司 四川成都 610000)

1 引言

远场地震与近场地震存在显著差异，近远场地震作用下土木工程结构的响应差异已经成了抗震研究的热点之一。近年来，钢桁拱桥因其施工简便和跨越能力强等特点逐渐成为铁路建设中跨越山谷、河道的典型结构[1]。部分钢桁拱桥常常包含多种类型构件，而近远场地震对不同类型构件造成的损伤可能存在较大差异，因此需要深入探讨。在此背景下，众多学者针对大跨度钢桁拱桥的抗震特性进行了广泛研究，如陈丽君[2]采用反应谱法和时程分析法计算了一座大跨度上承式钢桁拱桥在罕遇地震下的响应，对比了两种方法的计算结果并得到桥梁大震不坏的结论；赵灿晖[3]针对上承式钢桁拱桥采用时程分析方法得到了结构在不同维度地震荷载作用下的内力响应。尽管上述研究在钢拱桥的地震响应特性、减震措施等方面都取得了较大进展，但是其激励往往仅设置为1～3条地震；针对大跨度钢桁拱桥的易损性分析较少，特别是在近远场地震荷载对于易损性的影响以及桥梁多类型构件的易损性差异方面；仅考虑单维地震荷载作用，关于双向地震荷载作用下桥梁结构易损性情况尚不明确。

针对上述问题，本文基于概率性地震需求分析(PSDA)方法，分析大跨度上承式钢桁拱桥在双向、近远场地震作用下的易损性。借助OpenSEES开源平台建立全桥模型；选择适用于双向地震损伤评价的应变指标进行损伤评估；全面考虑地震、损伤指标与桥梁结构本身的不确定性，通过增量动力分析方法(IDA)生成地震样本，利用LHS抽样法获得桥梁样本；得到纵、横以及双向地震作用下桥梁关键构件的损伤程度，以峰值加速度(PGA)作为地震强度参数绘制易损性曲线，对比分析桥梁在双向、近远场地震作用下的损伤概率。

2 桥梁模型构建

本文对一座大跨度铁路上承式钢桁拱桥进行研究。桥梁跨度为490 m，主梁为梁高3 m的钢箱梁，桥面宽度为24.9 m，孔跨布置为14×37.2 m；拱上墩采用钢箱截面刚架墩；主拱圈为矢高109.5 m的提篮式钢桁拱，拱肋截面为边长2 m的矩形四片桁；交界墩为钢筋混凝土刚架墩。

借助OpenSEES平台建立桥梁弹塑性模型。全桥构件由dispBeamColumn单元模拟，并划分纤维截面。几何非线性通过设置局部坐标实现。材料非线性通过设置非线性本构实现，钢材采用双线性模型steel02模拟；混凝土采用经Scott修正的Kent-Park模型concrete02模拟；交界墩混凝土本构参考文献[4]，拱脚混凝土采用Mander模型本构[5]；支座采用zeroLength单元模拟，边界条件为全固结。全桥施加3%的瑞利阻尼。全桥模型见图1。通过特征值分析，主要振型见图2。

图1 全桥模型

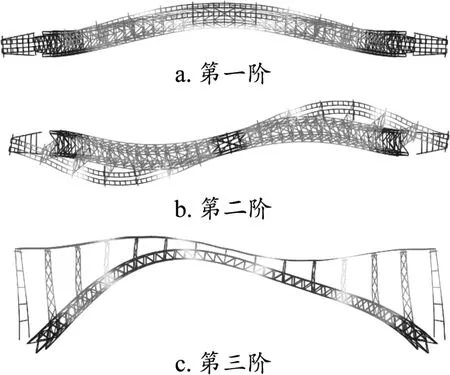
图2 主要振型

3 易损性分析方法

3.1 概率性地震需求分析方法

通过非线性时程分析获得桥梁地震响应(地震需求Y)，Y的对数中位数与地震强度(X)的对数中位数服从线性关系[6]，见式(1)。X与Y符合对数正态分布，构件超过特定损伤指标(Z)的失效概率可以通过标准正态分布函数φ表示，见式(2)。将式(1)代入式(2)，可以得到以X为自变量的易损性公式，见式(3)。

式中，y、x、z分别为Y、X、Z的中位数；a和b为常数；分别为Y和Z的对数标准差。

3.2 地震强度与构件损伤指标

本文根据钟剑[7]对PGA、PGV、Sa等参数的对比研究，选择PGA作为地震强度参数。对于损伤指标的研究较多，主要分为单参数、双参数损伤指标两类。由于应变指标输出简单、概念清晰，并且适用于双向地震损伤评价，因此本文选择材料应变作为损伤指标，并将损伤分为基本完好、轻度损伤、中等损伤、严重损伤、倒塌五个等级。对于纯钢构件，以1、2、8.4倍的钢材屈服强度[8]作为划分依据；对于混凝土以第一极限状态的压应变限值、0.01、0.03、0.05作为划分依据[9]；对于钢管混凝土构件与钢筋混凝土构件的钢材以屈服强度、0.01、0.03、0.05作为划分依据。

3.3 易损性模型的不确定性

(1)地震样本的不确定性

通过收集大量地震记录实现地震样本的不确定性。本文选择10条近场地震[10]与10条远场地震[11]，将地震的PGA通过IDA方法进行调幅，从0.1 g以步长0.1 g调幅至1.5 g，生成300条地震，其加速度反应谱见图3。从图3可以看出，近场地震在周期1～2 s范围内仍然具有较高的幅值，大跨度桥梁由于具有较大的自振周期会导致更强烈的地震响应。

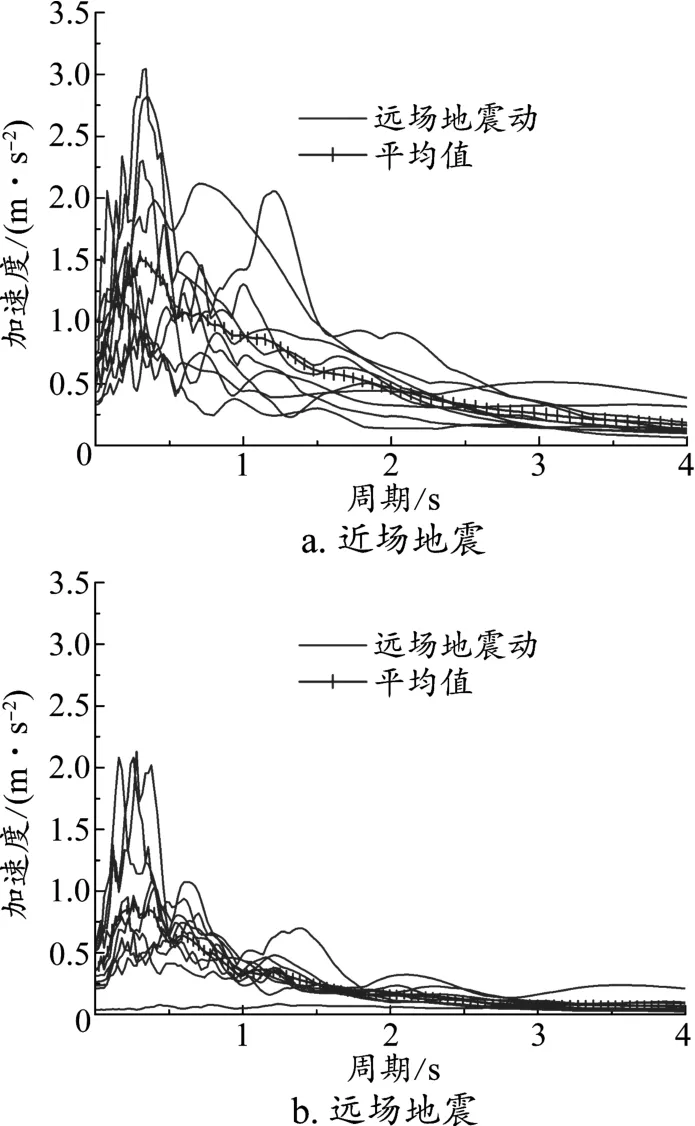
图3 地震加速度反应谱

(2)桥梁样本的不确定性

真实桥梁结构由于制造、安装、环境变化等因素具有一定的不确定性，这些不确定性对地震易损性分析的影响不可忽略。考虑混凝土抗压强度、钢材屈服强度与弹性模量的不确定性，采用LHS抽样方法[12]生成300个桥梁样本与300条地震一一对应。

(3)损伤指标的不确定性

由于材料存在离散性，导致材料的损伤指标也具有不确定性。通过统计300个桥梁样本的数据，得出钢材与混凝土损伤指标的中位数(z)与对数标准差(βz)。

4 桥梁易损性分析

对桥梁纵、横、双向(纵向＋横向)施加地震力，通过非线性时程分析，获得最大响应。选取损伤最严重的纯钢构件(跨中主梁与1/4拱肋)、钢管混凝土构件(拱脚)及钢筋混凝土构件(交界墩底部)进行分析。将其应变响应与PGA进行回归分析，求得a、b、βy、βz并根据式(3)得出构件的易损性曲线。

(1)纯钢构件

图4为纯钢构件在近远场地震作用下的构件易损性曲线。由图4可知，纯钢构件在不同方向输入地震时，纵向与双向结果较为一致，双向甚至略有减小，横向最小。可见输入垂直于主导方向的地震，有可能会减弱主导方向地震的影响。大跨度桥梁横向刚度较小，横向周期较长，与地震的卓越周期差距较大，因此地震横向输入下纯钢构件损伤概率基本为0。

图4 纯钢构件易损性曲线

对比纯钢构件在近远场地震作用下损伤概率，在PGA较小时差异很小，对于跨中主梁远场损伤甚至超过近场，随着PGA增大差异逐步增加。总体而言，纯钢构件轻微损伤概率最大为98%，发生中等及严重损伤可能性不大，展现出较好的抗震性。

(2)钢管混凝土构件

由图5可知，钢管混凝土构件在地震不同方向输入时，双向损伤概率最大，横向次之，纵向最小。双向地震输入能量较大，因此损伤概率最大，而横向结果大于纵向，说明拱脚对于横向地震作用更为敏感。对比钢管与混凝土的易损性，混凝土损伤概率远小于钢管，拱脚的损伤主要由钢管控制。可见对于钢管混凝土构件，主要由钢管通过变形承担大部分地震荷载，混凝土受钢管保护因此损伤概率较小。

图5 钢管混凝土构件易损性曲线

对比近远场地震作用结果，仍是近场地震造成的损伤概率大于远场，钢管与混凝土的结果差异都随着PGA增大不断增加，其中钢管的差异比混凝土更大。总而言之，拱脚的截面及材料设计较为保守，发生损伤可能性很低，最高的轻微损伤概率为82%，中等损伤基本不会发生。

(3)钢筋混凝土构件

由图6可知，钢筋在纵向和双向地震作用下的损伤概率基本一致，而混凝土损伤概率却显著增加。这表明地震能量较低时，钢筋可以通过自身的延性变形承担地震荷载，但是随着地震能量增大，混凝土参与到耗能中，由于材料的脆性会导致损伤快速发展并呈现非线性增长，因此会大大增加构件中等与严重损伤概率。

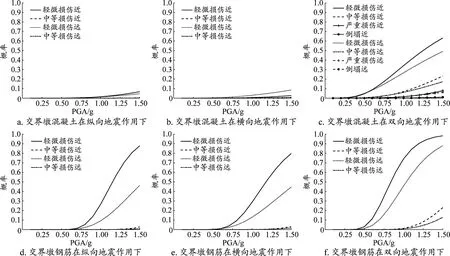
图6 钢筋混凝土构件易损性曲线

比较近远场地震作用，近场地震造成的损伤概率基本大于远场，不过在横向地震作用下混凝土会得出相反结果，可见近场地震造成的损伤不一定比远场大，对于桥梁不同构件进行近远场地震的分开讨论是必要的。混凝土随着PGA增大结果差异不断增加，且随着损伤等级加大差异减小。钢筋在PGA为1.4 g附近，纵向与横向地震损伤概率差异最大，为42%(纵向地震作用时)。总体而言，交界墩损伤概率比前述构件大，轻微损伤概率最高为98%，中等与严重损伤概率最高分别为23%和8%。

5 结论

基于概率性地震需求分析法对大跨度钢桁拱桥进行双向、近远场地震易损性分析，得到以下结论:

通过对比不同材料易损性差异发现，低能量地震时，钢材可以通过自身的良好延性变形承担地震荷载，但是随着地震能量增大，混凝土参与到耗能中，由于材料的脆性会导致损伤快速发展并呈现非线性增长，因此混凝土严重与中等损伤概率会超过钢材。

比较近远场地震作用，近场地震造成的损伤概率基本大于远场地震。在同一损伤等级时，差异随着PGA增加不断增大。在同一PGA时，差异随着损伤等级加大而减小。近远场地震对于不同构件与材料的损伤存在差异，构件中交界墩损伤差异最大为42%，材料上对钢材影响比混凝土大。

对于不同构件，1/4拱肋与跨中主梁轻微损伤概率最高为98%，中等、严重损伤概率不高，展现出较好的抗震性。拱脚由于拥有强壮的截面以及高强度的材料，发生损伤可能性很低，轻微损伤概率最高为83%，基本不会发生中等损伤。交界墩损伤可能性比前述构件高，轻微损伤概率最高为98%，中等与严重损伤概率最高分别为23%和8%。