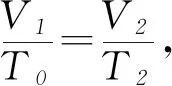热学图象问题及其求解策略
2020-02-29刘琨
刘 琨
热学图象问题在高考中经常出现,题型多样,但对该类问题的求解一直是考生的难点,问题多多.究其原因,多是考生没有搞清楚热学图象的物理意义,不明白图象中隐含的物理过程,导致失误连连.实际上,只要搞清楚以上两点,有关热学图象问题的求解还是比较容易的.
1 图象的物理意义
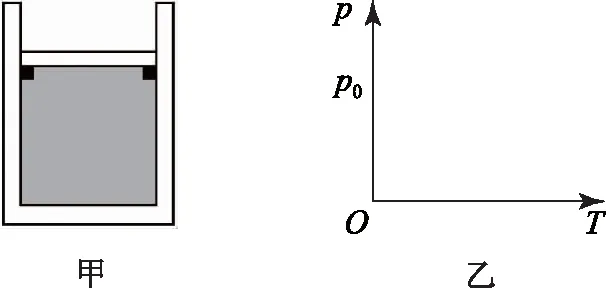
例1用DIS研究一定质量的气体在体积不变时压强与温度的关系,部分实验装置如图1-甲所示,研究对象为密闭在试管内的空气.实验得到如图1-乙所示的p-t图象,由图可知温度每升高1℃,压强增加________Pa;若改用体积较大的试管密封初始温度和压强均相同的气体再次实验,得到图线的斜率将________(填“增大”“减小”或“不变”).

图1
解析 本题解题关键是明确p-t图象的斜率的物理意义,结合查理定律列式分析得到斜率的表达式,进一步分析即可求解.
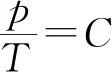
p-t图象的斜率为

2 图象的转换问题
我们知道,理想气体的状态参量涉及三个,即p、V、T,而所谓图象的转换问题,即是将其中两个参量的状态变化过程的图象转换为涉及第三个参量的图象,如将V-T图象转化为p-V图象,或者转化为p-T图象.此类问题的解决,必须建立在准确理解图象的物理意义的基础之上.
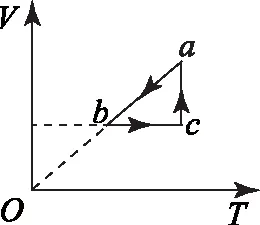
图2
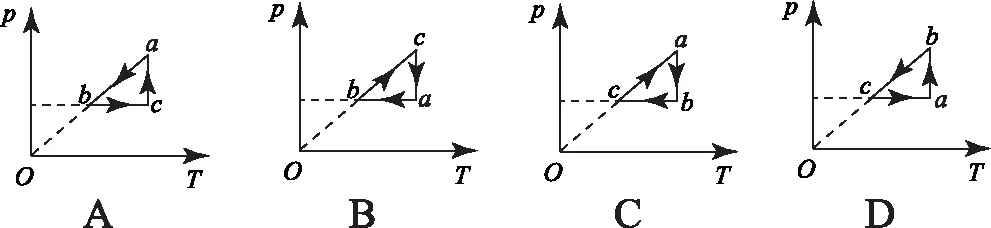
例2如图2为一定质量的理想气体的状态变化过程的V-T图象.则与之相对应的变化过程p-T图象应为下图中( ).
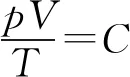
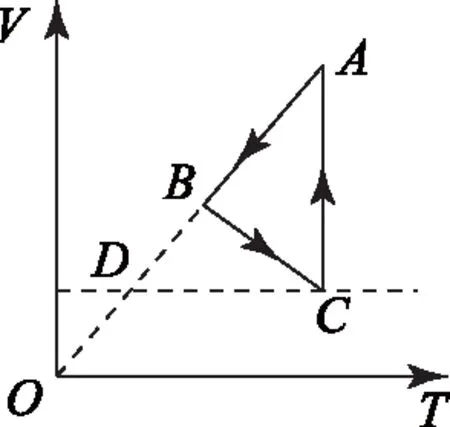
例3如图3所示,一定质量的理想气体从状态A经B、C、D再回到A,问AB、BC、CD、DA分别是什么过程?已知在状态A时体积为1 L,请把此图改画为p-V图象.
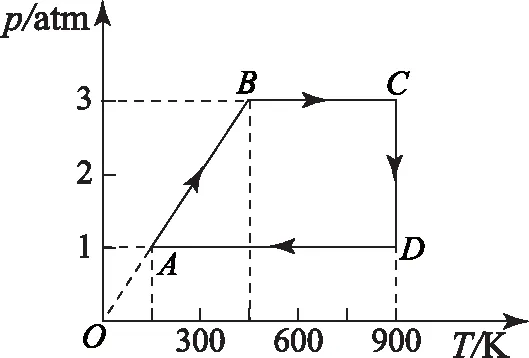
图3
解析AB过程是等容升温升压;BC过程是等压升温增容,即等压膨胀;CD过程是等温减压增容,即等温膨胀;DA过程是等压降温减容,即等压压缩.

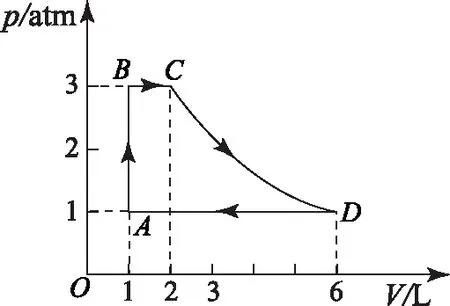
图4
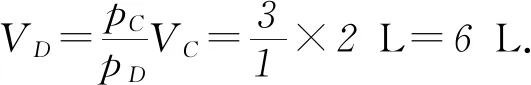
容易得到改画的p-V图象如图4所示.
3 不同状态下参量的比较
此类问题考查气体的状态方程中对应的图象,解答此类题目要能从图象中获取有用信息,判断出气体状态情况,特别要注意在p-T图象中等容线为过原点的直线.
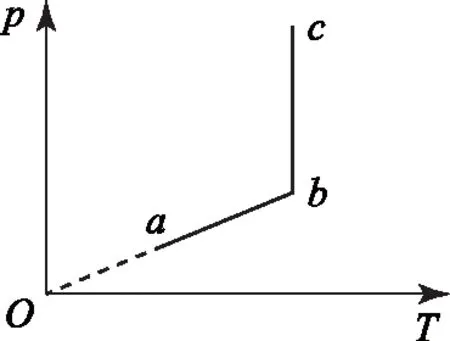
图5
例4一定质量的理想气体状态变化的p-T图象如图5所示,若用ρa、ρb、ρc和Va、Vb、Vc分别表示气体在a、b、c三种状态下的密度和体积,则( ).
A.ρa>ρb>ρc,Va>Vb>Vc
B.ρa=ρb<ρc,Va=Vb>Vc
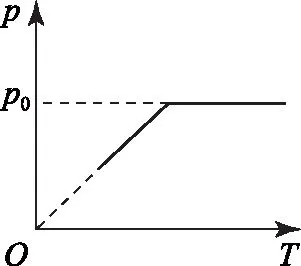
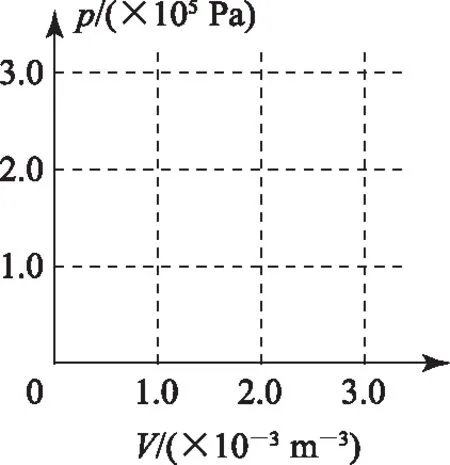
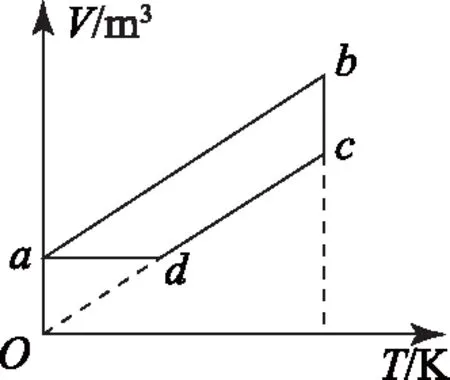
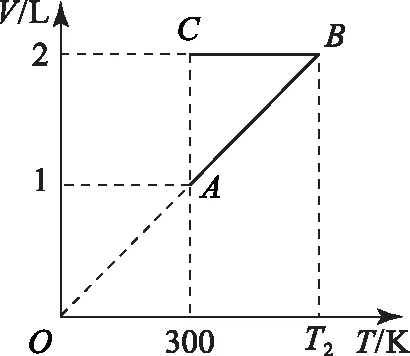
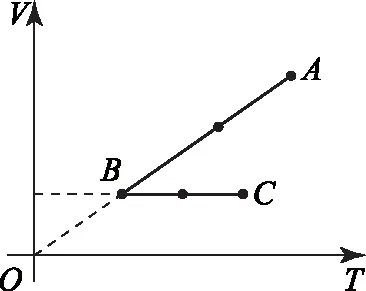
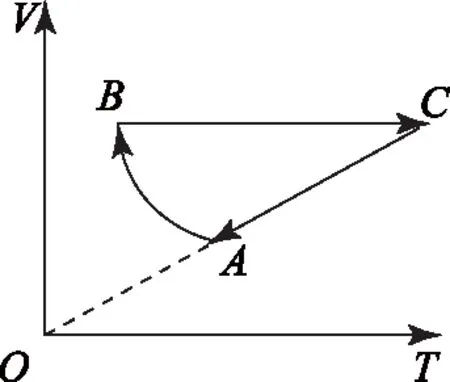
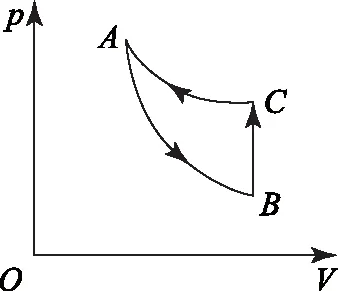
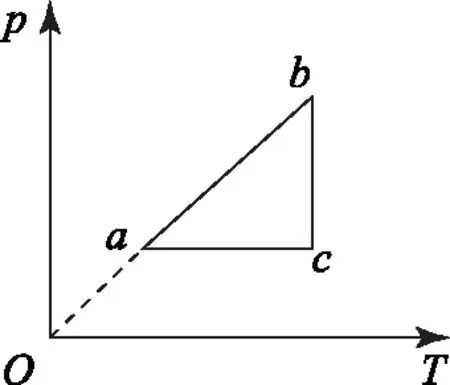
C.ρa=ρb>ρc,Va D.ρa<ρb<ρc,Va 图6 例5如图6所示,一定质量的理想气体,经过图线A→B→C→A的状态变化过程,AB的延长线过O点,CA与纵轴平行.由图线可知( ). A.A→B过程气体压强不变,密度减小 B.B→C过程气体压强增大,密度增大 C.B→C过程气体温度升高,密度减小 D.C→A过程气体温度不变,密度增大 图7 解析 由图示图象判断气体的状态变化过程,应用理想气体状态方程判断气体体积的变化,然后根据m=ρV判断密度的变化. 由图示可知,AB过程,气体体积与热力学温度成正比,则气体发生等压变化,气体压强不变,体积减小,密度变大,故选项A错误;如图7过C作做等容线,则体积相等的情况下,C的温度高,所以C的压强一定比AB的压强大,由图可知B→C过程气体体积减小,温度升高,故密度增加,选项B正确,选项C错误;而由于C的压强一定比A、B两点的压强大,所以C→A过程压强减小,由图可知C→A过程气体的体积增大,密度减小,故选项D错误. 图8 例6如图8是一定质量理想气体状态变化的V-T图象,图中ab∥cd,由图象可知( ). A.a→b过程气体压强不变 B.b→c过程气体内能不变 C.c→d过程气体密度不变 D.d→a过程气体对外做功 解析 本题主要考查对V-T图象的理解,要能通过V-T图象判断气体状态的变化.当气体体积增大时,气体对外做功,当气体体积减小时,外界对气体做功. 在V-T图象中,过坐标原点的直线为等压变化,ab不过坐标原点,故不是等压变化,选项A错误;由图8可知,bc为等温变化,温度不变,则内能不变,故选项B正确;c到d为等压变化,体积减小,由于质量不变,故密度增大,故选项C错误;d→a为等容变化,气体对外不做功,故选项D错误. 图9 例7封闭气缸内一定质量的理想气体由状态A经状态B再变化到状态C,其体积V随热力学温度T变化的关系图象如图9所示.若状态A变化到状态B的过程中气体吸收热量Q1=240 J,气体在A状态对应的压强为p0=1.0×105Pa.求: (1)气体在状态B时的温度T2; (2)气体由状态B变化到状态C的过程中,气体向外传递的热量Q2. (2)A到B过程由热力学第一定律得WAB+QAB=ΔUAB,即-p(VB-VA)+Q1=ΔUAB. B到C过程中,有WBC+QBC=ΔUBC,即有0-Q2=ΔUBC. 又TA=TC,所以 ΔUBC=-ΔUAB,得Q2=140 J,即B到C过程中,气体向外传递热量140 J. 图10 例8带有活塞的气缸内封闭一定量的理想气体,气体开始处于状态A,由过程AB到达状态B,后又经过程BC到达状态C,如图10所示.设气体在状态A时的压强、体积和温度分别为pA、VA和TA,在状态B时的体积为VB,在状态C时的温度为TC. (1) 求气体在状态B时的温度TB; (2) 求气体在状态A时的压强pA与状态C时的压强pC之比. 解析A→B过程为等压变化;B→C过程为等容变化. 理想气体实验定律和热力学第一定律作为热门考点,必须重点强化和训练.而热力学第一定律结合气体实验规律考查是高频考点,复习时应注意过程的选择,以及物理量符号的确定,规范书写,提高得分率. 图11 例9一定质量的理想气体经历了图11所示的A→B→C的状态变化过程,则( ). A.A→B过程中,压强不变 B.A→B过程中,外界对气体做负功 C.B→C过程中,气体分子间距增大 D.B→C过程中,气体分子无规则热运动变剧烈 E.C→A过程中,气体对外放热 图12 例10如图12所示,一定质量的理想气体,从状态A经绝热过程A→B、等容过程B→C、等温过程C→A又回到了状态A,则( ). A.A→B过程气体降温 B.B→C过程气体内能增加,可能外界对气体做了功 C.C→A过程气体吸热 D. 全部过程气体做功为零 图13 例11一定量的理想气体从状态a开始,经历三个过程ab、bc、ca回到原状态,其p-T图象如图13所示.下列判断正确的是( ). A. 过程ab中气体一定吸热 B. 过程bc中气体既不吸热也不放热 C. 过程ca中外界对气体所做的功等于气体所放的热 D.a、b和c三个状态中,状态a分子的平均动能最小 解析 过程ab,理想气体等容变化,温度升高,理想气体的内能增大,气体一定吸热,选项A正确;过程bc,体积变大,气体对外做功,气体一定吸热,选项B错误;过程ca,理想气体的压强不变,温度降低,内能减小,体积减小,外界对气体做功,气体对外放出的热量大于外界对气体做的功,选项C错误.根据上述三过程可知在a、b、c三个状态中,状态a的温度最低,根据温度是分子平均动能的标志,可判断其分子的平均动能最小,选项D正确.本题应该选A、D. 在高考试题中,近年还经常出现综合性的计算题,可能同时涉及上述多个问题,必须灵活运用相关知识求解. 例12如图14-甲所示,U形气缸固定在水平地面上,用重力不计,面积S=10 cm2的活塞封闭着一定质量的气体,已知气缸不漏气,活塞移动过程无摩擦.初始时,外界大气压强为p0=1.0×105Pa,活塞紧压小挡板.现缓慢升高缸内气体的温度. 图14 (1) 请在乙图中作出能反映气缸内气体的压强p随热力学温度T变化的图象; (2) 当温度缓慢升高到t1=27 ℃时,活塞与小挡板间恰好无作用力.现在活塞上加一质量为m=5 kg的砝码,要使加砝码后的活塞与小挡板间恰好无作用力,则温度至少要升高到多少摄氏度? 图15 解析 (1) 因开始时活塞紧压小挡板,说明被封闭气体的压强小于大气压,在活塞离开挡板之前,气体的体积不变,做等容变化,图线过p-T图象的坐标原点,活塞离开挡板后,做等压变化,由此可知气缸内气体的压强p随热力学温度T变化的图象如图15. (2)对气缸内气体 T1=300 K,p1=p0=1.0×105Pa, 图16 例13内壁光滑的导热气缸竖直浸放在盛有冰水混合物的水槽中,用不计质量的活塞封住压强为1.0×105Pa、体积为2.0×10-3m3的理想气体.现在活塞上方缓缓倒上沙子,使封闭气体的体积变为原来的一半,然后将气缸移出水槽,缓慢加热,使气体温度变为127℃. (1) 求气缸内气体的最终体积; (2) 在p-V图上画出整个过程中气缸内气体的状态变化.(大气压强为1.0×105Pa) 解析 气体开始做的是等温变化,后来做等压变化,由玻意耳定律与盖·吕萨克定律列方程,可以求出气体的最终体积,然后作出气体状态变化的p-V图象即可. 图17 (2)第一个过程是等温过程,由pV=C可知,p与V成反比,图象是反比例函数图象;第二个过程是等压过程,气体的压强不变,温度升高,体积变大,图象是一条平行于V轴的直线,整个物理过程的p-V图象如图17所示.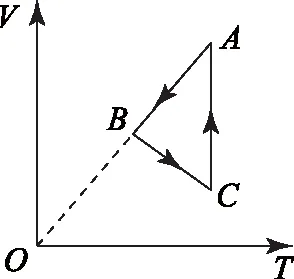
4 图象中有关参量的计算
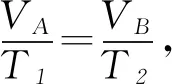
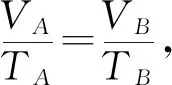
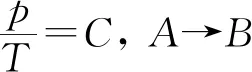
5 图象与热力学第一定律综合应用问题
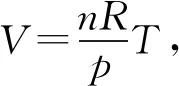
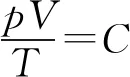
6 与图象有关的综合计算题