基于高阶累积量和DNN模型的井下信号识别方法

王安义， 李立

(西安科技大学 通信与信息工程学院， 陕西 西安 710054)

0 引言

近年来无线通信技术快速发展，带动了煤矿产业逐渐走向智能信息化。当前矿井下存在2G，3G，4G，WiFi等多种无线通信系统。由于不同的通信系统采用的信号调制方式不同，导致在矿井这种限定空间中，通信系统的可靠性、兼容性、智能性较差。准确识别信号调制方式从而进行信号解调是提高矿井通信系统可靠性和智能性的关键[1]，也是解决矿井信息网络异构问题的重要方法。

现有的信号调制识别方法中，基于判决理论的识别方法判决准则简单，理论成熟，但需要非常多的信号先验信息[2-3]；基于高阶累积量特征的算法能够在计算简便度和算法性能之间进行权衡，且抗噪能力良好，因而成为研究热点[4-7]；此外，深度学习算法也被应用到无线通信信号识别领域[8-11]。这些研究大多只考虑了比较理想的高斯白噪声信道，对井下复杂衰落信道环境下的信号识别问题研究较少。王艳芬等[12-13]对井下信道模型进行了深入研究，确定了井下Nakagami-m信道模型的参数值。本文在此基础上，给出了矿井Nakagami-m衰落信道环境下OFDM，BPSK，QPSK，8PSK，2FSK，4FSK，8FSK，32QAM，64QAM等9种数字信号的调制识别方法。该方法结合了高阶累积量特征和深度神经网络模型，增加了识别信号的种类，提高了矿井巷道环境下的信号识别率。

1 高阶累积量的特征分析及提取

1.1 高阶累积量理论

对接收到的含噪声数字调制信号进行下变频处理得到复基带信号sk：

(1)

式中：xk为发送信号，k=1,2,…,N，N为码元长度；nk为加性噪声；P为接收信号功率；θc为载波相位；ak为基带信号。

对于零均值的复随机过程x(t)，其v阶累积量和v阶混合矩分别为

Cvg=Cum[X1,X2,…，Xv]=

(2)

Mvg=E[x(t)v-gx*(t)g]

(3)

式中：Cum(·)表示求累积量；∑(·)表示在所有互不连通的有序分割合集X=(X1,X2,…,Xv)内求和；q为分割的子集数；E(·)为数学期望；Uj为q个子集当中第j个子集元素的下标集；x*(t)为x(t)的共轭；v为阶数；g为共轭个数。

联立式(2)和式(3)可得到累积量表达式：

(4)

各调制信号的高阶累积量理论值见表1。

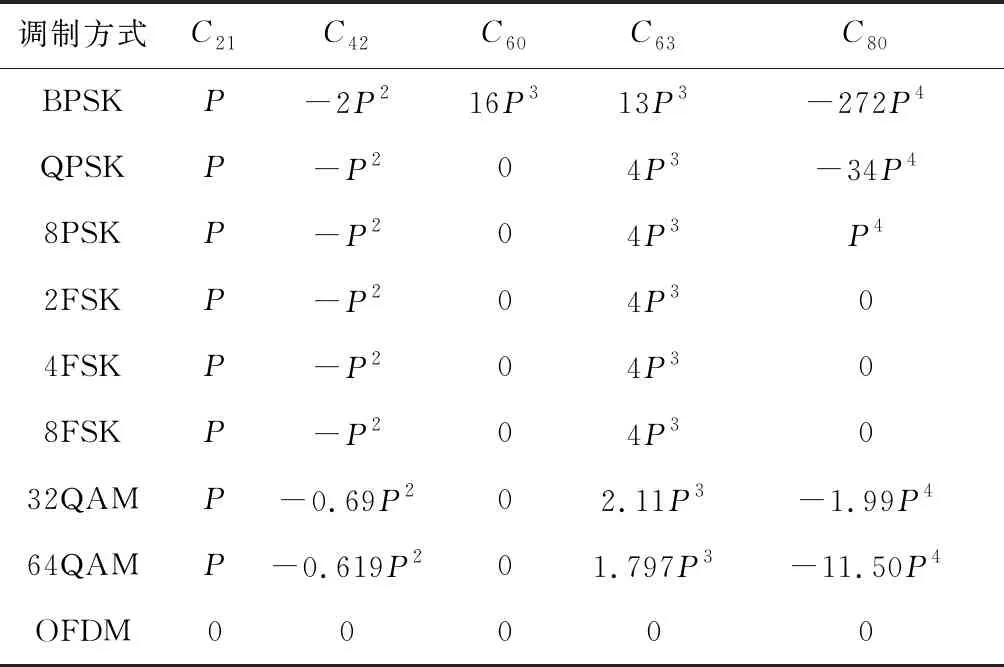
表1 各调制信号的高阶累积量理论值Table 1 High-order cumulants theoretical value of each modulation signal

由表1可知，MFSK的类内信号各阶累积量完全一样，无法直接利用累积量构造特征来实现信号识别。对此，通常情况下需要联合调制信号的其他特征参数来识别，如循环谱特征、瞬时特征参数等[6]。本文对接收信号进行预处理后将其分成2路，一路信号先进行傅里叶变换，再计算高阶累积量，另一路信号直接计算高阶累积量。与微分处理[7]的MFSK信号相比，经傅里叶变换后的MFSK信号高阶累积量特征有更加明显的辨识度。

1.2 特征参数提取的理论分析

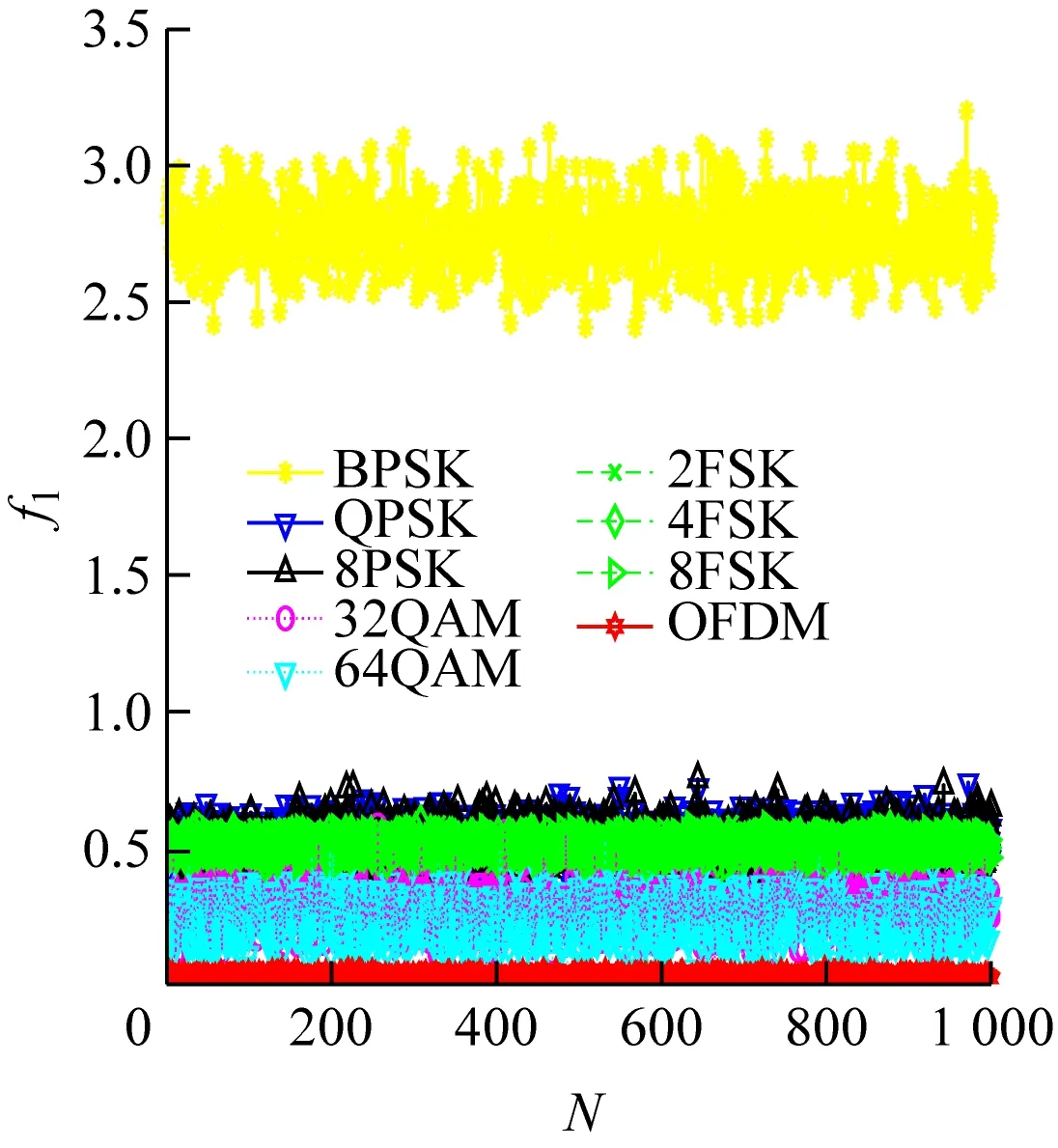
(a) 特征参数为f1,信噪比为0 dB

(b) 特征参数为f2,信噪比为0 dB

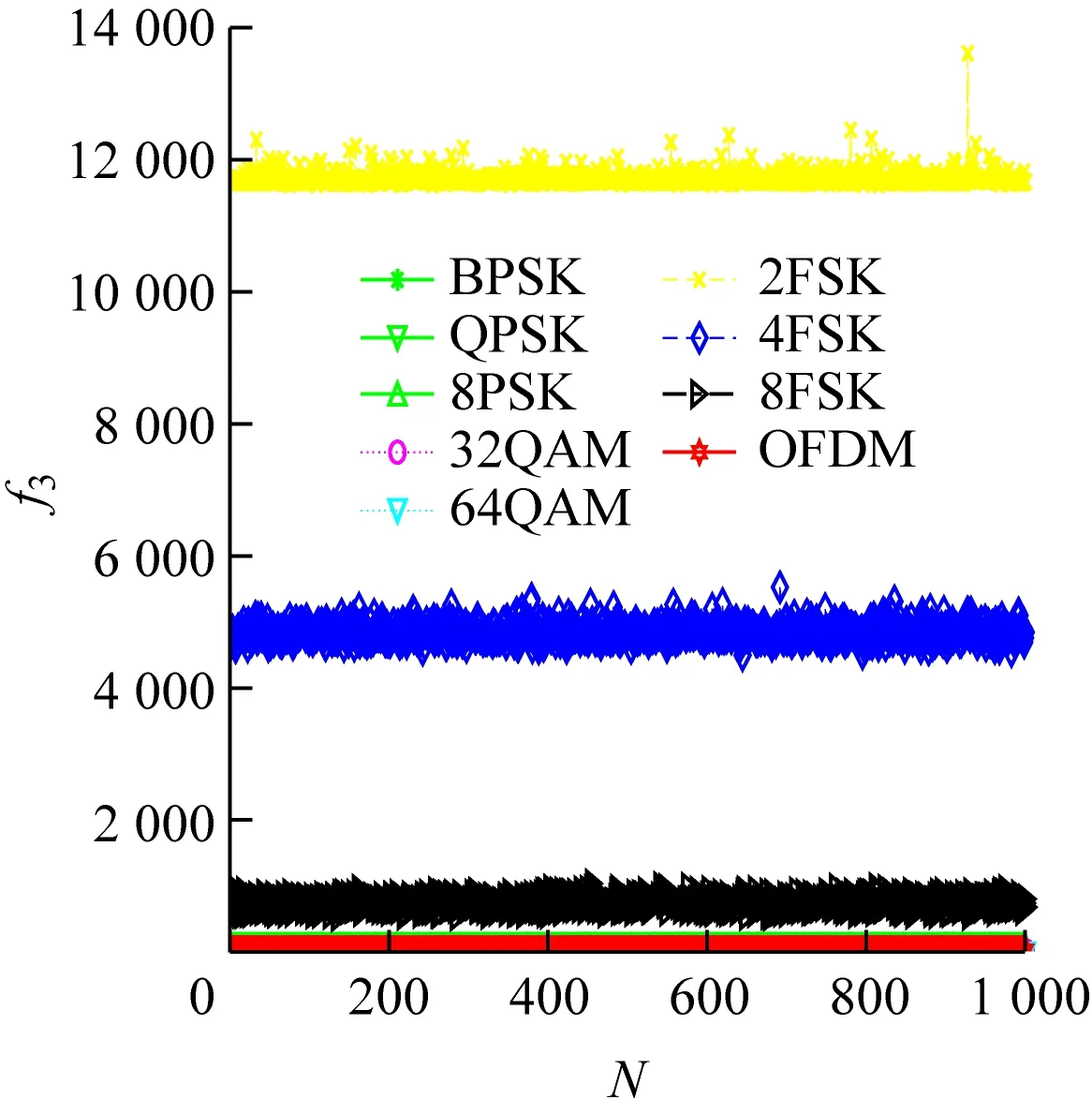
(c) 特征参数为f3,信噪比为0 dB

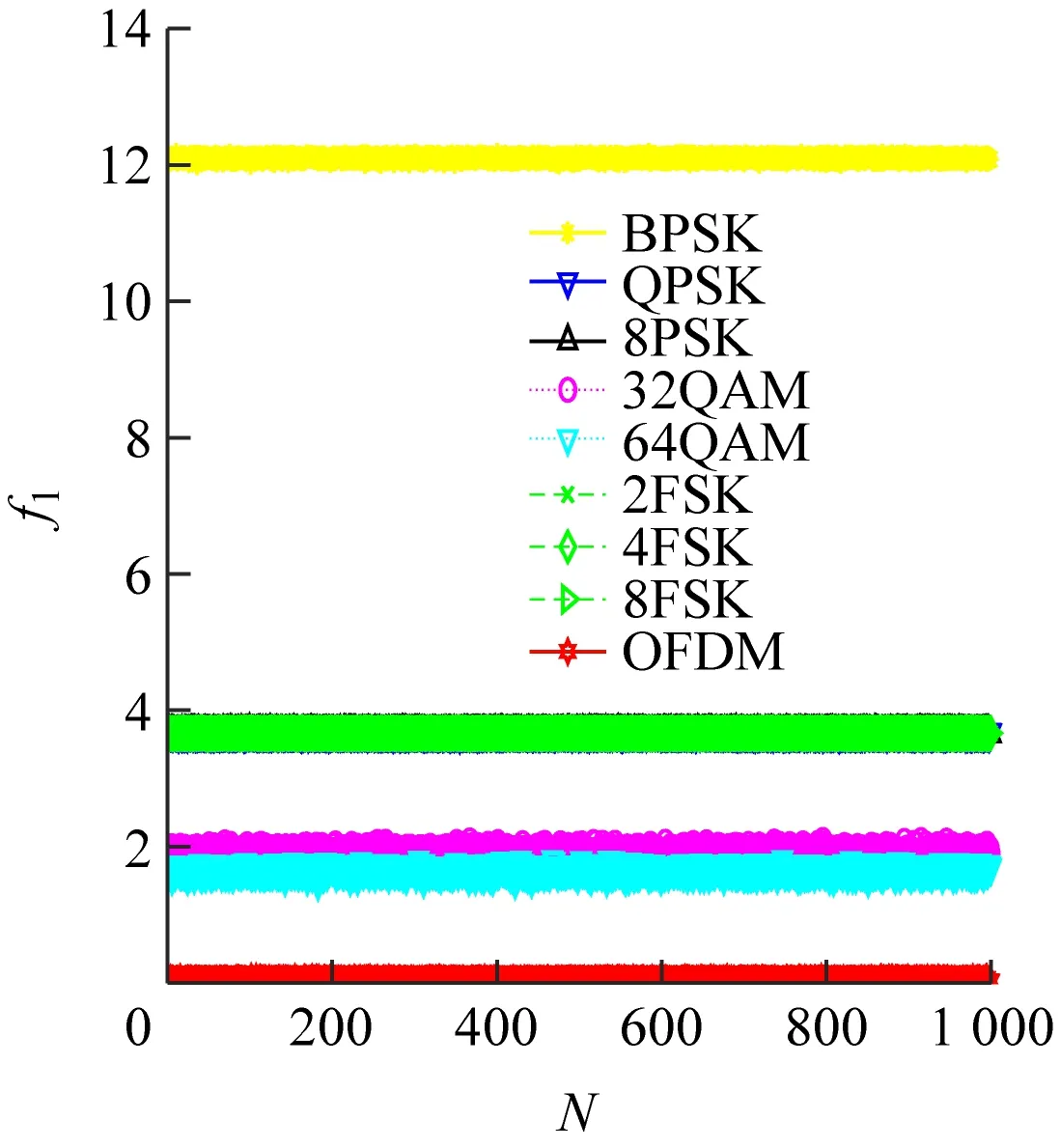
(d) 特征参数为f1,信噪比为10 dB

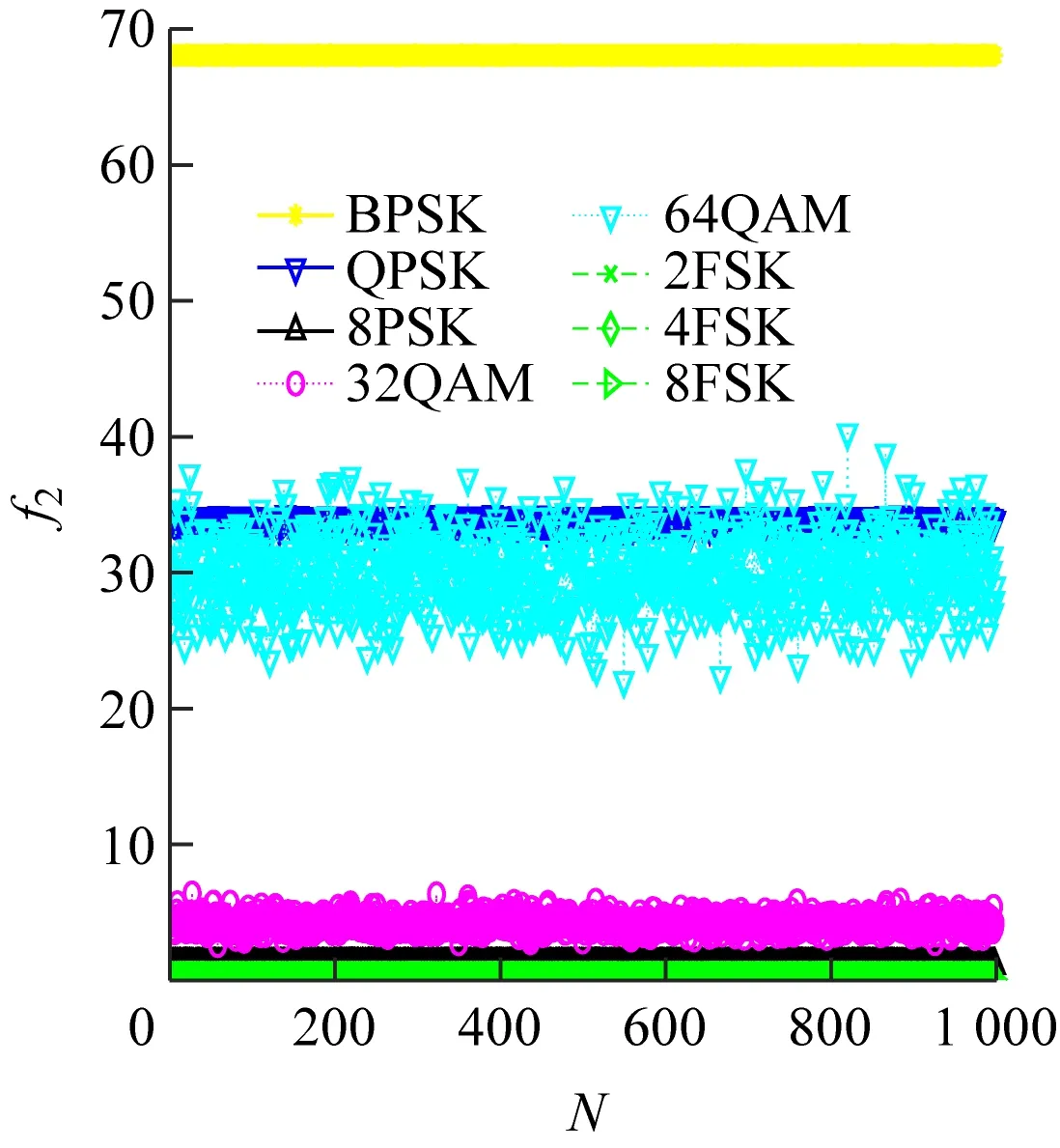
(e) 特征参数为f2,信噪比为10 dB

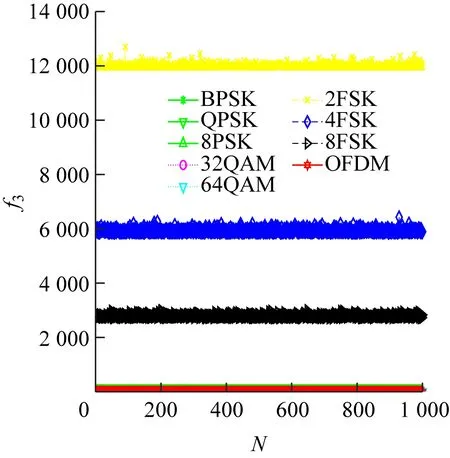
(f) 特征参数为f3,信噪比为10 dB

2 井下衰落信道下高阶累积量分析

矿井巷道围岩给无线通信信号制造了非常庞杂的反射和散射路径，到达通信接收端的信号都经过了反射、绕射和散射的多径信号叠加，导致接收端信号大幅波动。因此，研究井下信道模型对高阶累积量的影响是进行矿井下无线信号检测识别的前提。根据文献[12-13]对井下信道模型的分析，本文选取矿井环境应用较为普遍的衰落信道模型，即参数可变的Nakagami-m衰落信道模型，在Nakagami-m衰落下，接收信号包络r的概率分布密度函数为

(5)

Ω=2σ2=E(R2)=R2

(6)

(7)

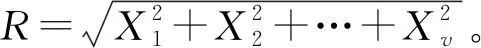
根据文献[12-13]，m=0.85，Ω=1时更接近矿井环境。

R的第k阶矩为

(8)

由式(8)可得出R的2阶矩、4阶矩、6阶矩及8阶矩分别为

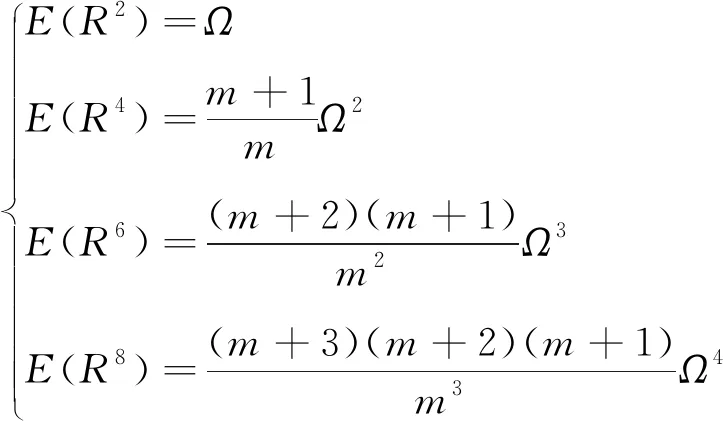
(9)

结合式(9)和式(2)，得到Nakagami-m衰落信道下的高阶累积量公式：

(10)

3 深度学习的分类器模型

深度神经网络模型具有优秀的学习能力，相比于决策树方法有更好的鲁棒性，与支持向量机(SVM)相比，能够更好地解决多分类问题。因此，本文选用常见的多层前馈神经网络(DNN)模型作为分类器。DNN模型如图2所示。

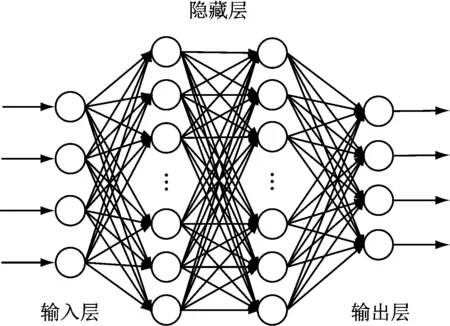
图2 DNN模型Fig.2 DNN model

对特征参数f进行归一化后，将其作为DNN模型的输入，归一化公式为

(11)

DNN模型分为输入层、2个隐含层和输出层。用f1、f2和f3组成一个DNN模型的输入向量。输出采用热独编码的形式。DNN模型中的激活函数采用线性整流函数，线性整流函数能够有效利用梯度下降算法优化目标函数。网络模型输出层选用归一化指数函数。对于信号调制识别问题，采用交叉熵损失函数作为代价函数:

(12)

式中：yi表示样本标签，包含调制方式种类和信噪比；z(fi,w)为神经网络模型输出；fi为神经网络输入；w为神经网络权重。

4 仿真分析

基于Matlab和Python平台进行仿真，调制信号仿真和特征提取在Matlab平台实现，神经网络构建和训练使用Tensor Flow机器学习软件库。制作2个数据集，分别用于高斯白噪声信道和矿井小尺度衰落Nakagami-m信道测试。每个训练集中包含每种调制信号特征26 000组(信噪比范围为-5～20 dB，信噪比步长为1 dB，对应每个信噪比下各调制信号特征为1 000组)，测试集中包含每种调制信号2 600组。选定每层神经元个数，输入层为3个，隐藏层为14个和10个，输出层为9个。将本文方法与文献[15-16]的方法进行对比。文献[15]首次分析了Nakagami-m(m=2，Ω=1)衰落信道对4阶累积量的影响，并采用SVM对4种调制方式进行识别。文献[16]针对矿井Nakagami-m(m=0.85,Ω=1)衰落信道下的调制识别问题，首次提出基于4阶累积量特征，采用粒子群优化SVM分类模型对井下4种调制信号进行识别。

4.1 高斯白噪声信道

在高斯白噪声信道下，DNN模型的平均识别正确率如图3所示，各信号的识别率见表2。信噪比为-5 dB时，本文方法与文献[15-16]中的方法平均正确识别率对比见表3。

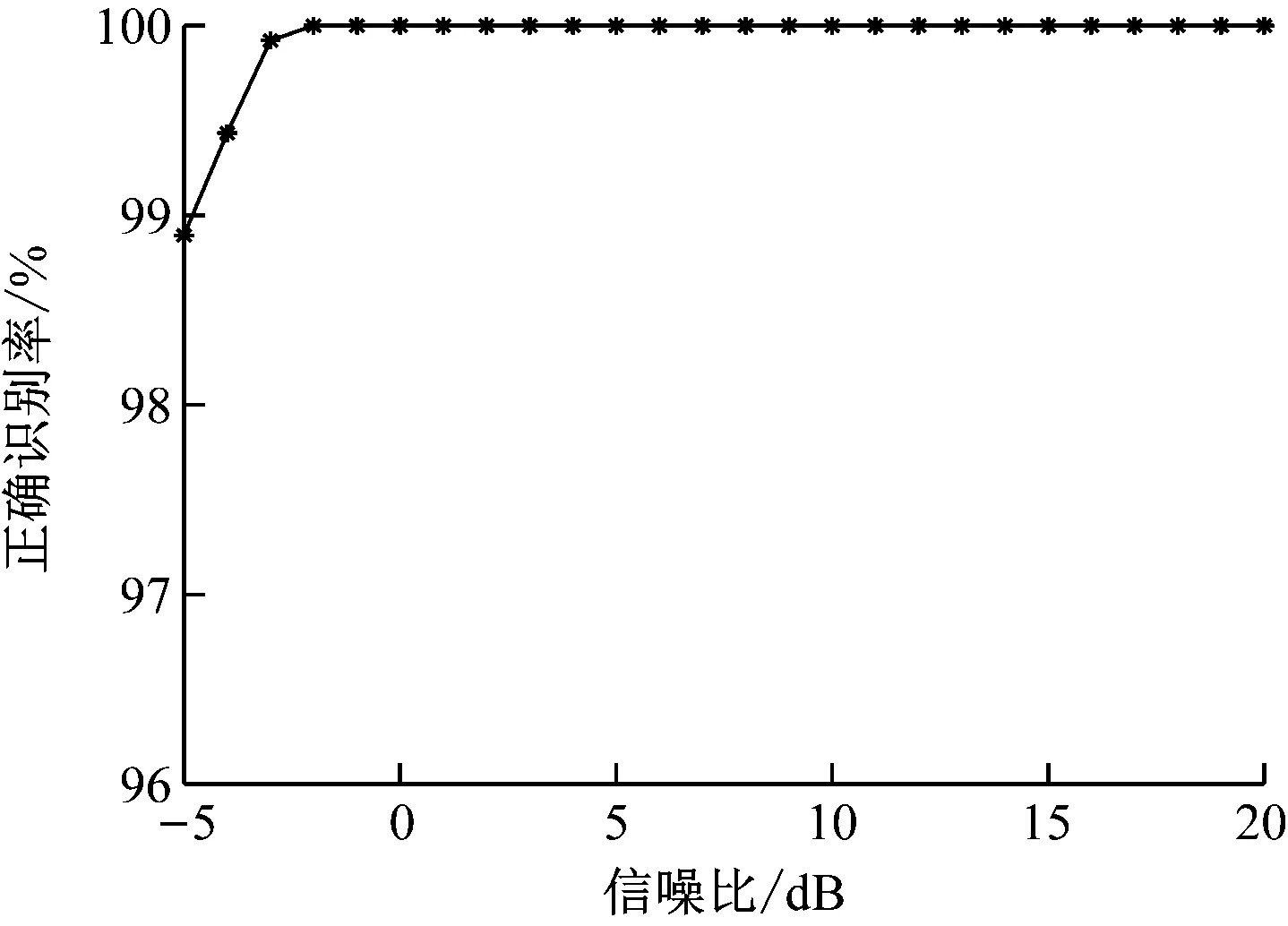
图3 高斯白噪声信道下的平均识别正确率Fig.3 Average recognition accuracy rate under Gaussian white noise channel

由表2可知，在高斯白噪声信道下，信噪比为-5 dB时，本文方法的识别率均能达到95%以上，信噪比为0 dB时所有信号的正确识别率都达到100%。由表3可知，在同样的信道环境下，本文方法比文献[15]和文献[16]中提出的方法分类效果更好。

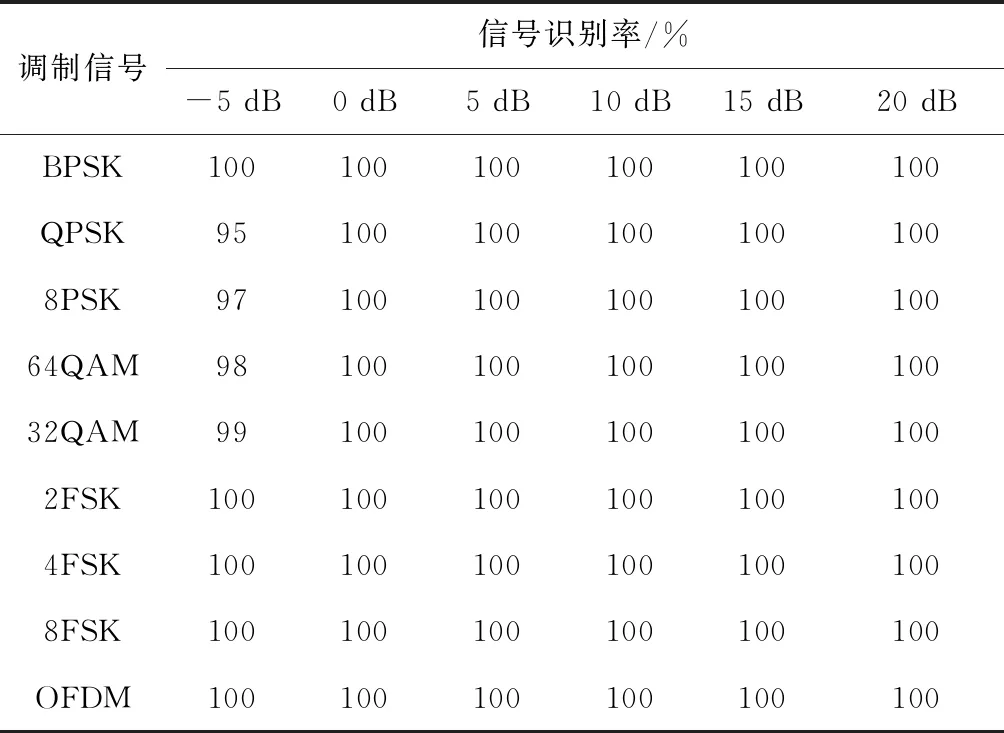
表2 高斯白噪声信道下的识别率Table 2 Recognition rate under Gaussian white noise channel

表3 不同方法识别率对比(高斯白噪声信道)Table 3 Comparison of recognition rate of different method (Gaussian white noise channel)

4.2 矿井下小尺度Nakagami-m信道

在矿井Nakagami-m衰落信道下，DNN模型的平均识别正确率如图4所示，各信号的识别率见表4，本文方法与文献[15-16]中的方法平均正确识别率对比见表5。

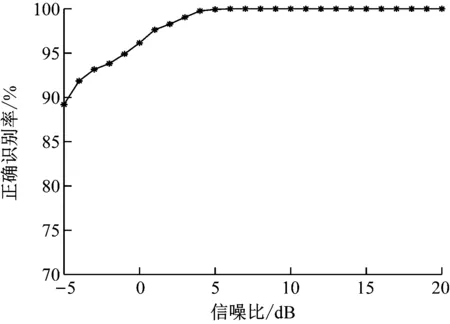
图4 矿井Nakagami-m衰落信道下的平均识别正确率Fig.4 Average recognition accuracy rate under mine Nakagami-m fading channel

从表4可知，在低信噪比下，对32QAM，64QAM的识别率较低，通过对比这2个信号在高斯白噪声信道下的识别率，可得出该类调制信号在矿井衰落信道环境下容易受到干扰。

表4 矿井Nakagami-m衰落信道下的识别率(m=0.85，Ω=1)
Table 4 Recognition rate under mine Nakagami-mfading channel (m=0.85，Ω=1)

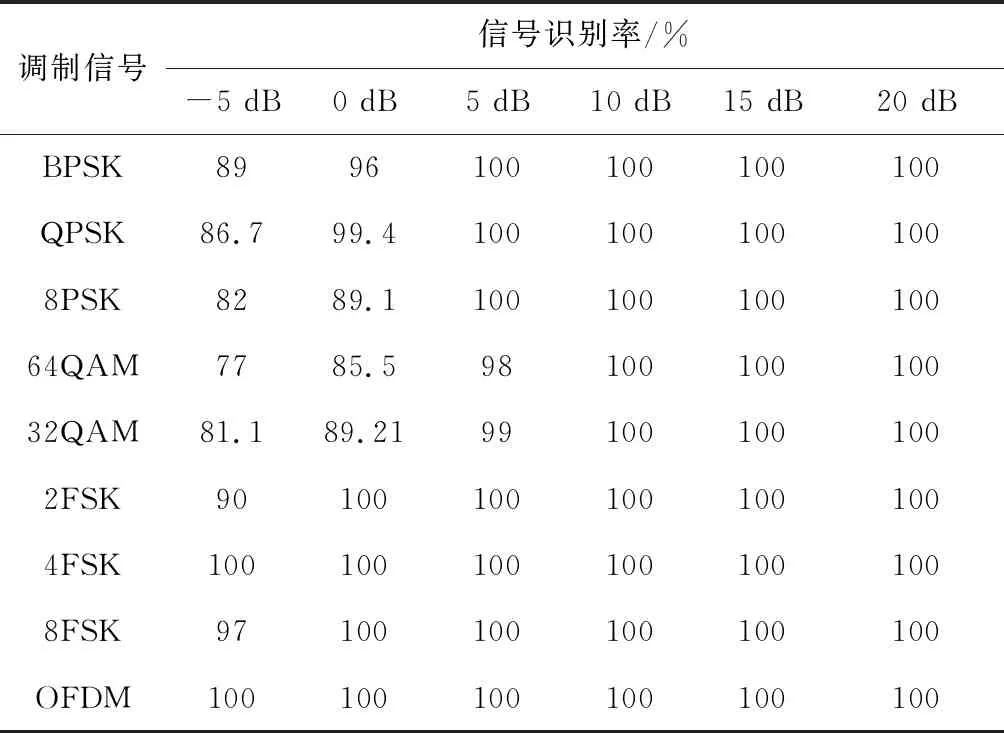
调制信号信号识别率/%-5 dB0 dB5 dB10 dB15 dB20 dBBPSK8996100100100100QPSK86.799.41001001001008PSK8289.110010010010064QAM7785.59810010010032QAM81.189.21991001001002FSK901001001001001004FSK1001001001001001008FSK97100100100100100OFDM100100100100100100

表5 不同方法识别率对比(Nakagami-m信道)Table 5 Comparison of recognition rate of different （References） (Nakagami-m channel)

文献[15]提出的SVM方法不需要事先知道信道的特性以确定门限值，不受信道类型的影响，但在低信噪比下识别率较低。文献[16]提出的方法在低信噪比下取得了较好的效果，但SVM性能的提升是以计算复杂度的增加为代价的。对比表3和表5可知，本文方法识别率更高，可识别的调制信号种类更多，且与文献[15-16]中的SVM分类器相比，省去了复杂的参数优化算法。

5 结论

(1) 通过高阶累积量理论分析得到BPSK，QPSK，8PSK，2FSK，4FSK，8FSK，32QAM，64QAM，OFDM共9种数字信号的高阶累积量理论值，发现MFSK的类内信号各阶累积量完全一样，无法直接利用累积量构造特征来实现信号识别。针对该问题，通过傅里叶变换提高信号辨识度。

(2) 分析井下信道模型对高阶累积量的影响，得到Nakagami-m衰落信道环境下的高阶累积量公式。根据高阶累积量理论值构造特征参数，选用常见的DNN模型作为分类器，对选取的9种数字信号进行识别。

(3) 仿真分析结果表明，基于高阶累积量和DNN模型的井下信号识别方法在矿井噪声环境下有较好的性能表现。与文献[15-16]的方法相比，该方法识别率更高，可识别的调制信号种类更多。在Nakagami-m衰落信道环境下，当信噪比为-5 dB时，该方法的平均正确识别率为89.2%以上，信噪比为5 dB以上时，平均正确识别率为100%。该方法为在特殊复杂环境下进行信号识别检测提供了新的思路，具有实用价值。