一种改进的三边定位算法
2020-02-28高莉杨雪苗
高莉, 杨雪苗
(1.江苏师范大学 电气工程及自动化学院, 江苏 徐州 221116; 2.中国矿业大学 信息与控制工程学院, 江苏 徐州 221116)
0 引言
目前,煤矿井下定位功能主要依托无线网络来实现[1]。由于无线网络中节点成本高、能耗大,在满足定位精度要求的情况下,从经济效益角度考虑,不适合在井下布置太多的节点作为定位系统的参考节点。三边定位算法能根据3个已知坐标的参考节点到未知节点的距离来确定未知节点的坐标[2-4],对参考节点数量需求低,能较好地满足煤矿井下定位系统经济性需求。理想的三边定位算法中,以参考节点坐标为圆心、参考节点到未知节点的测量距离为半径,可得3条相交于一点的圆曲线,未知节点坐标为3条圆曲线的交点。然而,受噪声、多径效应等因素影响,测量距离不可避免存在误差,导致3条圆曲线不会相交于一点,所以需要求解由3个圆曲线方程所构成的非线性方程组。
文献[5]采用非线性最小二乘(Nonlinear Least Squares,NLS)算法直接求解非线性方程组,其核心思想是利用类似高斯-牛顿法的搜索法来寻找代价函数的极小值,定位精度较高,但计算复杂度高,并且需要选择合适的初始值以避免发生局部收敛。文献[6-9]通过泰勒级数展开使非线性方程组在某组初始参数估计值附近线性化,降低了计算复杂度,但仍需要合适的初始值以保证收敛,且由于线性化过程中忽略了高阶项,无法保证得到最优解。文献[10-14]利用线性最小二乘(Linear Least Squares,LLS)算法将非线性方程组转化为线性方程组,之后通过最小二乘(Least Squares,LS)算法求解线性方程组,避免了初始值选择问题,但未考虑测距误差对定位结果的影响。文献[15]提出的加权最小二乘(Weighted Least Squares,WLS)算法根据测距误差赋予方程组中每个等式不同权值,提高了定位精度,但由于非线性方程组线性化过程会带来定位信息损失,定位精度还有提升空间。
本文提出了一种改进的三边定位算法。该算法以WLS算法估计的未知节点坐标为基础,融合线性化过程中所损失的定位信息,构建定位模型,通过求解该定位模型实现精确定位。
1 基于WLS的三边定位算法
假设二维平面分布3个参考节点,第i(i=1,2,3)个参考节点坐标为(xi,yi),未知节点坐标为(x,y),未知节点到第i个参考节点的测量距离为ri,则有
(1)
式(1)是一个非线性方程组,以第1个等式作为参考等式,通过其余等式减去参考等式的方法消除二次项,将式(1)转换为线性方程组,可得
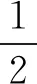
xi+yi)i=2,3
(2)
将式(2)写成矩阵形式:
Aθ=b
(3)
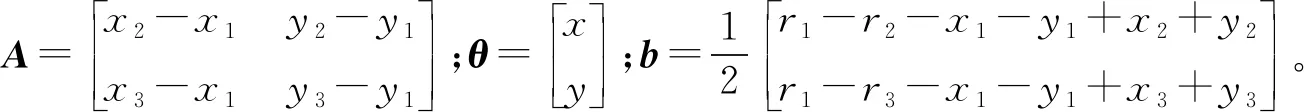
根据LLS算法,未知节点的LLS估计坐标为
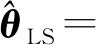
(ATA)-1ATb
(4)
在LLS算法求解式(3)的过程中,是将式(3)的2个等式按相同权重处理。然而实际中由于测距误差随机,每个等式对定位结果的影响不同。针对该问题,WLS算法引入权重矩阵W来提高定位精度,则未知节点的WLS估计坐标为
3.3.3 建立标准元数据规范。完善各系统的信息录入标准和元数据规范,包括:①新闻动态信息类:必须要有标题、副标题、作者、正文、来源(对于引用的文章,还需要注明来源或者出处)。正文内容字体大小需要统一样式规范。②文档类资源库表结构包括:文档编号、文档标题、副标题、文档正文、作者、来源日期等字段等。③调查调研指南规范:明确每项调研活动的名称、内容、调研主体、依据、条件、位置、时间和渠道等。④图片资源:包括图片id、标题、作者、人物、地点、时间、关键词、描述。⑤视频资源:包括视频id、标题、地区、发行年份、适用语言、标签、人物、来源、简介等字段。

(ATWA)-1ATWb
(5)
权重矩阵W可利用b的协方差矩阵C的逆来构建[15]:
W=C-1
(6)
假设测量距离ri之间相互独立,可得
(7)
式中var(·)为方差函数。
由于噪声、多径效应等因素影响,实际测量中不可避免地存在误差,则有
ri=di+ni
(8)
式中:di为未知节点到第i个参考节点的真实距离;ni为测距误差。
假设测距误差ni服从均值为0、方差为σi的高斯分布,即ni~N(0,σi),则测量距离ri~N(di,σi)。运用非中心卡方分布的方差,可得
var(ri)=4diσi+2σi
(9)
则式(7)可表示为
C=
(10)
由式(10)可知,权重矩阵中包含真实距离,然而实际计算中真实距离不可知,因此利用测量距离代替真实距离来构造权重矩阵。
基于WLS的三边定位算法在线性化过程中存在定位信息损失情况,具体如下。
展开并整理式(1),可得
(11)
将式(11)写成矩阵形式,并进行初等行变换,可得
(12)
对比式(12)和式(3)可看出,基于WLS的三边定位算法利用非线性方程组中1个等式作为线性化工具,将非线性方程组转化为线性方程组的同时,将作为线性化工具的等式的信息弱化,并未有效利用所有等式的信息,损失了部分定位信息,定位精度有待进一步提升。
2 改进的三边定位算法
改进的三边定位算法在基于WLS的三边定位算法求得初步定位结果的基础上,利用损失的定位信息构建定位模型:
(13)
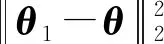
改进的三边定位算法步骤如下。
(1) 获取未知节点和参考节点之间的测量距离ri。
(2) 将参考节点坐标(xi,yi)和测量距离ri代入式(3),计算矩阵Α和b。
(3) 将测量距离ri替代di并代入式(10),计算协方差矩阵C,然后利用式(6)计算权重矩阵W。
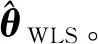
(5) 利用步骤(4)得到的结果及基于WLS的三边定位算法损失的定位信息,构建定位模型(式(13))。
(6) 根据式(13)求解未知节点坐标。
3 仿真分析
仿真区域部署如图1所示,区域长100 m、宽5 m,布置3个参考节点和10个未知节点,参考节点坐标分别为(-50,0),(0,5),(50,0),未知节点1—10随机分布。在测距误差标准差为2 m、仿真1 000次的情况下,基于WLS的三边定位算法与本文算法的仿真定位结果如图2所示。可看出基于WLS的三边定位算法平均定位误差为17.7 m,本文算法平均定位误差为7.9 m,本文算法的定位精度高于基于WLS的三边定位算法。
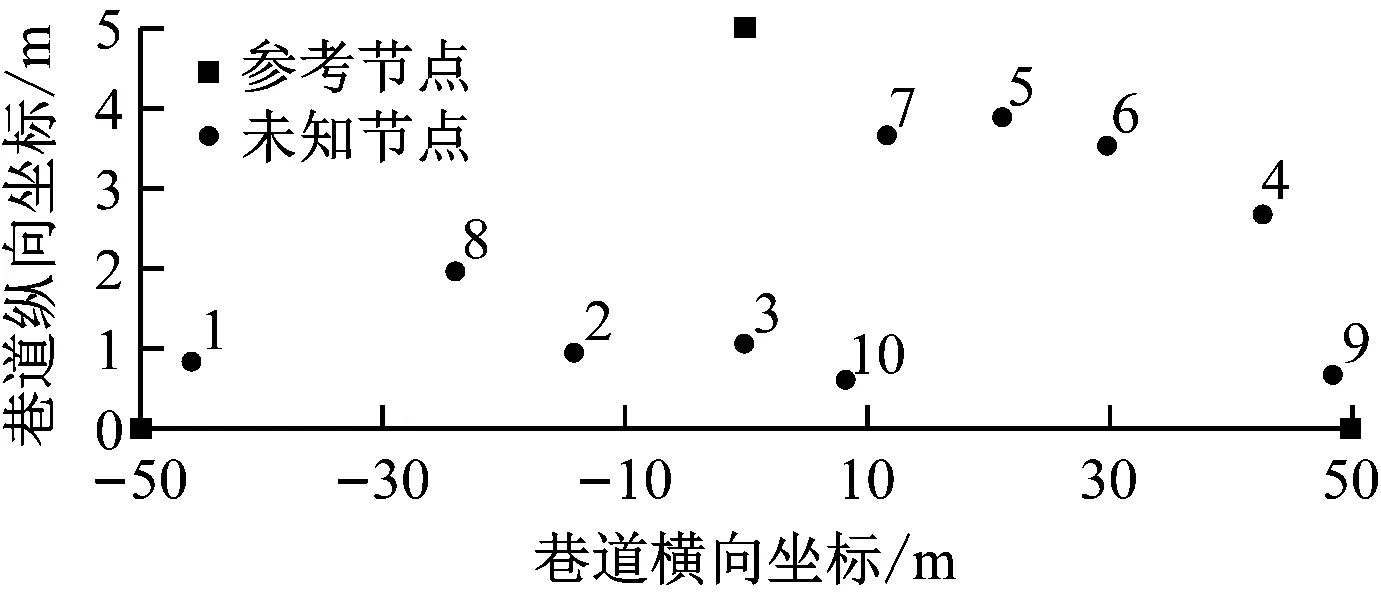
图1 仿真区域部署Fig.1 Simulation area deployment
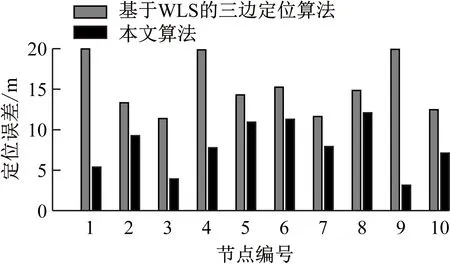
图2 不同位置定位结果Fig.2 Positioning results at different locations
基于上述仿真区域及参考节点坐标部署,设置未知节点坐标为(-30,4),测距误差标准差在0~10 m之间均匀取值,经过1 000次仿真,基于WLS的三边定位算法与本文算法的均方误差(Mean Square Error,MSE)如图3所示。可看出在测距误差标准差较小时,2种算法的MSE曲线接近;随着测距误差标准差增大,MSE均呈递增趋势,但本文算法的MSE更小,表明定位精度更高。这是由于测距误差标准差较小时,补偿的定位信息作用小,测距误差标准差较大时,定位信息的丢失对定位精度影响较大,而本文算法有效利用了丢失的定位信息。
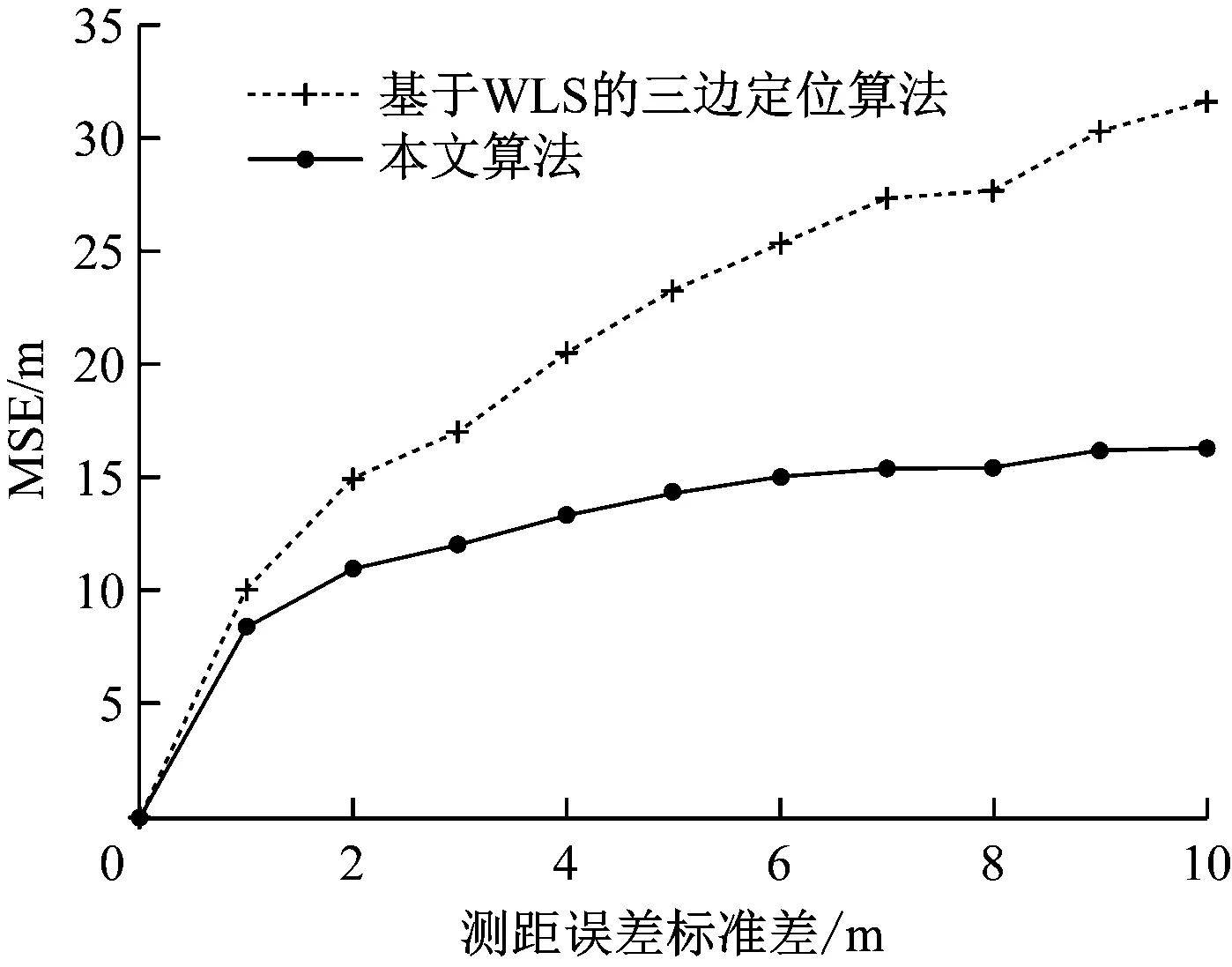
图3 不同测距误差标准差下MSEFig.3 MSE under different ranging error standard deviations
设置2种仿真区域及节点坐标:① 仿真区域长50 m、宽5 m,参考节点坐标分别为(-25,0),(0,5),(25,0),未知节点之间横向、纵向间隔均为2 m。② 仿真区域及参考节点坐标同图1,未知节点之间横向间隔为4 m、纵向间隔为0.2 m。给定测距误差标准差为1 m,仿真区域内各未知节点测试200次,基于WLS的三边定位算法与本文算法的均方根误差(Root Mean Square Error,RMSE)差值如图4所示。可看出在仿真区域几何中心点附近,RMSE差值较小,表明本文算法的定位精度虽有提升但不明显;距离中心点较远处,特别是左右两侧区域,RMSE差值较大,表明本文算法的定位精度明显提升。对比图4(a)和图4(b)可看出,在相同噪声情况下,仿真区域长宽比越大,本文算法的定位性能越好。
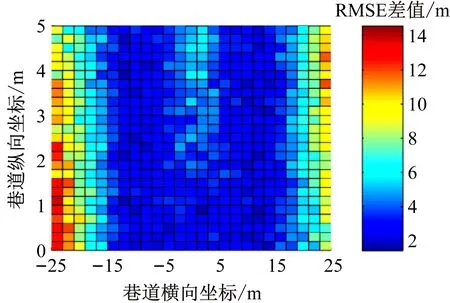
(a) 仿真区域长50 m、宽5 m

(b) 仿真区域长100 m、宽5 m
4 结语
改进的三边定位算法通过WLS算法粗略估计未知节点坐标,并利用损失的定位信息构建定位模型,通过求解该定位模型实现精确定位。仿真结果表明,该算法定位误差小于基于WLS的三边定位算法,定位精度得到明显提升,且巷道长宽比越大,定位性能越好。
