南疆小学生数学运算错误类型及分析——基于新疆大规模测评数据

何 伟，董连春，法 旭，邵 伟，郎甲机

南疆小学生数学运算错误类型及分析——基于新疆大规模测评数据

何 伟，董连春，法 旭，邵 伟，郎甲机

（中央民族大学 理学院，北京 100081）

结合新疆大规模测评数据，针对南疆小学生数学运算中错误进行了微观分析．研究发现，南疆小学生在整数乘法、整数除法、整数混合运算、小数加法、小数减法和小数混合运算6个方面出现错误类型主要表现为概念性错误，即混淆运算符号、不理解小数概念、混合运算中运算顺序混乱和运算律使用错误等问题．出现概念性错误的原因主要包括复杂运算的算法与算理的理解问题，对位值的理解问题和混合运算中运算规则的理解问题．

运算能力；运算错误；小学；数学；南疆

1 问题提出

数学运算是数学课程中“数与代数”部分的重要内容，同时也是支撑学生学习“图形与几何”“统计与概率”“综合与实践”3个部分的重要基础．《义务教育数学课程标准（2011年版）》将“运算能力”列为十大核心概念之一，并明确指出，“运算能力主要是指能够根据法则和运算律正确地进行运算的能力”[1]．小学生数学运算能力及其教学方法层面的研究，主要集中在运算错误的类型以及对策．王巍指出，小学生在出现计算错误时，教师往往会简单归因为学生不认真听讲、不够细心或者思维定势等原因，缺乏对学生运算错误背后深层次原因的剖析与指正[2]．孙兴华和马云鹏发现，小学生在数学运算方面出现错误的原因十分复杂，职初教师往往认识到学生错误的表层原因，而教学经验丰富的教师能够发现学生错误背后的深层次原因[3]．张树东在总结国内外研究的基础上，从心理学和教育学两个层面梳理了小学生出现运算错误的主要原因，包括缺乏概念性知识、工作记忆低下以及视觉—动作统合能力低下等[4]．

在中国的新疆，特别是南疆四地州，即和田地区、喀什地区、克孜勒苏柯尔克孜自治州和阿克苏地区，由于各种因素的影响，长期以来，学生在数学学习方面面临的问题较为突出[5-6]．研究者对新疆学生数学学业成就与诸多影响因素间的关联，进行了研究与探讨．例如，有学者指出新疆学生数学学业成就不佳与如下因素存在密切联系：教育投入、师资水平、学校办学形式（如寄宿制）、课程设置的难度、数学教材与新疆学生日常生活的联系、学生汉语水平、学生自我效能感、学生学习信念与学习习惯、学生学习方式等[5]．这些研究从宏观层面分析了新疆学生数学学业成就的影响因素，为教育政策的制定与调整提供了非常有价值的借鉴．

2016年5月，教育部和新疆教育厅联合开展了新疆双语教育质量监测工作[7]，南疆地区9 229名四年级小学生参加了数学测试．结果发现，南疆四地州四年级小学生在“数与代数”部分的平均得分率仅为50%，其中数学计算题目的平均得分率为51%，进一步反映出南疆四年级小学生数学运算能力非常薄弱这一问题的严重性．数学运算是小学阶段数学学习的重中之重，不仅影响到后续数与代数部分内容的学习，还会影响到其它模块的学习．因此，深入研究南疆四年级小学生数学运算错误十分必要．

基于以上分析，拟研究以下问题：南疆小学生在数学运算方面出现的具体问题有哪些？背后的原因何在？这些问题的回答，能够发现影响南疆小学生运算能力薄弱的根本原因，进而提出有针对性的解决方法．

2 研究方法

2.1 研究样本

2016年教育部与新疆教育厅联合开展新疆双语教育大规模质量监测项目，抽取南疆四地州310个班级共计9 229名四年级小学生，其中维吾尔族小学生占比97.6%．使用国家通用语言学习数学的学生比例约为80%，男女生比例接近1:1，农村学生比例约为80%．

南疆四地州中，阿克苏地区教育水平处于中等水平．因此从阿克苏地区参与测试的学生样本（总计2 085名学生）中，采用分层抽样与简单随机抽样相结合的方法，抽取660名四年级学生的测试卷．其中，维吾尔族学生比例99.5%，使用国家通用语言学习数学课程的学生约占80%，男女生比例约为47:50，乡村学生比例约为81%．抽取样本各方面比例与原样本比例基本一致，能够较好地代表南疆四地州学生的一般情况．研究对象具体信息如表1所示．

表1 研究对象具体信息

2.2 测试题目选取

表2 测试题目具体类型

2.3 编码分析与数据处理

结合已有研究[5-9]，将运算错误分为3类：概念性错误、程序性错误和协调性错误．概念性错误主要指学生在数学运算方面存在概念性的认知错误，如不能根据计算法则进行基本的运算；程序性错误是指，学生对数学运算有基本的概念认知，但是具体使用运算法则进行运算时，出现错误（比如进位错误或者借位错误）；协调性错误，主要是指学生对数学运算有基本的概念认知，能够依据运算法则进行运算，但是在运算过程中由于粗心产生的错误，如誊写错误或者遗漏数字错误．对加法、减法、乘法、除法、混合运算5种类型题目，将学生出现的错误分别编码为概念性错误、程序性错误和协调性错误，编码框架如表3所示．为保证编码一致性，由两位编码员对所有学生答案进行独立编码．而后对编码不一致的学生答案进行进一步讨论和分析，最终达成一致．

表3 具体编码框架

注：错误类型的具体解读，请参见下文．

3 研究结果

3.1 整体水平

660名学生样本中，全部（14道）运算题目的平均正确率为58%，具体每道题目的正确率情况如表4所示．可以发现，南疆四年级小学生在小数加减法部分的正确率相对较高，而在整数乘除法以及整数混合运算部分的得分率相对较低．特别地，整数混合运算部分两道题目的得分率均低于50%．此外，整数与小数混合减法的得分率也相对较低，3道题目中有两道题目的得分率低于50%．

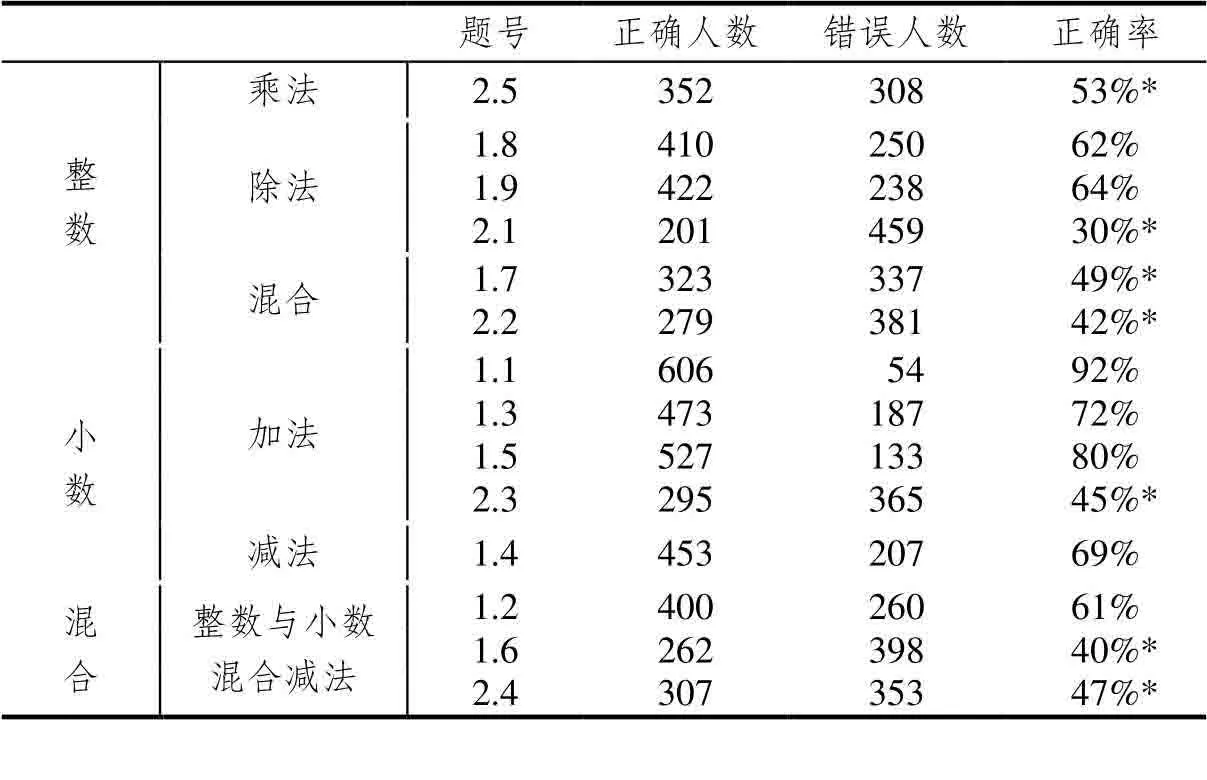
表4 新疆基础教育监测测试中计算题正确率

注：*表示得分率低于60%．

3.2 错误类型

图1给出了学生在整数乘法、整数除法、整数混合运算、小数加法、小数减法和整数小数混合减法6个方面的错误类型情况．可以发现，在每一类题目中，学生运算错误中概念性错误所占比例都超过了70%．对于整数乘法、整数除法和小数减法3个层面，学生的概念性错误比例超过了85%．

注：Z-MUL=整数乘法，Z-DIV=整数除法，Z-MIX=整数混合，X-ADD=小数加法，X-SUB=小数减法，MIX=整数小数混合减法．

由图1可见，学生在运算过程中出现的错误主要为概念性错误，反映出计算错误并非是简单的“不认真”和“不细心”，而是对算理和算法的理解存在很大的问题．

3.3 具体错误实例

通过学生作答的具体实例，从概念性错误、程序性错误和协调性错误3个方面展示学生在每个错误类型上出现的问题和障碍，并简要分析这些错误出现的原因．

3.3.1 概念性错误及原因分析

（1）混淆运算错误．

学生在小数加法与减法计算中的混淆运算错误见图2．

注：图中序号是为便于展示学生错误答案，非测试题目序号，下同．

学生在小数乘法与除法运算中的混淆运算错误见图3．

图3 概念性错误——混淆运算（二）

在图3（a）的5个例子中，学生将乘法按照加法进行运算，从而得出错误结果．尤其在例（3）、例（4）、例（5）中，题目中运算符号既有乘法符号，又有加法符号，但是学生仍旧将所有数字按照加法进行计算．在图3（b）中，有些情况是学生将除法混淆为减法，如例（1）、例（4），有些情况是学生将除法混淆为加法，如例（2）、例（3）．

（2）不考虑列错误．

学生在加法与减法运算中不考虑列的错误见图4．

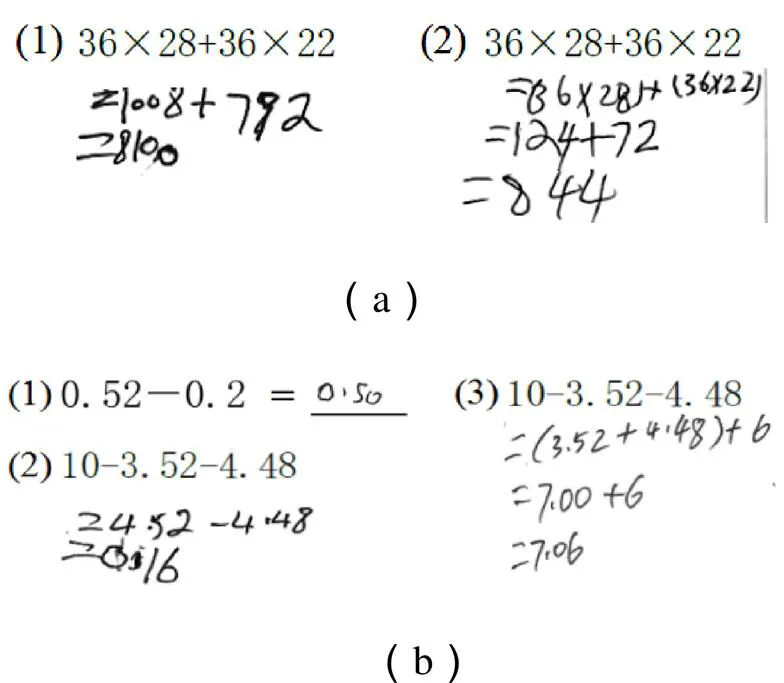
图4 概念性错误——不考虑列错误

图4（a）的例（1）中，学生在乘法运算结果得出之后，对1 008+792进行加法运算时，混淆了千位与百位，从而将正确结果由1 800写成8 100．又如图4（b）的例（1）中，学生在进行减法计算时，没有考虑列，从而将两个小数的末位对齐，而非小数点对齐，导致出现错误结果0.50．

（3）不理解小数概念．

学生在小数加法运算与小数减法运算中出现的“不理解小数概念”错误见图5和图6．

图5 概念性错误——不理解小数概念（一）

从图5中的例（1）可以很清晰地看出，当出现7.95+5.76时，学生将加号左边和右边的两组数字（即95和5）看作了加法的运算对象，并且用小括号将95+5放在一起，这说明学生并未理解小数与整数的区别．

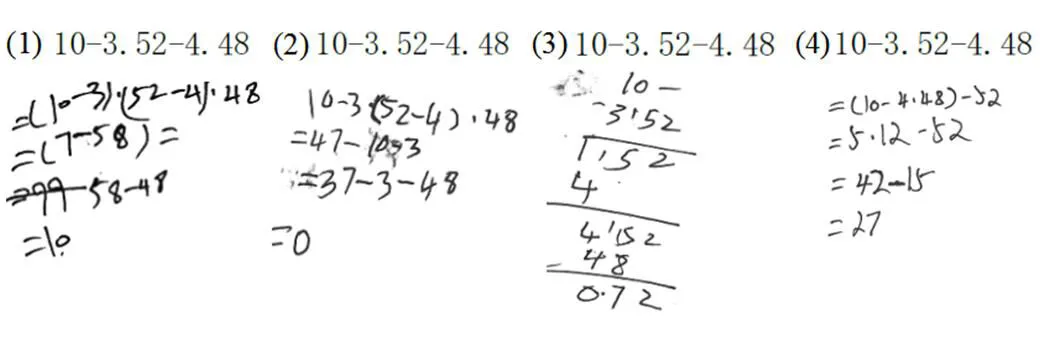
图6 概念性错误——不理解小数概念（二）

（4）计算顺序错误．

学生在混合运算中出现的计算顺序错误见图7．

图7 概念性错误——计算顺序错误

图7的例（1）和例（2）中，学生错误地按从左至右的顺序进行计算，未考虑乘法运算的优先原则．而例（3）中，学生考虑了优先进行乘法运算，但错误地改变了运算对象，导致问题产生．例（4）中，学生首先将36分解成4和9，28分解成4和7，但将9与后面的22直接相乘，出现错误．

（5）运算律使用错误．

学生在减法混合运算中出现的运算律错误见图8．

图8 概念性错误——运算律错误（一）

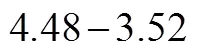
学生在乘除法的混合运算中出现的运算律错误见图9．

图9 概念性错误——运算律错误（二）

图9的例（1）（2）（3）（4）中，学生试图使用分配律进行运算，却仅将56与100进行乘法计算，忽略将56与1进行乘法计算．例（5）至例（10）中，学生试图使用乘法分配律进行计算，但出现各类错误，可见，学生并没有真正理解乘法分配律，只是从形式上记忆分配律的公式．

以上5种概念性错误，说明学生学习运算的过程中存在较为严重的滞后问题．通过分析学生在运算过程中出现的概念性错误类型，发现如下原因制约学生运算水平的提高．

第一，复杂运算的算法与算理的理解问题．例如，与加法和减法相比，乘法与除法的理解与计算更为复杂，认知要求更高．诸如混淆运算错误的出现，说明学生只能进行最为基础的加法运算和减法运算，而无法进行乘法和除法运算，这反映出学生在计算技能方面仍然停留在较低层次．南疆地区学生主要为维吾尔族学生，母语并非国家通用语言，因此，这种错误的出现，说明有效地理解复杂运算的算理与算法仍然是新疆基础教育中的一个难点．

第二，对位值的理解问题．运算过程中，数字的位置不同，代表不同的位值．出现进位、借位错误的部分原因可能是因为维吾尔语的书写顺序是从右向左，而数字书写顺序恰恰相反．母语书写顺序与数字的书写不一致问题，给学生理解位值带来了一定的困难．因此，在面向南疆学生的教学中，需要特别考虑学生在位值这一概念方面的理解障碍．同时，学生出现的对小数概念的理解误区，也反映出学生对小数表示中的位值理解存在较大的障碍．

第三，混合运算中运算规则的理解问题．混合运算过程中，涉及不同运算的优先级问题以及运算律的使用．学生出现运算顺序问题和运算律使用混乱等问题，反映出学生在数学学习中未能理解混合运算的运算规则，对运算律的认识停留在较浅的层次．

3.3.2 程序性错误及原因分析

（1）进位、借位错误．

学生在加法运算中的进位错误和减法运算中的借位错误见图10和图11．

图10中的例（1）没有进位，例（2）进了两位．例（4）中也没有进位，但是将8+2所得结果10放在了最后的计算结果当中，最后得出0.810的错误结果．例（5）中在计算17.95+1.05的过程中，没有向十分位进位，而是直接进位到了个位，导致出现19.90的错误．

图10 程序性错误——进位错误

图11 程序性错误——借位错误

（2）残迹错误．

学生在加法运算和减法运算中出现的残迹错误见图12和图13．这种错误是指学生在加法计算或者减法计算中会改变运算的对象．

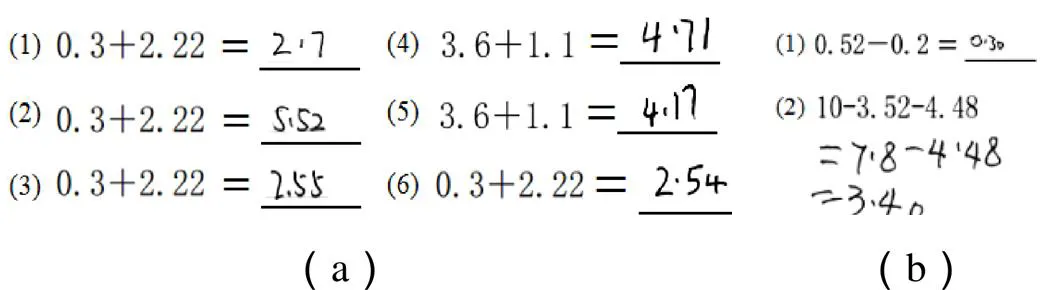
图12 程序性错误——残迹错误

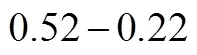
（3）空间排列错误．

学生在乘法运算中出现的空间排列错误见图13．

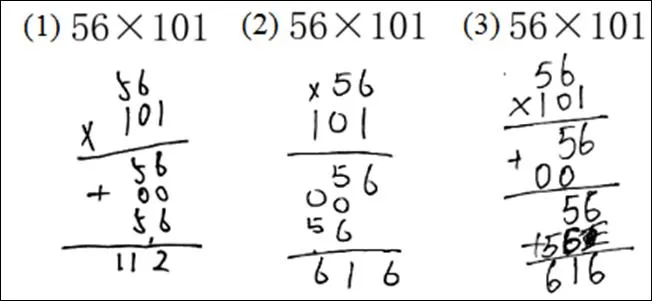
图13 程序性错误——空间排列错误

这种错误主要出现在学生使用竖式进行乘法计算的过程中．如图13的例（1）中，学生将3次运算结果对齐排列；例（2）和例（3）中，学生将前两次运算结果正确排列，但是将第三次的运算结果与第二次运算结果对齐排列．

（4）计算不完整．

学生在乘法和除法运算中的计算不完整错误见图14．

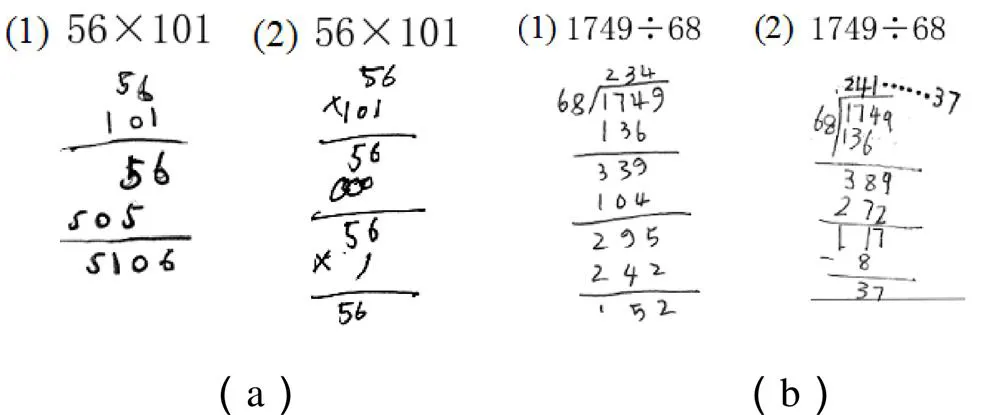
图14 程序性错误——计算不完整

图14（a）的例（1）中，第一次运算是56乘以1，第二次运算应该是50乘以0，但是学生却按照5乘以101的方式计算，然后将两次运算结果相加．图14（a）的例（2）中，首先将56与101的个位与十位进行计算，没有按照步骤进行完整的乘法计算．图14（b）的例（1）中，在得出117后，没有继续进行除法计算；例（2）中，在完成第一步运算，得出商的最高位后，没有继续完成后续计算．

（5）估商错误．

学生在除法运算中出现的估商错误见图15．

图15 程序性错误——估商错误

图15的例（1）中，在计算339除以68时出现估商错误；例（2）中，在计算389除以68时出现估商错误；例（3）中，计算174除以68时出现估商错误．

以上5种程序性错误表明，虽然学生对算法和算理达到了一定程度的理解，但在数学运算的准确性和熟练性方面存在问题，说明学生不能完整有效地完成笔算过程．此外，诸如“估商错误”等问题的出现，反映出学生在估算方面存在一定问题．实际上，估算水平的提高，离不开熟练的笔算技能这一前提条件．因此，学生出现程序性错误，反映出教学过程中对学生笔算技能熟练程度的培养存在较大提升空间．

3.3.3 协调性错误及原因分析

（1）誊写错误．

学生出现的誊写错误见图16．

图16 协调性错误——誊写错误

图16是学生在书写计算过程中，将运算对象写错，从而导致错误．例如，例（1）中，学生将7.95写成4.24；例（2）中，将7.95誊写成95；例（3）中，将1.05写成5.05．

（2）遗漏错误．

学生出现的遗漏错误见图17．

图17 协调性错误——遗漏错误

图17是学生在书写计算过程中，遗漏了小数点或某一数字，从而导致错误．3个错例中均出现遗漏小数点的错误．

（3）部分错误．

学生出现的部分错误见图18．

图18的例（1）中，在计算4.24+7.95与5.46+1.05时都是正确的，而在计算12.19+6.81时出现错误．

图18 协调性错误——部分错误

学生出现以上3种协调性错误，主要的可能原因是学生平时书写运算过程不规范，尤其是面对较多或较大数字的运算问题．这种情况通常被归结成学生“粗心马虎”等原因．但是以往研究[10]也指出，这些错误也可能是因为学生对运算法则进行机械记忆，从而无法自己察觉到出现的错误．

4 结论与讨论

南疆四年级小学生数学计算方面的主要障碍是缺乏对运算对象和算理算法的基本理解，计算中出现错误的主要类型是概念性错误，而非马虎等简单归因．这反映出学生对数学运算、运算对象、算法算理缺乏基本的认识和理解．

算法和算理的理解一直以来是小学数学教学的重点和难点，南疆小学生在这方面存在障碍也在情理之中．但是研究发现，南疆四年级小学生所犯概念性错误中出现大量的混淆运算符号（如将加法按照减法进行计算或者将乘法按照加法计算）、不理解小数概念（忽视小数中的小数点，将小数看成两个整数进行计算）、混合运算中运算顺序混乱等问题．反映出很多学生的数学学习在一定程度上存在低效性问题，考虑到参加测试的小学生处于四年级期末阶段，可以预想这些学生在升入五年级甚至初中时，运算方面的问题会严重影响其数学学科其它模块的学习，是最令人堪忧的问题．这些问题的出现可以归结成3方面原因．

第一，南疆地区教学水平有限．学生在运算中出现的概念性错误和程序性错误，反映出数学教学未能帮助学生理解相应的算理算法，未能帮助学生有效地提升数学运算的熟练性与准确性．从研究结果看，学生出现的计算错误，反映出当地教学水平的有限和师资力量的薄弱．这与以往研究者[11]的观点相同，反映出南疆地区学生学业水平的提高，离不开师资的改善．

第二，教学语言、学生母语不一致现象．不可否认，内地发达地区学生在运算能力方面也存在一定的问题，但是相比较而言，以往研究很少指出内地发达地区学生在运算方面存在较严重的概念性错误．该研究的发现，说明数学运算中的概念性错误突出这一问题具有一定的地域特点．其背后的主要原因可能是学生的母语与教学语言不一致，导致学生在数学学习过程中面临一定的语言理解障碍．在南疆地区，除了小部分学生使用母语学习数学知识外，绝大部分学生都在使用国家通用语言版本的教材，并且课上使用国家通用语言学习数学．在使用国家通用语言学习数学的过程中，南疆小学生既要应对非母语授课语言障碍的问题，又要掌握数学学习中的重难点知识．两方面的压力使得南疆小学生在数学学习中面临双重挑战．

第三，维吾尔语的特点．维吾尔语言中数字读法较为复杂，例如1.314读作“一点整千分之三百一十四”．而以往研究[12]指出，学生在学习过程中往往会读成“一点三百一十四”，这造成了学生在小数与整数的认知上产生一定程度的混乱．该研究中发现，学生在小数运算过程中出现较多的问题．这在一定程度上反映出，以维吾尔语为母语的小学生受母语语法特点的影响，给数学学习带来一定的负迁移．除此以外，维吾尔语书面语中，普通文本的书写顺序是从右向左横写，而阿拉伯数字的书写却是从左向右，这种差异给学生理解数学概念（比如位值）带来了一定的困难．

当前，越来越多的学者参与到中国少数民族数学教育研究与实践中[13-15]，极大地推动了少数民族数学教育发展．在以往研究基础之上，深入分析南疆四年级小学生的运算错误，反映出了南疆小学数学教学中存在较大的问题．南疆地区维吾尔族人口比例高达87%[16]，维吾尔族儿童的母语并非国家通用语言，但是随着新疆推行国家通用语言教学，绝大部分维吾尔族小学生都在使用国家通用语言学习数学知识．因此，后续研究应该从新疆基础教育实际出发，研究南疆小学数学教学中存在的问题，有效地利用学生出现的困难与错误，深入分析学生的想法并诊断出具体问题所在，进而有针对性地开展南疆小学数学教师培训，提高南疆数学教学的整体水平．

[1] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：6．

[2] 王巍．小学生数学错误的类型及对策[J]．课程·教材·教法，2014，34（7）：83-86．

[3] 孙兴华，马云鹏．小学数学教师如何处理学生计算错误的研究——以两位数乘两位数为例[J]．数学教育学报，2016，25（5）：38-44．

[4] 张树东．小学生计算错误的原因分析及对策[J]．教育研究与实验，2006（5）：53-58．

[5] 阿力木·阿不力克木．影响新疆维吾尔族中小学生数学成绩的内在因素研究[J]．民族教育研究，2011，22（6）：29-31．

[6] 阿布地莎，阿依丁，木尼拉．新疆伊犁地区哈维“实验班”数学教学调查研究[J]．数学教育学报，2007，16（1）：59-62．

[7] 教育部民族教育发展中心，新疆维吾尔自治区双语教育质量监测评价中心．新疆双语教育质量监测结果报告（小学阶段）[R]．2016-11：3-5．

[8] 刘加霞．小学数学有效学习评价[M]．北京：北京师范大学出版社，2015：34-35．

[9] 伍鸿熙．数学家讲解小学数学[M]．北京：北京大学出版社，2015：32-40．

[10] 张丹．小学数学教学策略[M]．北京：北京师范大学出版社，2015：61-62．

[11] 何伟，孙晓天，贾旭杰．关于民族地区数学双语教学问题的研究与思考[J]．数学教育学报，2013，22（6）：16-19．

[12] 莎吉旦木·买买提依明．维汉双语数学教学中的语言问题研究[D]．乌鲁木齐：新疆师范大学，2013：17-19．

[13] 薛德军，杨美主．甘肃舟曲藏族女性服饰中蕴含的数学文化探析[J]．数学教育学报，2018，27（2）：82-86．

[14] 陈婷，徐冉冉．中国少数民族数学教育的“现状”“问题”及“对策”——2017年全国少数民族数学教育研讨会暨西藏数学教学改革研讨会会议纪要[J]．数学教育学报，2018，27（1）：96-98．

[15] 杨梦洁，王彭德，杨泽恒．白族文化中数学元素的挖掘[J]．数学教育学报，2017，26（2）：82-86．

[16] 阿克苏行政公署政府网．阿克苏概况[EB/OL]．（2018-01-01）[2018-12-11]．http://www.aks.gov.cn/zjaks/xsgk/ aksdqgk/index.html．

A Study of Calculation Mistakes Made by Primary Students in South Xinjiang——Based on Xinjiang Large-Scale Assessment

HE Wei, DONG Lian-chun, FA Xu, SHAO Wei, LANG Jia-ji

(College of Science, Minzu University of China, Beijing 100081, China)

This study conducted a fine-grained analysis of the calculation mistakes made by primary students in South Xinjiang. It found that conceptual errors constituted the majority of the errors made by students in all the six content areas, namely multiplication of the whole numbers, division of the whole numbers, addition of the decimal numbers, subtraction of decimal numbers, and mixed addition and subtraction of decimal numbers. The conceptual errors mainly consisted of misconception of operations, misunderstanding of decimal numbers, order of operations, and so on. The reasons for the conceptual errors mainly included inability of understanding sophisticated computation and algorithms, inability of understanding the place value, inability of understanding the algorithms of mixed computation.

mathematics calculation; calculation mistakes; primary school; mathematics; Southern Xinjiang

2019-10-10

北京市教育科学规划课题——北京市中学内地新疆班、西藏班办学现状与对策研究（AAA14005）

何伟（1963—），女，蒙古族，黑龙江齐齐哈尔人，教授，主要从事数据挖掘、少数民族数学教育研究．董连春为本文通讯作者．

G623.5

A

1004-9894（2020）01-0070-06

何伟，董连春，法旭，等．南疆小学生数学运算错误类型及分析——基于新疆大规模测评数据[J]．数学教育学报，2020，29（1）：70-75．

[责任编校：张楠、陈隽]