基于Ant-agent的自动化码头AGV控制算法

兰培真，陈锦文，曹士连

(1.集美大学海上交通安全研究所，福建厦门361021；2.交通安全应急信息技术国家工程实验室，福建厦门361021)

0 引 言

自动化码头AGV 运输系统高效稳定地运行及合理地调度对于提高自动化码头的作业效率有着非常重要的意义.持续增长的港口吞吐量需要更多的自动导引车(简称AGV)分担集装箱水平运输任务.由于土地资源限制，AGV系统的运输路网难以进一步扩大，使得AGV 路径冲突和道路死锁问题日益凸显.

对于解决自动化码头AGV 路径冲突和道路死锁的研究集中在静态路径规划和动态路径规划两方面.文献[1-4]利用约束条件对AGV 行驶进行限制，求得目标函数的最优解规划其行驶路径，然而该方法无法有效解决路径冲突和突发状况，在长时间的运输作业下效率较低；文献[5-6]利用区域控制策略可避免AGV 间的路径冲突，但针对紧急情况无法实现安全的动态路径规划；文献[7-8]使用时间窗算法实现了AGV 的动态路径规划，但运输任务量较大时，无法有效解决路径冲突问题，AGV 停车等待时间较长.因此，一种实时避免AGV路径冲突和解除道路死锁的方法对提高自动化码头集装箱的水平运输效率至关重要.

文献[9-10]利用蚁群算法实现了对单一机器人的动态路径规划，但此方法针对自动化码头的多AGV 控制，难以实现全局最优.本文根据自动化码头AGV 运输系统作业的特点，仿照蚁群觅食行为，提出一种基于Ant-agent 的AGV 控制算法，实现多AGV 的实时运动控制，解决路径冲突和道路死锁问题，提高集装箱的水平运输效率.

1 AGV路径选择

1.1 AGV运输系统

自动化码头内集装箱的水平运输由中控系统向AGV 运输系统(简称系统)内的所有AGV 发送指令完成，本质上为集中式结构的多agent 系统(Multi-agent System，MAS)[11].由于不同种类的系统控制AGV 的方式均不同，故对算法及模型研究的系统提出以下假设：

(1)系统为集中式结构的MAS，一切指令由中控系统发送至各AGV.

(2)系统内各AGV之间无任何信息通讯.

(3)系统的运输路网由路段和节点构成.

(4)各路段不允许两台及以上AGV并列行驶.

(5)各节点不允许两台及以上AGV同时经过.

(6)不考虑环境、天气等外部不可控因素对系统的影响.

1.2 Ant-agent与拥挤度

蚁群算法仿照蚁群觅食，让蚂蚁通过释放信息素来搜索路径，若将AGV 视为Ant-agent，让AGV 具备蚂蚁的各项特性，则中控系统可根据信息素浓度实时判断路网状况，结合各辆AGV 当前位置和目标位置向其发送指令进行集装箱运输.本文将蚁群算法融入MAS，提出了一种基于Antagent 的AGV 控制算法，实现对AGV 运输行驶的实时控制.

AGV 运输系统需同时控制多辆AGV 在运输路网上行驶，若与传统蚁群算法相同，信息素为正反馈机制，AGV 将产生路径冲突和碰撞.同时，由于各路段交叉点间的距离较长，同一时刻同一路段上的不同位置能够感知到的信息素浓度均不同，若将路段作为信息素载体，无法准确表示此路段对各AGV 的排斥程度.故对Ant-agent(AGV)提出如下限定：

(1)信息素具有负反馈机制，对同伴产生排斥效应.

(2)每个Ant-agent 均携带相同浓度λ的信息素进入运输路网，在运输过程中，信息素不释放，浓度不改变.

(3)距离越远感知到的信息素浓度越低.

(4)利用路径交叉点感知信息素，信息素浓度之和为该点的拥挤度.

为实现对AGV 的实时控制，采用拥挤度实时全局更新策略，各节点的拥挤度根据每一时刻运输路网内所有AGV的位置进行更新.

式中：n为t时刻运输路网内AGV 的数量；为t时刻第k辆AGV与点(i,j)间的直线距离.

1.3 AGV的状态转移规则

由于存在停车以避免路径冲突的情况，AGV的状态分为停车等待和选择下一路径点两类.设AGV在节点(i,j)处的下一路径点的集合为(I′,J′)，

节点(i′,j′)处的拥挤度越高，选择此节点为下一路径点发生路径冲突和碰撞的可能性越大，引入拥挤度阈值q来规避AGV 间的碰撞.当τ(i′,j′)=0时，表明节点(i′,j′)周围无AGV 作业，选择此节点为下一路径点不存在碰撞危险；当τ(i′,j′)=λ时，表明节点(i′,j′)感知到的信息素浓度之和为λ，等价于此节点处有1 辆AGV，若选择此节点为下一路径点，极易发生碰撞.因此，本文将拥挤度阈值的范围设定为(0,λ).设allowedk为N(k)AGV的下一路径点集合，表示第k辆AGV.若τ(i′,j′)(t)＜q，则 以(i′,j′)为下一路径点发生碰撞的可能性较小，不影响运输系统的正常运行，(i′,j′)∈allowedk；若τ(i′,j′)(t)≥q，则以(i′,j′)为下一路径点发生碰撞的可能性较大，会影响系统的正常运行，(i′,j′)∉allowedk.若allowedk=∅，则N(k)AGV停车等待；若allowedk≠∅，则N(k)AGV选择下一路径点.

AGV路径点的选择与待选节点的吸引程度和启发函数有关.以拥挤度阈值q与时刻t节点(i′,j′)处信息素浓度τ(i′,j′)(t)的差值来表示节点(i′,j′)对AGV的吸引值，即

传统蚁群算法将当前节点与下一节点间的能见度作为启发函数[1-2]，但存在控制对象难以快速接近目标的缺点.建立两类启发函数和，分别表示AGV当前所在节点(i,j)与下一节点(i′,j′)间的能见度和下一节点(i′,j′)与目标点(ex,ey)间的能见度，即

式 中：为节点(i,j)与节点(i′,j′)的直线距离；为节点(i′,j′)与目标点(ex,ey)的直线距离.

的状态转移概率为

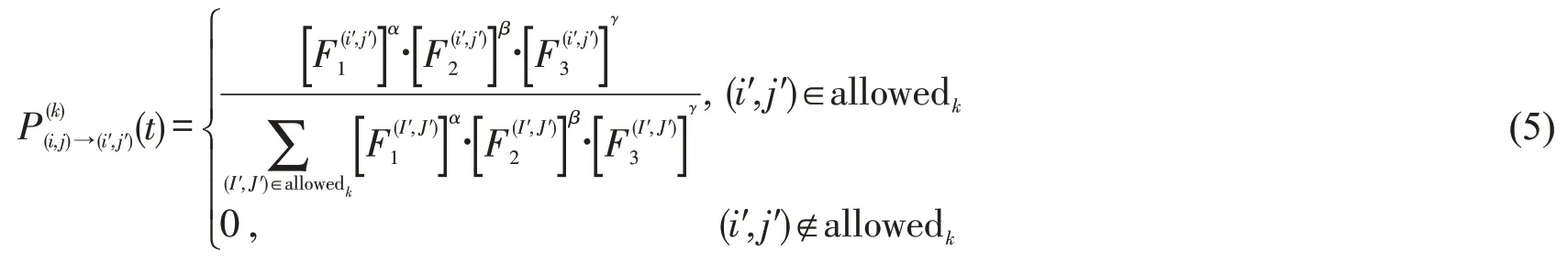
式中：为t时刻从节点(i,j)转移至节点(i′,j′)的概率；α,β,γ分别为节点吸引函数，两类启发函数和的重要程度系数.根据式(6)确定下一路径点(i′0,j0′).

2 冲突检测及解决机制

拥挤度阈值q可规避如图1(a)所示的节点冲突.

令

式中：为到达节点(i′,j′)的时刻；dsafe为AGV间的安全距离；v为AGV的行驶速度.

若同时满足式(9)和式(10)，即在t时刻，和(a,b为AGV 编号)分别从(i,j)和(i″,j″)同时驶向(i′,j′)且到达节点(i′,j′)的时间间隔小于行驶安全距离所需时间，则中央控制系统判定两辆AGV产生节点冲突，如图1(b)所示.

若同时满足式(10)～式(12)，或式(13)～式(15)，或式(16)～式(18)，则中央控制系统判定存在路径拥堵，分别如图1(c)，图1(d)和图1(e)所示.

图1 路径冲突示意图Fig.1 Diagram of path conflict

针对节点冲突，利用冲突节点对两辆AGV 的综合吸引值进行比较，以确定此冲突节点为哪辆AGV的下一路径点.冲突节点(i′,j′)对的综合吸引函数为

式 中：为节点(i′,j′)对的吸引值；为当前位置与节点(i′,j′)间的能见度；为 节点(i′,j′)与目标节点间的能见度.

设定如图2所示的映射f：A→B.

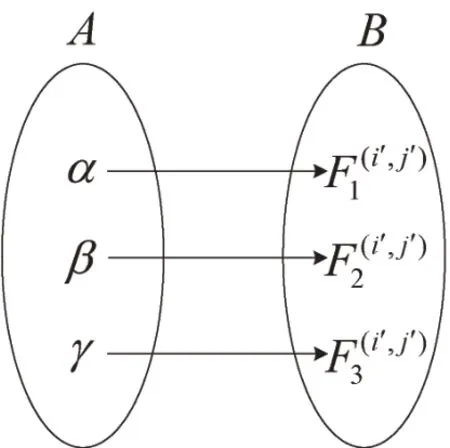
图2 映射示意图Fig.2 Diagram of mapping

通过式(20)～式(22)依次确定α、β、γ的最大值μ、中间值ξ、最小值φ，根据式(23)～式(25)确定第一优先级函数P1，第二优先级函数P2，第三优先级函数P3.

首先比较的第一优先级函数P1k.若P1a ＜P1b，则冲突节点(i′,j′)为的下一路径点；若P1a ＞P1b，则冲突节点(i′,j′)为的下一路径点；若P1a=P1b，则逐级依次比较P2a与P2b、P3a与P3b.若P2a=P2b且P3a=P3b，则中控系统随机决定哪辆AGV 选择(i′,j′)为下一路径点；另一辆AGV在其allowed中选择其余节点，若allowed中无其他节点，则停车等待.

针对路径拥堵，中控系统将两AGV 之间的距离控制在安全距离dsafe后停车.

3 算法设计

根据自动化码头AGV 运输系统的运营模式，结合状态转移规则和冲突解决机制，提出基于Ant-agent 的自动化码头AGV 控制算法(简称Antagent算法)，流程如图3所示.

图3 Ant-agent 算法流程图Fig.3 Flow chart of Ant-agent algorithm

4 算法验证及性能分析

4.1 算法性能评价及仿真环境

参数q，α，β，γ直接影响AGV 的路径选择、局部死锁的解除和集装箱的水平运输效率，因此利用表1中3项指标衡量算法的性能.

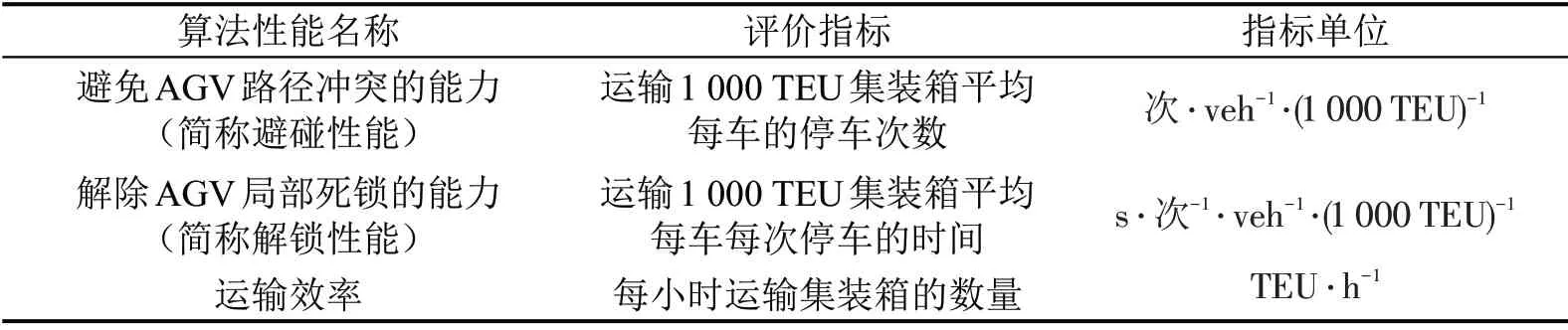
表1 算法性能及对应指标Table1 Algorithm performance and corresponding indicators

蚁群算法中，当信息素和启发式函数的重要程度均位于区间[1,5]时，算法的性能较优[13-14].结合拥挤度阈值q的范围，将初始试验参数设置为

共有4 个参数，每个参数包含9 个水平.为以较少的试验次数获取精确的最优参数组合，分两个阶段，采用均匀设计法进行试验，以全局最优为选择依据，确定运输效率最高时的参数组合最优，每个参数组合取10 次试验的平均值为最终结果，具体试验方案如图4所示.

在Netlogo 6.1.0中，参照某自动化码头的布局和实际数据构建如图5所示仿真环境，包含3个双小车岸桥(STS)装卸点，24 个自动化轨道吊(ARMG)装卸点和18 台AGV.AGV 由ARMG 行驶至STS 的上行速度为5.8 m ⋅s-1，由STS 行驶至ARMG的下行速度为3.5 m ⋅s-1，安全距离为10 m.

图4 两阶段均匀设计试验流程图Fig.4 Flow chart of two-stage uniform design experiment

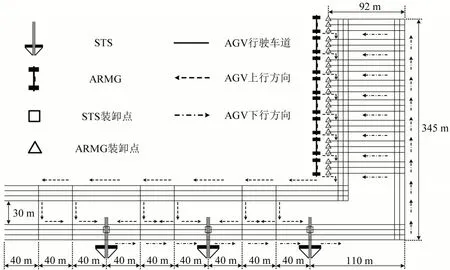
图5 AGV 运输路网图Fig.5 Diagram of AGV transportation road network

4.2 验证结果与对比分析

采用如图4所示的方法找出不同运输任务量下算法的最优参数组合，实现算法在不同运输任务量下的自适应调整，结果如图6所示.

图6 参数自适应变化曲线图Fig.6 Curve of parameter adaptive change

当运输任务量小于12 000 TEU 时，α在[5.4,5.5] 内波动，β在[0.5,0.6] 内波动，γ在[3.9,4.4] 内波动，q在[0.26λ,0.31λ] 内波动；当运输任务量大于等于12 000 TEU时，α=5.4，β=0.6，γ=4.4，q=0.26λ.由图6可以看出，随着运输任务量的增大，下一节点与目标节点间能见度的重要程度系数γ显著增加，拥挤度阈值q略有减小，同时算法参数的自适应调整趋于稳定.

将有两类启发函数F2和F3的Ant-agent 算法(Ant-agent algorithm with two types of heuristic function，Ant-agent-2hf)与只有当前节点与待选节点间启发函数F2的Ant-agent 算法(Ant-agent-hf)，文献[8]提出的基于时间窗改进Dijskra的动态路径规划算法(TW-Dijskra)在不同运输任务量下进行性能对比，结果如图7～图9所示.

图7 避碰性能对比Fig.7 Comparison of collision avoidance performance

图8 解锁性能对比Fig.8 Comparison of unlock performance

图9 运输效率对比Fig.9 Comparison of transportation efficiency

各运输任务量下，Ant-agent-2hf较TW-Dijskra，避碰性能、解锁性能和运输效率平均提升11.18%、22.69%、8.16%.由图7～图9可以看出，由于TW-Dijskra 无法实时的规避路径冲突，缺少有效的AGV死锁解除方法，随着运输任务量的增加，当各节点的最优时间窗均被占用时，其避碰性能和解锁性能会显著下降，导致运输效率降低.

Ant-agent-2hf和Ant-agent-hf在实现动态路径搜索的基础上，均可利用拥挤度阈值和冲突解决机制，实时避免AGV 间的路径冲突，结合AGV 的位置变化实时更新各节点处的拥挤度，并利用状态转移规则解除AGV 的局部死锁.但由于Antagent-2hf添加了启发函数F3，AGV可更加快速地接近目标点，在相同运输任务量下可减少AGV 路径冲突和停车次数，避碰性能较Ant-agent-hf 平均提升6.42%.Ant-agent-2hf与Ant-agent-hf均利用状态转移规则解除AGV 的局部死锁，但更少的路径冲突和停车次数降低了AGV 局部死锁程度，因而Ant-agent-2hf 解锁性能更优，较Ant-agent-hf 平均提升1.06%.避碰性能和解锁性能的优势使Antagent-2hf 具有更高的运输效率，较Ant-agent-hf 平均提升了5.02%.结合图9可以看出，Ant-agent-2hf在较大的运输任务量下，运输效率优势更明显.

5 结 论

针对自动化码头存在的AGV 路径冲突和道路死锁问题，提出基于Ant-agent 的AGV 控制算法.与传统的动态路径规划方法相比，Ant-agent算法可根据路网内AGV 位置实时更新各节点的拥挤度，利用状态转移规则和冲突解决机制，有效地解决AGV的路径冲突和道路死锁问题，提高AGV的运输效率.随着船舶大型化趋势的日益明显，Ant-agent算法在较大的运输任务量下具有更好的应用意义.