高速公路收费站车道类型设置问题建模与求解

林培群，梁韫琦

(华南理工大学土木与交通学院，广州510640)

0 引 言

2019年起我国将逐步取消全国高速公路省界收费站，并加快推进电子不停车快捷收费的推广应用.许多收费站在高峰时期通过开设复式收费车道来缓解拥堵，但在车流量较低的时段，开放过多的收费通道或安排过多的收费员将造成窗口闲置、资源浪费的现象.新政推行的过程中，在不扩建收费站的情况上，如何设置多种收费方式的车道组合方案，将是收费站管理运营者需要着重考虑的问题.

高速公路收费站车道设置已成为国内外许多研究者关注的问题.Robert Neuhold 等[1]利用视频检测系统开发出一种车道分配优化算法，引导车辆到排队长度较短的区域，结果表明该算法可有效减少车辆行程时间及车道排队长度；Seongmoon Kim[2]通过构建基于M/G/1 排队过程的非线性整数规划模型求解最佳的动态车道配置方案，该模型中运营成本影响因素较少，灵活性不足；姬杨蓓蓓等[3]构建了建设运营成本与延误成本最小模型，该模型采用单路排队多路服务的M/M/N 系统描述收费站排队现象，但实际情况下，车辆在排队中自由选择通道的机会很小，因此该模型的适用性不足.

现有研究未能兼顾各收费形式的特点，故本文根据ETC、MTC及复式车道的服务特性，建立车道类型设置优化模型，并提出一种自然数编码的遗传算法用于模型求解.

1 收费站车道类型设置优化模型

1.1 模型建立

以收费站运营成本与用户延误成本之和最小为目标建立模型，建模所需参数及其定义如表1所示.

(1)收费站运营成本.

收费站MTC 车道运营成本由3 部分组成：设备运行成本、材料购置成本及人工成本[4].按每人每月工作22 d，每天工作8 h计算人工成本.ETC车道运营成本，即ETC 设备的运行成本.综上，MTC与ETC车道的运营成本分别为

收费站总运营成本为所有车道的运营成本之和，即

(2)用户延误成本.

延误成本是车辆因接受收费服务及排队等待而造成的时间损失费用.客车延误成本与客车载客数量及人均时间价值相关，本文以收入法[5]计算人均时间价值.某小时到达收费站的客车延误成本为

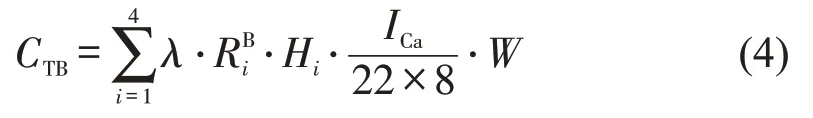
货车延误成本由单辆货车单小时的纯收益决定，某小时到达收费站的货车延误成本为

收费站的总用户延误成本为客车延误成本与货车延误成本之和，即

表1 参数及其定义Table1 Parameters and definitions

(3)用户延误时间.

车辆进入收费广场后，若广场内出现排队现象，车辆自由选择收费通道的机会很小，因此采用多路排队多路服务系统计算排队延误时间.一般假设车辆到达收费站服从泊松分布，到达收费站的车辆分为两种：已安装OBU 设备的车辆会随机进入ETC车道，其余车辆随机进入MTC车道(含复式车道).假设某小时到达收费站的车辆中，ETC车辆比例为θ，则收费站ETC车道的平均车辆到达率为

MTC车道的平均车辆到达率为

对于ETC 车道与1 窗口MTC 车道，各个车辆的服务时间相互独立(可将ETC 车道在高峰时期的最小车头时距视为其服务时间)，可认为其服从负指数分布服务[6].根据排队论[7]，可将每条车道视作一个M/M/1排队系统，其服务强度为

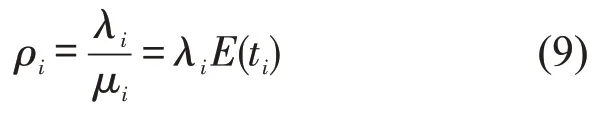
车辆在M/M/1排队系统中的平均排队延误时间(含服务时间)为

复式车道是多窗口同时进行收费的MTC 车道，复式车道服务时间包含车辆驶入收费通道就位时间与车辆在通道内逗留时间(受最长收费时间车辆影响)[7]，不能认为其服从负指数分布，故本文采用服务时间服从任意分布的M/G/1 排队模型来描述复式车道的排队过程，那么对于开启ni个窗口的复式车道，ni辆车同时接受收费服务，其服务强度为

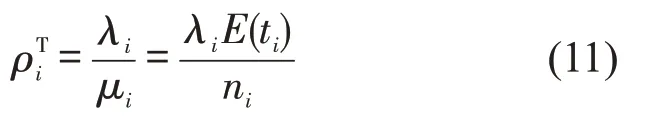
根据Pollaczek-Khinchin公式[8]，复式车道车辆的平均等待时间(不含服务时间)为

应用Little 定理[9]，车辆平均逗留时间应为平均服务时间E(ti)与平均等待时间WTq之和，但由于复式车道的服务时间中包含了车辆在通道内的行驶时间，在计算延误时应当将其减去，因此复式车道车辆的平均延误时间为

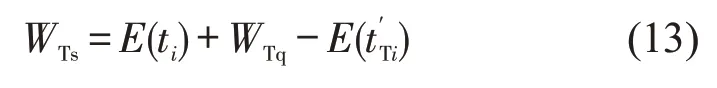
拥有N条收费车道的收费站，车辆因接受收费服务及排队等待造成的平均延误时间W为

各类成本、服务时间、车辆到达率、ETC 车辆比例，以及各类客、货车比例均为已知数，则总成本C可化为NE,NM的函数.为保证排队系统的稳定性，优化方案应使得每条车道的服务强度ρi ＜1.综上，得到模型的目标函数与约束条件为

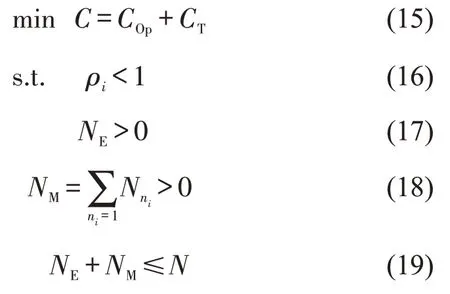
1.2 模型求解

收费站车道类型设置问题可视为决策由有限个独立子决策组成，每个子决策具有相同的离散型决策空间的组合优化问题，故采用一种基于自然数编码的遗传算法对模型进行求解.

如果决策问题具有m个独立子过程，每个子过程具有大小为n的公共决策空间，那么染色体可用1 个长度为m的一维数组来描述，该数组的每一位代表1个基因，可用1个n进制数来表示，m与n的取值范围为m∈ℕ+、n∈ℕ+(ℕ+代表正整数集)，一维数组每一位的取值空间为{0,1,…,n-1}，基于自然数编码的遗传算法流程如图1所示.

对于收费站车道类型设置问题，m为收费站单向已建成的车道总数量，n为收费车道的设置类型数，目标函数为收费站运营成本与用户延误时间成本之和C.考虑到此为一个最小化问题，适应度函数可描述为

式中：c(k,j)代表第k代的第j个染色体，隐含了NE,NM的信息；f[c(k,j)]为适应度函数；g[c(k,j)]为目标函数；gmax为输入值，应大于理论上总成本的最大值.

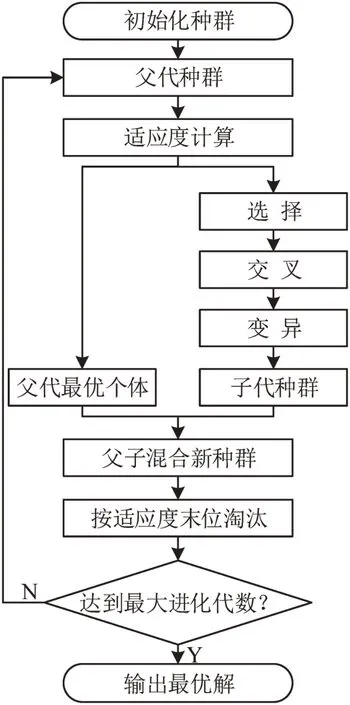
图1 自然数编码遗传算法流程图Fig.1 Natural number encoding genetic algorithm flow chart

2 实例分析

2.1 参数调查估计

选取广州市机场收费站作为研究对象，该收费站出口方向共15 条车道，其中，ETC 车道3 条，MTC车道12条.

通过现场调查，得到机场收费站出口方向服务时间相关参数如表2所示，通常情况下复式车道窗口数不超过3 个，其服务时间参数根据文献[7]所述方法使用Python编程进行模拟，模拟条件为：收费窗口间隔为9 m，排队车辆车头间距为7 m，车辆启动反应时间为1.5 s，通道内车辆平均行驶速度为8 km/h.成本相关参数如表3所示，各类客车平均载客量如表4所示.本文以车流量相对较大的2017年9月1日的广东省高速公路收费流水数据为基础，分析当日机场收费站出口方向的车流组成，具体结果如表5所示.

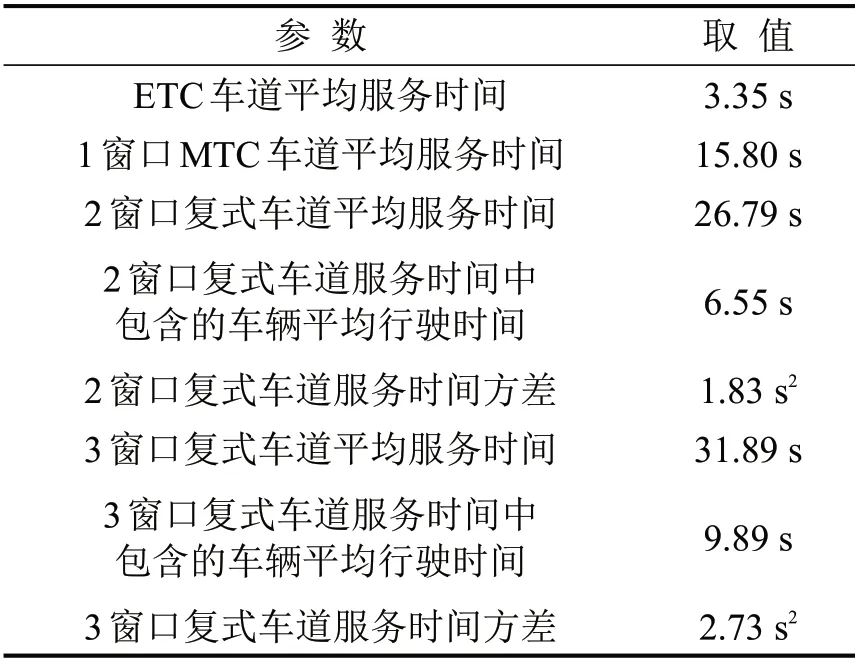
表2 服务时间相关参数Table2 Service time related parameters

表3 成本相关参数Table3 Cost related parameters

表4 客车平均载客量Table4 Average capacity of bus

2.2 优化方案求解与仿真

由表5可知，当日早高峰为[08：00,09：00)，以此为研究对象.将2.1 节中各项参数代入1.1 节所述模型中，求解得到优化方案1.根据我国关于ETC应用服务的发展目标——到2019年12月底，高速公路不停车快捷收费率达到90%以上，假设其他参数不变，将ETC 车辆比例输入为0.9，求解得到优化方案2，原始方案、优化方案及相关指标如表6所示.

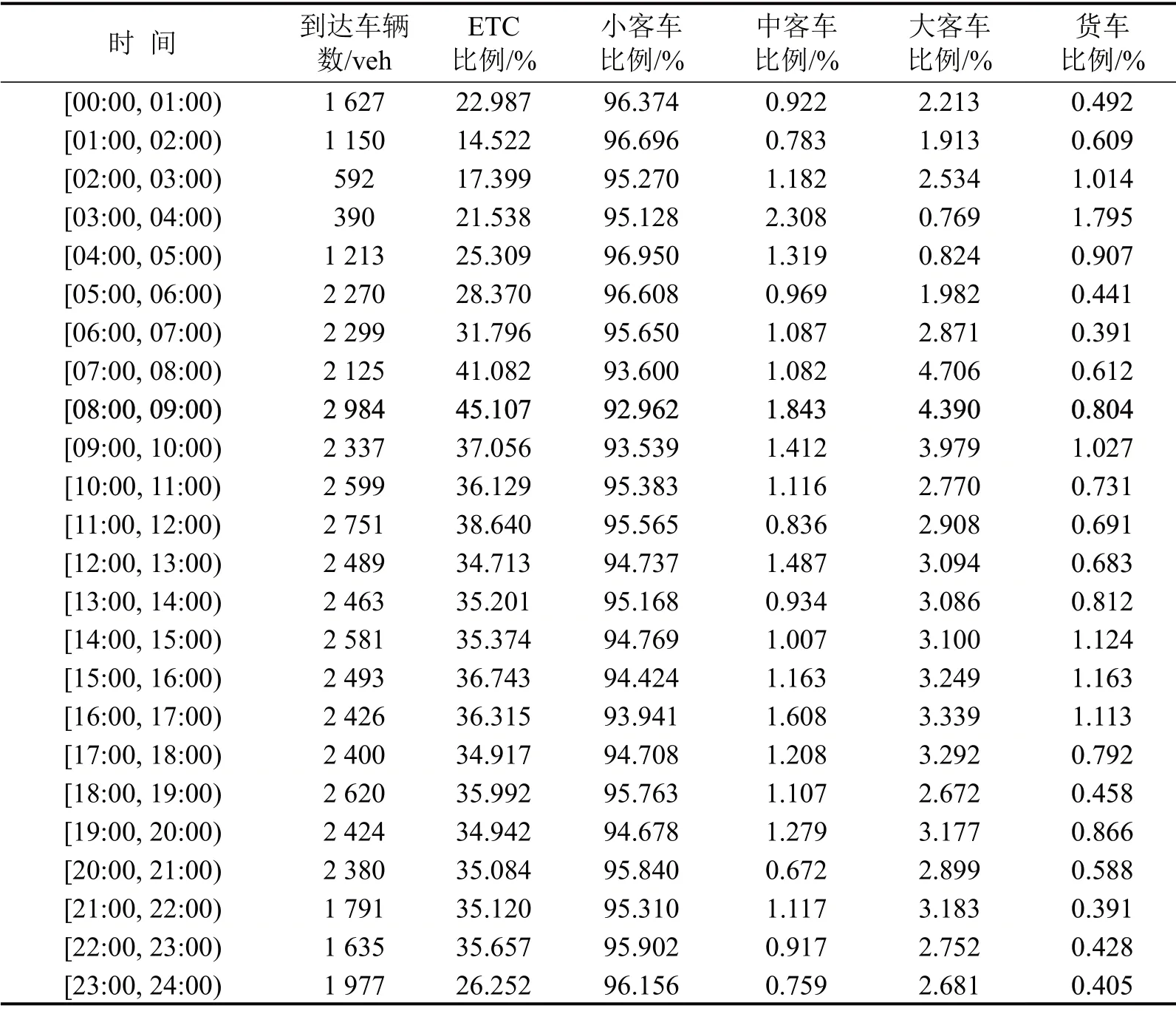
表5 机场收费站出口方向车流组成Table5 Composition of traffic flow at exit of airport toll station

表6 车道类型设置方案及相关指标Table6 Lane type setting programs and related parameters

采用自然数编码的遗传算法进行方案优化时，设置种群数量为80，交叉概率为0.4，变异概率为0.02，最大进化代数为300.进化代数—每代最小总成本曲线如图2所示，图中实线代表各代最小总成本，虚线代表理论最优解.优化方案1 的最优解首先出现在第213 代，求解时间为1.047 s，如图2(a)所示；优化方案2的最优解首先出现在第81代，求解时间为1.062 s，如图2(b)所示.

图2 进化代数—每代最小总成本曲线Fig.2 Evolutionary generations-minimum total cost per generation

以机场收费站实际几何设计为参考，使用VISSIM 4.3软件对3套方案进行仿真评价，仿真效果如图3所示.仿真相关参数设置如下：仿真时间为3 600 s，收费车道宽度均为3.5 m，长度为80 m，设置在收费广场出入口的行程时间检测器的直线距离为570 m，人工收费窗口及排队计数器设置在收费车道的50 m 处，车辆通过ETC 车道时无需停车，车辆通过MTC 车道时在收费窗口停车，停车时间采用期望为15.8 s 的指数分布.由于VISSIM 4.3 软件无法实现复式车道收费过程的仿真，故将复式车道简化为具有相同通行能力的1 窗口MTC车道.3套方案的仿真结果如表7所示.由表7可知：优化方案1 降低了MTC 车辆的平均延误，停车次数及排队长度；优化方案2 中ETC 车辆占绝大多数，收费站整体通行效率的提升更加明显.3 套方案的仿真评价结果与模型计算结果基本一致，故本文提出的收费站车道类型设置优化模型具备可靠性.

图3 收费站仿真效果图Fig.3 Toll station simulation schematic diagram

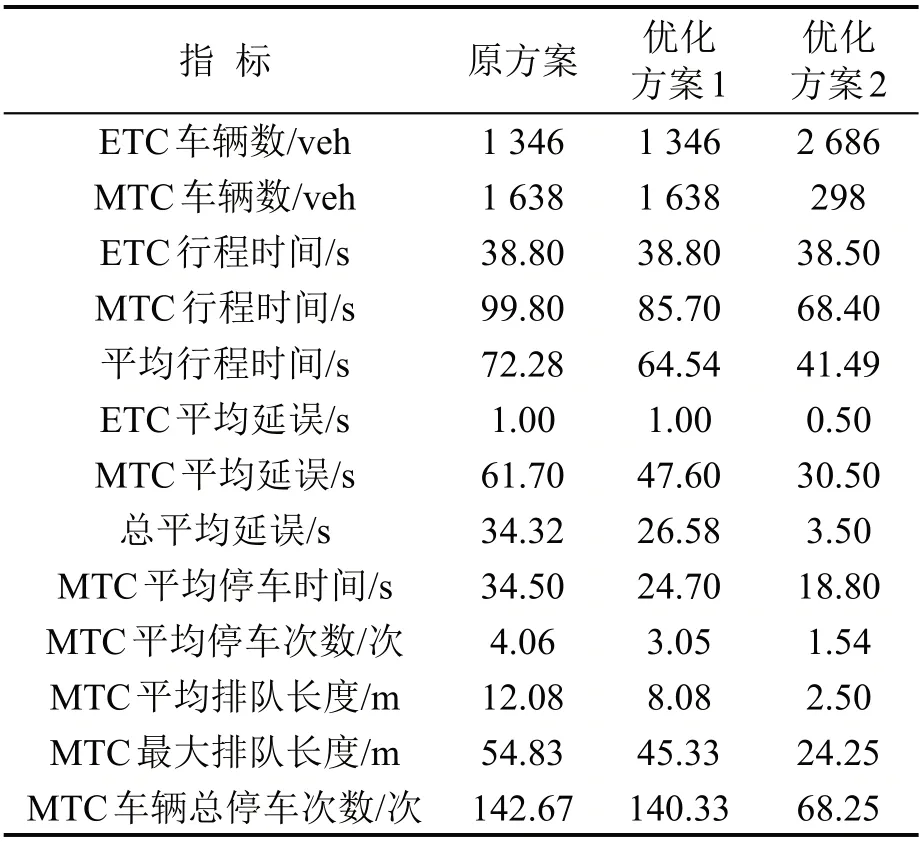
表7 仿真评价指标Table7 Simulation evaluation indicators

由表5可知，05：00-21：00每小时收费站出口方向驶出的车辆数均维持在2 000 veh 以上，夜间逐步减少，可见机场收费站出口方向的车辆到达率与机场航班的出发时间密切相关.利用车道类型设置模型求解全天的最优车道配置方案，如图4所示，图中MTC_1、MTC_2、MTC_3 分别代表开启1、2、3 个收费窗口的MTC 车道.由图4可知：当日05：00-21：00中有14 h均设置了12条2窗口复式车道，3条ETC车道，可见日间车道设置方案变化不大；而夜间车流量较少时，不再使用复式车道，开启的总车道数逐步减少.在实际工作中，可将05：00和21：00作为日夜班的切换节点，方便收费员排班.

2.3 灵敏度分析

由表5可知，机场收费站出口方向车流中绝大部分为小型客车，比例稳定在95%左右，其他车型车辆比例虽有波动，但比例较小，对车道配置方案的影响不大.假定小、中、大型客车及货车的比例分别为95%、1%、3%、1%，得出不同到达率与ETC比例下的最优车道配置方案如图5所示.由图5可知：在ETC比例一定时，开启车道的总数量会随着到达率的增加而增加，复式车道的数量也会随着到达率的增加而增加；在到达率一定时，开启车道的总数量会随着ETC 比例的增加而减少，ETC 车道的数量会随着ETC 比例的增加而增加.由于MTC 车辆的延误时间明显高于ETC 车辆，并且每小时的用户延误成本相对大于收费站运营成本，因此总成本这一目标函数的最主要影响因素是MTC车辆的小时到达率，那么通过减少使用MTC的用户数量，能有效地降低总成本.

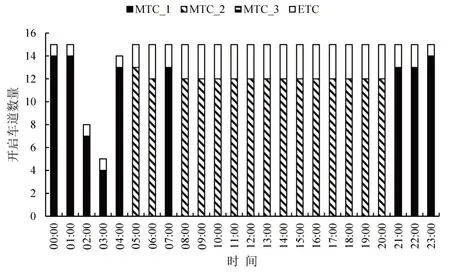
图4 全天车道类型设置方案图Fig.4 All-day lane type setting scheme

图5 不同到达率和ETC 比例下的设置方案图Fig.5 Setting scheme under different arrival rate and ETC rate

3 结 论

本文以收费站运营成本与用户延误成本两者之和最小为目标，结合多种收费方式，建立收费站车道类型设置优化模型；针对模型求解，提出一种自然数编码的遗传算法，该算法对求解离散型决策空间的组合优化问题具有通用性；以广州市机场收费站为例，求解高峰时段不同ETC 使用率下的两种优化方案并进行仿真对比，讨论了不同到达率与ETC 使用率下的合理车道组合方案.结果表明，所提方法能有效地缓解收费站的排队现象并减少资源浪费.收费公路制度改革虽然会产生诸多问题，但从长远来看，就交通系统本身而言，加快推进ETC 应用服务将对缓解收费站拥堵，节约运营成本起到十分积极的作用.