考虑人口效益的城市路网OD矩阵推算模型

裴玉龙，高 维

(东北林业大学交通研究中心，哈尔滨150036)

0 引 言

研究交通分布是理解人类运动宏观规律，探究城市未来发展形态的重要手段.为了探究不同空间尺度上交通分布对人口空间移动的描述程度，Zipf 首次将重力模型应用于交通领域.重力模型经过一个多世纪的发展已经成为交通工程师开展交通预测的主要方法，但重力模型存在待定参数使其无法摆脱对大量调查数据的依赖.因此，一些没有可调参数的预测模型被构建出来，如Simini等[1]提出的辐射模型和闫小勇等[2]提出的人口加权机会(PWO)模型.辐射模型和PWO 模型均假设人口分布来决定交通分布[3].然而，这种单一变量的假设与实际情况不符，忽略了人口流动的复杂性，不能精准地描述城市路网交通分布[4].本文通过对广州市海珠区基础交通数据的分析，探讨城市道路交通分布的可预测性，提出了靶向双联模型，以期在保证传统重力模型精度的前提下，提高预测效率、降低工程实践中的预测成本.

1 传统的OD推算模型

1.1 重力模型

19 世纪中叶，Zipf 和Stewar 首次将重力模型应用于交通领域，通过铁路运输量、电话通话量等城市间的基础数据研究两个城市空间的相互作用，并构建了重力模型基本形式.Zipf 通过大量的实验发现，两个城市间的这种比率在双对数坐标系上呈线性分布.这一结论在交通领域得到了广泛的应用和发展，许多学者针对重力模型在实践中存在的不足，提出了多种不同的扩展形式，较有代表性的是双约束重力模型，即

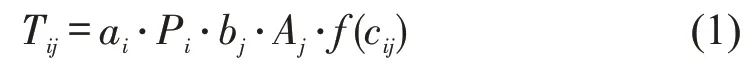
式中：Tij为从i到j的交通流；Pi和Aj分别为i的交通生成量和j的交通吸引量；f(cij)为阻抗函数；ai，bj为两个平衡因子，计算公式为

模型假设交通区域之间的交通流量与交通区域(原点)的生产力和交通区域(目的地)的吸引力成正比，并且随着它们之间的交通阻抗衰减.尽管重力模型为了适应不同条件下的工程需要发展出了多种拓展形式，但它并不是基于牛顿引力定律的一个松散类比的特设模型，一个特定的“重力”模型，实际上是给定的可用已知信息OD流量的最小偏倚，统计上最可能的预测值.

1.2 辐射模型

辐射模型是近年来继重力模型之后，另一个被学术界广泛认可的预测模型[1].它突破了传统重力模型含有待定参数的限制，通过输入人口分布数据来预测交通分布.模型假设每个地点的就业机会数量与居住人口成正比，并且出行个体选择距离家最近的工作地点而非利益最大的工作地点.当选择目的地为j时，从出发点i到j的平均交通量Tij为

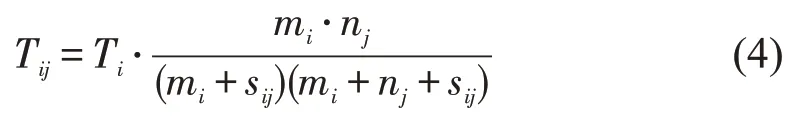
式中：Ti为i的发生量，；mi和nj分别为i和j的人口；sij为以i为圆心rij为半径范围内的总人口，但不包括出发点人口mi和目的地人口nj.

重力模型在预测之前需要根据现状数据对待定参数进行标定，需要通过高成本的人工调查来实现，极大地限制了重力模型的构建频率.一些地区为了节约成本，尽可能地减少调查次数，不断延长现状路网OD矩阵的有效期，这严重影响了交通工程师对路网流量分布的判断.辐射模型解决了这一问题，在宏观层面预测效果较好，但实践发现，辐射模型由于变量单一，无法满足城市道路复杂多变的交通分布预测.

2 多因素加权的OD推算模型

2.1 人口加权机会模型

人口加权机会模型(PWO模型)的假设前提与辐射模型相似，认为个体在选择目的地之前，将权衡每个地点机会的大小.尽管一个位置的机会很难直接测量，但它的数量可以用与人口的比例关系反映出来[2].因此，PWO 模型认为个体出行的讫点(目的地)并非是选择距离起点(出发地)最近的地点，而是选择机会相对较多的地点.

为实现使用“出行机会”代替“出行距离最短”来刻画个体出行轨迹，引入了机会模型，即

式中：Aj是讫点j相对于出行个体在起点i的吸引量，以用来表征吸引能力强弱；oj为讫点j和以讫点j为圆心Sji为半径的总人口在城市中的总机会(包括起讫点人口)；Sji为起讫点之间的距离；M为讫点的人口，1/M为有限大小校正.

与辐射模型类似地，假设从i到j的出行概率与j的吸引力成正比；个体出行机会数量oj与讫点的人口成正比，我们可得到PWO模型为

式中：N是交通区总数；k为交通区编号；mk是交通区编号为k的人口；Ski是以k为圆心rki为半径范围内的总人口.

PWO模型相较于辐射模型在城市范围内具有更高的预测精度，主要是辐射模型的假设限制了个体出行选择更远的位置.无可调参数的模型尽管优势明显，但从模型的假设条件可以发现，辐射模型和PWO 模型都无法描述环境变量对个体行为的影响.预测精度会受到实际条件制约，无法与重力模型相比.

2.2 靶向双联模型

2.2.1 城市路网OD矩阵统计规律

PWO 模型有效避免了重力模型前期大量的OD调查，弥补了辐射模型在城市尺度范围内出行距离衰减过快的问题.辐射模型和PWO模型只考虑人口因素虽然可以成功预测居民出行轨迹，但预测效果过于宏观.为了探究城市道路交通分布的统计规律，将广州市海珠区现状道路根据道路技术等级划分为高速公路、快速路、主干路、次干路，并绘制现状路网[5]，如图1所示.海珠区属于广州市中心城区，北临越秀区、天河区，西接荔湾区，南临番禺区；西部和北部主要以居住用地为主，东南部是瀛洲生态公园，辅以部分居住用地.

图1 广州市海珠区道路网Fig.1 Urban road network of Haizhu District,Guangzhou

海珠区骨架路网是由一条东西向主干路及多条南北向快速路组成.现已形成“一区两片、四心三轴”的城市空间结构.根据城市空间布局、自然地理条件及现状路网结构将其划分成142 个交通小区.通过海珠区道路基础数据及路网OD矩阵构建交通分布模型，如图2所示.

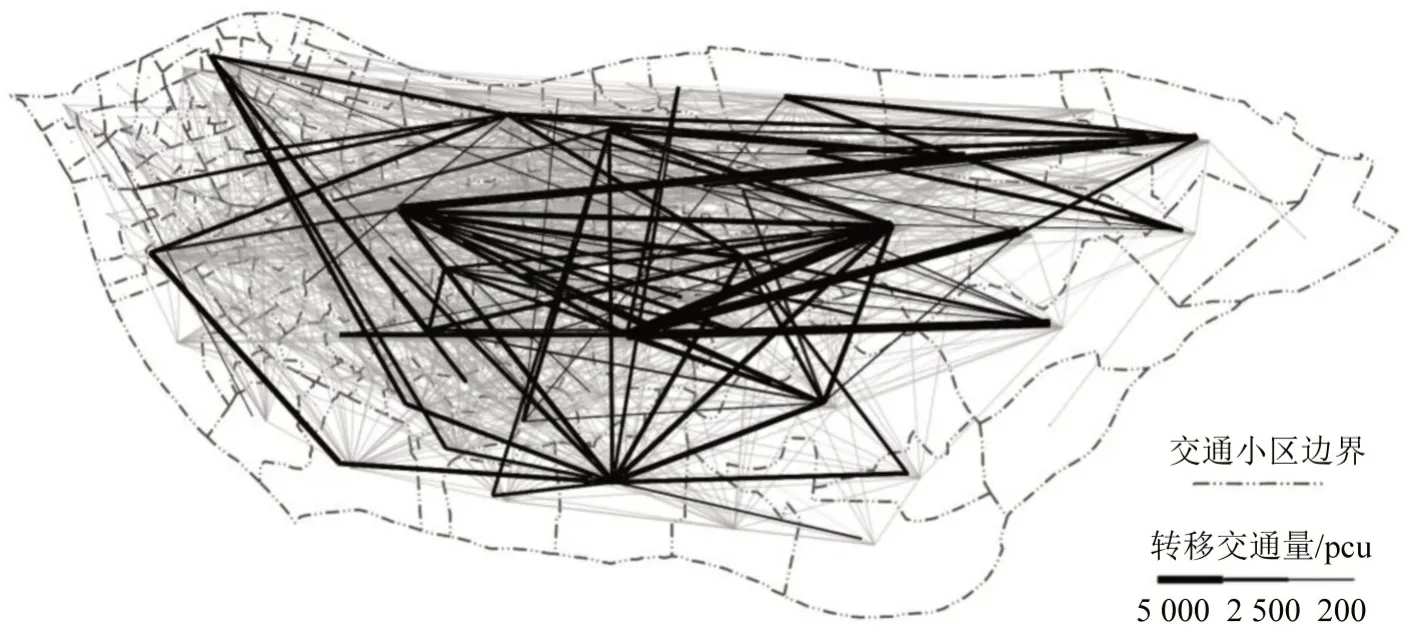
图2 海珠交通分区及交通分布Fig.2 Traffic zoning and traffic distribution in Haizhu District,Guangzhou

为了分析交通流特征，图3给出了142个交通区之间交通流的概率分布.为更直观的探究其中的规律，将相近区间值的交通量概率累加，简化了散点的特征形态.这是一种典型的长尾分布，由幂律函数和指数拟合.结果表明，年平均日交通量在105～533 pcu 之间变化较大，平均值较低.为了进一步研究每个交通小区的发生量是否具有交通流分布同样的特征，在图3的插图中绘制了142个交通小区发生量的概率分布.结果表明，每个交通小区的发生量也遵循幂律分布，说明城市路网中交通流的转移与交通小区的发生量均具有高度的异质性，遵循Zipf 定律.此外，城市人口分布和城市经济规模分布同样存在相类似的特征[6].因此，交通流的分布特征很可能与城市人口和经济规模分布有关，在理论上验证了模型的假设条件.

图3 交通区之间交通流概率分布Fig.3 Probability distribution of traffic flow between traffic zones

为了进一步探究交通流分布特征与人口、经济规模分布的内在联系，对交通区的人口、经济及发生量等指标进行了多元非线性回归分析，其中R2约为0.87，R2adjust约为0.86，说明交通流分布特征受当地人口和经济规模影响较大且自变量的增加未对R2结果造成显著影响，拟合结果如图4所示.在图5中显示了142 个交通区的残差分析结果，其中仅有5 个异常值，异常点个数为样本总量的9%，表明该模型对发生量的拟合有效.

2.2.2 模型构建

综合分析上述统计规律，居民出行不会因为距离远或行程时间长而显著减少，表现出一定的靶向强制性及时间不均匀性.说明辐射模型提出的个体优先选择最近可替代目的地出行的假设条件过于简单，但也不同于PWO模型提出的用人口表征机会来选择出行地点.因此，在借鉴PWO 模型优化辐射模型在城市尺度范围内出行距离衰减过快的基础上，提出了靶向双联模型(简称为TDM模型).模型假设出行个体在选择目的地时，会优先选择目的地生产力水平高和人口集聚效应显著的地点出行.如城市居民每天主要以通勤、餐饮、娱乐购物为主要出行目的，城市的商业、办公、科教文卫用地往往是一天内人口流动最大的地块.为了描述城市人口的这种空间移动规律，提出了靶向聚类系数，即

式中：Cj是靶向聚类系数，表征讫点j集聚人口的能力，Cj越大集聚能力越强；Pj为讫点j的人口；Gj是讫点j的经济水平，可用地区生产总值计算.

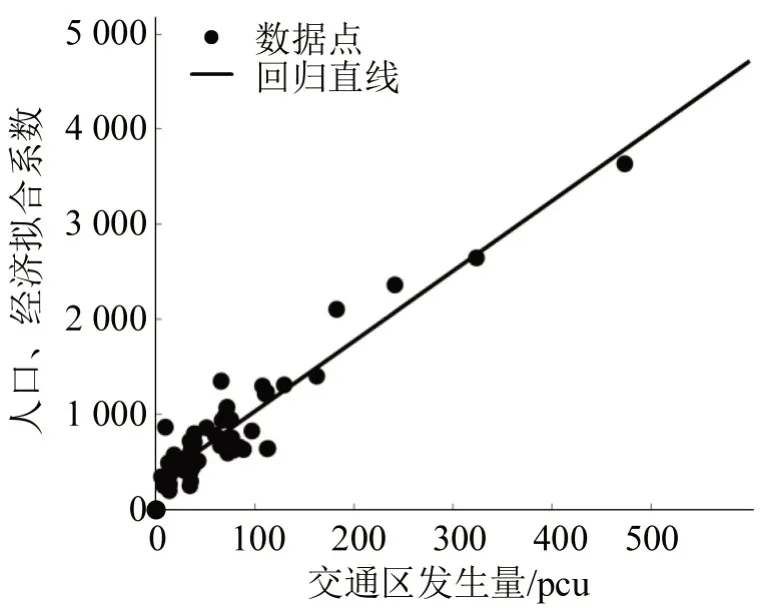
图4 发生量与经济、人口拟合优度Fig.4 Goodness of fit between production and economy and population

图5 发生量与经济、人口指标残差分析Fig.5 Residual analysis of production and economic and population

我们假设讫点j对居民出行的集聚能力与讫点j的靶向聚类系数成正比，那么从起点i到讫点j的居民出行轨迹可以用TDM模型表示为

式中：Tij是从i到j的交通流；Ti是i的发生量，是i和j的人口之和；M是城市中的总人口；k为交通区编号；N是交通区总数；Pk和Gk分别是交通区k的人口和经济水平；wki为编号为k的交通区和交通区i的人口之和.

为了验证模型的有效性，将现状OD矩阵生成P、A列并用靶向双联模型推算OD分布.实验过程隐藏了模型中200 pcu以下的数据，以便于观察分布特征.推算结果如图6(d)所示，为了比较与既有模型的推算效果，分别使用重力模型、辐射模型及PWO模型重复了上述过程，如图6(a)～(c)所示.

图6 4 种模型OD 分布结果Fig.6 OD distribution results of four models

重力模型对真实数据分布情况的描述最为接近，推算误差最小，其次是TDM模型.PWO模型有效弥补了辐射模型出行量随出行距离增加衰减过快的问题，但推算误差仍然显著.辐射模型在分布图中暴露出了自身缺陷，在交通区划分密集的西部地区拟合效果明显好于东部地区.这是由于东部地区受城市空间布局、自然地理条件及现状路网结构等因素影响，划分交通区较大，交通区之间的型心距较长.为了比较推算模型的准确性，我们将推算值与实际值的相对误差定义为

式中：是从i到j的推算交通量；Tij为从i到j的实际交通量.Rij＞0 和Rij＜0 分别表示预测值高于实际值和预测值低于实际值.当Rij出现±∞时采用绝对误差，否则采用相对误差.根据Rij值，预测精度分为4个等级：准确(A)、相对准确(B)、相对不准确(C)和不准确(D)，如表1所示.

表1 推测结果的准确度等级Table1 Grade of accuracy of predicted results

通过上述方法比较4种模型精度，如图7所示.在预测等级(A)方面，重力模型最高(58%)，TDM模型次之(54%)，PWO 模型和辐射模型较低(均不足50%)；预测等级(D)，辐射模型最高(32%)，其次是PWO 模型(28%)，重力模型和TDM 模型相对较低.预测等级(A)，TDM 模型非常接近重力模型，目前工程实践中广泛采用重力模型进行交通分布预测，TDM 模型可以达到工程精度要求.TDM 模型仅使用交通区人口和经济指标即可推算分布矩阵，不需要现状OD 矩阵参数标定.由此可以得出结论，TDM 模型在工程实用性上高于其他3 种模型，也更适合预测城市交通分布.

图7 4种模型精度分布Fig.7 Accuracy distribution of four models

3 模型应用

根据深圳市城市空间布局、自然地理条件及现状路网结构，将其划分为542 个交通小区，已获取相应的现状OD矩阵，结合深圳市城市路网建立交通分布模型.为了便于观察分布特征，实验过程隐藏了模型中100 pcu以下的数据，如图8所示.

图8 深圳市交通分区及交通分布Fig.8 Traffic zoning and traffic distribution in Shenzhen

根据已知的交通区发生量与吸引量分别使用重力模型与TDM模型对深圳市542个交通小区进行OD矩阵推算，结果如图9所示.

从图9可以明显看出，重力模型与辐射模型均在城市南部推算出大量转移的交通量，这符合深圳市现状客流的分布特点.东部地区不论是发生量还是吸引量均较低，这是由于东部地区远离城市中心且具有较大面积的山地林地，城市路网密度相对不高，骨架路网以公路为主，并未完全包括在模型范围内.

为了验证推算模型的准确性，我们分别计算了重力模型和TDM模型相对于现状OD分布的准确度等级，其结果如图10所示.

从图10可以看出，重力模型的准确度等级仍略高于TDM 模型，但相差并不悬殊.在预测等级(A)方面，两者相差6%，综合考虑预测等级(A)和预测等级(B)，两者相差2%.由此可以认定，TDM模型可以较好地描述城市空间尺度范围内的人类移动.

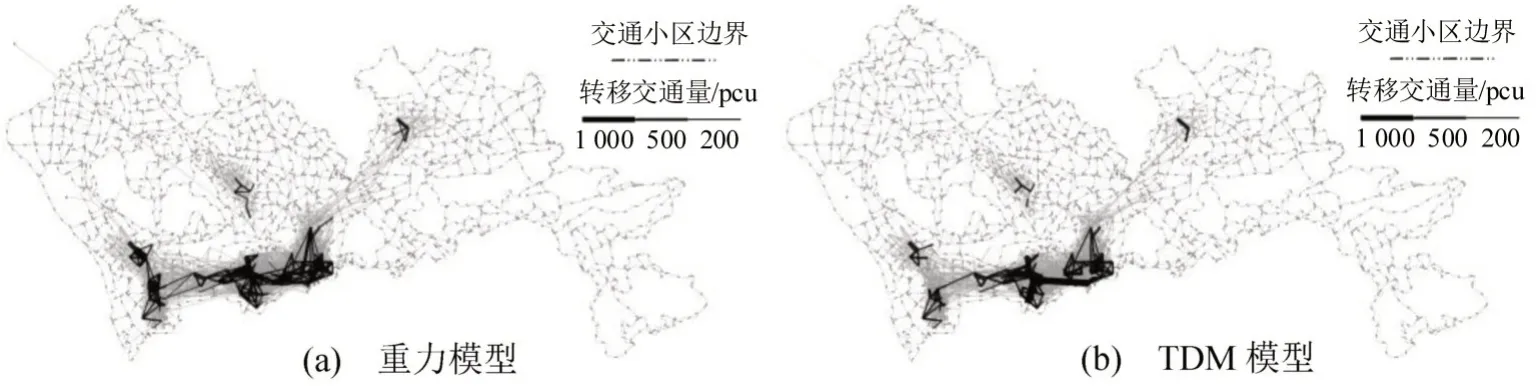
图9 两种模型OD 分布结果Fig.9 OD distribution results of two models

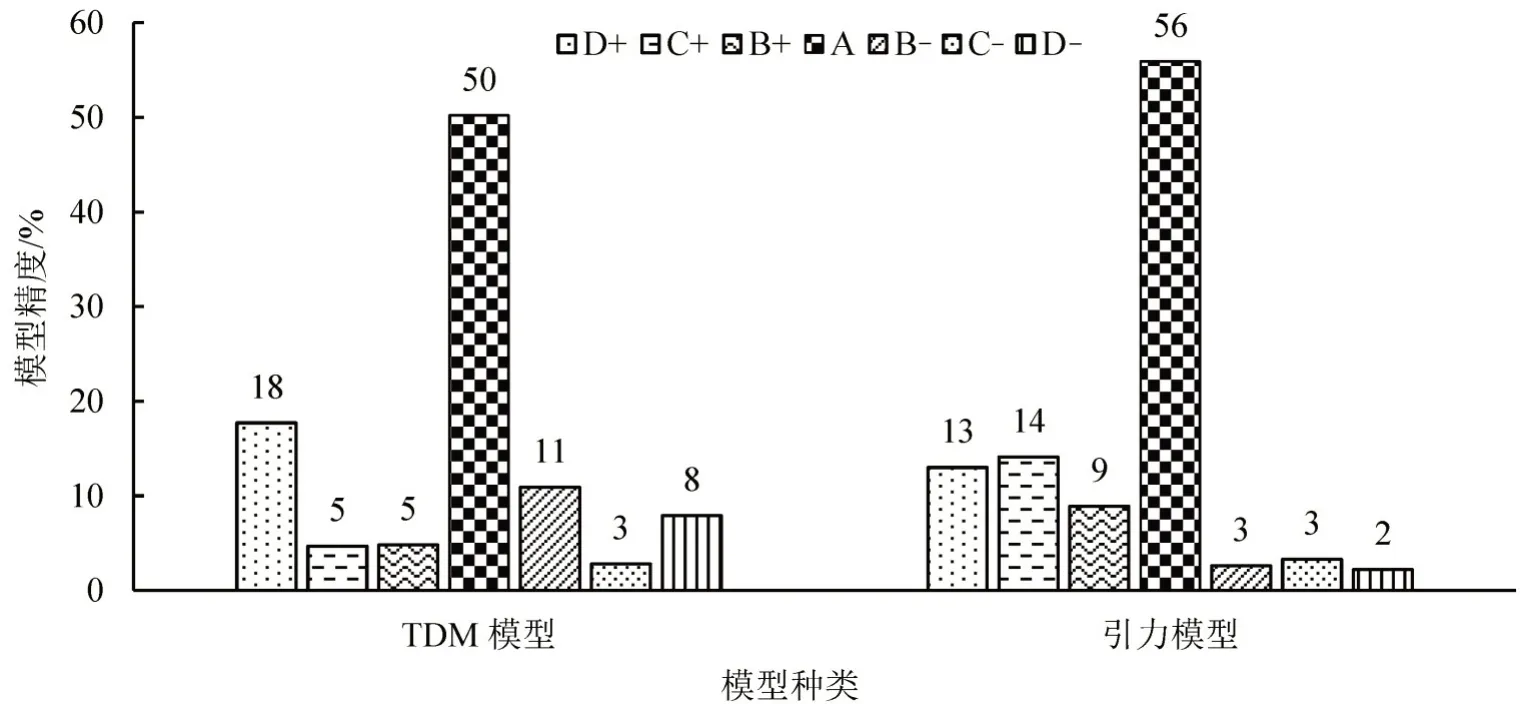
图10 两种模型精度分布Fig.10 Accuracy distribution of two models

4 结 论

本文通过对广州市海珠区城市道路交通分布基础数据的清洗和分析，建立了城市道路交通分布模型并对城市道路交通分布的统计规律和可预测性进行研究，得到结论如下：描述3种既有的OD矩阵推算模型，给出交通区之间交通流的概率分布及各个交通区发生量的概率分布，两种分布表现出高度的异质性，并遵循Zipf定律；通过交通基础数据分析发现交通区发生量与人口、经济规模具有类似的幂率分布规律，通过多元非线性回归分析及残差分析确定了发生量与人口、经济规模的数量关系；提出一种考虑人口效益的靶向双联模型(简称为TDM 模型)，根据确定的相对误差和绝对误差，将推算模型的预测精度划分为4 个等级，结果表明，TDM模型具有较高的预测精度并在预测成本和效率上，优于其他3 种模型，更适合预测城市交通分布.