基于LSTM神经网络的降雨天旅行时间预测研究

王志建，李达标，崔 夏

(北方工业大学北京市城市道路交通智能控制技术重点实验室，北京100144)

0 引 言

日渐拥堵的城市道路给人们出行带来了巨大的困扰，正确地选择一条合适的出行路径会给出行者节约不少成本.路径的选择取决于该路线的行程时间和在该时间内顺利到达目的地的可靠性.出行天气的不同会对行程时间产生较大影响，在降雨天气下高德地图对易拥堵路段进行了标定，方便出行者更好地选择出行方式和路径.国内外不少学者在降雨的背景下对城市道路运行状态和行程时间的计算和预测展开了大量的研究.许方经[1]结合降雨对城市道路通行能力和道路网可靠性进行了分析；姜桂艳[2]等用传统的数学模型和支持向量机对行程时间进行预测分析；丁宏飞[3]等采用了基于神经网络的BP 算法计算行程时间并取得了一定的成果；DUAN Y.J.[4]，Siripanpornchana[5]等采用不同的神经网络算法对行程时间预测做了大量的研究分析.综上，计算行程时间的研究方法主要集中在数学理论模型和神经网络.传统的数学理论模型有较差的可移植性.前馈神经网络在学习速度上较慢且容易陷入局部最优，而支持向量机更适合小样本下的计算.

本文对轨迹数据进行分析和预处理，把车辆轨迹划分成若干条由最小路段组成的子路径.把轨迹数据和降雨数据作为模型的输入，通过LSTM神经网络对每条子路径做行程时间的预测，最后把所有子路径的行程时间求和得到最终的行程时间.同时与应用较广的算法Kalman、BP 神经网络和SVM 方法进行对比分析.结果表明，本文算法在行程时间预测上有较高的准确性和可靠性.

1 数据准备

1.1 数据预处理

本文数据为中关村西区2018年7月1～7，10，17和24日，共10 d经处理后的1 500万余条轨迹数据.采集设备每12 s 上传一条定位及车辆行驶状态，数据集包含字段信息：CreateData、CreateTime、CarID、Longitude、Latitude、Velocity等.为提高数据的利用率，需要对原始数据进行除冗处理.删除GPS 状态为0、速度异常、同一时刻重复记录的数据，以及经纬度超出地图研究范围和相邻定位点存在较大偏移的数据.

研究路网范围为中关村西区，经度为东经116.273 2°～116.342 0°，纬度为北纬39.959 6°～39.996 2°.未打断路网道路前该区域共计1 284 条道路，存在不同道路相交的节点处进行打断处理，分析其拓扑结构[6].打断后路网数据集包含了4 686条路段和2 769个节点元素.打断后的部分路网如图1所示.

1.2 节点时刻及路段平均速度计算

地图匹配完毕后，得到每辆车的行驶轨迹GIS数据，接下来计算浮动车经过每个节点(交叉口)的时刻，由于轨迹数据采样时间间隔为12 s，按照城市道路一般行驶速度标准在一个采样周期内大概可以行驶130 m 左右.为方便计算通过节点的时刻，采用下面的方法进行计算：

(1)一个采样周期内仅出现一个节点.

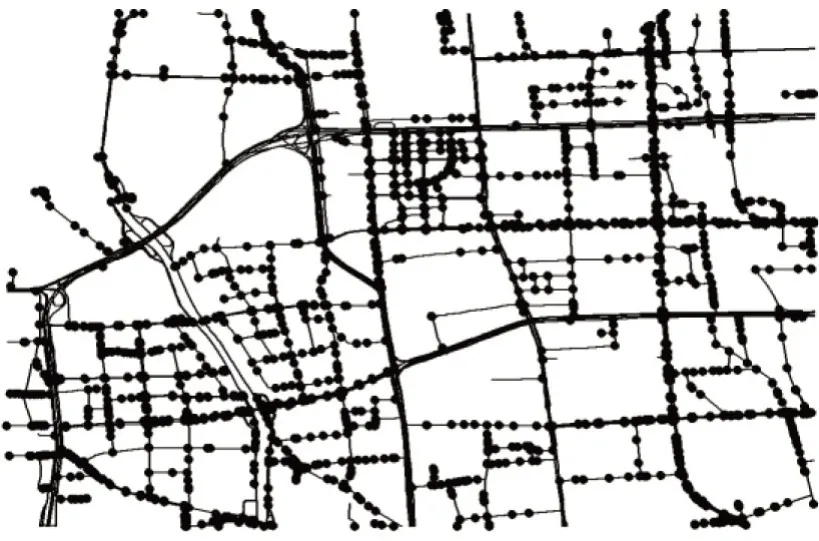
图1 路网局部拓扑Fig.1 Local topology of road network

图2中，Sn表示路段编号，Pn表示定位点，dn与dn+1表示定位点与节点之间的距离.

图2 一个周期内只有一个节点Fig.2 Only one node in a cycle

当pn点速度为0时，考虑可能在等待红灯，所以车辆经过节点N时的时间计算为

当pn点速度不为0 时，节点N的时刻可由前定位或后定位点获取.

式中：N车辆经过节点，Tn为车辆经过节点N的时刻；dn和dn+1为两个定位点距离节点的距离；tn和tn+1分别为相邻两点的定位时间；vn,n+1为相邻两点间的平均速度.

(2)一个采样周期内存在两个及两个以上节点.

图3中，N,N+j表示路段节点，j=1,2,3,…,n,经过途中任意节点的时间为

式中：Tn+i为车辆经过相邻两个定位点间某一个节点的时刻；dn+i为节点到定位点的距离.

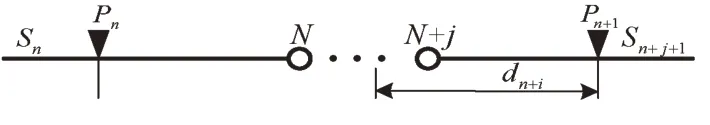
图3 一个周期内有多个节点Fig.3 Multiple nodes in a cycle

计算行驶距离时会出现路段为非直线型和直线型路段，为方便计算定位点到节点的距离，采用混合距离计算方法.距离计算分为为两部分：

①道路线型类似于直线时，可根据经纬度信息直接计算其欧式距离为

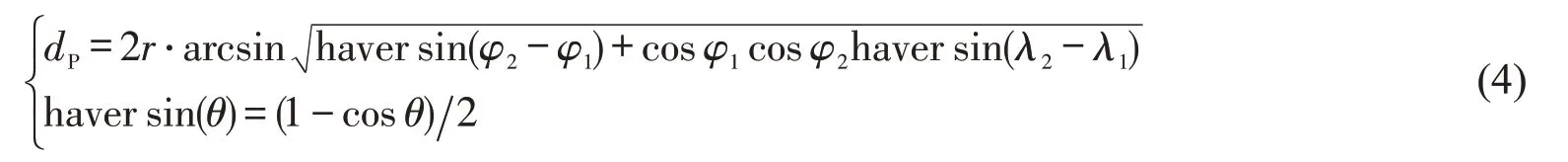
式中：r是地球半径；φ1和φ2是点1 和点2 的纬度；λ1和λ2是点1和点2的经度.

②当路段成非直线时，采用速度—积分模型估计车辆行驶距离，即

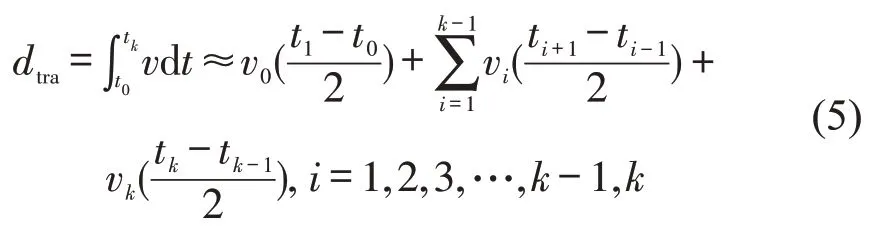
已知车辆在时间段内行驶的距离，可求的车辆在子路段里的平均速度为

式中：为最小路段平均车速；va为子路径平均车速.

完成地图匹配和节点时刻、平均速度计算后，将原始的GPS轨迹数据转换成基于路段ID的轨迹信息表，数据表包含4条属性，分别为：车辆ID、路段ID、路段末端节点时刻和路段平均行驶速度.

2 路径行程时间计算方法

现有的研究方案中，通常将整个行驶路径划分为最小路段进行旅行时间计算.在求解的过程中将最小路段行驶时间和交叉口损失时间相加，这样计算固然简单，但是因为交叉口损失时间的不确定性，使得计算结果存在较大误差.本文以行驶轨迹数据和GIS地图数据支撑，对数据进行分析利用数据流向如图4所示.

在已知出行起点及终点的情况下，以最短路径或最优路径为条件选择路径的基础上，对每条路径进行行程时间的预测.S表示路径集合，每个元素是由道路名称首字母缩写和编号组成.假设某出行者的路径规划如图5所示.

图4 数据流向图Fig.4 Data flow diagram

图5 出行路径示意图Fig.5 Travel path diagram

图5中推荐的路径一共经过了7 条道路共计17个路段，可以表示为

本文计算行程时间不再是将每个最小路段的行程时间单独计算出来最后单纯相加，而是将路径S根据已存在的历史车辆行驶轨迹逐次匹配，将整条路径S分成若干子路径，子路径是由最小路段累加获得.匹配方法是把路径S对应的路段ID 序列起始点与基于路段ID 序列的每条历史轨迹进行匹配，记录能连续匹配上的路段数和轨迹的条数.计算每次匹配的权重确定最佳子路径.

匹配路径匹配算法：问题描述：已知路径S={x1,x2,…,xn}，历史轨迹数据库carID 为文件列表，以路径S 为参考依次与carID匹配，并记录匹配上的路段 ID 和数量.1：For(int i=1;i ＜=length(i);i=i+a)2： NuCar=Nu(CarID)3： For(int Nu=1;Nu＜=NuCar;Nu++)4： CarID=NuCar 5： String TraCar=CarID.line 6： Int a=1 7： For(int y=1;y ＜=length[TraCar]；y++)8： String StrID=l[i]9： If StrID==TraCar[y]10： StrID=l(i++)11： a++12： printf(‘打印出相同路段数a’)13： Else a=1 14： Return(0)15： Return(0)16：Return(0)

路段数量统计之后，确定第一次匹配的子路径，采用mapminmax[0,1]函数，对权值进行归一化分析.

式中：Y为归一化后的权重值；Xmax,Xmin为数列X的最大值和最小值；xi表示匹配连续路段的数；Ni表示在样本中连续路段数为xi的数量.最大Y值对应的子路径作为此次匹配结果，依次重复匹配直至路径L完全匹配成功，过程图如图6所示.

路径S可表示为子路径的集合，即

路径S组合之后，把每条子路径与基于路段ID 的历史轨迹进行匹配，获取起始时刻，子路径行程时间和子路径平均速度.此时的数据集并不是固定时间间隔的序列，为方便模型的训练和预测，对序列进行了时间间隔为5 min 的数据处理.时间戳精确到分钟，以5 的倍数存储.若5 min 间隔内存在多条数据，行程时间和平均速度为多条数据均值；若5 min 内无匹配数据的，取相邻前后两个5 min 数据的均值存储.具体的字段信息如表1所示.

图6 分段匹配流程Fig.6 Piecewise matching process

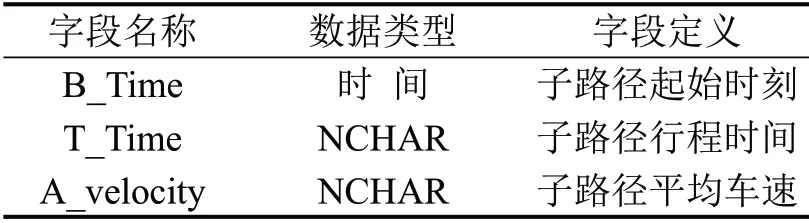
表1 子路径信息表Table1 Information of sub-path

总的行程时间为

式中：T为总的行程时间；ti表示通过LSTM 神经网络算法预测的每个子路径的行程时间.

3 建模和实例验证

近年来交通数据量的快速增长，导致传统的计算方法和数学模型不能满足对数据分析的要求，利用神经网络算法对大数据的分析得到了快速发展.部分学者采用LSTM 循环神经网络模型对行程时间的预测展开深入研究，该模型可以自动保存历史序列信息，有特殊的时间特性结构，对于行程时间预测有着良好的适应性.单个模型结构如图7所示.

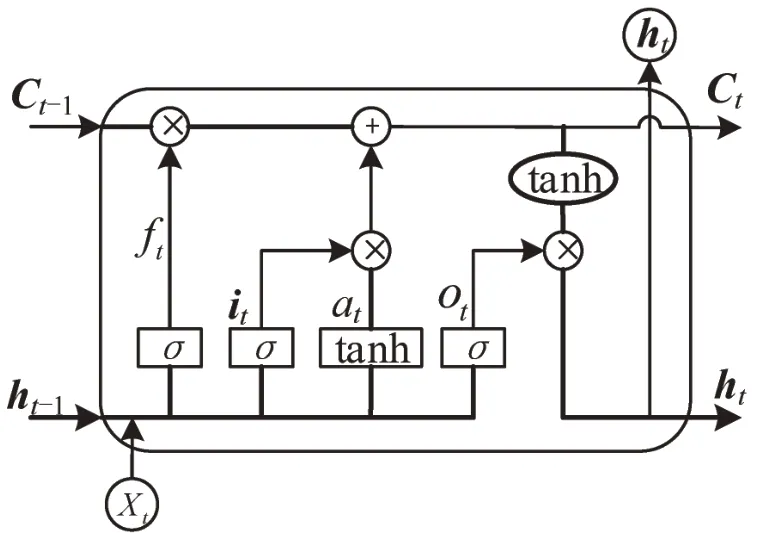
图7 单个LSTM 单元的内部结构Fig.7 Internal structure of a single LSTM unit

遗忘函数为

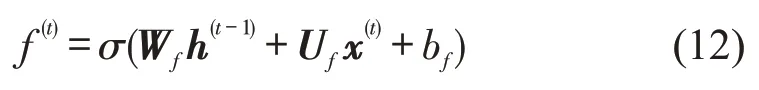
输入函数为

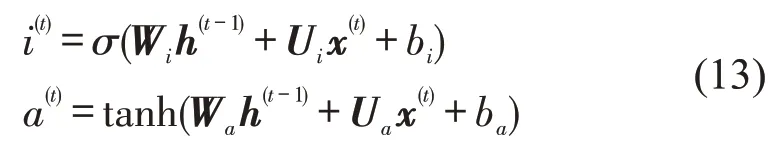
输出函数为

式中：Wf、Wi、Wa、Wo和Uf、Ui、Ua、Uo为线性关系系数，即权重；bf、bi、ba、bo为计算偏倚；σ则是Sigmoid激活函数；⊙为Hadamard积.

细胞状态更新为

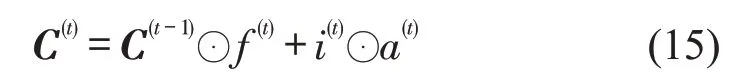
3.1 构建LSTM神经网络

本文构建了一个LSTM 循环神经网络如图8所示，该方法是在RNN 循环网络中嵌入LSTM 的神经单元.在t时刻下，网络的输入为观测的历史数据x(t)，输出为未来的预测数据，通过LSTM单元的输出h(t)得到

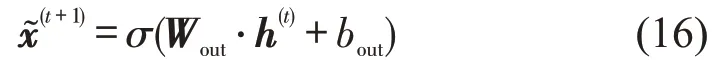
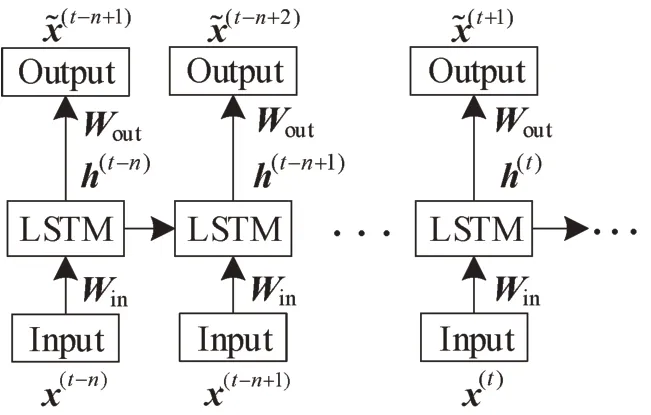
图8 LSTM 循环神经网络Fig.8 LSTM recurrent neural network

图8中，x(t)为历史观测数据，Win是输入层到隐藏层的权值矩阵，Wout则为隐藏层到输出层的权值矩阵，bout是输出偏倚.本文设置的输入为表1中连续的7条数据.

3.2 训练模型

降雨程度的不同，导致行程时间不确定.把降雨量分为0～6共计7个等级[7]其中0表示无降雨，降雨量和降雨等级关系如表2所示.在表1的基础上新增降雨等级特征，此时LSTM 的输入参数为：起始时刻、行程时间(s)、路段平均速度(km/h)和降雨等级4个特征量.

表2 降雨等级Table2 Precipitation level

基于时间序列预测的LSTM 模型中，主要的内部参数是隐藏层的维数和迭代次数，训练的同时也会生成参数之间的权重矩阵和参数偏倚.训练时将数据集分为3个部分：训练集(80%)，验证集(10%)，测试集(10%).网络依靠训练集对全局损失函数进行调整，通过验证集上的代价函数来选择模型中隐藏层的维数，最后通过测试集对预测性能进行评估.

最小损失函数Θ数学表达为

式中：Y表示实际观测的时间序列；是对应提前一步预测出行的时间序列.

损失函数为

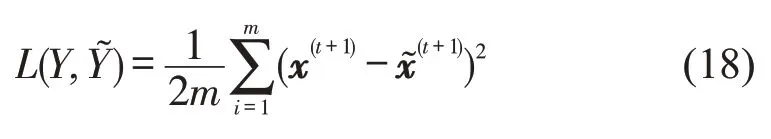
式中：m是预测旅行时间的个数.通过序列的反向传播计算损失函数对权值的梯度，公式为

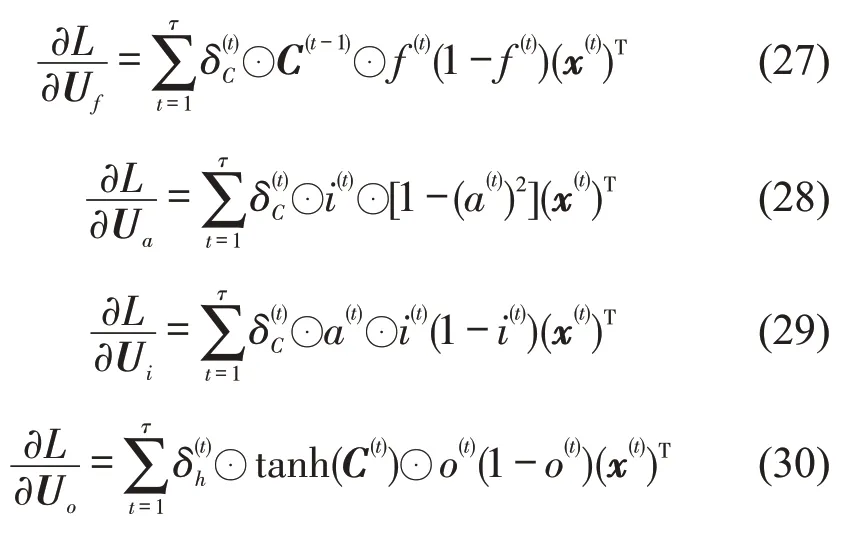
式中：表示t时刻下预测数据.

影响序列变化关系的重要计算步骤是损失函数L对隐藏状态h(t)和细胞状态C(t)的梯度求解，损失函数对状态偏倚的梯度求解与对权重求解类似.

3.3 结果分析

本文研究路段以苏州桥为起点，成府路与中关村东路交叉口为终点，途经苏州街路、北四环辅路和中关村东路.以出租车历史行驶GIS数据为研究对象，对将来某时刻为出发点途经该路程的行程时间进行预测分析.分别对2018年7月10日(晴天)的早高峰和7月17日(雨天)的早晚高峰和平峰时段的行程时间进行预测.预测数据如表3～表6所示.

表3 08：00-09：00 预测数据(2018-07-10)Table3 Prediction data at 08：00-09：00(2018-07-10)

表4 08：00-09：00 预测数据(2018-07-17)Table4 Prediction data at 08：00-09：00(2018-07-17)

表5 13：00-14：00 预测数据(2018-07-17)Table5 Prediction data at 13：00-14：00(2018-07-17)

表6 18：00-19：00 预测数据(2018-07-17)Table6 Prediction data at 18：00-19：00(2018-07-17)

与传统的BP、SVM 算法对比分析学习速度、预测误差和模型的可靠性[8]，同时选取均方根误差(ERMSE)监视计算过程中预测值与真实值之间的误差关系变化.

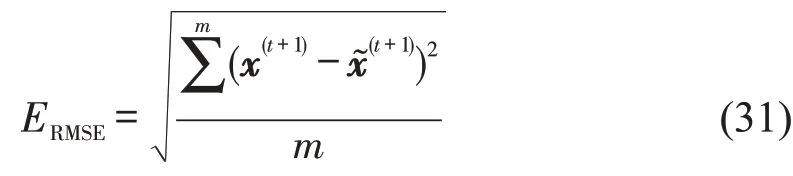
式中：ERMSE为均方根误差，m是预测旅行时间的个数.

使用偏差值95%置信水平下的置信区间来表示不同预测模型的可靠性.95%置信水平下的置信区间越小说明波动性越小，模型的可靠性越高；区间越靠近X轴误差越小.

(1)图9表明在预测结果上，此预测算法在保证预测精度为90%以上的准确率为0.75.加入降雨特征比未加入降雨特征预测的结果更准确，准确率由0.75上升至0.85.

(2)图10展示了在学习速度方面，BP、LSTM和SVM 存在较大的差异，分别是712，1 054，2 756 s.LSTM 神经网络的复杂程度比BP 神经网络大很多，但是在计算速率上并未相差太大.

(3)图11在可靠性上表明，LSTM 模型的置信区间比BP，SVM和Kalman都要小，说明该模型的偏差值波动较小，具有较高的可靠性.同时该模型的置信区间更接近X轴，说明预测值更接近于真实值.

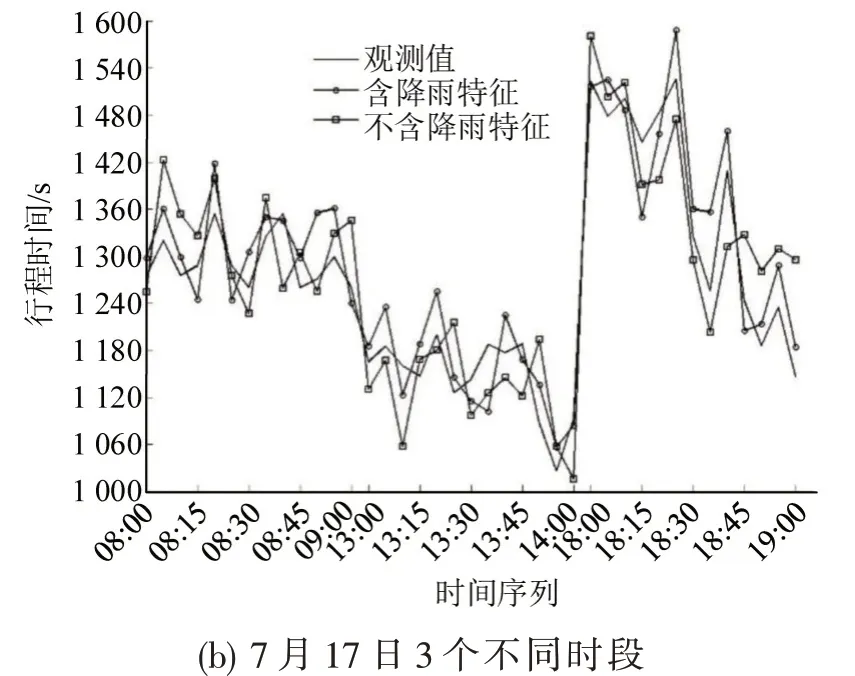
图9 不同时段的行程时间预测Fig.9 Prediction of travel time in different time

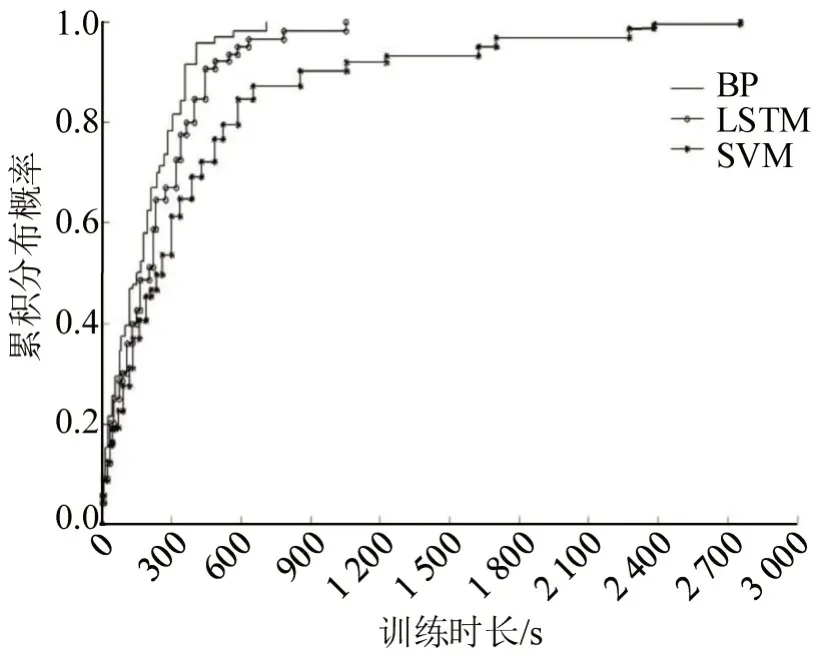
图10 链路的RMSE 累积分布Fig.10 Distribution of RMSE for each link

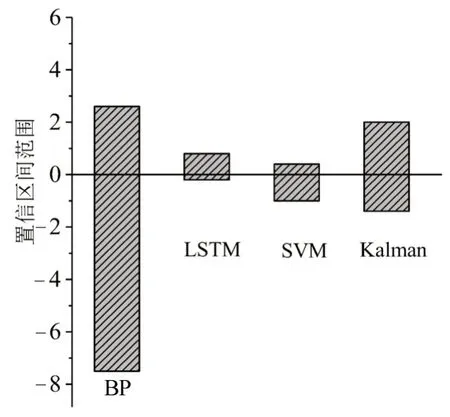
图11 可靠性分析Fig.11 Analysis of reliability

4 结 论

以北京市中关村西区出租车行驶的GIS 数据和北京市区域降水数据为研究对象，采用LSTM神经网络对行程时间进行预测分析.设计非最小路段的行程时间计算方法，结果表明，该方法具有更高的计算效率和更少的误差计算.对比分析BP、SVM 和Kalman 模型预测的结果.结果表明，在加入降雨特征的情况下，本文所用的LSTM 方法在满足精确度前提下拥有较快的训练速度和预测可靠性.本文的研究建立在良好的数据支撑上，对数据准确度要求较高.在后续的研究中应适当降低数据要求，提高该模型的可移植性.