考虑定制出行的儿童通学方式选择行为研究

郝京京，张 玲，吴小龙，杨晓泉，刘 澜

(1.西南交通大学交通运输与物流学院，成都610031；2.昆明理工大学a.云南省现代物流工程研究中心，b.综合交通发展与区域物流管理智库，昆明650500；3.昆明阡陌交通工程咨询有限公司，昆明650028；4.云南省交通运输厅路网监测与应急指挥中心，昆明650100)

0 引 言

儿童通学问题一直是困扰家庭的一大难题，引起政府决策者和学术研究者的广泛关注.儿童通学方式的决策主体往往是家长，家长普遍将儿童出行的安全性放在首位[1]，导致多数家长选择开车接送儿童上下学，引发了一系列社会问题.

基于此，国外学者对家长选择儿童通学方式的行为机理进行了研究，旨在揭示影响家长选择开车接送儿童上下学的主要原因.Stewart等[2]研究发现，影响家长选择开车接送模式的主要因素是通学的距离，家长更多关心儿童通学途中的安全性问题.Singh 等[3]基于多项Logit 框架构建了接送方式选择行为模型，并通过印度的实证研究发现，由于缺乏公共交通系统和高质量的校车服务，儿童通学出行决策过度依赖于其他机动化方式.近年来，越来越多的实证研究检验到家长开车接送儿童对家庭的消极影响，特别给双职工家庭带来了极大的负担；同时，对儿童身体健康和心理健康的消极影响也日益凸显.在这样的背景下，活跃出行方式(Active School Travel)逐渐成为关注的焦点.Smith[4]指出步行校车(Walking School Bus)是活跃通学出行的重要工具，既能缓解城市交通拥堵，又能促进孩子的身体健康、减少肥胖率.Pérezmartín[5]对步行校车在原有通学出行方式中的干预作用进行了研究，发现它对通学距离在1 500～2 000 m 范围内的家庭影响最大.国内学者则更多关注于儿童通学出行特征和家庭接送模式的研究.玛依拉·艾则孜等[6]基于多项Logit(MNL)模型建立考虑不同家庭结构的儿童通学方式选择模型，识别出了不同家庭结构类型下各类影响因素对儿童通学方式选择的具体影响.马书红等[7]将父母出行方式作为选择方程的自变量，儿童通学方式作为结果方程的因变量，运用Heckman Probit模型建立基于父母出行方式选择的儿童通学方式选择模型.景鹏[8]认为关注心理因素在通学出行方式选择中的影响非常重要，能够帮助更好地理解家庭在通学方式选择中的决策过程.

随着互联网技术的普及和推广，多数城市出现了一种定制出行方式——定制学生专线.定制学生专线是由专业的第三方公司介入，为儿童提供“一站式”“保姆式”的接送服务.然而，较少研究将定制出行方式纳入儿童通学方式选择范畴进行考虑.在研究方法选择上，以离散选择模型和结构方程模型为主，结合心理学和行为学去探讨通学行为的研究成果还相对较少.因此，本文将儿童通学方式分为小汽车出行方式、低碳出行方式、活跃出行方式和定制出行方式，构建家庭通学方式选择行为意向的结构方程模型，并进一步将行为意向作为通学方式选择效用函数的解释变量，最终形成儿童通学方式决策的HCM模型，用于探究定制出行方式介入后家庭对通学方式的决策行为.最后，选取云南省昭通市进行案例分析，旨在为定制学生专线等定制出行方式的开行和优化提供理论依据，进一步为有效缓解开车接送儿童上下学所带来的突出问题提供有效的解决模式.

1 变量选取

1.1 潜变量选取及测量

结合通学行为决策过程，影响出行方式选择的因素包含行为意向、出行限制、满意度和服务质量[9-10]，本文潜变量选取结果如表1所示.为保证潜变量量表的有效性，于2017年7月底在云南省昭通市进行了预调研.本次预调研共发放问卷69份，其中有效问卷52份.利用SPSS对预调研数据进行可靠性分析，通过计算校正的项总计相关性和项已删除的Cronbachα系数对初始量表的测量题项进一步提纯和净化，通过删除CITC小于0.3或删除后量表的Cronbachα系数值提升最高的题项，最终形成了包含31个题项的正式量表，如表1所示.

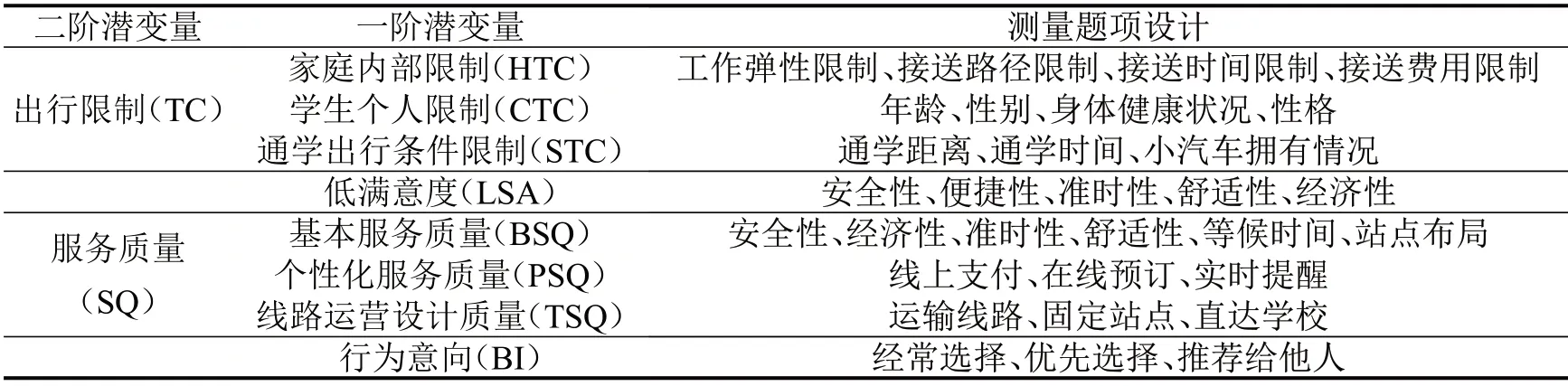
表1 潜变量选取结果及对应测量题项Table1 Selection results of latent variables

1.2 显变量选取

在显变量的选择中，主要考虑家庭特征、属性特征和接送方式属性.关于影响儿童通学方式决策的家庭特征属性，通常包括收入、规模、家长工作状态、小汽车拥有情况等因素[11].在接送方式属性变量选择上，时间和费用是两个重要的影响因素，通常被用来作为划分方式特性的关键变量[8].因此，本文显变量主要选取家庭收入，家庭人口规模，家庭非工作者比例，家庭老人比例，时间和费用6个变量.

2 模型构建

目前，用于研究儿童通学方式选择行为的模型主要有离散选择模型和结构方程模型.传统的离散选择模型在解释行为选择上具有一定的局限性，而结构方程模型却在揭示不可观测的潜变量对选择行为意向或结果的影响上具有明显的优势.在此背景下，将结构方程模型和离散选择模型结合起来的HCM 模型逐渐成为出行方式选择行为研究的热点.本文依据Ben-Akiva 等[12]提出的理论框架，构建了儿童通学方式的HCM模型，如图1所示，图中，ηBI表示行为意向，ηTC表示出行限制，ηLSA表示低满意度，ηSQ表示服务质量，ηHTC表示家庭内部限制，ηCTC表示学生个人限制，ηSTC表示通学出行条件限制，ηBSQ表示基本服务质量，ηPSQ表示个性化服务质量，ηTSQ表示线路运营设计质量.

2.1 模型定义

结构方程模型一般由测量模型和结构模型两部分组成.测量模型用来描述测量变量和对应潜变量之间的因果关系，可以表示为

式中：Cqp为测量变量，p为测量变量个数，q为家庭样本个数；ηFlq为一阶潜变量，l为一阶潜变量个数；ηSmq为二阶潜变量，m为二阶潜变量个数；γpl和hlm为待估系数；ζpq和τlq为误差变量，服从均值为0的正态分布.

结构模型则用来描述潜变量之间、潜变量与显变量之间的因果关系，可以表示为

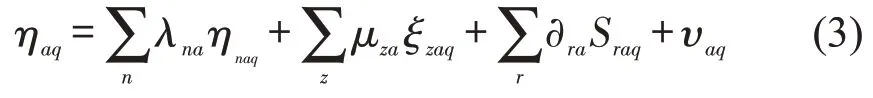
式中：ηaq为内生潜变量，a为内生潜变量个数，q为家庭样本个数；ηnaq为与ηaq相关的内生潜变量，n为与ηaq相关的内生潜变量个数；ξzaq为外生潜变量，z为外生潜变量个数；Sraq为显变量，r为显变量个数；λna、μza和∂ra为待估参数；υaq为误差变量，服从均值为0的正态分布.

在获取变量间因果关系的基础上，根据效用最大化原则，进一步获取出行者的选择结果，可以表示为

式中：yiq表示家庭q是否选择方案i的结果；Uiq表示家庭q采用第i种出行方式的效用，该函数包含潜变量和方式属性特性显变量，可表示为

式中：Xkiq表示出行方式属性；k为出行方式属性变量个数；ηgiq表示与效用函数有直接影响关系的潜变量，g表示与效用函数有直接影响关系的(内生和外生)潜变量个数；θki和βgi为待估参数；εiq为误差变量，服从均值为0 且独立同分布的Gumbel分布.

其中，出行方式i的选择概率可定义为

式中：Xiq表示家庭q选择出行方式i的属性变量；ηiq表示家庭q选择出行方式i的潜变量；θ和β为待估参数.

2.2 模型估计

首先，由于潜变量个数的增加会提高HCM模型参数估计的难度，因此采用三步法则对所构建的理论模型进行识别.具体步骤为：

Step 1利用验证性因子分析方法检验结构方程模型中测量模型的可识别性.

Step 2检验结构方程模型中结构模型的可识别性.

Step 3将结构方程模型中的潜变量和显变量作为离散选择模型中的解释变量，进一步检验离散选择模式的可识别性.

其次，考虑到样本数据的峰度和偏度值均在大于2和小于7的范围内，满足使用最大似然估计法(Maximum Likehood,ML)的准则，因此估计方法采用ML法，似然函数表示为

式中：Py(⋅)表示选择模型的概率函数；f(⋅)表示测量模型的密度函数；g(⋅)表示结构模型的密度函数；Ciq表示家庭q出行方式i对应的测量变量值；Sq表示家庭q对应的家庭属性变量；η表示潜变量；ηq为家庭q对应的潜变量；γ，h，λ，μ，α为待估参数；ε，ζ，τ，υ为误差变量.在参数估计和检验的过程中，采用Z检验法进行显著性检验，去掉Z检验达不到显著性水平( ||z≤1.96)的变量，并经多次试验，得到HCM模型的参数估计和检验结果.

3 数据收集

数据收集工作于2017年8月2～8日在云南省昭通市昭阳区进行，采用分层随机抽样方法(按照居民住宅区的房价水平进行分层)，随机选取3 个居民住宅区，根据各居民住宅区的住户数按比例分配抽样.样本含量的估计是根据分层随机抽样的样本量估计公式，计算出最小样本量为516户家庭.调查方式为在居民小区内部休闲娱乐场地、小区进出入口等地，通过主动询问的方式开展调查.综合考虑有效问卷率及调查费用的实际情况，共发放问卷600 份，回收问卷558 份，回收率为93.0%.通过对问卷的筛选，剔除了有缺失数据的问卷，最终获取545 份有效问卷.样本的特征统计如表2所示.

4 结果分析

在对模型进行求解时，要进行信度和效度的检验.结果显示，各潜变量的Cronbach'sα值均超出临界值0.70，CR 值在0.79～0.89 范围内，也超出了临界值0.70，表明测量指标具有良好的内部一致性信度.因此，量表通过信度检验.测量变量与所属一阶潜变量间的标准化载荷系数超出了标准值0.40，8 个潜变量的AVE 值均大于临界值0.50，潜变量间的相关系数的绝对值也小于AVE 的平方根，表明潜变量之间具有较强的聚合效度和区分效度.因此，量表通过效度检验.

以小汽车方式作为效用基础项进行回归分析，模型估计结果如表3所示.

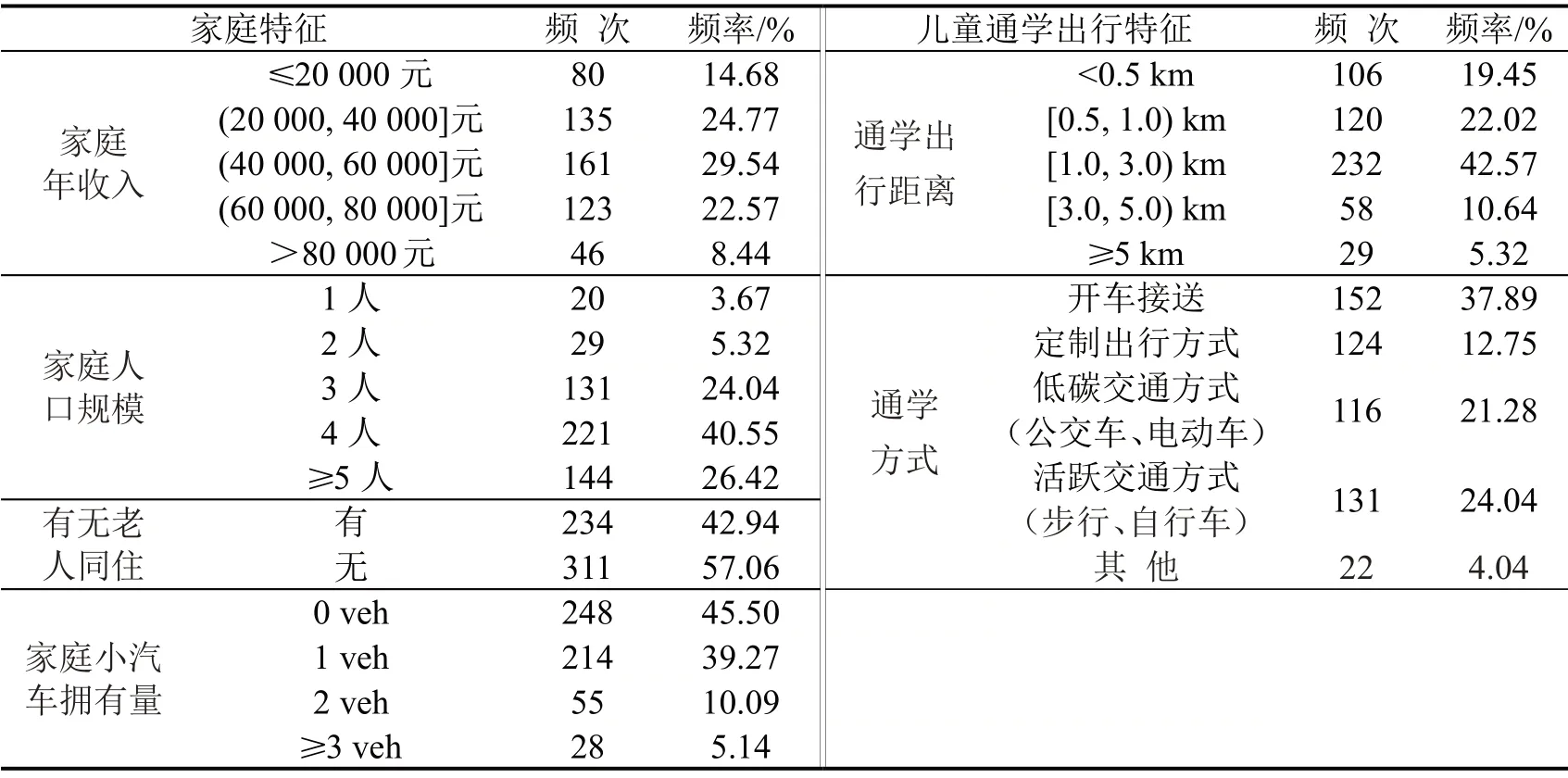
表2 研究样本特征(N=545)Table2 Study sample characteristics(N=545)

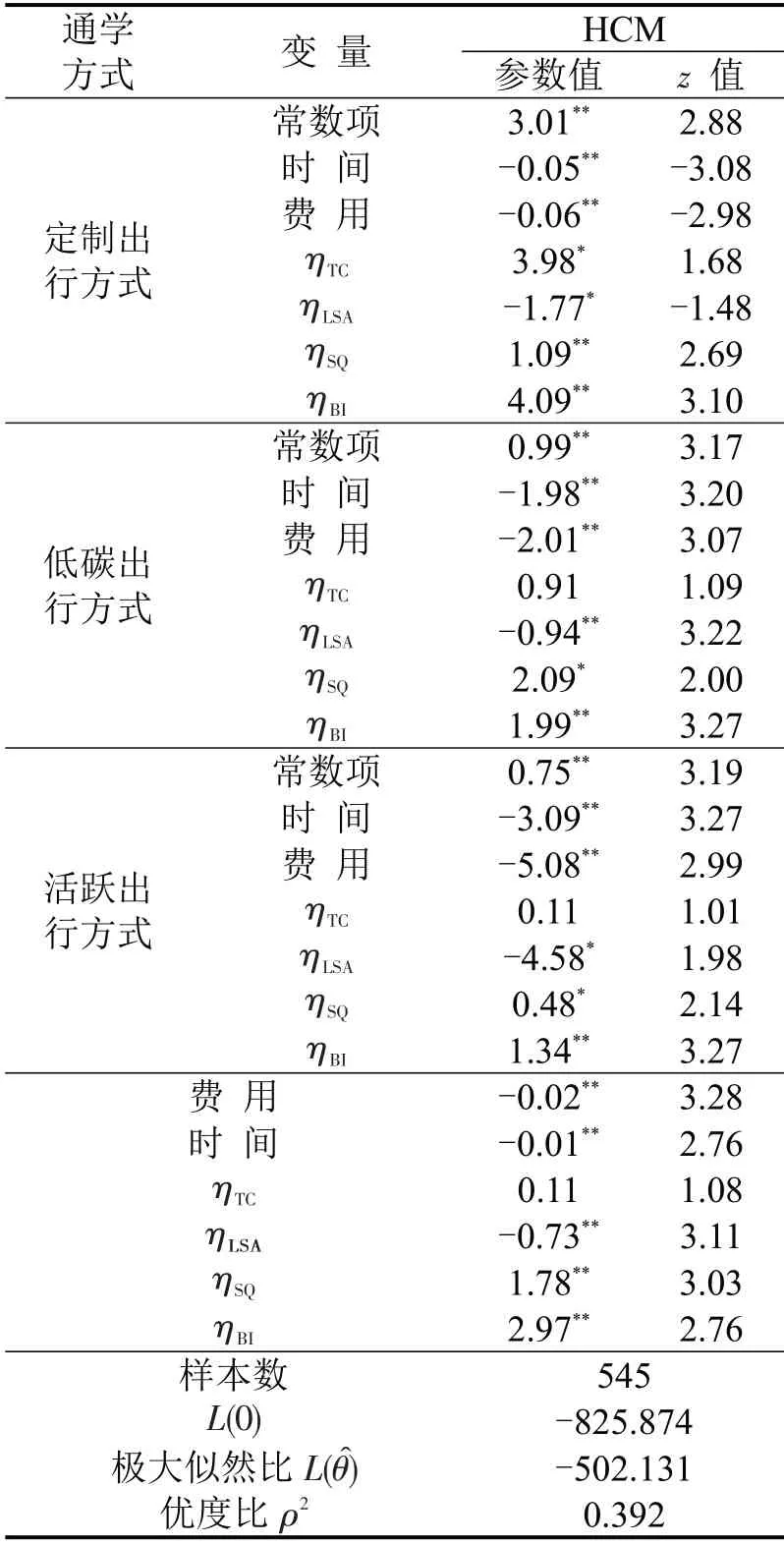
表3 HCM 模型参数计算结果Table3 Result of parameter estimation of HCM model

可以看出：

(1)将不带潜变量的MNL 模型结果与所构建的HCM模型结果进行比较分析，模型的参数估计和检验结果显示，增加了潜变量的HCM模型的各项检验指标均比未考虑潜变量的MNL模型更优，其中优度比ρ2由0.215上升到了0.392，说明HCM模型的解释能力明显提升，各潜变量在儿童通学方式选择行为中起着重要的作用.

(2)在定制出行方式初步发展阶段，小汽车出行仍然是家长的主要选择.从表3可以看出，行为意向(ηBI)对定制出行方式选择行为的影响作用最大，说明定制学生专线等定制出行方式的普及和推广取决于家庭的接受和依赖程度.同时，出行限制(ηTC)仅对定制出行方式选择行为存在正向影响作用，说明定制学生专线等定制出行方式作为一种“门到门”的一站式服务模式，随着家庭出行限制的增加，多数家庭更加倾向于选择定制出行方式，从而减少家长接送负担，缓解家庭出行限制.

(3)相比低碳出行方式和活跃出行方式，家长对于定制出行方式的时间和费用敏感性较低.从表3可以看出，家长更为关心低碳出行方式和活跃出行方式的时间和费用，影响系数均大于1，说明时间和成本并非家长选择定制出行方式的首要考虑因素.

5 结 论

儿童通学问题一直是热点问题，本文将定制出行方式纳入通学方式选择行为的研究范畴，通过构建儿童通学方式的HCM模型，对儿童通学方式的选择行为进行定量刻画和深度解析，旨在为定制学生专线等定制出行方式的开行和优化提供理论依据，也为当前儿童通学问题提供一种有效的解决模式.

研究发现：所构建的HCM模型相比传统不带潜变量的MNL模型具有更高的拟合度，说明HCM模型的解释能力明显提升，各潜变量在儿童通学方式选择行为中起着重要的作用；相比小汽车出行方式，行为意向对家长选择定制出行方式的影响更大，定制出行方式的普及更多取决于家庭的接受和依赖程度，出行限制也是影响定制出行方式选择的因素，随着家庭出行限制的增加，多数家庭更加倾向于选择定制出行方式，从而减少家长接送负担，缓解家庭出行限制；相比低碳出行方式和活跃出行方式，家长对定制出行方式的时间和费用不敏感，时间和成本并非家长选择定制出行方式的首要考虑因素.