基于贝叶斯建模的轨道占用识别方法

郭子明，蔡伯根,b,c，姜 维*,b,c，王 剑,b,c，上官伟,b,c

(北京交通大学a.电子信息工程学院；b.轨道交通控制与安全国家重点实验室；c.北京市轨道交通电磁兼容与卫星导航工程技术研究中心，北京100044)

0 引 言

为保证列车运行安全，列车控制系统不仅需要具备在铁路线路上的连续定位能力，还须识别当前列车所在轨道，即轨道占用识别，为列车自动运行、避撞等相关安全应用提供必要的信息支撑.相对于依赖地面设备(应答器、计轴器等)的传统列车定位技术，基于车载传感器的列车自主定位技术在保证提供列车位置服务的前提下，能够大大降低地面基础设施的建设与维护成本.随着全球导航卫星系统(Global Navigation Satellite System,GNSS)的不断发展与完善，对以其为基础的列车车载定位技术的研究成为了下一代列车控制系统的研究内容之一[1-2].GNSS 在某些特定铁路运行环境下不能满足精度与可用性上的要求，所以GNSS通常与其他传感器组合，比如车轮传感器[3-4]、惯性传感器(Inertial Measurement Unit,IMU)[5]等，共同实现列车定位功能.此外，由于铁路线路对列车位置的一维限制，为提高定位精度，数字轨道地图也成为列车车载定位技术中不可或缺的组成部分.

王剑等[6]采用GNSS 测量数据，提出一种基于隐马尔科夫模型的轨道占用识别方法.Katrin Gerlach 等[7]提出一种基于多假设的垂直投影地图匹配方法，对GPS、IMU和雷达传感器数据进行融合，在贝叶斯估计的基础上对各假设进行剔除和选择，实现轨道占用识别.吴波前等[8]在非确定性地图匹配算法的基础上，综合分析GNSS数据包含的距离与方向信息，建立多条轨道线路的权重函数，从而完成列车所在轨道的识别.上述研究只聚焦于轨道占用识别，忽略了其与列车位置决策的关联.此外，研究者们没有从轨道占用识别的距离延迟方面进行分析.

为了解决上述问题，本文以贝叶斯建模的方式对列车位置假设进行描述，计算给定测量条件下不同假设的概率；通过地图匹配将GNSS和速度传感器信息进行融合，同时完成对列车在轨道地图中一维位置的确认及所在轨道的识别.该方法利用卡尔曼滤波算法对速度传感器的测量数据进行误差分析，将GNSS测量的误差曲线引入各假设的概率计算过程中，对不同的轨道占用识别结果进行分类.

1 定位传感器与数字轨道地图

定位传感器包括1套GNSS接收机和1个速度传感器.GNSS接收机作为列车车载定位系统的基础，提供WGS84 坐标系下的列车绝对位置测量.一帧GNSS 测量数据包括纬度值、经度值及表示纬度与经度方向测量不确定度的协方差矩阵

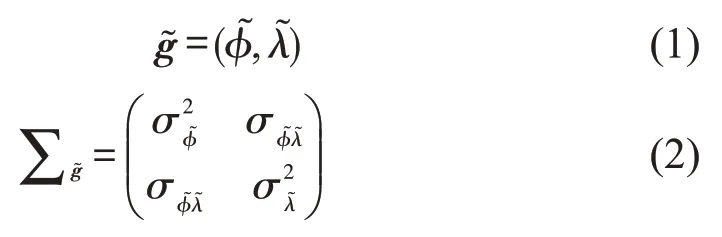
式中：为纬度方向上的测量标准差；为纬度与经度的测量协方差；为经度方向上的测量标准差.

速度传感器用来测量列车运行速度，并判断列车运行方向，即给出带符号的速度测量值v.本文方法不依赖于特定的传感器，可采用支持不同星座的GNSS 接收机(GPS、北斗等)和不同测速原理的速度传感器(车轮传感器、多普勒雷达、涡流传感器等).

数字轨道地图基于railML格式[9]生成，由连接节点(nodes)和轨道区段(tracks)构成，如图1所示.用于表示连接节点位置的地理信息(coordinates)包括纬度，经度，在铁路网中的沿轨道方向的一维位置及其编号.轨道区段通过连接节点相连，且不同轨道区段具有唯一的轨道标识符(ID).轨道区段的曲线段近似由一组相连的直线段表示.

图1 数字轨道地图内容Fig.1 Contents of digital track map

2 轨道占用识别

图2对轨道占用识别问题进行了描述.当列车行驶经过道岔后，列车真实位置可能位于GNSS测量点附近的多条轨道上(列车位置1或列车位置2).一方面需要根据车载传感器获取的列车位置信息判断列车当前所在轨道，另一方面需要确定列车在该轨道上的相对位置.

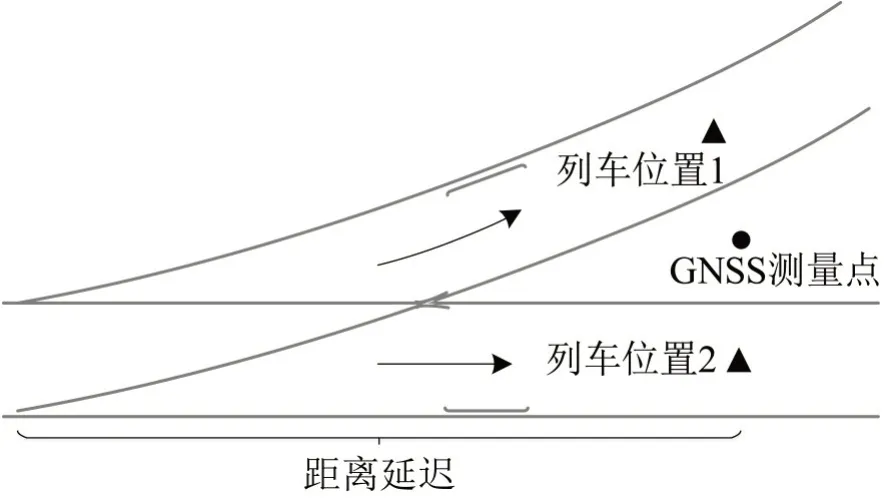
图2 轨道占用识别描述Fig.2 Description of track occupancy identification

2.1 列车位置描述

列车位置状态包括列车当前所在轨道t、列车运行方向o及列车沿轨道方向一维位置l.列车运行方向o表示列车正在向前行驶(o=+1)或向后行驶(o=-1).虽然列车运行速度也是描述列车位置状态的因素，但本文只将其运用于一维位置的决策中，不作为独立的状态变量考虑.

为处理传感器的测量误差，采用基于贝叶斯建模的假设检验方法，生成多个位置假设来描述不同列车位置的可能性.考虑轨道占用识别的需求，每个假设都应包含路线信息，即每个假设包含多条轨道区段，且具有明确的运行方向信息.图3给出2 个位置假设的示例，即假设h1从T1延伸至T2，假设h2从T1延伸至T3，两假设具有相同的运行方向，S1表示1个道岔连接节点.

图3 包含路线信息的位置假设示例Fig.3 Example for two hypotheses with route information

每个假设中，列车沿轨道方向的一维位置由一个高斯分布表示.在同一个轨道区段上可能存在多个假设，因此关于列车位置的总体分布可以看作是高斯混合模型[10]，表示为

式中：f(t,o,l|h)描述在给定假设的条件下沿轨道方向位置l的分布；P(h)为该假设正确的概率.

2.2 考虑GNSS定位误差的地图匹配

在列车的相对定位中，通常采用地图匹配的方法将GNSS 的二维位置坐标转化为轨道地图中的一维位置表示.最常见的地图匹配通过垂直投影的方式来实现.虽然垂直投影法可以简单快速找到地图关联点，但没有考虑当前GNSS测量点的不确定度.故提出一种基于方向相关的GNSS标准差的地图匹配方法.

GNSS 测量点的二维误差分布可以用误差椭圆表示.然而，误差椭圆只能提供椭圆长轴方向和短轴方向的测量误差，不能描述其他位置的误差信息.故采用误差椭圆对应的垂足曲线来确定任意方向的测量标准差σpos.

图4给出了GNSS 测量点的误差椭圆及对应的垂足曲线，椭圆长半轴长，短半轴长.在椭圆上任一点Q作椭圆的切线，从坐标原点向该切线引垂线，垂足为P，则垂足P的轨迹构成了误差椭圆的垂足曲线.GNSS测量点与垂足P之间的距离，即该方向上的测量标准差.垂足曲线在极坐标系下的表达式为

式中：α为GNSS 测量点与垂足P的连线与椭圆短半轴的夹角.

图4 GNSS 测量点的误差椭圆和垂足曲线Fig.4 Error ellipse and pedal curve of GNSS measurement

为了将与方向相关的GNSS 标准差应用于后续假设概率计算中，将垂足曲线进行放大或缩小，使其与当前测量点邻域内的轨道区段相切，如图5所示.垂足曲线经过放大后与轨道区段T2相切，相切点PM被认为是GNSS 测量点在T2上的地图匹配点.地图匹配点PM的坐标及该方向的测量标准差σpos都可根据式(4)计算得到，在已知轨道区段T2端点的坐标及沿轨道方向位置的前提下，点PM的一维位置lGNSS也可推导得出.lGNSS和σpos将应用于2.3节中.

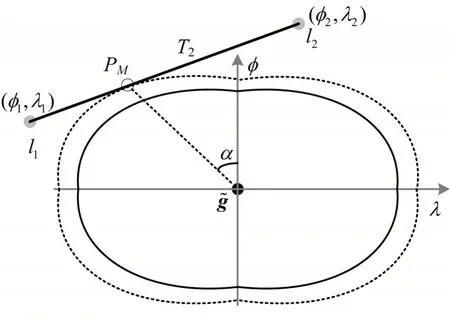
图5 基于方向相关GNSS 标准差的地图匹配Fig.5 Map matching based on direction-dependent GNSS standard deviation

2.3 列车位置决策

列车沿轨道方向的位置l通过GNSS 与速度测量的融合获得.假设GNSS 与速度测量相互独立，并利用单独的传感器信息计算得到两个列车沿轨道方向位置lGNSS和lv，其中lGNSS已在2.2 节中得出.

认为列车在短时间内保持匀速运动，列车位置lv表示为

式中：l为算法上一周期内计算得到的列车位置；为当前速度测量值；T为速度测量的更新周期.

独立计算得到的列车位置lGNSS和lv通过加权求和的方式进行融合.权重因子由列车位置的不确定度决定，即对应的方差.lGNSS的方差σ2GNSS定义为GNSS 测量点与其对应地图匹配点之间距离平方的期望，可根据式(4)迭代计算得到，lv的方差σ2v则利用卡尔曼滤波算法进行估计.

在卡尔曼滤波的时间更新过程中，对先验状态变量v进行预测.之后在量测更新过程中引入速度测量从而获得其后验估计.与σ2GNSS相似，把速度预测与后验估计差值平方的期望当作lv的方差σ2v.

最终的列车位置l为

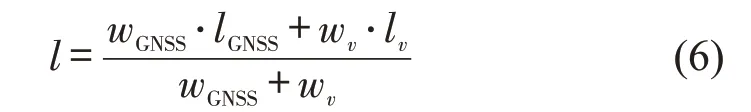
在给定GNSS测量与速度测量的条件下，列车当前所在轨道t、运行方向o及列车位置l的概率表示为

根据假设h与列车位置l可直接判断其是否位于轨道区段t上，故式(7)等号右侧第1项的取值是确定的(1或0).

如果列车位于轨道区段t上，假设轨道区段t的端点坐标分别为(ϕ1,λ1)和(ϕ2,λ2)，沿轨道方向一维位置分别为l1和l2.式(7)等号右侧第2项作为高斯分布，可表示为

式(7)等号右侧第3个条件概率可以转换为

假设在给定轨道区段t的条件下，GNSS 测量点到该轨道区段的距离符合高斯分布.因此，式(9)右侧第1项可表示为

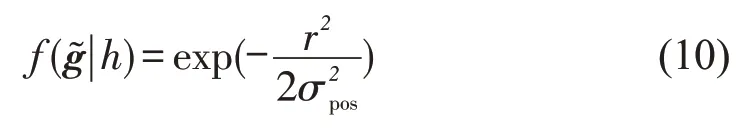
式中：r为GNSS测量点与其地图匹配点之间的距离；σpos为对应方向上的测量标准差，两者的推导过程见2.2节.

式(9)右侧第2 项假设h的先验概率P(h)，可以由算法上一周期中的后验概率代替.然后，对所有假设的条件概率进行归一化处理.

2.4 假设剔除

在算法的每一个循环内，通过比较所有假设的概率确定当前的列车位置.在一个复杂的铁路网中，可能产生大量的假设，对可能的列车位置进行建模.然而，当GNSS 测量点逐渐远离这些假设的时候，对应的概率会迅速减小.为保证算法的效率，须及时剔除那些不可能的假设.由于位置假设符合高斯分布，其概率不会减小至0.将剔除假设的概率阈值设置为10-10，该值低于列车应用可接受的失效率，从而保证系统安全.只要某假设的概率小于该阈值，则将其从假设集中剔除.

3 实验结果与分析

3.1 实验描述

采用一辆安装有一套GNSS 接收机和车轮传感器的铁路实验车，在铁路实验场采集数据.该实验场地铁路线路长度共约30 km，具备多种道岔及平行股道场景，如图6中A点到B、C点到D点.采用的数字轨道地图通过Open Street Map[11]生成.

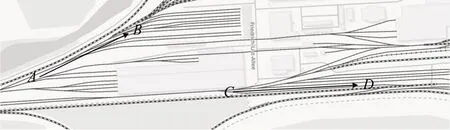
图6 实验场地Fig.6 Test ground

实验共采集8组数据(D1,D2,…,D8)，经过48个单开道岔，其中对向通过40 个，背向通过8 个.只有当列车对向经过道岔时才会出现轨道占用识别场景，对所有8组实验数据的GNSS与速度数据的时序进行反转，从而获得48 个对向道岔(其中8 个经过反转产生).

3.2 结果分析

本文假设，在列车对向经过道岔处于轨道占用识别场景时，只有所有小概率假设全部被剔除，即只存在一个列车位置假设，轨道占用识别才被最终确认.

在列车经过少数道岔后，由于道岔间距离较小，在到达下一道岔前不足以剔除所有小概率假设，轨道占用识别无法完成，因此这部分特例不会在后续实验结果中出现.图7给出对8组实验数据分别采用垂直投影法[7]和本文提出的基于贝叶斯建模的定位方法完成轨道占用识别所需距离(经过岔尖后)的统计结果.对所有8组数据而言，基于贝叶斯建模的定位方法的轨道占用识别效果均优于垂直投影法.其中，对第6 组数据采用垂直投影法实现轨道占用识别需要的平均距离为39.6 m，而采用基于贝叶斯建模的定位方法需要37.6 m，两者相差2 m，为8组数据中最小.对第8组数据采用本文方法后轨道占用识别性能提升最显著，比垂直投影法的平均距离减少9.9 m.总体而言，对列车所在轨道的识别能力依赖于不同的道岔场景.

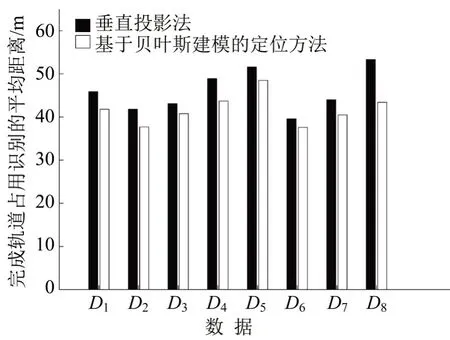
图7 完成轨道占用识别的平均距离Fig.7 Mean distances that track occupancy identification requires

图8给出两种方法完成轨道占用识别所需的距离分布情况.垂直投影法在经过道岔后至多55 m可以判定列车所在轨道，基于贝叶斯建模的定位方法则在53 m内完成轨道占用识别.

由GNSS 与速度测量融合得到的沿轨道方向的位置误差如图9所示.40%的定位结果对应的标准差小于1 m，87%的定位结果小于2 m，而所有定位结果的标准差均小于3 m.

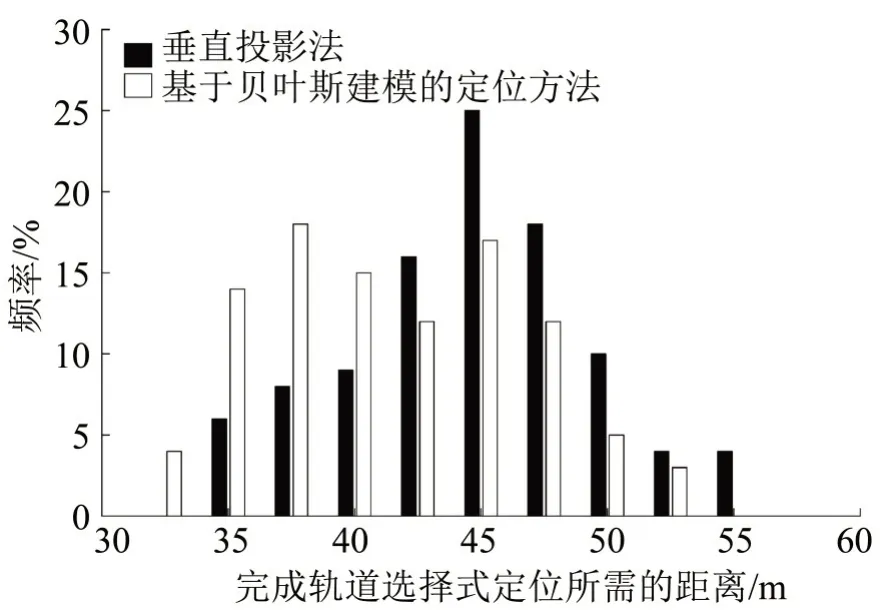
图8 轨道占用识别所需距离的频率分布Fig.8 Frequency histogram of distance to track occupancy identification

图9 沿轨道方向位置标准差的频率分布Fig.9 Frequency histogram of standard deviation of longitudinal train position

根据通过道岔的最大速度，可将所有道岔场景分为3组，表1给出在不同速度条件下采用不同方法完成轨道占用识别的平均距离.方法I表示垂直投影法，方法II 表示本文提出的基于贝叶斯建模的定位方法.

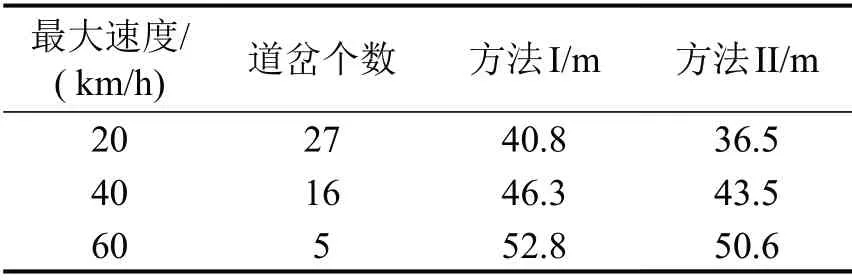
表1 不同速度下轨道占用识别所需平均距离Table1 Mean distances for track occupancy identification at different velocities

将所有定位结果分为6个类别，进行进一步对比分析：

(1)非常确定的错误轨道(wrong track,confident，WC).算法将一条错误轨道作为轨道占用识别结果.该类别的定位结果会对列车安全相关应用造成严重后果.

(2)相当确定的错误轨道(wrong track,fairly confident，WF).算法选择一条错误轨道作为列车当前所在轨道，并认为该判断的正确概率大于0.9.

(3)不确定的错误轨道(wrong track,undecided，WU).算法选择一个错误的位置假设，其概率小于0.9.

(4)不确定的正确轨道(correct track,undecided，CU).算法选择正确的列车位置假设，但其概率小于0.9.

(5)相当确定的正确轨道(correct track,fairly confident，CF).算法正确识别列车当前所在轨道，并认为该判断的正确概率大于0.9.

(6)非常确定的正确轨道(correct track,confident，CC).算法正确识别列车当前所在轨道，且无其他位置假设存在.

图10给出了定位结果在不同类别上的分布.两种方法都没有将错误轨道作为轨道占用识别结果，但显然基于贝叶斯建模的定位方法更加确定对正确轨道的识别，而垂直投影法大多数时间并不保证其轨道识别的正确性.

图10 不同定位结果类别的频率分布Fig.10 Frequency histogram of different categories of localization results

4 结 论

本文研究了基于贝叶斯建模的列车轨道占用识别方法，根据列车在道岔处可选择的不同路线信息，生成列车位置假设，在利用GNSS 与速度信息融合获得列车沿轨道方向位置的前提下，采用高斯混合模型描述列车位置，将列车位置决策与所在轨道识别关联起来.通过对实验结果的分析，本文方法有效减少了剔除假设所需的距离延迟，并从安全层面验证了其优点.基于GNSS接收机和速度传感器的结合，本文为轨道占用识别提供了基本的贝叶斯模型框架，下一步工作将引入其他道岔检测传感器，对道岔进行建模识别，提高算法鲁棒性.