基于半监督哈希算法的交叉口交通状态识别

张立立，王 力，赵 琦，张玲玉

(北方工业大学城市道路交通智能控制技术北京重点实验室，北京100144)

0 引 言

交叉口的交通状态具有多维度、复杂性和时变性等特点，准确辨识交通状态是实施有效交通控制策略的前提.国内外学者针对交叉口交通状态识别的研究主要面向过饱和状态识别，并集中在以下两类.

一类是不考虑检测方式，利用基本交通统计数据，通过设计参数指标进行的交通状态判别研究.Gazis[1]最早给出交叉口过饱和定义，提出基于饱和度识别的方法；Dion等[2]提出基于延误时间比较的交叉口交通状态识别方法；陈兆盟等[2]将车头时距的方差与时间占有率作为参数，结合周期排队车辆的消散，提出一种结合信号优化的交通状态识别方法；吴志勇等[4]从深度学习角度出发，提出一种离散化交通状态识别方法；张立立提出以饱和度为基础的交叉口交通状态精细化识别方法[5]和基于综合投影的交叉口交通状态识别方法[5].

另一类是考虑检测方式，利用检测器特性，通过检测得到的统计数据估计排队长度进行的交通状态判别的研究.Liu 等[7]利用上下游部署线圈检测器，使用通过检测器的车辆数据估计排队长度，进而识别交叉口的过饱和状态；钱喆等[8]在文献[7]的基础上完善了识别方法；Ban 等[9]通过移动检测数据测量车辆的旅行时间，进而估计出排队长度以识别交叉口过饱和状态，而Li 等[10]则是从移动检测的轨迹数据设计辨识方法；Antoniou 等[11]和Wang 等[12]分别从多源动态数据入手，分析交叉口过饱和状态；Wu等[13]和刘云翔等[14]利用RFID数据估计排队长度，得到过饱和状态；唐少虎等[15]以上下游视频检测的车牌数据为基础，通过计算车辆通行的延误时间来估计最大排队长度以实现交叉口状态判别.

以上两类研究，都是利用统计数据，如流量、车辆数、密度等进行包括排队长度的估计或饱和度等参数的计算，以实现交叉口交通状态的判别.但由于统计数据的粒度粗、周期特性强，本质上忽略了原始数据的丰富性，无法精细识别交叉口时间序列上的全部交通状态.基于此，从先进检测手段的原始数据丰富特征入手，构建交叉口有效检测区域的图像化模型，利用半监督哈希算法实现图像搜索，进而得到交叉口的精细化交通状态.

1 交叉口图像化模型构建

1.1 原始检测数据与扩展离散编码

(1)检测器的原始数据.

传统用于交通控制的数据类型包括流量、占有率、密度、排队长度等，这些类型的检测数据具有检测粒度粗、统计特性强的特征，难以有效描述实时动态交通变化的细节.随着雷达检测技术和车路协同技术的发展，实时的高精度轨迹跟踪式检测成为可能，正逐渐应用到城市道路交通控制中，如图1所示.该类检测手段可提供的实时数据(毫秒量级)包括瞬时车速(Xspeed,Yspeed)、车辆位置(xpos,ypos)、车辆身份、车辆长度和时间戳5 类数据.基于这些类型数据的全样本实时高精度轨迹跟踪式检测数据，能够充分反映检测区域内真实的交通变化.

图1 实时高精度轨迹跟踪式检测Fig.1 Real-time high-precision trajectory tracking detection

(2)交叉口有效检测区域描述.

虽然上述先进的检测手段能够获得实时高精度数据，但其依然受到检测范围和数据采集频度的约束，即检测精度在一定情况下受到检测范围影响，数据采集频度受到检测器计算能力和网络传输能力影响，为此需要给定有效检测区域和合理的数据采集频度.

为使检测数据尽可能完整地包含交通特性，在确定交叉口有效检测区域范围时，需要考虑路段当量排队长度约束和检测器最大检测范围约束.其中，路段当量排队长度约束可由二流理论得到，检测器的最大检测范围由实际检测方式决定.

式中：LD表示最小检测区域；LM表示最大检测区域；LP表示有效检测区域的东西距离(lp-length)和南北距离(lp-width)，LP=[lp-length,lp-width].

图2 交叉口的有效检测区域Fig.2 Effective detection area of intersection

(3)扩展离散状态编码.

通过合理表示车辆属性和运行状况，能够真实反映交叉口交通状态进而为实施有效的交通管控策略提供依据.传统检测数据的粗粒度和统计特性难以满足上述车辆属性和状况的描述，故采用一种扩展离散状态编码方法予以表示.

由式(1)可知，交叉口有效检测区域为LP=[lp-length,lp-width]，以当量小汽车长度l为标准，则可将车道划分为个单元.离散化后得到交叉口有效检测区域内的车辆属性和状况的向量Μ，表示为

式中：C向量表示存储车道单元是否有车辆存在的信息，其中C[i]=1 表示车辆存在；R向量表示存储车辆的速度信息；Z向量表示存储车辆的加速度信息；Q向量表示存储车辆的身份信息；N向量表示存储车辆的换道信息；l表示车辆占用道路的单位空间，由换算的标准小汽车长度()与平均车辆间距共同构成，

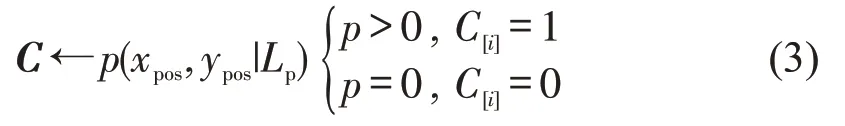
图3是t时刻某标准正交十字交叉口车辆属性和状况编码情况.

图3 扩展离散状态编码到图像化的映射Fig.3 Extend discrete state coding to graphical mapping

由式(2)和图3中表示以下数据形式.C向量表示存储车道单元是否有车辆存在的信息，如图4(a)所示，1 表示有车辆，0 表示没有车辆，这里描述的是真实的坐标数据映射至路段上的结果；R向量表示存储车辆的速度信息，如图4(b)所示，1 表示车速为自由流车速，0 表示没有车或车辆停止，其余取值由Sigmod 函数映射得到并且小数点后一位；Z向量表示存储车辆的加速度信息，如图4(c)所示，数值为负数表示车辆的减速运动，数值0 表示车辆的匀速运动，数值为正数表示车辆的加速运动；Q向量表示存储车辆的身份信息，如图4(d)所示，车辆的身份信息从最内侧车道开始计算依次编号，对于特殊车辆采用倒序编号，以最大数计；N向量表示存储车辆的换道信息，如图4(e)所示，0 表示车辆未换道，1 表示车辆换道后的位置，0.5表示车辆换道经过的位置.

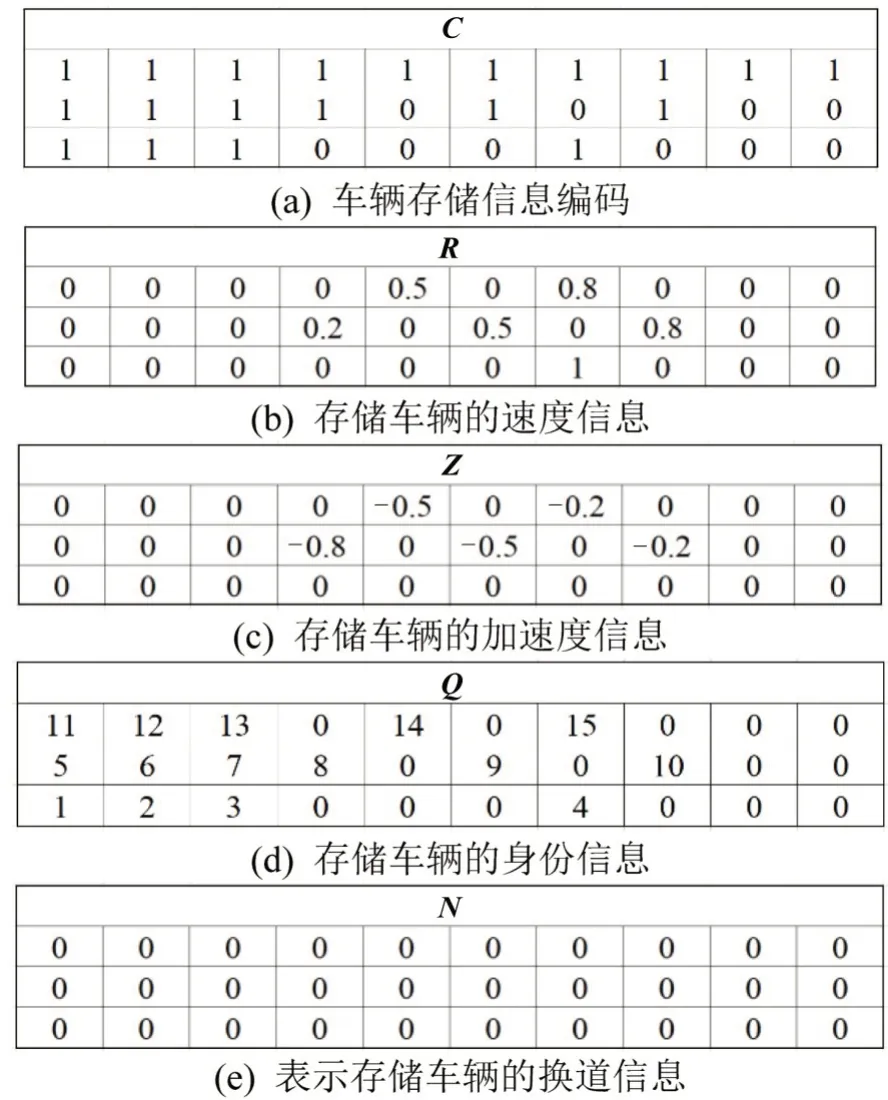
图4 扩展离散状态编码数据描述Fig.4 Data of extension discrete traffic state encoding

1.2 交叉口图像化建模

假设交叉口有效检测区域是由关键部分组成的集合Γ，表示为

式中：X是交叉口入口车道组成的集合，X={x1,x2,…,xm}，xi表示进口车道，m为进口车道数量；Y是交叉口出口车道组成的集合，Y={y1,y2,…,yn}，yi表示出口车道，n为出口车道数量；Z是交叉口冲突区域组成的集合，Z={z1,z2,…,zu}，zi表示冲突区域的分块，u是对冲突区域的分块数量，如图5所示.

集合Γ的状态值由五元组计算得到，即

式中：Μj表示离散化后得到交叉口有效检测区域内的车辆属性和状况的向量，η表示集合Γ中的一取值，wi为指标权重，

图5 交叉口关键部位组合Fig.5 Combination of key parts at intersections

eη∈Γ(t)采用平移修正处理的距离熵[16]确定：① 用距离熵计算指标的权重并计算最终的eη∈Γ(t)；②当分指标数值固定或变化幅度极小时，经归一化和标准化处理后距离熵的值为0.

采用数据平移修正的方法对这部分指标进行处理，保证所有分指标对eη∈Γ(t)起作用.设计分项指标矩阵

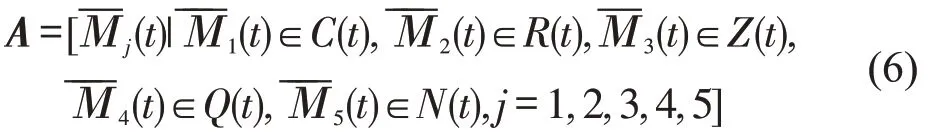
Step 1将A=[aj]5进行归一化处理，得到标准信息矩阵R=[rj]5.归一化的处理方法如下：对于越大越优型分指标

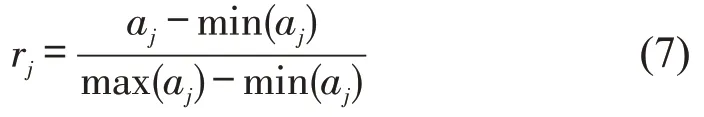
对于越小越优型分指标

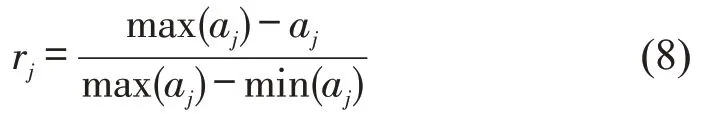
选择第j个指标所对应的最优单元值r*j，j=1,2,3,4,5，选取规则为

Step 2计算各指标rj对应的最优单元值的距离为

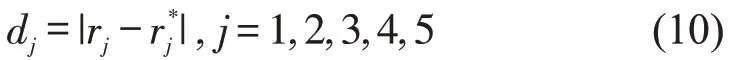
Step 3计算对应指标概率为

当dj ＞0 时，无需对βj进行修正，此时uj=0；当dj=0 时，该分指标对exi(t)不起作用，为保证所有指标数据的可用性，需人为的对βj进行平移修正，此时uj为常数，且uj ＞0.

Step 4计算指标的距离熵为

Step 5计算熵权为

Step 6综合指标eη∈Γ(t)为

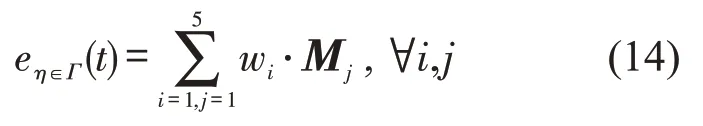
Step 7交叉口有效检测区域内的交通状态由关键部分的状态集合得到，即

交叉口入口、出口和冲突区域的状态值表示为

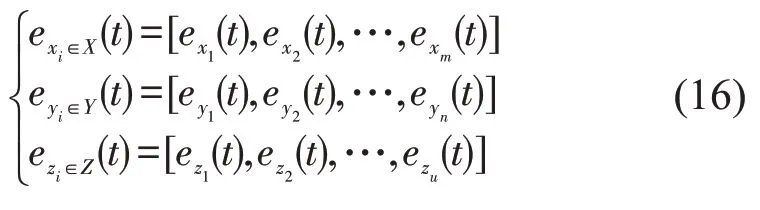
设计分段线性函数集合，以描述交叉口各关键部分交通状态与状态值之间的关系，即

将式(17)中分段线性函数进行向量转化，得到

由此可以得到交叉口的交通状态是由关键部分组成的集合Γ的状态值表示.交叉口交通状态集合为Ξ，即

式中：ξi如下所示，由于入口车道数m、出口车道数n和冲突区域分块数u并不能保证相同，因此为保证向量长度一致，对矩阵无向量位补0.

对式(20)进行如下变换，可以得到交叉口交通状态ξi的σ=m+n+u维的特征向量.

2 基于半监督哈希的交通状态识别

由1.2节内容，将交叉口的交通状态识别问题转化为对图像化搜索问题，本节采用基于半监督哈希算法实现图像搜索.基于半监督哈希算法[17-18]的交叉口的交通状态识别的核心思想是：通过扩展离散状态编码技术将交叉口有效检测区域内的交通变化转化成一种特殊形态的图片，利用半监督哈希算法实现以图搜图.

(1)构造目标函数.

定义目标函数为

(2)哈希函数学习.

对式(22)进行改造，将目标函数改写为

其中，式(23)中只有监督信息成分，加上非监督信息成分后，目标函数为

其中定义P为

最大化式(11)的解可以得到哈希矩阵W为

(3)哈希码生成.

由W矩阵中取出任意一个列向量，带入哈希函数中，可以为一个图像生成一位哈希码.至此，学习得到了对一个图像进行哈希编码的哈希函数族γ=[r1,r2,…,rK]，其中rK表示第K个哈希函数.

同时，考虑到交叉口的交通状态由交叉口的有效检测区域的关键部位的变量集合决定，因此令K=m得到哈希编码的比特数.

(4)相似性度量.

通过计算测试图像与训练库中图像的相似性度量函数可以实现图像搜索.

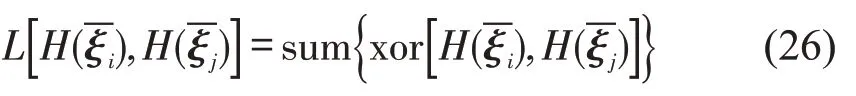
式中：xor(⋅)表示异或运算；sum(⋅)表示求和运算.

式(26)表示对于一个待查的图像，表示计算该图像的哈希码与训练库中图像的哈希码的汉明距离.汉明距离越小，表示该图像与查询图像越相似；反之，不相似.

3 实验与结果分析

3.1 实验参数设置

实验采用VISSIM仿真软件，通过其所提供给的COM和MATLAB搭建仿真环境.实验中定义具有上下游的正交十字交叉口，各方向均为双向两车道，上下游连接路段为500 m，交叉口的冲突区域为50 m×50 m；车辆构成为小型车95%，大型车5%；车速分布按照道路建设标准选取0～60 km/h；路段输入流量采用与实际道路相符合的变化趋势(包含平峰和高峰)；交叉口配时采用由Webster 计算的配时方案.给定的图像库的样本数为36 000(模拟检测器的采样频率为1 Hz/s)，其中，随机挑选样本数30 000作为训练数据集(具有标签的样本数为3 000)，剩余样本数6 000作为测试数据集，如表1所示.

表1 交叉口交通状态图像样本Table1 Image samples of traffic state at intersections

3.2 交通状态识别与分析

为验证所提方法，采用精细度EFI、准确率EAC和实效性ETM指标进行效果评价，公式定义为

式中：MTP表示被正确搜索到的样本数量；MFN表示被错误搜索到的样本数量；MTN表示非标签类型且未被搜索到的样本数量；MFP表示非标签类型且被搜索到的样本数量；MFE表示判别时间；MFT表示总搜索时间.

为使研究工作具有延续性，将本文与作者前期工作中的相关研究[5-6]进行比较，如表2所示.从结果分析比较来看，采用本文方法在交叉口的交通状态的精细度和实效性上均有较高提升.对于准确率来说，训练库中有标签样本的数量只占到总样本为10%，故提升的幅度不大，后续研究中将进一步提高有标签样本的占比，有望使得准确率继续提升.

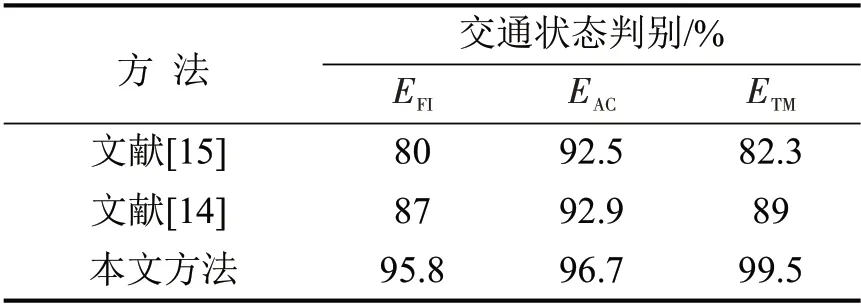
表2 交叉口交通状态识别比较Table2 Comparison of traffic state recognition at intersections

车辆的运动行为与交通状态关系密切，所提方法中速度、加速度等车辆运动参数作为图像化建模的关键指标并用以判别状态.因此，给出如图6所示的交叉口有效检测区域内车辆平均速度变化时交通状态的对应情况，图中以交叉口东西方向的交通状态为例，横坐标表示车辆排队长度，波纹为排队形成过程且用波纹灰度的深浅表示车速的高低，其中波纹越深表示车速越低.从图中可知，当交叉口有效检测区域内的车辆平均速度降低时，车辆的排队长度增长，交叉口的交通状态正由欠饱和状态向饱和，过饱和状态演变.

图6 不同速度下交叉口交通状态Fig.6 Traffic status of intersections at different speeds

4 结 论

从先进检测方式原始数据丰富特征入手，构建交叉口有效检测区域的图像化模型；将交叉口交通状态识别转化为图像搜索问题，利用监督哈希算法实现基于标签信息的图像搜索，得到交叉口的交通状态；最后，利用仿真采样数据对本文所提方法进行了验证.结果显示，所提方法可以精细识别交叉口时间序列上的全部交通状态.后续研究中，将在本文交通状态识别方法的基础上对交叉口的实时信号控制策略进行深入研究.

张立立，王力和赵琦3位作者对本文具有相同的贡献.