基于GMM-CHMM的城市道路换道行为识别

徐 婷，温常磊，张 香，李宝文，王 健，张亚坤

(1.长安大学汽车学院，西安710064；2.北京交通大学交通运输学院，北京100044)

0 引 言

不当换道行为导致交通事故屡见不鲜，造成惨重的人员伤亡及财产损失.美国高速公路安全管理局(NHTSA)调查数据显示：高达27%的交通事故由驾驶人换道引发[1]；我国由换道引发的交通事故约占4%～7%[2].因此，准确识别驾驶人换道行为对提高行车安全和降低交通事故发生率有非常重要的意义.

对于换道行为的研究，以不同角度的参数作为切入点，最常见的是环境参数和车辆参数，Yim等[3]将转向角等车辆运行状态数据作为模型输入，Schlechtriemen 等[4]将模型建立在与静态交通环境的关系上.研究换道行为的方法和模型也各有不同，有Logistic 回归模型[5]和支持向量机[6]等.有学者以驾驶人为研究对象，对驾驶人脑电图[7]、视觉特性[8]和头部特性[9]进行研究.

本文以降低城市道路换道事故率为目的，将城市道路换道行为作为研究对象，选取车载实时参数和前后车辆位置关系参数.车载实时参数有方向盘转角、转角方向、转向角速度、角速度方向、车速等；前后车辆位置关系参数有目标车辆与前方车辆相对距离、相对角度和相对速度.对参数进行统计学描述及独立样本T检验，确定将方向盘转角、转向角速度及本文定义的相对安全距离比作为表征城市道路驾驶人换道行为的特征参数，将3个参数的实时数据作为识别模型的观测矢量，识别模型混合了高斯混合模型(Gaussian Mixture Model，GMM)和连续型隐马尔可夫模型(Continuous Hidden Markov Model，CHMM)，识别模型能够准确地识别换道行为，最后对识别模型的性能进行了验证.

本文创新点在于同时采集了车载实时参数和车辆间相对位置参数，以安全距离为基础，将前后车辆间的干扰程度量化；方法上充分利用GMM对驾驶行为空间和时间上的连续性进行描述，可提高识别模型的识别准确率.

1 GMM-CHMM混合模型构建

驾驶行为具有强烈的时序性，连续型隐马尔可夫模型的最大特点是对时间序列敏感，能将前后时刻的状态相互联系起来.一个连续驾驶行为由时间序列微单元组成，观察序列由一系列的观测矢量组成.每个微单元都可能表现出不同的行为特征(换道行为或者车道保持行为特征)，这种行为特征是隐藏的，也就是隐马尔可夫模型中的隐藏状态.但是，可观测到的观察序列能间接表现出行为特征.

1.1 混合高斯模型

单多维高斯分布概率密度函数定义为

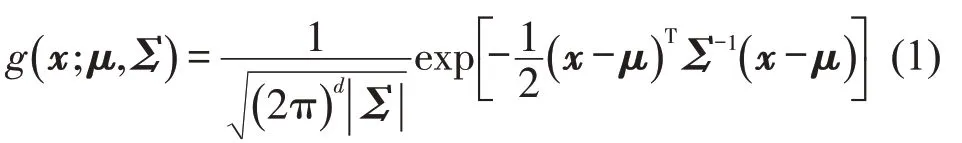
式中：x为多维数据样本；μ为样本均值；Σ为样本方差；d为数据维度.

混合高斯模型是由多个单高斯模型组成，定义为

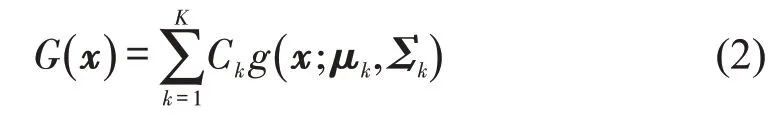
式中：K为单高斯模型个数；Ck为第k个单高斯模型的权值；μk，Σk为第k个单高斯模型中连续变量的均值矩阵和协方差矩阵.Ck，μk，Σk可以通过使用EM算法结合极大似然估计，以φ(i,k)为中间量求得.

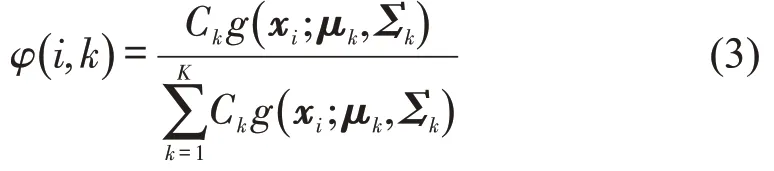
式中：φ(i,k)为第k个单高斯模型产生第i个观测矢量(方向盘转角，转向角速度等组成)的概率；xi为第i个观测矢量.

对数似然函数定义为

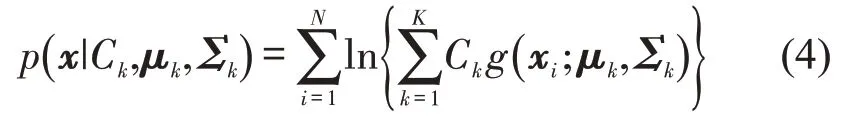
式中：p(x|Ck,μk,Σk)为混合高斯模型产生所有观测矢量x的最大概率值的对数；N为观测矢量数量.直到p(x|Ck,μk,Σk)收敛，最终求得Ck，μk，Σk.

1.2 连续型隐马尔可夫模型

连续型隐马尔可夫模型的一般形式为λ=[π,A,B] ，其中，π为初始状态概率分布，A为隐藏状态转移矩阵，B为混淆概率矩阵，在连续型隐马尔可夫模型中，B是由bj(Ot)组成的矩阵，j表示隐藏状态qj，t表示时刻，bj(Ot)为隐藏状态qj下观察到的观测向量为Ot的概率.

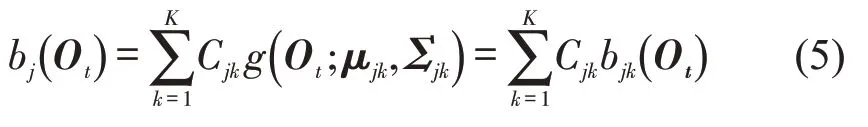
式中：Cjk，μjk，Σjk为隐藏状态qj(换道行为特征、车道保持行为特征)下，第k个单高斯模型的权值，均值矩阵及协方差矩阵；bjk(Ot)为隐藏状态qj下第k个单高斯模型观察到的观测向量为Ot的概率.

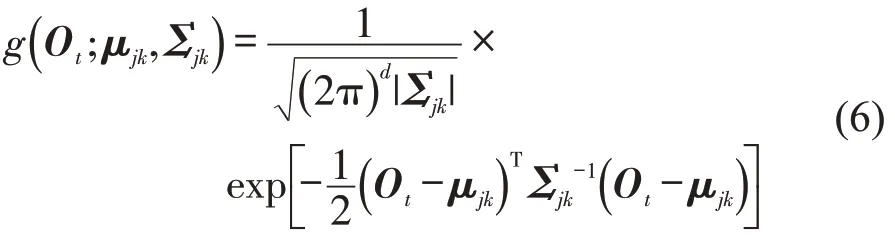
式中：π，A，C，μ，Σ可以通过将Baum-Welch算法和极大似然估计相结合，以γt(h)，ξt(h,j)为中间变量，迭代求得，γt(h)为t时刻隐藏状态为qh的概率；ξt(h,j)为t时刻隐藏状态为qh同时t+1时刻隐藏状态为qj的概率，C为由各个单高斯模型的权值组成的向量.

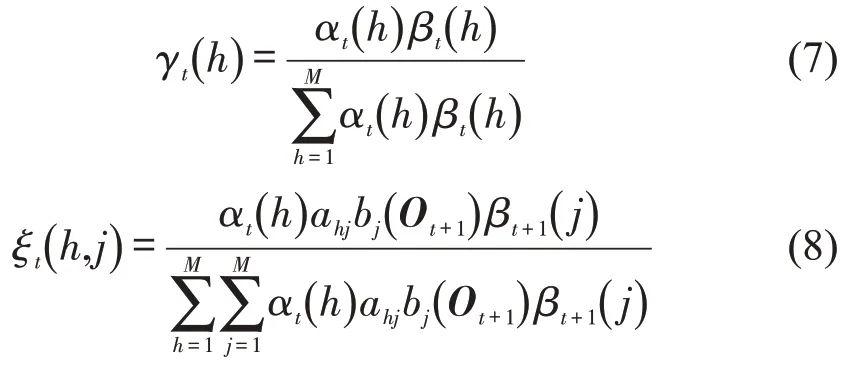
式中：αt(h)，βt(h)为t时刻的前向概率和后向概率；M为隐藏状态的数量；ahj为隐藏状态从qh转移为qj的概率.

直到似然函数p(O|λ)收敛.

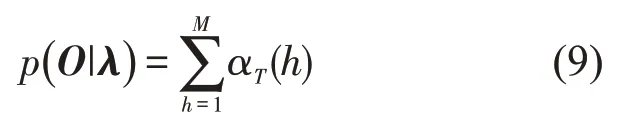
式中：p(O|λ)为换道行为识别模型λ产生观察序列O的最大似然概率；αT(h)为最终时刻T的前向概率.

2 数据采集和处理

2.1 数据采集

研究对象为城市道路驾驶人的换道行为，数据采集线路为西安市南二环路.西安市南二环路为西安城市快速干道，全长10.79 km，机动车行车道为双向6车道，每条车道宽3.5 m，设有中央分隔带，路宽50～100 m，设计速度为80 km/h，实验道路路况如图1所示.

表1为西安市南二环路主道交通流特性统计，数据采集自早高峰08：00，平峰13：00和晚高峰18：00.按照《公路工程技术标准JTG B01-2014》，轴距小于等于3.8 m为小型车，大于3.8 m为中、大型车.

由表1可知，小型车在城市道路交通组成中占比高达97%，为城市道路上最具代表的车型，又考虑到小客车和小货车具有相似的行驶特性，故本次实验车选择为小客车试验车.

实验用车型号是大众途安，车上装有车载自动诊断系统(OBD)、方向盘转角传感器、Delphi ESR 毫米波雷达和4个高清摄像头，用以采集车速(km/h)、方向盘转角(°)、制动开关、加速踏板开度、左右转向灯、转角方向、转向角速度(°/s)、角速度方向，与前方各个目标之间的相对距离(m)、相对角度(°)及相对速度(km/h)，共12个参数，同时采集实验车前方、后方、左侧和右侧的视频.

图1 前方和右侧视频Fig.1 Rear and right side video

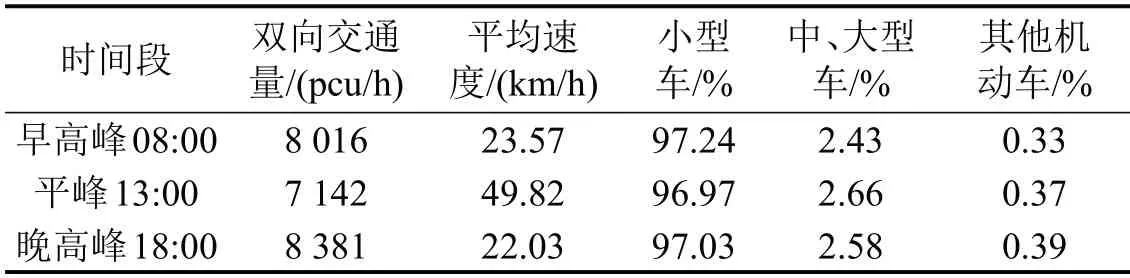
表1 西安市南二环主道交通流统计Table1 Traffic flow statistics of Nanerhuan main road

实验开始前，以自愿的方式招募18 位驾驶人参与，每位驾驶人均身体健康，年龄为27～40岁，驾龄为2～10年.本次道路实车实验在2017年10月23～30日进行，期间空气污染指数(API)小于100，天气晴朗，道路可见度良好，实验历时8 d，每位驾驶人进行4次道路实车实验，每次60 min，每1 s采集一次12条数据.

2.2 数据处理

定义δ为相对安全距离比，定量描述前后车辆间相对位置关系，δ与S成正比，与v成反比，关系式为

式中：S为前后车辆垂直相对距离；S0为前后车辆间安全距离.

当δ＜0 时，表示相对距离小于安全距离，两车会处于相对危险的状态；当δ≥0 时，两车在空间上会处于相对安全状态，但δ过大会导致道路在空间上的利用率降低.

式中：v为实验车(后车)速度；td为制动迟滞时间，td一般取1.2～2.0 s[10]；l为试验车停止后与正前方车辆的安全距离，一般取2～5 m[11].本文td和l均取均值，即td=1.6 s，l=3.5 m，得到

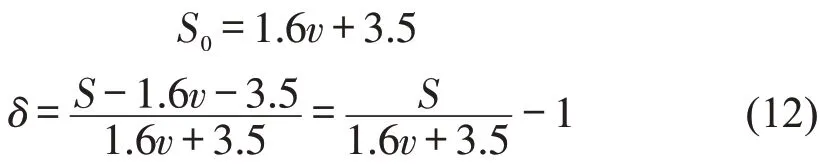
表2为对采集的部分原始数据的统计说明，该数据统计样本为一个持续时间为20 min的南二环道路实车驾驶过程(包括堵车过程)，共14 400条数据.表2显示了驾驶速度、方向盘转角和转向角速度的最大值、最小值、平均值和标准差，不同转角方向、不同角速度方向、不同制动开关状态和左右转向灯不同状态在样本中的占比，以及20 min 内加速踏板开度的平均值.

2.3 特征参数提取

分析高清摄像视频，将换道行为单元时间窗口确定为6 s，为消除时间窗口长度不同对统计分析的影响，将车道保持行为单元时间窗口也确定为6 s.最终，提取出412 个换道行为单元和824 个车道保持单元，共88 992条数据.对所有参数进行统计学分析和T 检验，表3和表4显示了θ,ω,δ在两个行为单元间有显著性差异.

从表3和表4可以分析得到：在换道行为单元中和车道保持行为单元中，θ,ω,δ的均值均存在显著性差异，且具有统计学意义.换道行为单元(LC)和车道保持行为单元(L-K)中的θ均值分别为7.62°和1.49°；ω均值分别为2.36°/s 和0.42°/s；δ均值分别为-0.248和-0.055，且δ小于0，说明在换道行为发生前后，前后车在位置上很紧密，前车对后车的干扰和影响较大.

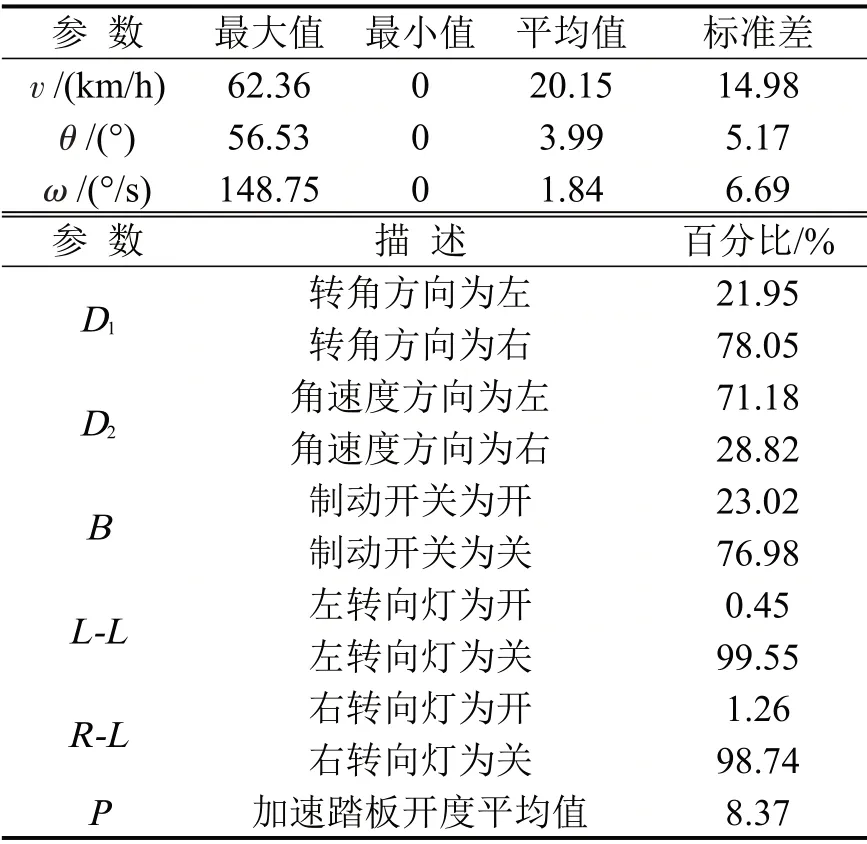
表2 数据统计说明Table2 Statistical interpretation of data

最终将方向盘转角θ、转向角速度ω及相对安全距离比δ作为换道行为特征参数.θ和ω是车载参数，δ是车辆前后位置参数，结合两种类型参数构建CHMM模型，可以提高模型的鲁棒性.

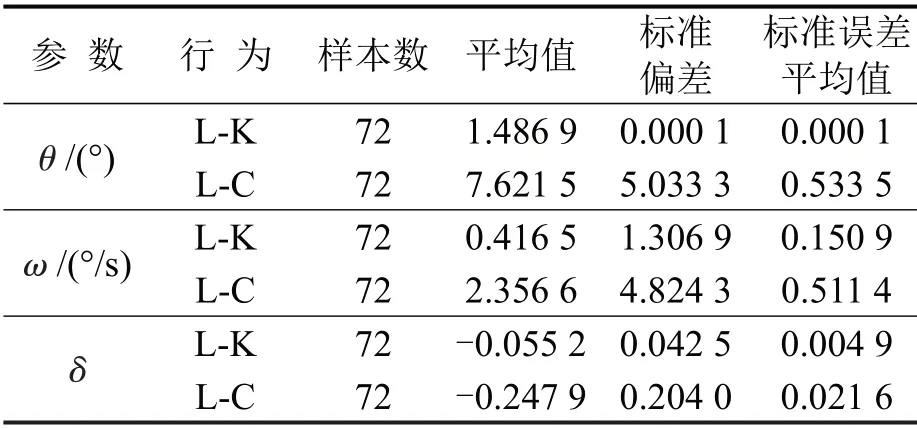
表3 特征参数统计学描述Table3 Statistical description of features parameters

3 换道行为识别混合模型

3.1 训练混合模型

识别模型由换道行为单元下的模型λC和车道保持(直线行驶)行为单元下的模型λK组成.

模型λC构建的具体步骤如下.

(1)假设一组初始参数λC=[π,A,C,μ,Σ]，π,C,μ,Σ一般用随机法取得.

(2)确定模型训练需要的样本，即观察序列Ot.

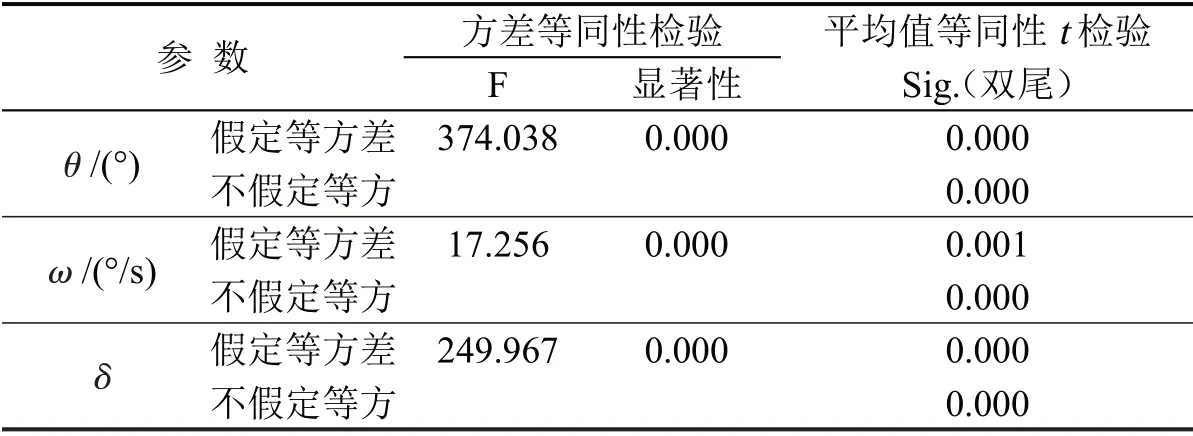
表4 两个不同行为单元间的独立样本检验Table4 Independent sample test between two different behaviors

参考Holdout 验证方法，总样本中的66%被随机选择作为训练样本，即共有272 个训练样本.部分训练样本如表5所示.

(3)在MATLAB 中编写程序，初始化参数π,A,C,μ,Σ后不断地迭代，直至Log-Likelihood收敛.

最终迭代到第18 次时，Log-Likelihood 收敛，结果如图2所示.

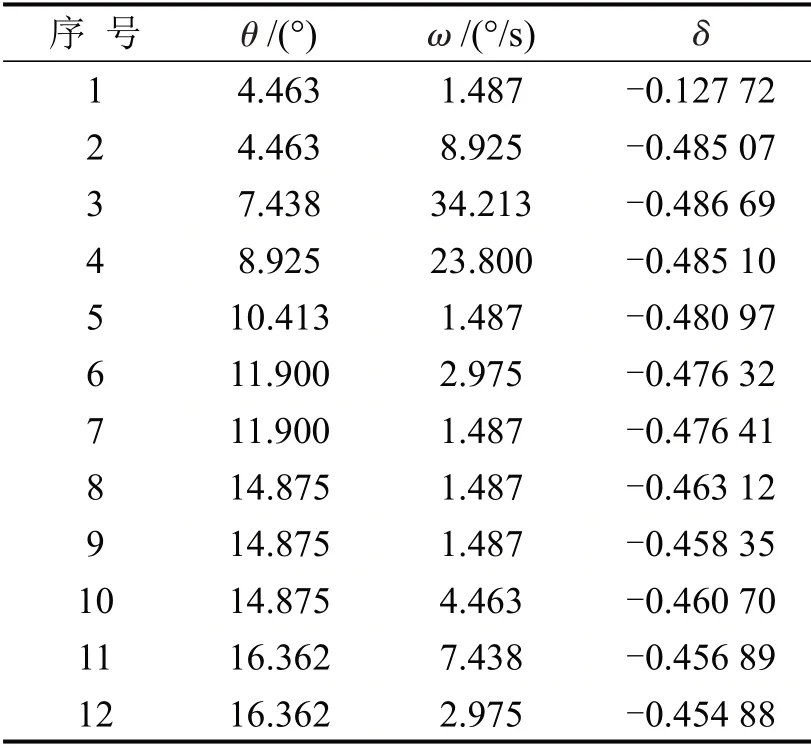
表5 换道训练样本Table5 Lane changing training sample

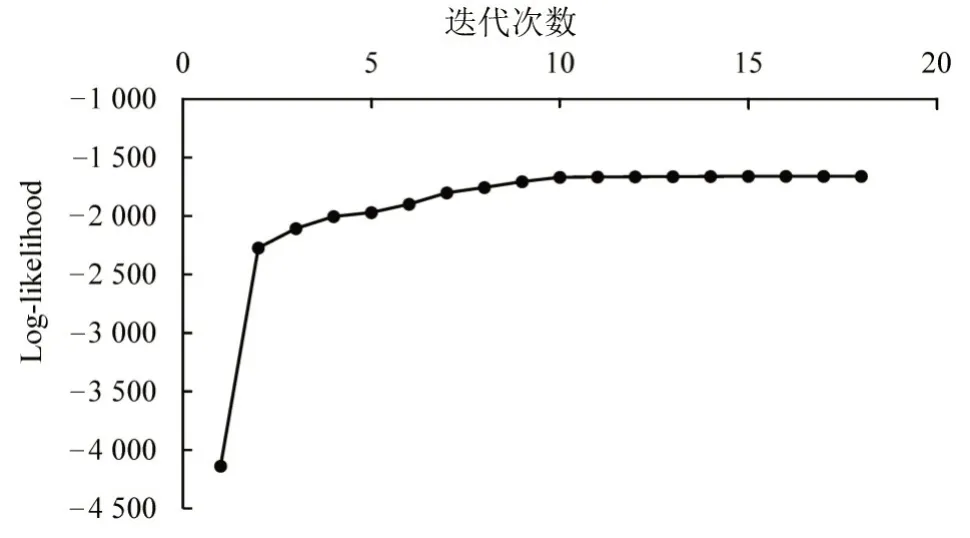
图2 迭代过程Fig.2 Iteration process

(4)模型结果.

模型λC的训练结果是一个由两个混合高斯模型组成的隐马尔可夫模型，其中每个混合高斯模型由3个3维高斯模型组成，最终的模型λC为

最终模型λC中：

①矩阵A中0.689 8 和0.310 2 是当前隐藏状态为换道特征，下一时刻隐藏状态为换道特征和车道保持特征的概率；0.268 5 和0.731 5 为当前隐藏状态为车道保持特征，下一时刻为换道特征和车道保持特征的转移概率.由转移概率的大小比较得到，驾驶行为隐藏状态在前后时刻的变化总是倾向于不变.

②矩阵C中的第一、二行表示微单元隐藏状态为换道特征下3 个子高斯模型的权值和车道保持特征下3 个子高斯模型的权值，分析可以得到，隐藏状态为车道保持特征下，第二个子高斯模型的权值明显大于其他两个，即观察矢量的分布主要由第二个子高斯模型决定.

③μ(：,：,m)的第一(二)列表示隐藏状态为换道特征(车道保持)下，第m个子高斯模型3 个变量(θ,ω,δ)的均值.从μ和C中分析得到，两个不同的隐藏状态下，θ，ω，δ的分布显著不同.

④Σ表示协方差矩阵，Σ(：,：,1,m)和Σ(：,：,2,m)分别表示换道特征和车道保持特征隐藏状态下，第m个子高斯模型3个变量之间的协方差矩阵.

3.2 模型检验

对需要识别的原始数据进行提取和处理，生成一组由一系列观测矢量组成的观察序列O，分别计算两个模型λC和λK生成这组观察序列的似然概率p(O|λC)和p(O|λK)，比较这两个概率，概率值大的，其对应模型就是数据表现出的驾驶人行为特征(换道行为特征或车道保持行为特征)，识别过程如图3所示.

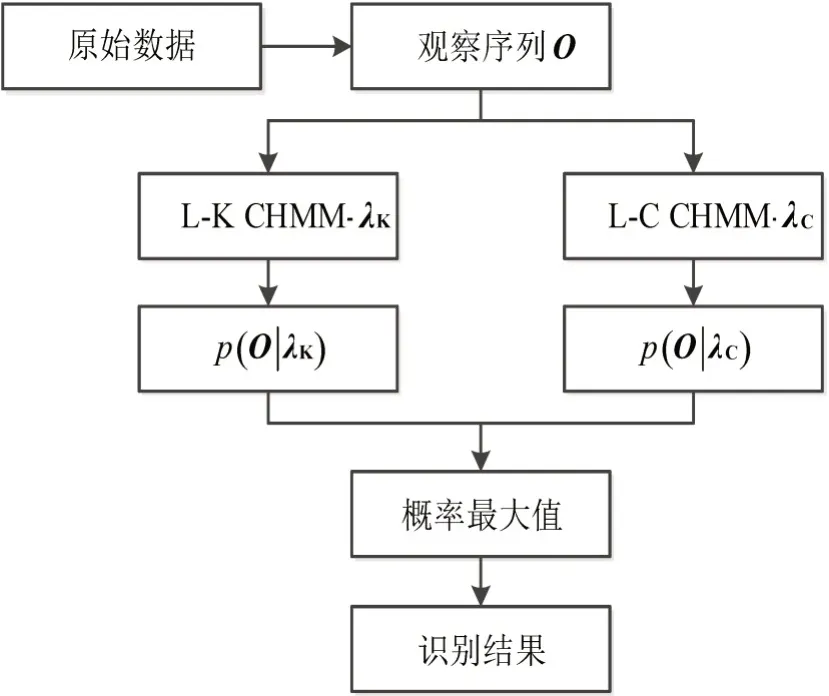
图3 换道行为识别过程Fig.3 Ddiagram of prediction

参考Holdout 验证方法，总样本中的34%被随机选择作为检验样本，即换道检验样本为140 个，车道保持检验样本为280个.由于似然概率太小不便比较，故对概率值取对数.部分结果如表6所示.

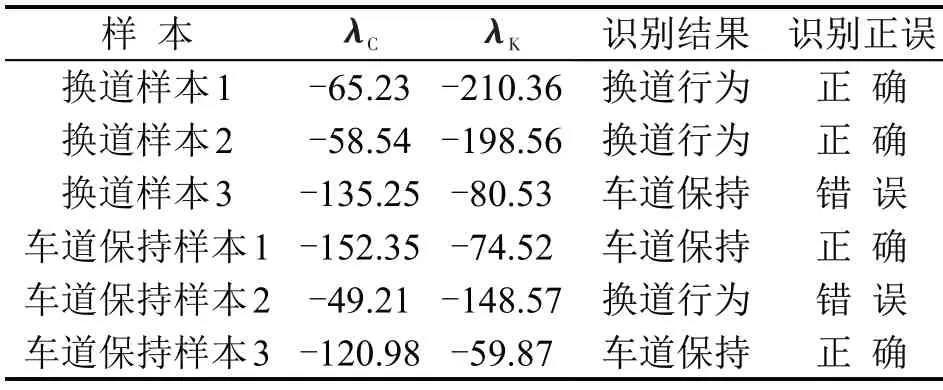
表6 识别结果Table6 Identification results

如表7所示，在140 个换道样本检验中，正确识别数量为131，换道行为识别精度达到93.6%，280个车道保持样本检验中，正确识别数量为253，车道保持识别精度达到90.4%，模型的性能良好.

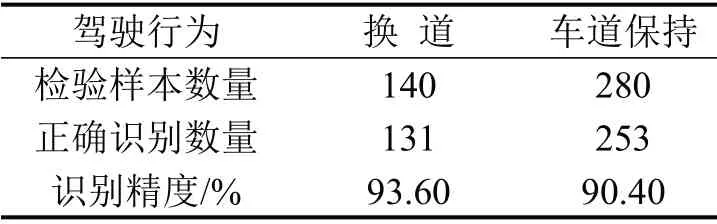
表7 识别精度Table7 Identification Accuracy

4 结 论

本文针对城市道路驾驶人换道行为，基于道路实车实验采集的车载实时数据，以及与前方车辆的相对角度、相对速度、相对距离等数据，构建了城市道路换道行为识别指标体系，提出了一种将混合高斯模型和连续型隐马尔可夫模型相结合的识别算法.为了使识别模型性能更加良好，本文通过定义参数相对安全距离比δ来定量描述前后车辆之间的相对位置关系及互相干扰程度，并且通过对提取出的数据进行统计学描述和独立样本T 检验，将3个连续变量，即方向盘转角θ，转向角速度ω及相对安全距离比δ确定为城市道路驾驶人换道行为识别体系的特征参数，最后对换道行为识别模型的性能进行检验，其中换道行为单元的识别精度高达93.6%，表明构建的GMM-CHMM模型性能良好.换道行为识别模型可以运用于高级驾驶辅助系统(ADAS)，对车辆的危险换道行为进行提前预警，也可应用到智能车领域，对智能车的自主换道过程进行优化，对提高车辆主动安全性有重要意义.将驾驶人、车辆及道路环境相结合，考虑更多的、不同方面的因素对换道行为的影响是未来的研究方向之一；超车行为可以视为两次更为复杂的连续换道行为，且不当的、频繁的超车行为也直接影响道路交通安全，因此对超车行为的识别和分析也是未来的研究方向之一.